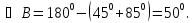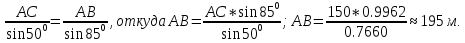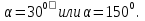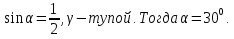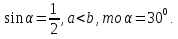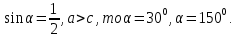Урок геометрии по теме: «Решение треугольников».

МАОУ ЛИЦЕЙ №44 г. Липецка

Учитель математики: Скорикова Людмила Алексеевна.

Урок геометрии по теме: «Решение треугольников».

Предмет: геометрия.

9 класс

Профиль: социально-экономический

Программа: базовый уровень

Тема: «Решение треугольников»

Цели урока:

1. Научить находить неизвестные элементы треугольника по известным углам и сторонам, т.е. по стороне и двум прилежащим углам, находить остальные стороны и угол;

2. Показать связь теории с практикой;

3. Способствовать выработке навыков решения задач, применяя теорему синусов.

4) Продолжить работу по развитию мыслительной деятельности - выделять главное, ставить и разрешать проблемы.

Задачи:

- актуализировать знание решения треугольников, развитие умения понимать сущность алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом.

- УУД:

Познавательные: овладение основами логического и алгоритмического мышления;

Интеллектуальные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;

Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;

Личностные: развитие умения ясно, точно, грамотно излагать свои мысли; понимать смысл поставленной задачи, развитие сотрудничества со сверстниками.

План урока

1. Сообщение темы и целей урока.

2. Вводная беседа.

3. Рассказ из истории и геометрии

4. Решение треугольника по стороне и двум прилежащим углам.

5. Решение задачи с практическим содержанием (нахождение расстояния до недоступной точки).

6. Подведение итогов урока.

Тип урока: урок изучения нового материала.

Ход урока.

1. Организационный момент.

Сообщение темы и целей урока и его девиза.

2. Мотивация урока.

.

Учитель начинает урок с того, что просит задуматься над тем, что в Кембриджском университете студентам часто напоминают следующее: «Если вы захотите поспать, то вам приснится ваша мечта. Если же вы окунетесь в учебу, то ваша мечта воплотится в жизнь». Пусть девизом сегодняшнего урока будут слова: «Окунемся в учебу, чтобы мечта воплотилась в жизнь».

Актуализация опорных знаний.

Тема «Решение треугольников» связана с решением прямоугольных треугольников, изучавшимся в VIII классе.

Теорема косинусов и теорема синусов, как обобщение теоремы Пифагора и соотношений между сторонами и синусами углов прямоугольного треугольника, позволяет решать любые треугольники по заданным тройкам элементов, их определяющим.

1. Теперь предстоит научить по данным длинам или градусным мерам трех элементов треугольника вычислять остальные его элементы, т.е. решать треугольники.

Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон его углов) по каким-нибудь трем данным.

Используют следующие обозначения:

Дан треугольник ABC.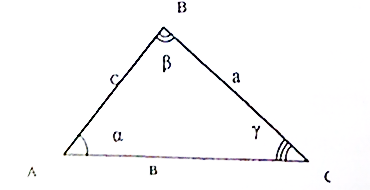

BC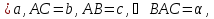

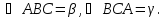
Выделены следующие задачи:

1. Дано:

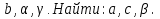
2. Дано: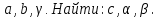

3. Дано: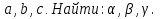

4. Дано: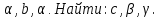

Решение этих задач основано на использовании теоремы синусов, теоремы косинусов, теоремы о сумме углов треугольника, следствии из теоремы синусов (в треугольнике против большого угла лежит большая сторона, против большей стороны лежит больший угол). И прежде чем приступить к решению различных задач, нам необходимо вспомнить

эти теоремы, которые применяются при решении треугольников. 1.Сформулируйте теорему синусов? Следствие из теоремы синусов? 2.Сформулируйте теорему косинусов?

3.Чему равна сумма углов треугольника? А знаете ли вы как можно это доказать только перегибанием треугольника?

2. Рассказ из истории геометрии. Зачем нужны эти задачи? В древней Греции наряду с блестящим развитием теоретической геометрии, научных методов исследования и логических доказательств большое значение имела прикладная геометрия. Римляне вообще занимались одной лишь практической и прикладной стороной математики, необходимой для землемерия, строительства городов, технических и военных вооружений.

Нить практической геометрии тянулась от вавилонян и древних египтян через Герона вплоть до новых времен. В итальянском учебнике XVIII в. есть иллюстрация, представленная ниже:

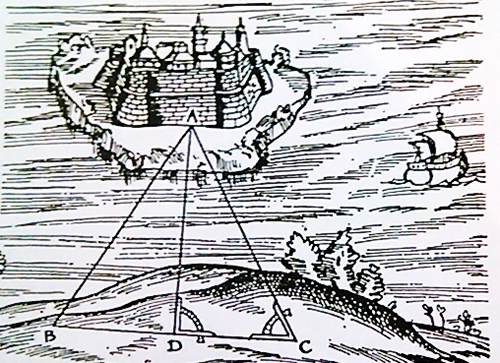
Измерение расстояния от берега до замка, расположенного Измерение расстояния от берега до замка, расположенного на острове.

Измерение расстояния от берега до замка, расположенного на острове.

В XVI-XVII вв. все более развивающаяся промышленность и торговля требует удовлетворения в первую очередь практических нужд. Появление первых инструментов и аппаратов для научных исследований (термометра, телескопа, барометра, микроскопа и др.) вызвало интерес среди широких кругов к практической стороне науки , и особенно к практической геометрии, которая нужна была для военных целей, мореплавания, строительства и землемерия. В этот период появляется много руководств по геометрии, в которых излагаются правила, формулы и рецепты для решения тех или иных практических задач.

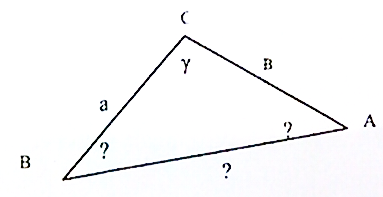
3. Наметим и запишем решение задачи 1.

Решение треугольника по стороне и двум углам.

Дано: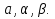

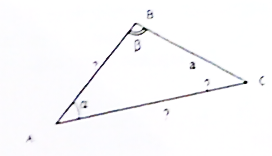
Найти: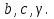

Решение:

1. 

2. ;

3. ;

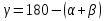
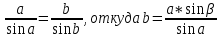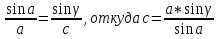Сколько решений может иметь задача?

Только одно, т.к. любые два треугольника, построенные по стороне и двум прилежащим углам будут равны.

4. Как найти расстояние до недоступного предмета (например, найти расстояние до цели)

Постановка проблемы.

Сами указываем размеры треугольника ABC.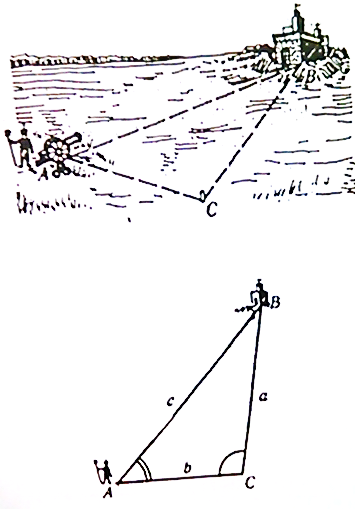

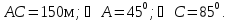
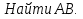
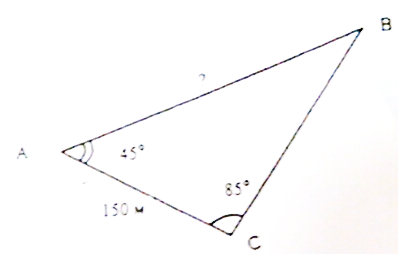
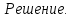
В этой задаче можно поставить и другой вопрос- из какой точки легче попасть в цель: из точки А или из точки С.

Для этого найдем СВ.

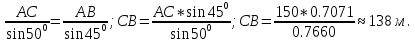
Все подсчеты производятся с помощью микрокалькулятора.

Задача № 26 (2) из учебника «Геометрия 7-9» А.В. Погорелов.

5. Подведение итогов, выставление оценок.

Домашнее задание: п. 112. № 26(3;4).

Рефлексивно-оценочная часть урока.

Обсуждение результатов работы.

Класс задумывается над оценкой своей работы по выполнению заданий на уроке.

Подведение итогов урока.

Вспоминаем основные моменты урока, анализируем усвоение предложенного материала и умение применить полученные знания в дальнейшем. Учащиеся отвечают на вопросы:

1. Что нового узнали на уроке?

2. Испытывали ли вы затруднения при решении задач?

3. Что было интересно?

4. Что у меня получилось?

5. Какие пробелы в знаниях выявились на уроке?

6. Какие проблемы у вас возникли по окончании урока?

Урок № 2

Тема: «Решение треугольников»

Цели урока:

1. Научить решать треугольник по двум сторонам и углу между ними;

2. Показать практическую направленность этой задачи;

3. Отрабатывать умение применять теорему синусов и косинусов в решении задач;

4. Вырабатывать внимание, активность, самостоятельность; продолжить работу по развитию мыслительной деятельности - выделять главное, ставить и разрешать проблемы, сравнивать и строить аналогии; работать над развитием речи - обогащать и усложнять ее словарный запас.

Задачи:

- актуализировать знание решения треугольников, развитие умения понимать сущность алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом.

- УУД:

Познавательные: овладение основами логического и алгоритмического мышления;

Интеллектуальные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;

Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;

Личностные: развитие умения ясно, точно, грамотно излагать свои мысли; понимать смысл поставленной задачи, развитие сотрудничества со сверстниками.

Тип урока: урок изучения нового материала.

План урока

1. Проверка домашнего задания.

2. Повторение.

3. Решение треугольника по двум сторонам и углу между ними.

4. Задача на движение.

5. Самостоятельная работа.

6. Итоги урока.

Ход урока.

2. Организационный момент.

Сообщение темы и целей урока и его девиза.

2. Мотивация урока.

Сегодня мы решим еще несколько задач на нахождение неизвестных элементов треугольника, попробуем свои силы для определения расстояния до недоступного примета. Мы попробуем свои силы, оценим свои знания, свои возможности в преодолении других трудностей. Этому и Фалес учил. Пусть его слова «Самое трудное - познать самого себя»(Фалес) и будут девизом этого урока.

Актуализация опорных знаний.

1. Два ученика у доски готовят решение домашней задачи № 26(3) и № 26(4)

2. С классом устно:

1. Повторить

2. 

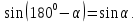
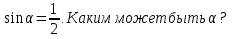
Разобрать различные случаи:

3. Решение треугольника по двум сторонам и углу между ними.

Постановка проблемы.

Дано:

Найти:

Решение.

Как

1.Как найти длину третьей стороны треугольника?

(С помощью теоремы косинусов).

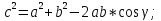
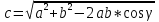
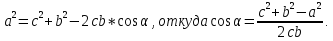
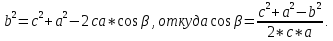
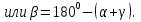
Как иначе можно найти углы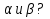

2 способ:

1. 

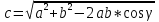
2. Если 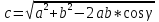- острый, то находим меньший из неизвестных, используя следствие из теоремы синусов (против большей стороны лежит больший угол).

Пусть a < b. Тогда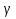

Находим острый угол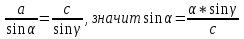

Выяснить, какой способ лучше?

Сколько решений имеет задача?

(Единственное решение, т.к. любые два треугольника с заданными сторонами и углу между ними будут равны).

Задача на движение.

Два парохода начинают свое движение одновременно из одного и того же пункта и двигаются равномерно по прямым , пересекающимся под углом . Скорость первого 70 км/ч, второго 60 км/ч. Вычислить на каком расстоянии друг от друга будут находится пароходы через 3 часа?

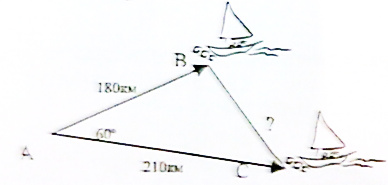
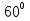
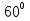
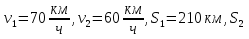
Давайте вычислим углы в образовавшемся треугольнике.

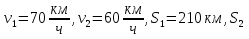
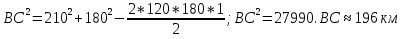
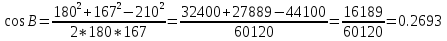
4. Самостоятельная работа