Разработки уроков: Решение неравенств второй степени с одной переменной (9 класс)

9класс Решение неравенств второй степени с одной переменной урок1

Цели: ввести понятие неравенства второй степени с одной переменной и изучить алгоритм решения таких неравенств.

Задачи: 1. Формировать умение решать неравенства второй степени с одной переменной.

2. развивать умения объяснять, строить логические цепочки решения уравнения, навыки решения целых уравнений, записывать, образное и логическое мышление, письменную и устную математическую речь

3. воспитывать аккуратность, ответственность, умение работать самостоятельно, интерес к изучению предмета.

Оборудование: учебник, доска, цветные мелки.

ХОД УРОКА

1. Организационный момент.

1. Проверка отсутствующих и готовности класса к уроку.

2.Сообщение темы и цели урока, запись на доске и в тетради

II. Устная работа.

1. Определите количество корней уравнения ах² + bx + c = 0 и знак коэффициента а, если на рисунке изображен график функции у = ах² ++ bx + c.

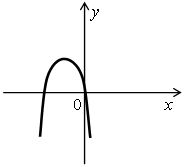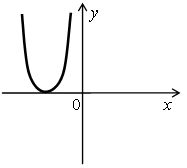а) б) в)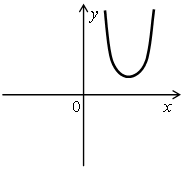

2. Назовите промежутки знакопостоянства функции у = ах² + bx + c, если ее график изображен на рисунке:

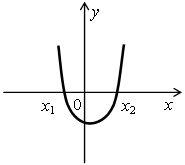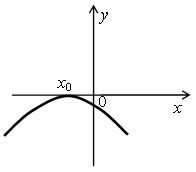а) б) в)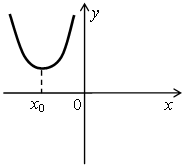

III. Объяснение нового материала.

1. В в е д е н и е п о н я т и я неравенства второй степени с одной переменной.

З а д а н и е. Какие из следующих неравенств являются неравенствами второй степени с одной переменной?

а) 2х² + 3х - 1 > 0; б) 4х² - х ≤ 0; в) 5х - 1 > 3х²;

г) 2х² - х + 1 < х⁴; д) х² ≥ 1; е) х² - 4x < .

2. С о с т а в л е н и е а л г о р и т м а решения неравенств второй степени с одной переменной.

Поставить перед учащимися проблему: как может быть решено неравенство подобного вида? Если учащиеся не догадаются, то можно вернуться к заданиям устной работы и наводящими вопросами помочь им сделать в ы в о д: неравенства второй степени с одной переменной решаются графически.

Желательно, чтобы учащиеся самостоятельно вывели алгоритм решения этих неравенств.

3. Р а с с м о т р е н и е п р и м е р о в решения неравенств второй степени с одной переменной.

IV. Формирование умений и навыков.

На этом уроке необходимо рассмотреть разные ситуации, возникающие при решении неравенств второй степени с одной переменной. Нужно, чтобы учащиеся запомнили алгоритм и применяли его без помощи учителя.

В соответствии с количеством корней трехчлена, получаемых в процессе решения неравенств, все задания можно разбить на три группы. В первую группу войдут неравенства, у которых квадратный трехчлен имеет два корня, во вторую - один корень, и в третьей группе будут неравенства, квадратный трехчлен которых не имеет корней.

№ 304 (а, в, ж) ученик у доски

№ 308 (а, в, д) ученик у доски

№ 304 (д).объясняет учитель

№ 318. Учитель с помощью учащихся

Р е ш е н и е. Пусть одна сторона прямоугольника равна а см, тогда другая сторона равна (а + 7) см. Значит, площадь прямоугольника равна а (а + 7) см², а по условию она не превосходит 60 см². Получим неравенство: а (а + 7) ≤ 60; а (а + 7) - 60 ≤ 0.

Решая его, находим, что а [-12; 5], то есть меньшая сторона прямоугольника не должна превосходить 5 см.

О т в е т: не превосходит 5 см.

ФМ для снятия утомления с плечевого пояса и рук

1. И.п. - о.с. 1 - поднять плечи. 2 - опустить плечи. Повторить 6-8 раз, затем пауза 2-3 с, расслабить мышцы плечевого пояса. Темп медленный.

2. И.п. - руки согнуты перед грудью. 1 - 2 - два пружинящих рывка назад согнутыми руками. 3 - 4 - то же прямыми руками. Повторить 4-6 раз. Темп средний.

3. И.п. - стойка ноги врозь. 1 - 4 - четыре последовательных круга руками назад. 5 - 8 - то же вперед. Руки не напрягать, туловище не поворачивать. Повторить 4-6 раз. Закончить расслаблением. Темп средний.

Д о п о л н и т е л ь н ы е з а д а н и я.

1. № 379.

Р е ш е н и е. (а + 2) х² + 8х + а - 4 = 0.

Чтобы данное уравнение имело 2 решения, необходимо выполнение следующих условий:

- уравнение должно быть квадратным, то есть а + 2 ≠ 0;

- дискриминант этого квадратного уравнения должен быть положителен.

Согласно этим условиям получим систему:

Решением второго неравенства системы является промежуток (-6; 4). С учетом того, что а ≠ -2, получим: а (-6; -2) (-2; 4).

О т в е т: (-6; -2) (-2; 4).

2. При каких значениях параметра а неравенство ах² + 2ах + 4 > 0 выполняется на всей числовой оси?

Р е ш е н и е. Чтобы данное неравенство выполнялось на всей числовой оси, необходимо, чтобы ветви параболы были направлены вверх, и квадратный трехчлен не имел корней, то есть D₁ = а² - 4а < 0.

Решая это неравенство, получим, что а (0; 4). Этот промежуток удовлетворяет обоим условиям. Однако нужно рассмотреть еще случай, когда а = 0. Подставляя это значение в исходное неравенство, получим: 4 > 0.

Это неравенство верно, поэтому при а = 0 исходное неравенство будет выполняться на всей числовой оси.

О т в е т: [0; 4).

V. Итоги урока.

- Какие неравенства называются неравенствами второй степени с одной переменной?

- Опишите алгоритм решения неравенств второй степени с одной переменной.

- Какие решения может иметь неравенство второй степени с одной переменной, если соответствующий квадратный трехчлен не имеет корней?

Рефлексия:

1) Что вызывало у вас затруднения в начале урока и что стало понятно в течение урока?

2) Какие моменты урока особенно понравились? Когда вам было неуютно? Почему?

• Общая характеристика знаний учащихся, определение положительных и отрицательных моментов.

• Сообщение оценок учащимся

Домашнее задание: № 304 (б, з), № 306 (в), № 308 (г).

9класс Решение неравенств второй степени с одной переменной урок2

Цель: продолжить формирование умения решать неравенства второй степени с одной переменной.

Задачи: 1. учить решать неравенства второй степени с одной переменной

2. развивать умения объяснять, строить логические цепочки решения уравнения, навыки решения целых уравнений, записывать, образное и логическое мышление, письменную и устную математическую речь

3. воспитывать аккуратность, ответственность, умение работать самостоятельно, интерес к изучению предмета.

Оборудование: учебник, доска, цветные мелки.

ХОД УРОКА

2. Организационный момент.

1. Проверка отсутствующих и готовности класса к уроку.

2.Сообщение темы и цели урока, запись на доске и в тетради

II. Устная работа.

Решите неравенства ах² + bx + c > 0 и ах² + bx + c ≤ 0, если на рисунке изображен график соответствующей квадратичной функции:

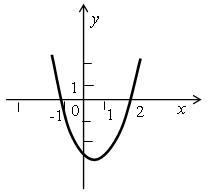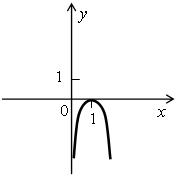а) б) в)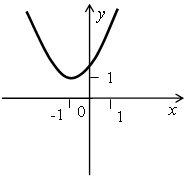

III. Формирование умений и навыков.

1. № 307, № 309 (а, в, д).

2. № 312 (а, в).

3. № 315 (в).

4. № 316 (4).

№ 320 (а). Р е ш е н и е

а)

Найдем корни квадратных трехчленов и изобразим схематически параболы на одной числовой прямой:

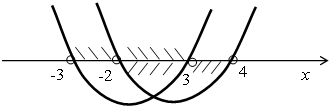
По рисунку видим, что решением данной системы будет промежуток (-2; 3).

О т в е т: (-2; 3).

2. № 321 (а).

Р е ш е н и е

Для нахождения области определения данной функции достаточно решить систему неравенств:

Так же, как в предыдущем задании, наносим на числовую прямую параболы и заштриховываем искомые промежутки:

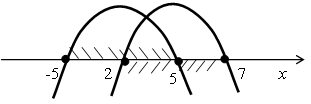
Получаем, что х [2; 5]. О т в е т: 2; 3; 4; 5.

IV. Математический диктант.

«+» - согласен с утверждением; «-» - не согласен с утверждением.

1) Неравенства второй степени с одной переменной решаются с помощью графика квадратичной функции.

2) Для решения неравенств второй степени с одной переменной нужно знать координату вершины соответствующей параболы.

3) Для решения неравенств второй степени с одной переменной достаточно знать направление ветвей соответствующей параболы.

4) Если квадратный трехчлен имеет корни, то соответствующее неравенство обязательно имеет решения.

5) Если квадратный трехчлен не имеет корней, то соответствующее неравенство не имеет решений.

6) Если вершина параболы лежит на оси абсцисс, то соответствующее неравенство не имеет решений.

7) Неравенства второй степени с одной переменной может иметь решение, состоящее из единственного числа.

8) Решением неравенства второй степени с одной переменной может быть множество всех чисел.

9) Если а < 0, х₁ и х₂ - корни квадратного трехчлена ах² + bx + c, то решением неравенства ах² + bx + c > 0 будет промежуток (-∞; х₁) (х₂; +∞).

10) Если а > 0 и х₀ - единственный корень квадратного трехчлена ах² + bx + c, то решением неравенства ах² + bx + c > 0 будет промежуток (-∞; х₀)(х₀; +∞).

К л ю ч: + - - + - - + + - +.

Учащиеся обмениваются тетрадями, учитель вновь зачитывает вопросы математического диктанта. Происходит обсуждение ответов и учащиеся выставляют друг другу оценки по следующей шкале:

«5» - не менее 9 правильных ответов;

«4» - 7, 8 правильных ответов;

«3» - 5, 6 правильных ответов;

«2» - менее 5 правильных ответов.

3. При каких значениях т область определения функции

f (х) = состоит из одной точки?

Р е ш е н и е

Чтобы найти область определения данной функции, нужно решить систему неравенств:

Эта система будет иметь единственное решение в двух случаях:

- если квадратный трехчлен х² -2тх + 5 будет иметь единственный корень, не превосходящий 1: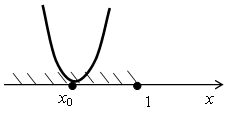

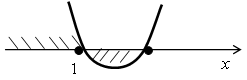
- если квадратный трехчлен х² -2тх + 5 будет иметь два корня, меньший из которых равен 1:

Первое условие будет выполнено, если дискриминант квадратного трехчлена х² - 2тх + 5 равен нулю, а корень

х₀ = ≤ 1. Имеем: D₁ = т² - 5; х₀ = = m.

Получим систему:

Ее решением является m = -.

Второе условие будет выполнено, если f (1) = 0, то есть 1 - 2т + 5 = 0, откуда т = 3. Подставляя это значение т, получим трехчлен х² - 6х + 5; вторым его корнем будет число 5. Значит, т = 3 удовлетворяет условию задачи.

О т в е т: -; 3.

Физкультминутка общего воздействия

1. И.п. - стойка ноги врозь. 1 - руки назад. 2-3 - руки в стороны и вверх, встать на носки. 4 - расслабляя плечевой пояс, руки вниз с небольшим наклоном вперед. Повторить 4-6 раз. Темп медленный.

2. И.п. - стойка ноги врозь, руки согнутые вперед, кисти, в кулаках, 1-е поворотом туловища налево удар правой рукой вперед. 2 - и.п. 3-4 - то же в другую сторону. Повторить 6-8 раз. Дыхание не задерживать.

3. И.п. - о.с. 1 - хлопок в ладоши за спиной, руки поднять назад возможно выше. 2 - движение рук через стороны, хлопок в ладоши вперед на уровне головы. Повторить 4-6 раз. Темп быстрый.

4. И.п. - сидя на стуле. 1 - голову наклонить вправо. 2 - и.п. 3 - голову наклонить влево. 4 - и.п. Повторить 4-6 раз. Темп средний.

V. Проверочная работа.

В а р и а н т 1

Решите неравенство:

а) х² - 8х + 15 > 0; в) 4х² + 4х + 1 ≤ 0;

б) 2х - х² ≥ 0; г) х² + 2х + 3 > 0.

В а р и а н т 2

Решите неравенство:

а) х² - 10х + 21 ≤ 0; в) х² - 10х + 25 > 0;

б) 9 - х² < 0; г) -х² + х - 4 ≤ 0.

V II. Итоги урока.

- Опишите алгоритм решения неравенств второй степени с одной переменной.

- Когда решение неравенства второй степени с одной переменной будет состоять из единственного числа? из бесконечного множества чисел?

- Какие решения может иметь неравенство ах² + bx + c > 0, если

а) а > 0 и х₁, х₂ - корни квадратного трехчлена ах² + bx + c;

б) а < 0 и квадратный трехчлен имеет единственный корень х₀;

в) а > 0 и квадратный трехчлен ах² + bx + c не имеет корней?

Рефлексия:

1) Что вызывало у вас затруднения в начале урока и что стало понятно в течение урока?

2) Какие моменты урока особенно понравились? Когда вам было неуютно? Почему?

• Общая характеристика знаний учащихся, определение положительных и отрицательных моментов.

• Сообщение оценок учащимся

Домашнее задание: № 309 (г, е), № 313, № 317.

Факультативное занятие

Более сложные задачи, требующие применения
алгоритма решения неравенств второй степени
с одной переменной

Цели: продолжить формирование умения применять алгоритм решения неравенств второй степени с одной переменной.

Ход урока

I. Организационный момент.

II. Устная работа.

Решите неравенство ах² + bx + c ≤ 0 и ах² + bx + c > 0, если на рисунке изображен график соответствующей квадратичной функции:

а) 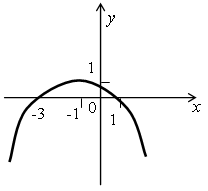б)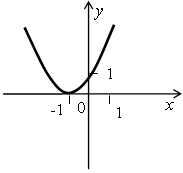

в)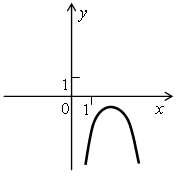

III. Проверочная работа.

В а р и а н т 1

Решите неравенство:

а) х² - 8х + 15 > 0; в) 4х² + 4х + 1 ≤ 0;

б) 2х - х² ≥ 0; г) х² + 2х + 3 > 0.

В а р и а н т 2

Решите неравенство:

а) х² - 10х + 21 ≤ 0; в) х² - 10х + 25 > 0;

б) 9 - х² < 0; г) -х² + х - 4 ≤ 0.

IV. Формирование умений и навыков.

На этом уроке учащиеся должны решать более сложные задания, которые потребуют от них осознанного владения алгоритмом решения неравенств второй степени с одной переменной.

Все задания можно разбить на 2 группы. Если класс невысокого уровня подготовки, то вторую группу заданий решать не нужно. Кроме того, сильным в учебе учащимся можно дать дополнительные задания на решение уравнений и неравенств с параметрами.

Упражнения:

1-я г р у п п а.

1. № 310 (а), № 311 (а).

2. № 314 (а).

3. № 318.

Р е ш е н и е

Пусть одна сторона прямоугольника равна а см, тогда другая сторона равна (а + 7) см. Значит, площадь прямоугольника равна а (а + 7) см², а по условию она не превосходит 60 см². Получим неравенство:

а (а + 7) ≤ 60;

а (а + 7) - 60 ≤ 0.

Решая его, находим, что а [-12; 5], то есть меньшая сторона прямоугольника не должна превосходить 5 см.

О т в е т: не превосходит 5 см.

2-я г р у п п а.

1. № 320 (а, в, д).

Р е ш е н и е

а)

Найдем корни квадратных трехчленов и изобразим схематически параболы на одной числовой прямой:

По рисунку видим, что решением данной системы будет промежуток (-2; 3).

О т в е т: (-2; 3).

2. № 321 (а).

Р е ш е н и е

Для нахождения области определения данной функции достаточно решить систему неравенств:

Так же, как в предыдущем задании, наносим на числовую прямую параболы и заштриховываем искомые промежутки:

Получаем, что х [2; 5].

О т в е т: 2; 3; 4; 5.

Д о п о л н и т е л ь н ы е з а д а н и я.

1. № 379.

Р е ш е н и е

(а + 2) х² + 8х + а - 4 = 0.

Чтобы данное уравнение имело 2 решения, необходимо выполнение следующих условий:

- уравнение должно быть квадратным, то есть а + 2 ≠ 0;

- дискриминант этого квадратного уравнения должен быть положителен.

Согласно этим условиям получим систему:

Решением второго неравенства системы является промежуток (-6; 4). С учетом того, что а ≠ -2, получим: а (-6; -2) (-2; 4).

О т в е т: (-6; -2) (-2; 4).

2. При каких значениях параметра а неравенство ах² + 2ах + 4 > 0 выполняется на всей числовой оси?

Р е ш е н и е

Чтобы данное неравенство выполнялось на всей числовой оси, необходимо, чтобы ветви параболы были направлены вверх, и квадратный трехчлен не имел корней, то есть D₁ = а² - 4а < 0.

Решая это неравенство, получим, что а (0; 4). Этот промежуток удовлетворяет обоим условиям. Однако нужно рассмотреть еще случай, когда а = 0. Подставляя это значение в исходное неравенство, получим: 4 > 0.

Это неравенство верно, поэтому при а = 0 исходное неравенство будет выполняться на всей числовой оси.

О т в е т: [0; 4).

3. При каких значениях т область определения функции

f (х) = состоит из одной точки?

Р е ш е н и е

Чтобы найти область определения данной функции, нужно решить систему неравенств:

Эта система будет иметь единственное решение в двух случаях:

- если квадратный трехчлен х² -2тх + 5 будет иметь единственный корень, не превосходящий 1:

- если квадратный трехчлен х² -2тх + 5 будет иметь два корня, меньший из которых равен 1:

Первое условие будет выполнено, если дискриминант квадратного трехчлена х² - 2тх + 5 равен нулю, а корень

х₀ = ≤ 1. Имеем:

D₁ = т² - 5;

х₀ = = m.

Получим систему:

Ее решением является m = -.

Второе условие будет выполнено, если f (1) = 0, то есть 1 - 2т + 5 = 0, откуда т = 3. Подставляя это значение т, получим трехчлен х² - 6х + 5; вторым его корнем будет число 5. Значит, т = 3 удовлетворяет условию задачи.

О т в е т: -; 3.

V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

- Опишите алгоритм решения неравенств второй степени с одной переменной.

- Когда решение неравенства второй степени с одной переменной будет состоять из единственного числа? из бесконечного множества чисел?

- Какие решения может иметь неравенство ах² + bx + c > 0, если

а) а > 0 и х₁, х₂ - корни квадратного трехчлена ах² + bx + c;

б) а < 0 и квадратный трехчлен имеет единственный корень х₀;

в) а > 0 и квадратный трехчлен ах² + bx + c не имеет корней?

Домашнее задание: № 311 (б), № 314 (б), № 319, № 320 (б, г, е).

Д о п о л н и т е л ь н о: № 321 (б), № 380.