Конспект занятия-практикума по теме «Задачи, содержащие параметры и модули». 11 класс.

Муниципальное бюджетное образовательное учреждение

средняя общеобразовательная школа № 6.

Занятие-практикум по теме

«Задачи, содержащие параметры

и модули».

11 класс .

Учитель: Гордиенко Зоя Николаевна.

Занятие-практикум по теме «Задачи , содержащие параметры и модули».

Замечание .Занятие проводится с группой учащихся из 9 человек с достаточно высоким уровнем математической подготовки.

Цель занятия:

-Обобщить понятия параметра и модуля и включить эти понятия в систему решения нестандартных задач;

-обобщить и закрепить свойства функций с модулем и с их помощью освоить геометрические приемы решения нестандартных уравнений.

Задачи :

-повторить алгоритм построения графиков функций, содержащих модули;

-построить графики различных линейных и квадратичных функций, содержащих модули и с их помощью решить уравнения с параметрами;

-показать учащимся аналитический способ решения уравнений с модулем, содержащих параметр как альтернативный графическому.

Оборудование :

• плакаты с графиками к заданиям №1………

• индивидуальный раздаточный материал.

Ход занятия:

1. Организационный момент.

2. Проверка домашнего задания:

Домашнее задание

№1.Решить уравнение|1-x|=2-|x| двумя способами:

• аналитически;

• графически.

Проверка ответов: х=-0,5; х=1,5

-Какой способ легче?(различные аргументированные ответы учащихся).

№2.Построить графики функций:

1. у=|x+3|-2; -есть ли вопросы по построению этих графиков?

2. y=|

3. y= -проверяем; график данной функции на ватмане крепится на магнитную доску.

3.Решение задач. Включение ранее изученного материала в систему знаний с целью решения нестандартных задач повышенного уровня сложности .

-Какую смысловую нагрузку в уравнении несет параметр?

(От его значений зависит количество решений уравнения: меняется значение параметра-

получаем новое решение уравнения или доказываем , что решений нет).

-Правильно,- решить уравнение с параметром- значит указать , при каких значениях параметров существуют решения и каковы они:

• определить множество допустимых значений неизвестного и параметра;

• для каждого допустимого значения параметра найти соответствующее решение(или решения) уравнения.

-Решая задание №1 из домашней работы, мы обратили внимание, что графический способ решения уравнений иногда бывает более легким и понятным. Сейчас мы вместе рассмотрим задание, которое было в КИМах ЕГЭ в 2011году.

Задание№1. 1.Найдите все значения a,при которых график функции f(x)=+ пересекает ось абсцисс:

а) в одной точке;

б) в двух точках;

в) в трех точках.

/ Задание рассматривается учителем с привлечением учащихся по ходу решения задачи/

Ход решения:

1. вспомогательная функция y=g(x) , где g(x)=;

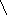график функции у = пересекает ось х при условиях, указанных в задании, если уравнение g(x)=a имеет 1;2 и более решений.

g(x)=;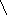

нули модуля:-3;1 + -3 - 1 +

х

(- g(x)=-2x +3;

g(x)=2+2x -3;

Таблица с графиком вспомогательной функции крепится на магнитную доску.

табл.1

y=a-горизонтальная прямая, параллельная оси х;

а)если а , т.е. а-одно решение( точка)

а-одно решение( точка)

б)если а=-3,5 и а=1 -два решения;

в) -3,5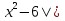-более двух решений (3 точки)

Далее к доске приглашаются 2 человека для решения заданий № 2 и №3. Задания ре-

шаются графически, затем рассматривается аналитический способ решения; в

задании №2 решение выполняется учителем с участием в решении учащихся, № 3 решается учеником в сопровождении учителя.

№2 Найдите все значения a при каждом из которых уравнение 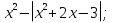имеет ровно три корня .Если значений a окажется несколько, то в ответе запишите их сумму .

у=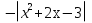-вспомогательная функция

.

при а=2 -ровно 3 корня

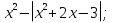а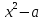-условие существования модуля.

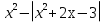
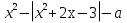
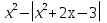
-2;2-нули модулей; а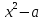 определим количество корней совокупности:

0к 2к+2к

1. 2

2 корня 2корня+1корень 2корня+0корней

№3.Найдите все значения a,при которых уравнение 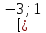имеет ровно три корня .Если значений a окажется несколько, то в ответе запишите их сумму.

ровно 3 корня, если а+1=4,т.е. а=3

=

;;

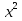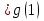
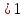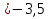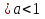
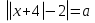
-5 -1 2к+2к 3 2к+0к

(1)и(2)совп

2к 2к+1к

№4. Найдите все значения a,при каждом из которых уравнение 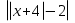имеет ровно один корень .Если значений a окажется несколько, то в ответе укажите их сумму.

Ученик решает задание аналитическим способом.

0к+0к -17 2к+0к 5 2к+2к

1к+0к 2к+1к

а=5; а=-17 -нули модулей

|x|-a-6=11; |x|=17+a; приа=-17- единственный корень.

|x|-a-6=-11; |x|=-5+a.

№ 5. Найдите все значения параметра a при котором уравнение 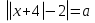имеет

бесконечное множество решений. Если таких значений несколько, то в ответе укажите их сумму.

(Учащиеся самостоятельно строят график вспомогательной функции, затем осуществляется самоконтроль с помощью табл.2, которая крепится на магнитной доске)

Табл.2

бесконечное множество решений при а=7 и а=-7;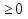

За 7мин до конца занятия проверочная работа: один ученик на закрытой доске, остальные на местах, затем проверка решения.

Домашнее задание:№10,11,12

Раздаточный материал для учащихся для работы на занятии и домашней работы.

1.Найдите все значения a,при которых график функции f(x)=+ пересекает ось абсцисс:

а) в одной точке;

б) в двух точках;

в) в трех точках.

2. Найдите все значения a при каждом из которых уравнение 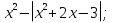имеет ровно три корня .Если значений a окажется несколько, то в ответе запишите их сумму.

3. Найдите все значения a,при которых уравнение 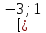имеет ровно три корня .Если значений a окажется несколько, то в ответе запишите их сумму.

4. Найдите все значения a,при каждом из которых уравнение 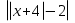имеет ровно один корень .Если значений a окажется несколько, то в ответе укажите их сумму.

5. Найдите все значения параметра a при котором уравнение 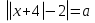имеет

бесконечное множество решений. Если таких значений несколько, то в ответе укажите их сумму.

6.Найдите наименьшее значение параметра a , при котором уравнение

a-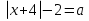 будет иметь ровно 2 решения.

7. Найдите все значения a,при каждом из которых уравнение x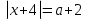 имеет ровно 2 различных корня. Если таких значений более одного, то в ответе укажите их сумму.

8.Найдите все значения a,при каждом из которых уравнение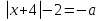

если таких значений более одного, то в ответе напишите наибольшее значение.

9. Найдите все значения a,при каждом из которых уравнение 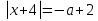имеет ровно 3 корня.

Задания для работы дома

10. Найдите все значения a при каждом из которых уравнение 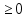имеет ровно три корня .Если значений a окажется несколько, то в ответе запишите их сумму.

11. Найдите все значения a,при которых уравнение 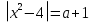имеет ровно три корня .Если значений a окажется несколько, то в ответе запишите их сумму.

12. . Найдите все значения a, при каждом из которых график функции

f(x)=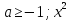 пересекает ось абсцисс менее чем в трех различных

точках.

табл.1

табл.2