- Учителю
- Урок по алгебре «Формулы сложения» (9 класс)
Урок по алгебре «Формулы сложения» (9 класс)
Урок № 34
Тема урока: «Формулы сложения»
Цель урока: познакомиться с формулами суммы и разности двух углов, научитесь применять эти формулы в тождественных преобразованиях тригонометрических выражений, развить познавательный интерес, продолжить формирование математической культуры.
ХОД УРОКА:
1.Организационный момент.
Приветствие учащихся. Постановка цели урока.
2. Объяснение нового материала
Определение: Формулами сложения называются формулы, позволяющие выразить тригонометрические функции суммы и разности двух углов через тригонометрические функции этих же углов.
Вначале дадим вывод формулы косинуса разности двух углов через тригонометрические функции тех же углов. Для этой цели, как обычно, рассматриваем окружность с центром, расположенным в начале прямоугольной системы координат и радиусом R = OA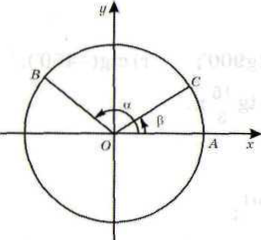
Начальный радиус OA повернем вокруг точки О на углы α и β. В результате получим соответствующие радиусы ОВ и ОС. Из курса геометрии вам известно, что если точка В имеет координаты xt и у., а точка С - координаты х2 и у2, то векторы 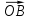 и
и 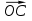 также имеют соответственно те же координаты, т.е.
также имеют соответственно те же координаты, т.е. 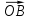 (xt;у,) и
(xt;у,) и 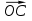 (х2; у.,).
(х2; у.,).
Теперь найдем скалярное произведение векторов ОВ и ОС. Из курса геометрии известно, что скалярное произведение этих двух векторов определяется равенством
![]() (1)
(1)
По определению косинуса и синуса углов α и β мы имеем:
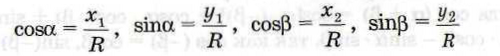
ИЛИ
![]()
Подставив эти значения в равенство (1), имеем:
![]()
Итак,
![]()
Левую часть равенства (2) запишем в следующем виде, используя теорему о скалярном произведении двух векторов:
![]()
Угол между векторами 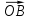 и
и 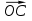 есть угол ВОС или угол, равный α - β (рис.2). Но в общем виде угол ВОС между векторами
есть угол ВОС или угол, равный α - β (рис.2). Но в общем виде угол ВОС между векторами 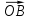 и
и 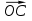 может быть равным 2π - (α - β) или от них может отличаться на кратное число полного угла
может быть равным 2π - (α - β) или от них может отличаться на кратное число полного угла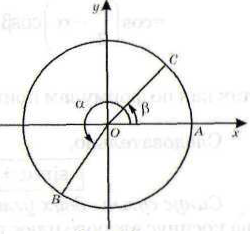
Поэтому во всех случаях мы имеем, что cos∟BOC = cos (α - β).
Используя последнее равенство и учитывая, что
ОВ = ОС = R, из равенства (3) можно записать:
![]()
или
![]() (4)
(4)
В равенствах (2) и (4) равны их левые части, а значит, должны быть равными и их правые части:
![]()
Отсюда имеем:
![]()
Формулу (5) называют формулой косинуса разности двух углов.
Определение: Косинус разности двух углов равен сумме произведения косинусов этих углов и произведения синусов этих углов.
![]()
Определение: Косинус суммы двух углов равен произведению косинусов этих углов минус произведение синусов этих углов.
![]()
Определение: Синус суммы двух углов равен произведению синуса первого угла на косинус второго плюс произведение косинуса первого угла на синус второго.
![]()
Определение: Синус разности двух углов равен произведению синуса первого угла на косинус второго минус произведение косинуса первого угла на синус второго.
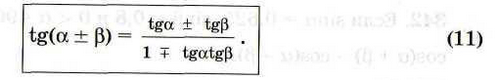
3. Первичное закрепление:
Решить №343, 347
4. Рефлексия.
Постановка Д/з №