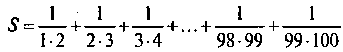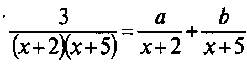Урок на тему 'Представление дроби в виде суммы дробей' (8 класс)

Тема урока:

ПРЕДСТАВЛЕНИЕ ДРОБИ В ВИДЕ СУММЫ ДРОБЕЙ

Цели:

1. изучить метод неопределённых коэффициентов;

2. формировать умение представлять рациональную дробь в виде суммы дробей;

3. развивать умственные способности и логическое мышление учащихся.

Тип урока: объяснение новой темы

Оборудование к уроку: проектор, раздаточный материал

Ход урока

1. Организационный момент (1 слайд)

- Здравствуйте ребята, присаживайтесь. Сегодняшний урок я хотел бы начать со следующих слов.

«Доброе утро»

Пусть каждый день и каждый час

Вам новое добудет.

Пусть добрым будет ум у вас,

А сердце умным будет.

С. Маршак

- И вот с таких хороших слов и мы начинаем наш урок. А начнем с устной работы. Обратите внимание на экран.

2. Устная работа

1 задание: Установите соответствие между графиками функций и формулами, которые их задают.

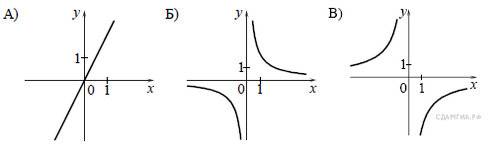
1) ; 2) ; 3) ; 4)

2 задание: Вычислить (3,6 + 1,6 0,25 ) : 0,8 =

3 задание: Представить в виде дроби: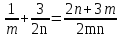

4 задание: Решить систему уравнений: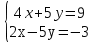

5 задание: Представить выражение в виде дроби: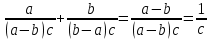

6 задание: Подставьте знаки и выполните действия: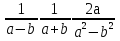

- Молодцы! А теперь продолжая наш урок проведем небольшую самостоятельную работу.

3. Самостоятельная работа (на карточках)

I вариант

1 задание: Установите соответствие между графиками функций и формулами, которые их задают.

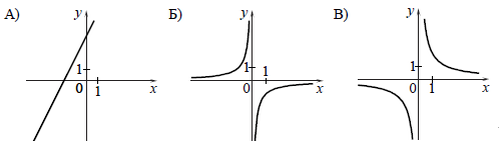
1) ; 2) ; 3) ; 4)

2 задание: Преобразуйте в дробь выражение

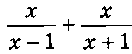
3 задание: Преобразуйте в дробь выражение

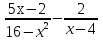
II вариант

1 задание: Установите соответствие между графиками функций и формулами, которые их задают.

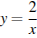
1) ; 2) ; 3) ; 4)

2 задание: Преобразуйте в дробь выражение

3 задание: Преобразуйте в дробь выражение

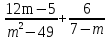
- Молодцы! На следующем уроке я вам сообщу ваши оценки по данной работе.

4. Объяснение нового материала (пример 1 - метод неопределенных коэффициентов)

- Посмотрите, теперь на доску. Мы уже умеем представлять сумму дробей в виде одной дроби. А возможно ли обратная задача? Сможем ли мы представить дробь в виде суммы дробей? (Ответы учащихся).

- А давайте попробуем! И в этом нам поможет, так называем метод неопределенных коэффициентов.

Решение примера 1 из учебника

Умение складывать рациональные дроби оказывается полезным и при нахождении сумм обыкновенных дробей.

Например, для нахождения суммы дробей:

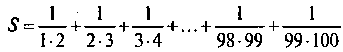
Можно применять формулу:

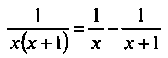
т.е. представить интересующую нас дробь в виде разности двух более простых дробей.

Также эту формулу можно применить для упрощения выражений вида:

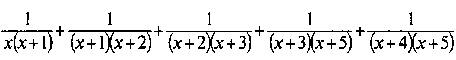
- Давайте немного отдохнем и проведем физминутку.

5. Физминутка

- Спасибо, молодцы! Присаживайтесь и продолжаем наш урок.

6. Объяснение нового материала (пример 2 - деление уголком)

- Ребята давайте вспомним, как мы выделяли целую часть из неправильной дроби? (Ответы учащихся). Сможем ли мы выделить целую часть у рациональной дроби?

- Оказывается да, и данный метод получил название деление уголком.

Решение примера 3 из учебника.

7. Закрепление новой темы. Решение номеров 197, 200 а)

8. Итоги урока.

9. Домашние задание: 198, 201а).

Творческое задание. Найти сумму дробей: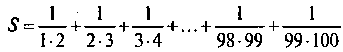

10. Обучающая самостоятельная работа на закрепление с последующей проверкой

I вариант

II вариант