Урок 'Деление многочленов' 10 класс

Тема урока «Деление многочленов»

«Люди, незнакомые с алгеброй,

не могут представить себе

тех удивительных вещей,

которых можно достигнуть

при помощи названной науки»

Г. Лейбниц

Цели урока:

1.Обучающая - показать использование теории многочленов в решении алгебраических задач;

2.Развивающая - развивать умения самостоятельного решения типовых задач, связанных с преобразованием многочленов;

3.Воспитывающая - воспитывать чувство ответственности, желание расширить и углубить знания, полученные на уроке.

План урока:

1) Организационный момент

2) Устная работа

3) Решение типовых задач

4) Задача с параметрами

5) Задача из ЕГЭ

6) Уравнение

7) Домашнее задание

8) Итог урока

1. Организационный момент (постановка темы, цели урока)

Задачи, в которых встречается деление многочленов, играют огромную роль в формировании логического мышления и математической культуры. Решение таких задач весьма полезно еще и потому, что они раньше встречались на вступительных экзаменах во многих престижных вузах, а сейчас это - задания из части С ЕГЭ.

2. Устная работа

Найдите ошибку!

Совет учиться на ошибках другого бесполезен,

научиться чему-либо можно только на собственных ошибках.

Бернард Шоу

1.Многочленом нулевой степени называется многочлен, все коэффициенты которого равны нулю.

2.Коэффициент при старшем члене многочлена называют степенью многочлена.

3.Число α называется корнем многочлена Р(х), если Р(α)≠0.

4.Многочлен f(х) делится на многочлен s(х) не являющийся нулевым многочленом, если:

a) f(х) = s(х)•q(х) + r(х);

б) deg s(х) < deg r(х) или r(х)=0

5.Остаток от деления многочлена Р(х) на двучлен (х + α) равен Р(α), т.е. значению Р(х) при х = α.

6.Схема Горнера позволяет находить неполное частное и остаток от деления многочлена f(х) на двучлен s(х) = х + α.

7.Рациональные корни неприведённого уравнения с целыми коэффициентами являются делителями его свободного члена.

8. Многочлены называются тождественно равными, если равны соответствующие показатели степеней одночленов.

Устная работа

1. Найдите степень суммы многочленов: х³ + 3х² + 1 и х⁵ + х⁴ + 6х² - 1.

2. Найдите степень произведения многочленов: (х² - 1)(х³ + 1)(х + 1) и (х - 1)³(х + 1)²

3. Найдите остаток от деления многочлена f(x) = х⁵ - 4х⁴ + 5х³ - 2х² + 7х - 1 на (х - 1)

4. Является ли число 2 корнем многочлена f (x) = х⁴ - 2х³ + 8 х² - х - 1?

5. Делится ли многочлен f (x) = х⁵ - 7х³ + х² + 13х + 6 на (х + 1) нацело?

6. Найдите свободный член многочлена (х² - х + 1)2012 + (х² - х + 1)2012

7. Найдите сумму коэффициентов многочлена (х - 1)2012 + (х + 1)2012.

3. Решение типовых задач

Какие вы знаете приемы деления многочленов?

• деление углом

• метод неопределенных коэффициентов

• Схема Горнера

1) Разделите «уголком» многочлен 4х⁴-2х³-16х²+5х+9 на многочлен х²-2х-1

Ответ ;

2) Применяя схему Горнера, найти частное и остаток от деления многочлена

6х⁴-5х³-53х²+45х-9 на многочлен х-2

Ответ: Q = , R = - 75;

3) Методом неопределенных коэффициентов найти частное и остаток от деления P(x) на Q(x).

P(x) = 5х⁴-х³-х-4

Q(x) = х²-4

4. Задача с параметрами

Найти все значения параметров а и b, при которых многочлен Р(х) делится нацело на многочлен Q(х):

Р(х)=6х⁴-х³+ах²+bх+4, Q(х)=х²-4;

5. Задача из ЕГЭ

Лысенко . Подготовка к ЕГЭ 2011. Вариант 14.(стр. 109)

Найдите все целые значения m, при которых число является целым.

Ответ :-8, -4, -2, 2.

Выполнить самостоятельно

При каких натуральных значениях выражение 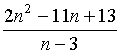является целым числом?

РЕШЕНИЕ. Разделим числитель дроби на знаменатель с остатком:

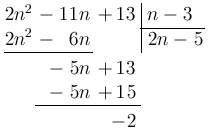
Таким образом, исходное выражение равно , что является целым числом тогда и только тогда, когда нацело делится на . Поскольку целыми делителями числа являются числа и только они, получаем
ОТВЕТ: .

6. Решить уравнение:

Р е ш е н и е . x ³ - 3x ² - 13x + 15 = 0 .

Ищем первый корень перебором чисел: 0, 1, 2, 3

и подстановкой в уравнение. В результате находим,

что 1 является корнем. Тогда делим левую часть этого

уравнения на двучлен x - 1, и получаем:

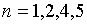
Теперь, решая квадратное уравнение: x ² - 2x - 15 = 0,

находим оставшиеся два корня: x₁ = - 3 и x₂ = 5 .

Ответ: -3; 1; 5.

7. Домашнее задание:

8. Итоги урока

Дополнительное задание:

Назовите корни уравнения