Бинарный урок: Эта Удивительная производная

Тема урока: «Эта удивительная производная»

Цели:

• Показать на примерах применение дифференциального исчисления для решения задач с практическим содержанием.

• Закрепить умения, навыки исследования функций с помощью производной.

• Формировать умения переводить описания реальных ситуаций на формальный математический язык, т. е. переходить от реальных ситуаций к их математическим моделям.

• Воспитывать аккуратность, внимательность, умение работать в паре.

• Активизировать познавательную деятельность учащихся путем решения задач с практическим содержанием.

«Мыслить последовательно,

судить доказательно,

опровергать неправильные выводы

должен уметь всякий: физик и поэт,

тракторист и химик».

Эрнест Кольман.

Ход урока:

1.Организационный момент. Здравствуйте! Тема нашего урока «Эта удивительная производная». И сегодня мы попытаемся, насколько это возможно, в рамках одного урока рассмотреть эту тему.

Активизация знаний учащихся На одном из первых уроков изучения производной я вам задала вопрос:

Мы изучаем производную. А так ли это важно в жизни?

Вы на него не смогли ответить, т.к. у вас не хватило соответствующих знаний. И тогда я вам предложила поработать над проектами, т.е. провести самостоятельное исследование по теме «Производная и её применение в различных областях науки».

Вам было предложено 4 темы, список литературы, которым я вас не ограничивала. Но одним из условий выполнения этой проектной работы было то, что пользоваться можно было только книгами, журналами, справочной литературой, помощью консультантов и т. д.. И акцентировала ваше внимание на том, что нельзя было пользоваться интернетом. И сегодня мы увидим насколько успешно вы справились с задачей самостоятельного отбора и перерабатывания информации.

Итак ,рассмотрим работы творческих групп, которые провели самостоятельные исследования по темам. Еще раз убедимся в важности роли производной в исследовании процессов окружающего мира, покажем практическую необходимость и теоретическую значимость нашей темы.

С первым проектом выступят………….

2.Как родилась производная?(Историческая справка-презентация)

• Ферма далеко продвинулся в применении дифференциальных методов, он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей. Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему.

• В 1638 году Ферма поделился этим открытием со своим земляком Рене Декартом, который также занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым.

• Тем не менее, выдвинутые идеи не пропали впустую. Многие из них легли в основу нового метода математического анализа - дифференциального исчисления, основоположниками которого считаются Вильям Лейбниц и Исаак Ньютон.

Вильгельм Лейбниц (1646-1716) Исаак Ньютон (1642-1727)

Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления

Жозеф Луи Лагранж Леонард Эйлер Карл Фридрих Гаусс

(1736-1813) (1707-1783) (1777-1855)

3.Устная работа.

Внимание!

Пришло время поработать!

1. В чем заключается геометрический смысл производной?

2. Что называется производной функции в точке?

3. В чём состоит механический смысл производной ?

4. (x³ )' ?

5. (1 ⁄ √x)' ?

6. tg' x ?

7. (Сtg3x)' ?

8. (2х+ Sin x)' ?

9. (2х+6)' ?

Мы рассмотрели вопросы теории, но математические методы не могут применяться непосредственно к действительности, а применимы только к математическим моделям того или иного явления. Математическая модель отображает основные свойства и характеристики реального явления.

В математические модели экстремальных задач входит функция, которую надо составить по условию и найти ее оптимальное значение на промежутке изменения аргумента.

Однако в одной и той же задаче в разных ситуациях наилучшими могут быть совершенно разные решения. Все зависит от выбранного критерия.

Вашему вниманию предлагается различные поперечные сечения канала в форме трапеции. Они могут быть использованы в разных целях

Таблица.

10. Рис. 2

Рис. 1 Рис. 3

Предлагается учащимся выбрать различные критерии:

1) канал должен был судоходным (глубина);

2) канал должен вмещать наибольшее количество воды (объем);

3) канал служит водоемом на птицефабрике (площадь поверхности);

4) необходимо, чтобы на облицовку его боковых стенок и дна пошло наименьшее количество материала (площадь).

Как видим, модель одна, а практических задач несколько.

Практические приложения производной.

Математическое моделирование применимо в различных

областях знаний, поэтому и производную можно использовать не только в математике, но и в смежных с ней дисциплинах.

Основные этапы моделирования, при решении задач прикладного характера:

1. Изучение реальной ситуации или явления;

2. Формализация - построение математической модели на языке уравнений;

3. Разработка алгоритма решения этих уравнений;

4. Получение результатов и их анализ и интерпретация.

5. Компьютерный эксперимент.

4.Решение прикладных задач.

Метод, основанный на теореме о произведении нескольких множителей.

Теорема1. Произведение нескольких положительных множителей, сумма которых постоянна, имеет наибольшее значение при равенстве множителей.

max при

Задача 1.Над центром круглого стола на блоке висит лампа. На какой высоте следует поместить эту лампу, чтобы на краях стола получить наибольшую освещенность?

Решение:

Сила света , где k - коэф-нт пропорц.

, где X- радиус стола. Имеем:

Величина достигает максимума при тех же значениях, что и I.

Откуда

поэтому по теореме

наибольшее значение Z достигает, если:

то есть при , откуда . Значит

Показать решение наглядно, т. е. собрать цепь для освещения стола.

2.Метод, основанный на теореме о произведении 2-х множителей

Теорема2. Произведение двух множителей, сумма которых постоянна, имеет наибольшее значение при равенстве множителей.

max при

Задача 2. Русла двух рек (в пределах некоторой области) представляют собой

параболу у=х² и прямую х-у-2=0. Требуется соединить эти реки прямолинейным каналом наименьшей длины. Через какие точки следует его провести?

Решение через свойства касательных.

Задача 3. Печатный текст (вместе с промежутками между строками) одной страницы книги должен занимать 400 см². Верхние и нижние поля страницы должны иметь ширину 2 см. Боковые - 4 см.

Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?

Решение через производную.

</<font size="3">

Задача 4. Окно имеет форму прямоугольника, завершенного полукругом. При заданном периметре найти размеры окна, чтобы оно пропускало наибольшее количество света.

Решение.

1 способ. Метод, основанный на теореме о квадратных трехчленах.

Теорема3. Квадратный трехчлен имеет

экстремальное значение, принимаемое им при

Причем, если a < 0, то оно наибольшее, если а > 0 оно наименьшее.

Решение. Модель задачи находим так же как в первом случае.

, а решать буде м по теореме 3.

Известно, что квадратный трехчлен принимает наибольшее значение при

2 способ (через производную.)

3 способ ( проверяем через компьютер).

Теперь, когда математическая модель составлена, давайте перейдем к этапу компьютерного моделирования. Создадим на ЯП Паскаль программу, вычисляющую максимальное значение функции на интервале от а до в, просматривая изменение аргумента х с шагом 1. Функцию зададим с помощью вспомогательного алгоритма FUNCTIОN.

Var a,b,t,M,R :integer;

Const

P=6;

Pi=3.14;

Function F(x:integer):integer;

begin

F:=

end;

BEGIN

a:=0; b:=6;

M:=a; R:=F(a);

for t:=a to b do begin

if (F(t)>R)then begin

M:=t;

R:=F(t);

end;

end;

write(M);

END.

Данное решение поможет эффективно подготовиться к решению задачи повышенного уровня сложности В14 в ЕГЭ по информатике.

Для моделирования решения следующих задач воспользуемся средствами в Ms. Excel.

Задача 5.

Отпуск товара со склада производится по закону: ,

где х - время отпуска товара в часах. Через сколько часов скорость отпуска товара будет наименьшей?

Решение. Построим график производной данной функции и найдем, при каком значении аргумента значение производной равно 0.

Столбец А заполним значениями аргумента х, а столбец В - значениями производной функции. С помощью мастера диаграмм построим график производной функции:

По графику определим значение аргумента, при котором значение производной равно 0. Это точка - 75.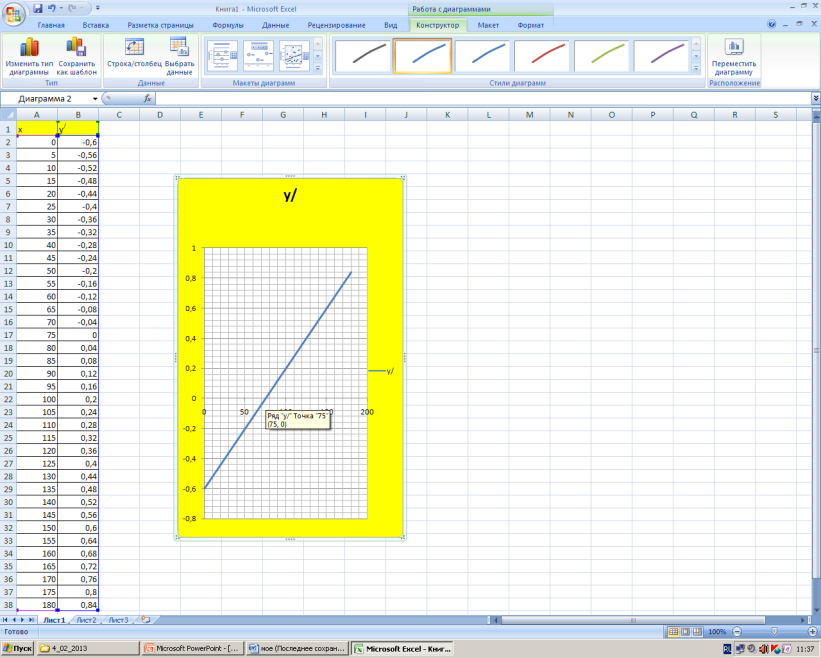

Задача 6.

Количество зеленой массы растений в регионе изменяется по закону:

,

где х - время в годах. Через сколько лет прирост зеленой массы растений будет наименьшим.

Решение. Построим график производной данной функции и найдем, при каком значении аргумента значение производной равно 0.

Столбец А заполним значениями аргумента х, а столбец В - значениями производной функции. С помощью мастера диаграмм построим график производной функции:

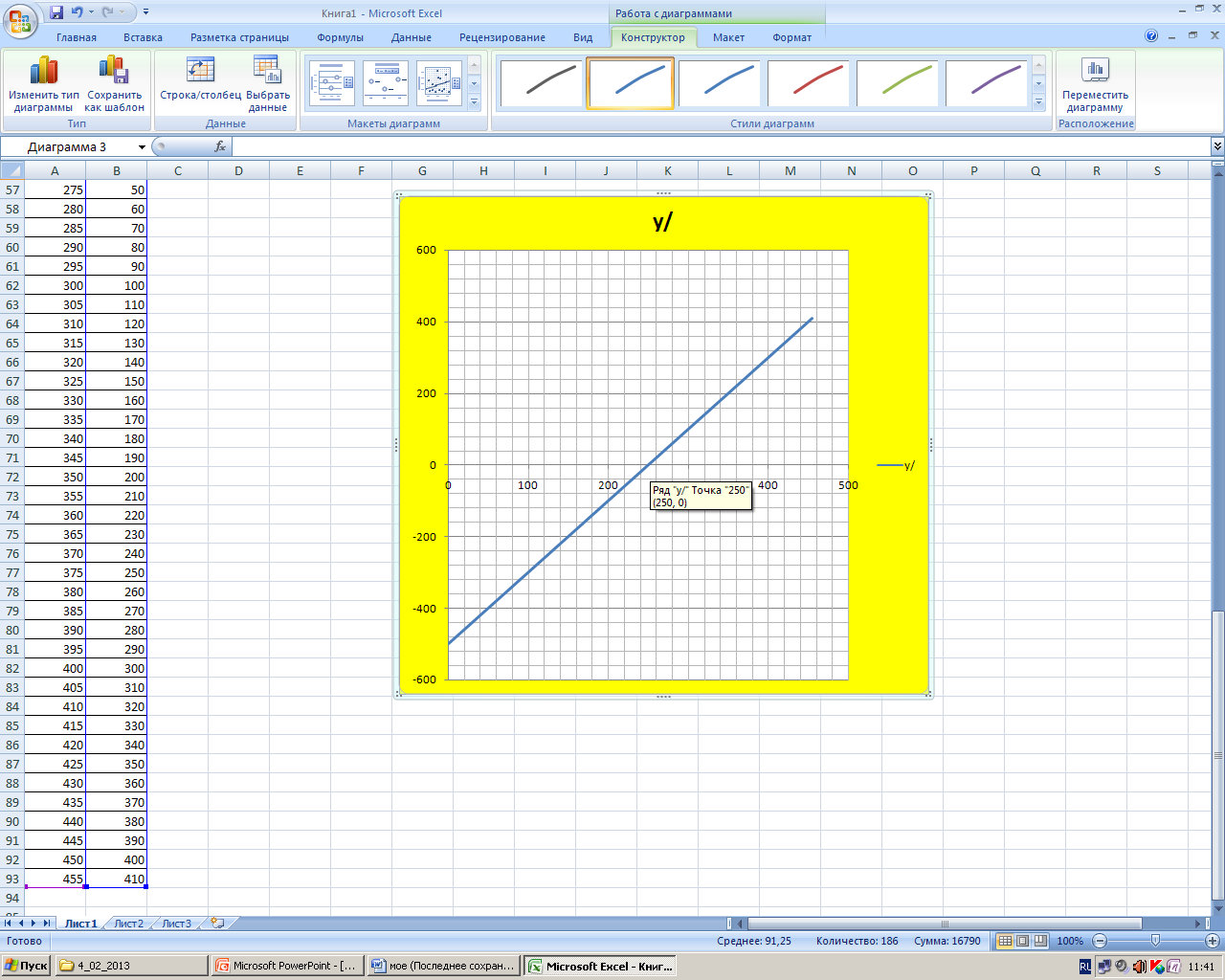
Задача 7.

Объем произведенного товар выражается формулой: ,

где х - время в сутках. Найдите скорость освоения объема работ.

Решение. Построим график производной данной функции и найдем, при каком значении аргумента значение производной равно 0.

=0,

Столбец А заполним значениями аргумента х, в столбце В - произведем перевод градусов из столбца А в радианы, так как Excel работает с радианами (воспользуемся формулой: ), а столбец С заполним значениями производной функции.

С помощью мастера диаграмм построим график производной функции:

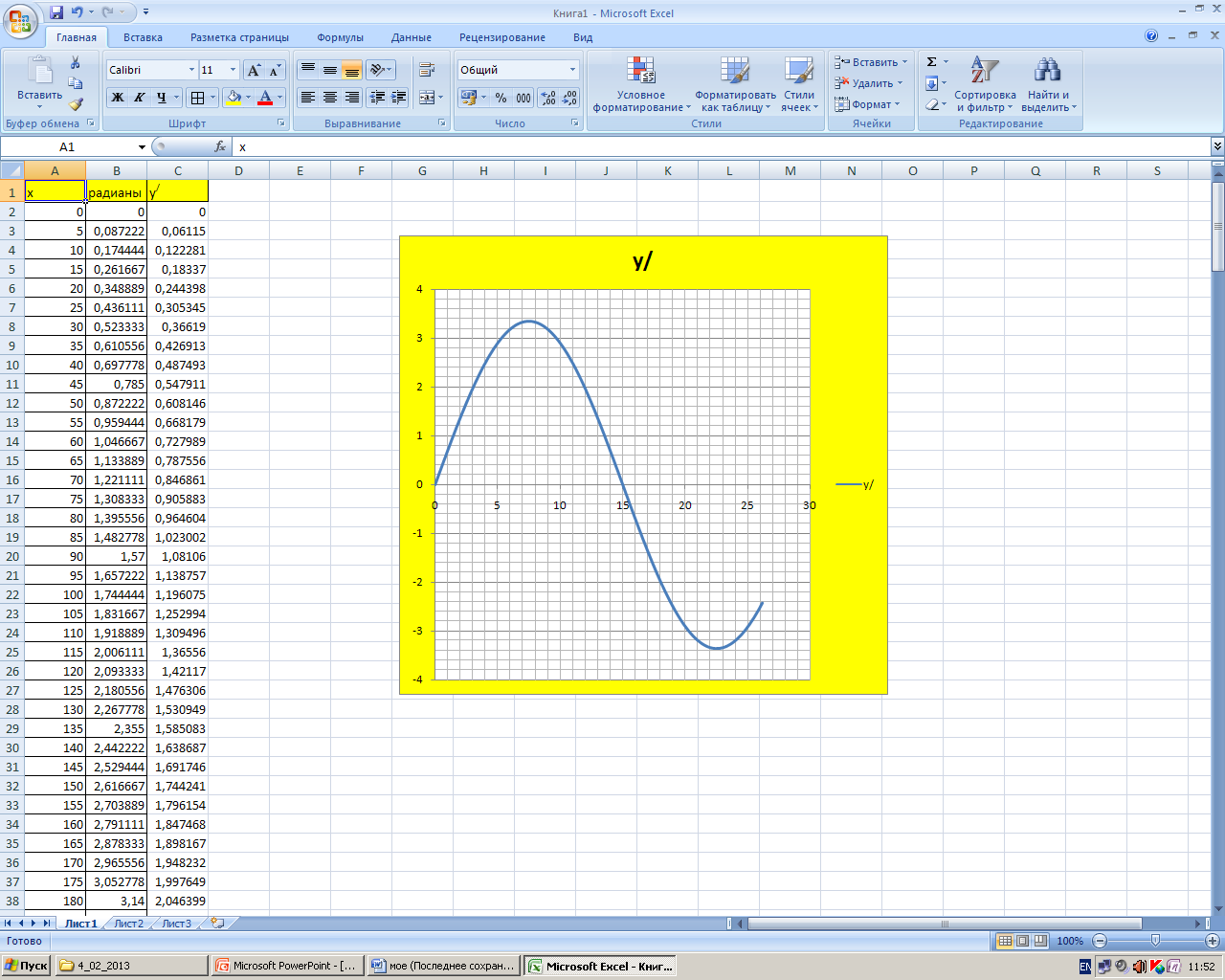
Вывод. Сегодня на уроке мы решали задачи, связанные с различной деятельностью человека. Но их объединяет - способ решения. Мы переходили от реальных ситуаций к их математическим моделям. Мы убедились, что такое абстрактное понятие, как производная, помогает решать много жизненных задач.

Урок хочется закончить словами американского математика Мориса Клайна:

"Музыка может возвышать или умиротворять душу,

Живопись - радовать глаз,

Поэзия - пробуждать чувства,

Философия - удовлетворять потребности разума,

Инженерное дело - совершенствовать материальную сторону жизни людей,

А математика способна достичь всех этих целей"

Домашняя работа

По информатике: демо-версия ЕГЭ информатика 2012 В14.

По математике:

1. Известно, что тело массой 5 кг движется прямолинейно по закону

s(t)= t²+2. Найдите кинетическую энергию тела через 2 с после начала движения.

2. Найдите силу F, действующую на материальную точку с массой 10 кг, движущуюся прямолинейно по закону х(t) = 2t³- t² при t = 2с.

3. Закон изменения температуры тела в зависимости от времени задаётся уравнением T = 0,2t². С какой скоростью изменяется температура тела в момент времени 5с ?

4. Изменение силы тока в зависимости от времени задано уравнением

I = 2t² - 5t. Найдите скорость изменения силы тока в момент времени 10 с.

5. Маховик вращается вокруг оси по закону (t) = t⁴ - 1. Найдите его угловую скорость w в момент времени t и t=2 с.

6.(2) При вращении проволочной рамки в однородном магнитном поле пронизывающий рамку магнитный поток изменяется в зависимости от времени по закону Ф = 10^-2cos 10 t. Вычислив производную Ф^,_t , написать формулу зависимости ЭДС от времени = (t).

7. (2) Заряд q на пластинах конденсатора изменяется по закону

q = 10 ^{- 6}cos 10 ⁴t. Записать закон зависимости силы тока от времени i= i(t), вычислив производную q^,_t.