Урок №

Тема: «Решение систем линейных уравнений способом подстановки».

Цель урока:

- обучающие: ввести алгоритм решения системы двух линейных уравнений с двумя переменными способом подстановки, сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки;

- развивающие: развивать умения анализировать, делать выводы, развивать внимание;

- воспитательные: развивать познавательный интерес через моменты взаимоконтроля, взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.

Тип урока: изучение нового материала.

Этапы урока:

№

Этап урока

Время

Задачи этапа

1.

Организационный момент

1 мин.

2.

Проверка домашнего задания

3 мин.

Проверка правильности выполнения домашнего задания.

3.

Актуализация опорных знаний учащихся

5 мин.

Повторить основные определения; активизировать осознанность применения знаний при решении задач.

4.

Изучение нового материала

15 мин.

Знакомство учащихся с алгоритмом решения системы двух уравнений с двумя переменными методом подстановки (обратить внимание на оформление решений)

6.

Закрепления изученного материала

15 мин.

Сформировать умение решать системы уравнений методом подстановки

7.

Подведение итогов

4 мин.

Повторить изученное на уроке

8.

Домашнее задание

2 мин.

Инструктаж по домашнему заданию

Ход урока.

Этап №1

Слайд №1.

Приготовились к уроку, встали у своих мест.

-Здравствуйте, ребята. Сегодня у нас на уроке присутствуют гости, поздоровайтесь, пожалуйста, садитесь.

Слайд №2

Мы с вами начинаем очередной рабочий урок и эпиграфом к нему я подобрала следующее высказывание И. Гёте: «Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю». Так вот мы с вами сегодня будем пытаться стать настоящими учениками, чтобы хоть чуть-чуть почувствовать себя учителем.

Цель нашего урока - это вывести алгоритм решения системы двух линейных уравнений с двумя переменными способом подстановки, сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки.

Этап№2

На прошлом уроке мы с вами познакомились с новой математической моделью.

Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Перед нами стояла задача найти такие пары значений (х; у), которые одновременно удовлетворяют и первому, и второму уравнению.

-Кто может мне сказать:

Что называется решением системы двух линейных уравнений с двумя переменными?

Слайд№3. (открыть после ответа уч-ся).

-Хорошо.

-А что значит решить систему двух линейных уравнений с двумя переменными?

Слайд №4. (открыть после ответа уч-ся).

-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).

Проверим домашнее задание.

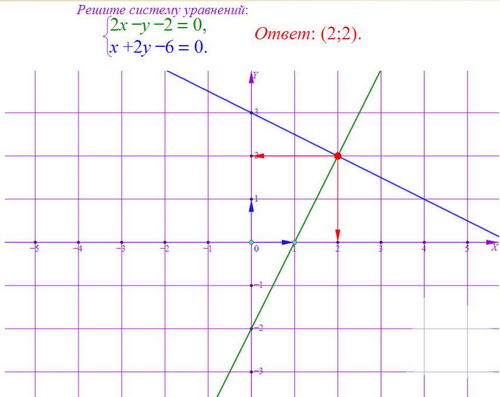
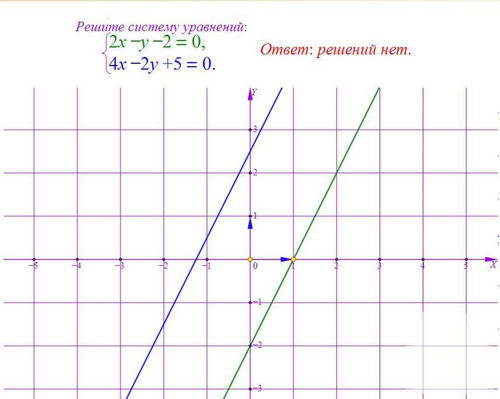
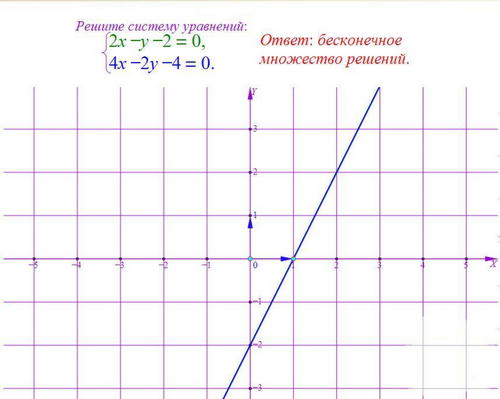
-Пока мы будем проверять домашнее задание, у доски нам решит систему графическим методом…(вызвать ученика к доске, задание на карточке).

Открыли тетради, взяли зеленую пасту, проверяем:

Слайды №5, №6, №7, №8, №9, №10.

-У кого не было ошибок, может поставить себе «5», у кого были помарки, исправления, неточности - зеленой пастой пишут: Домашнее задание проверено.

-Дома, я также просила поработать вас с текстом параграфа №27, и найти ответ на вопрос: «Какие важные выводы можно сделать с помощью графического способа решения систем уравнений?». Кто нашел ответ на этот вопрос? (стр.63 учебника).

Слайд №11. (строки «выпускать» по мере ответа уч-ся).

-ученик закончил решение системы. Сейчас он прокомментирует нам ее решение.

-Спасибо, садись.

Этап№3

-А сейчас, внимание на экран, я хочу показать вам решение графическим методом еще одной системы:

Слайд№12.

- На чертеже: построен синим цветом график первого линейного уравнения и зеленым цветом график второго уравнения. Как видите, графики пересекаются.

Координаты точки пересечения графиков и будут являться решением данной системы. Координаты данной точки являются решением и первого и второго линейных уравнений, т.к. точка принадлежит и первому и второму графикам функций. Однако, чему конкретно равны абсцисса и ордината точки, определить очень сложно. Точка «висит» внутри определенной клеточки.

Из этого примера видно, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с дробными значениями координат точки.

Этим мы и займемся сегодня на уроке.

Этап№4

-В тетрадях запишите, пожалуйста, число 17 апреля. Классная работа.

Тема урока: «Решение систем уравнений способом подстановки».

Слайд№13-14.

Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. И так:

№1.

Устный счет

Выразить у через х и х через у:

1. х + 3у = 10 3x-y = 3

2. х + у = 2 5x + 2y = 4

3. 2х + 7у = 8 4x + 2y = 6

4. 6х - 5у = 4 6x - 3y = 9

№2. Попробуем решить систему, которая была вам задана домой, другим способом: (учитель начинает рассуждение, затем продолжают ученики). Слайд №15

Выразим из 2 уравнения x через y:

Подставим в первое уравнение вместо x выражение, которое мы получили

Решаем первое уравнение с одной переменной

Ответ(2;2)

-Чем эти рассуждения отличались от тех, которые вы применяли дома при решении этой системы графическим методом?

-Откройте, пожалуйста, учебник на странице 236 и, прочитав текст, ответьте мне на этот вопрос.

-Как же мы рассуждали? Еще раз по учебнику прочитает нам………..

-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений - почему?

Итак: - выразили

- подставили

- решили

-нашли

-записали ответ

В учебнике найдите алгоритм решения и внимательно прочитайте его.

Слайд№17. («выпускать» строки по мере озвучения уч-ся)

-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди - в старших классах.

Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.

Слайд №18.

-Давайте вернемся к системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске….)

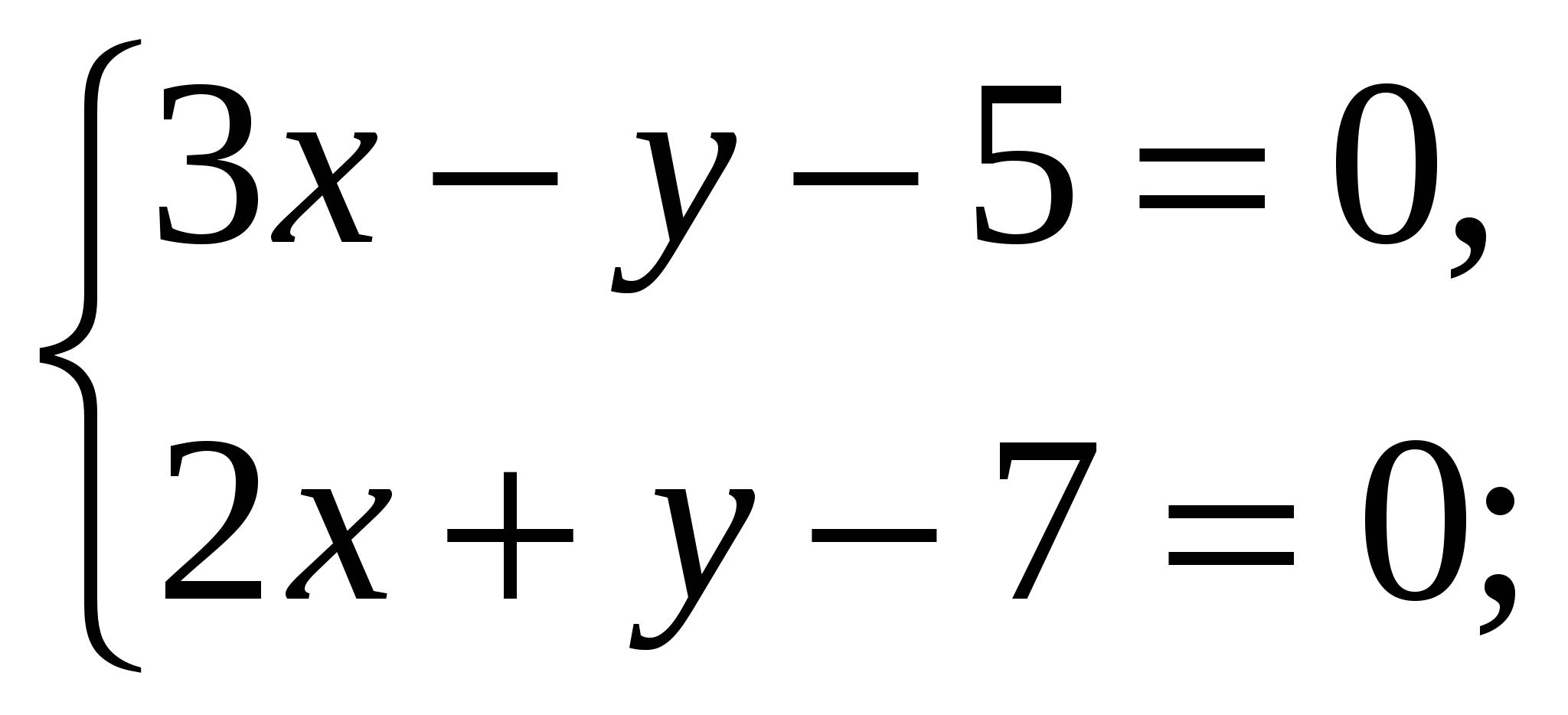
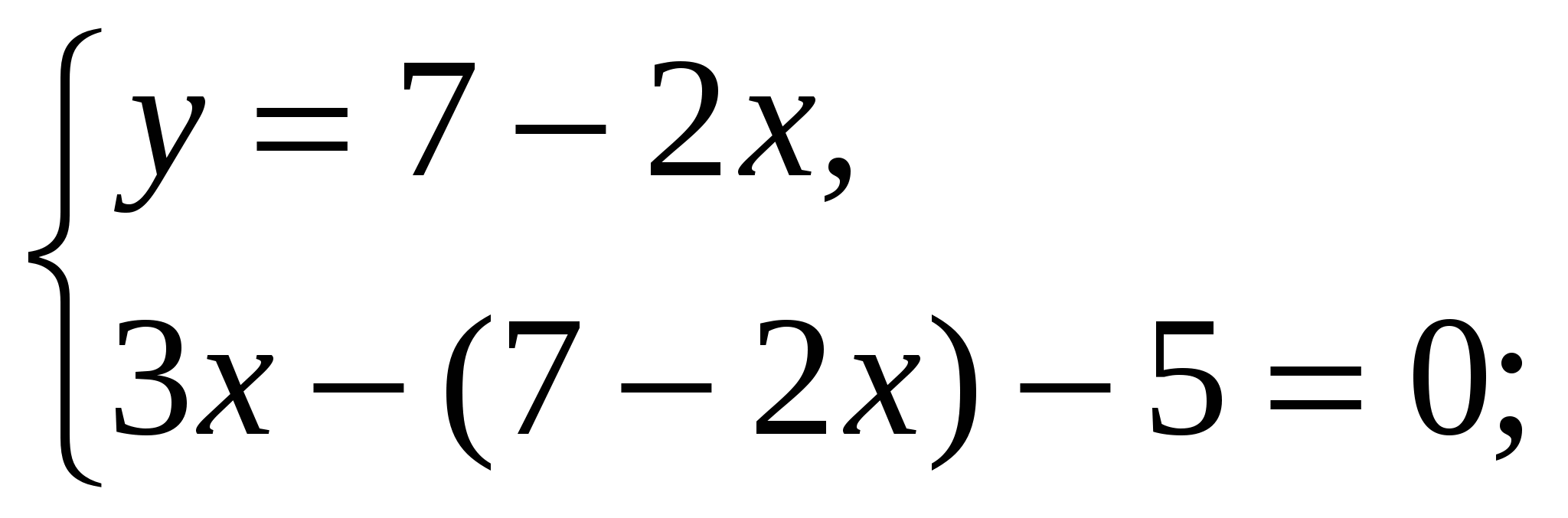
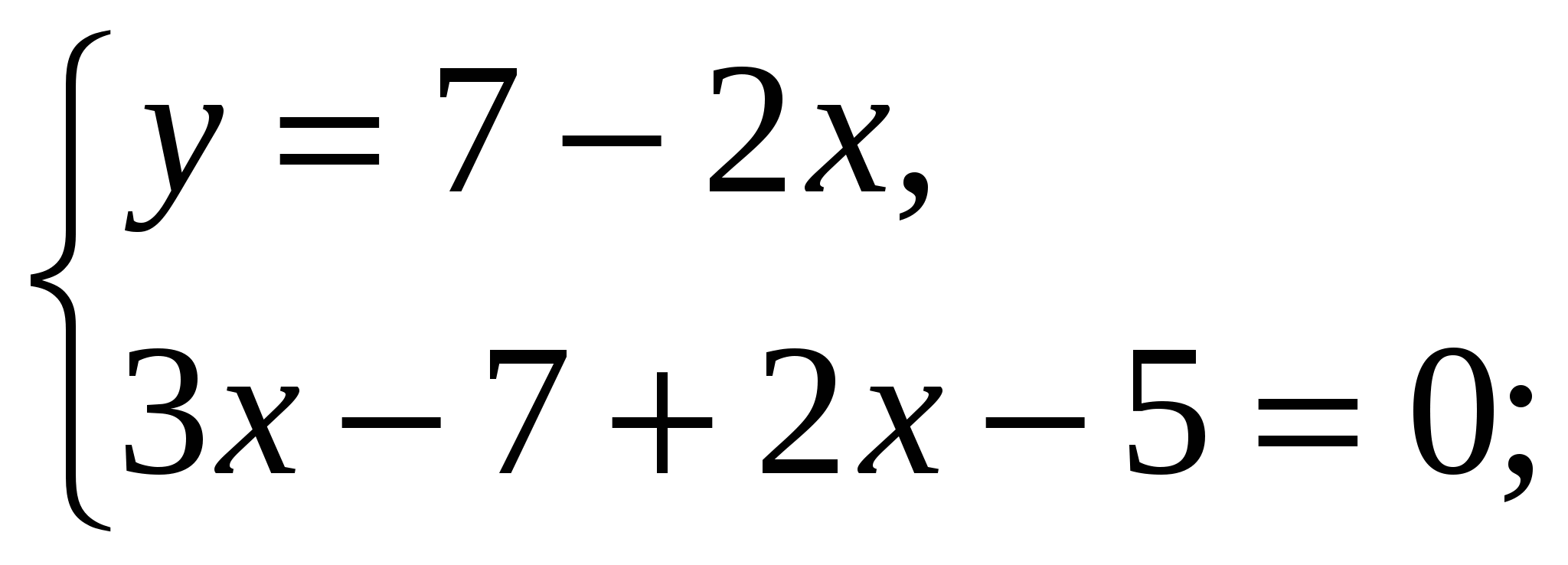
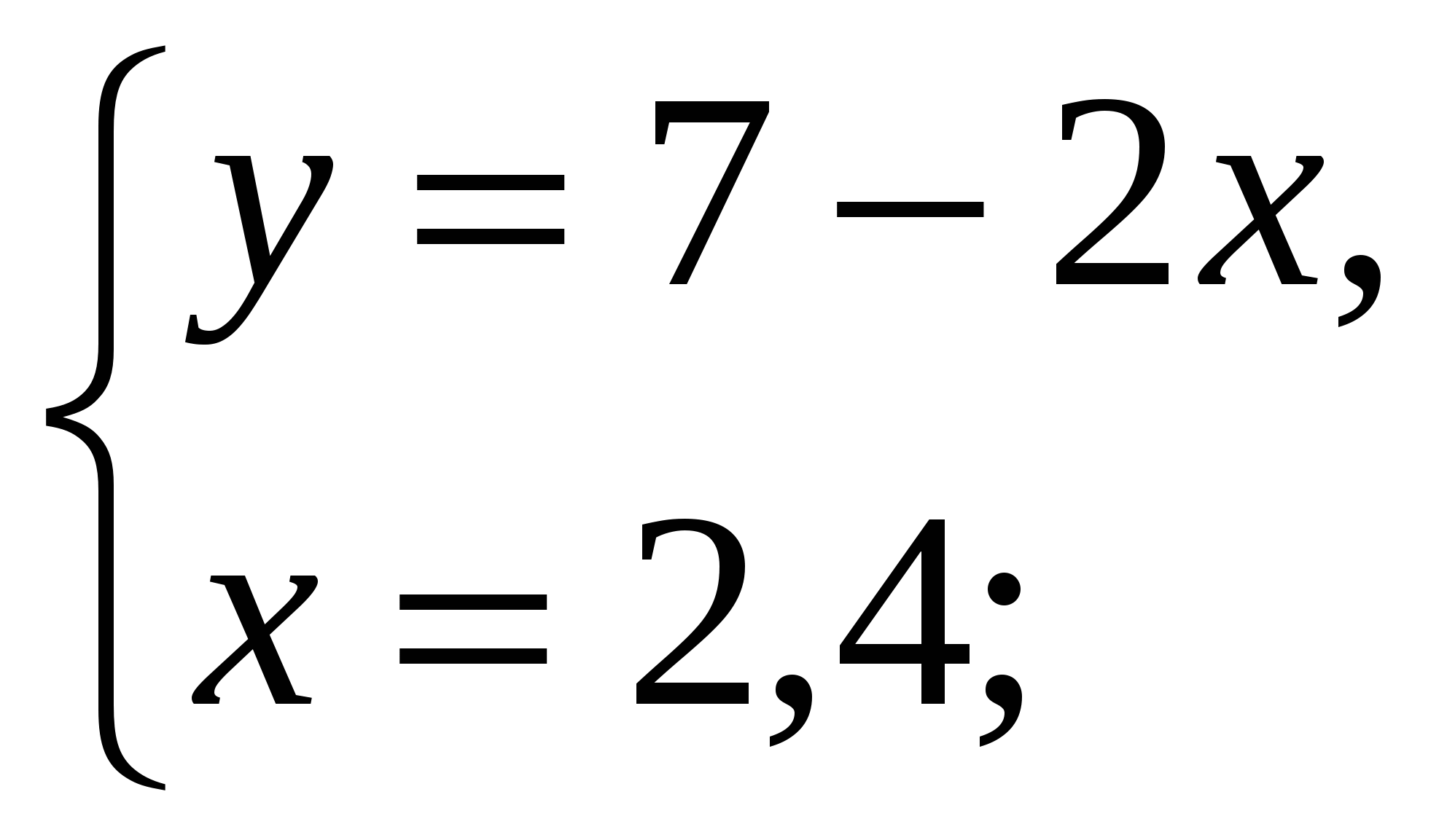
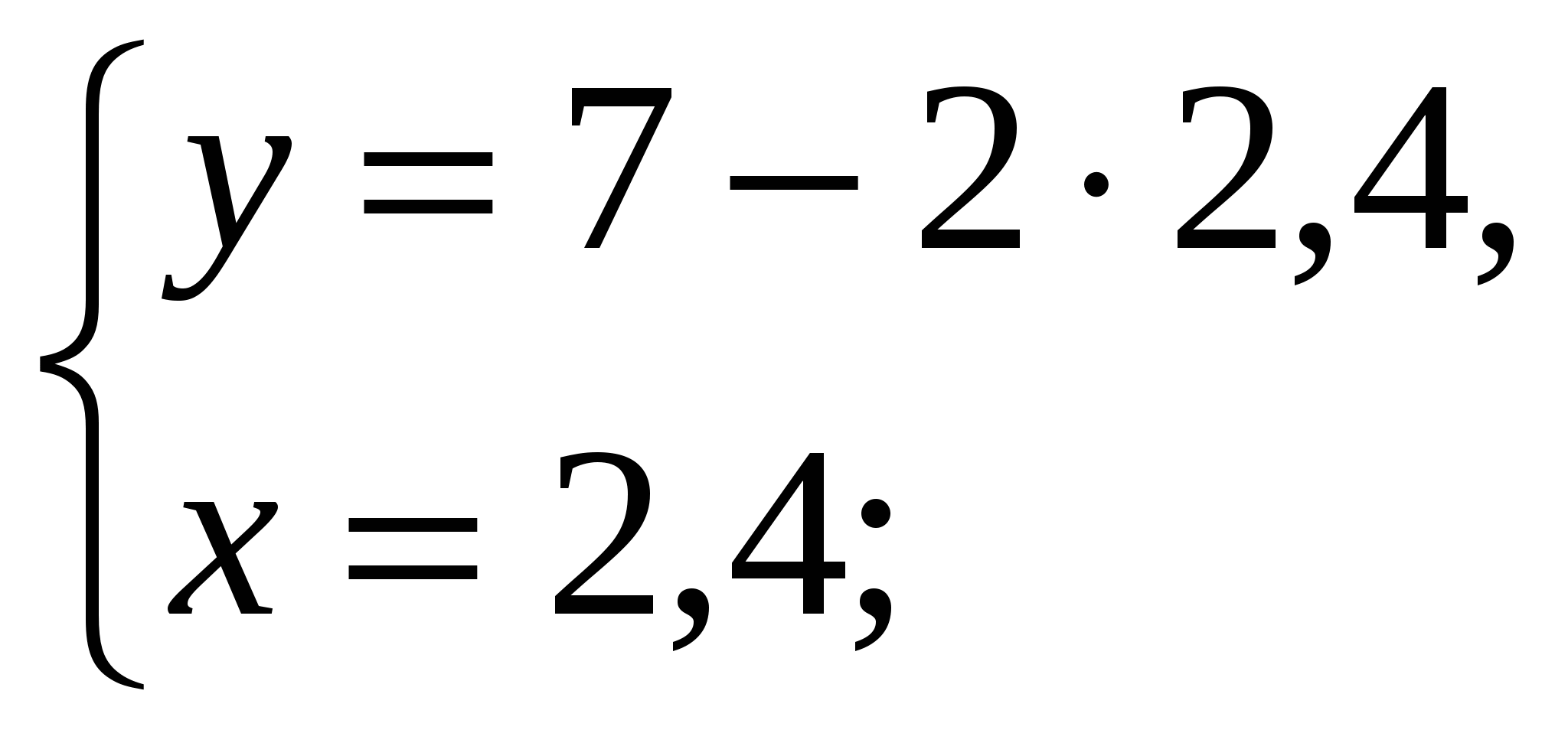
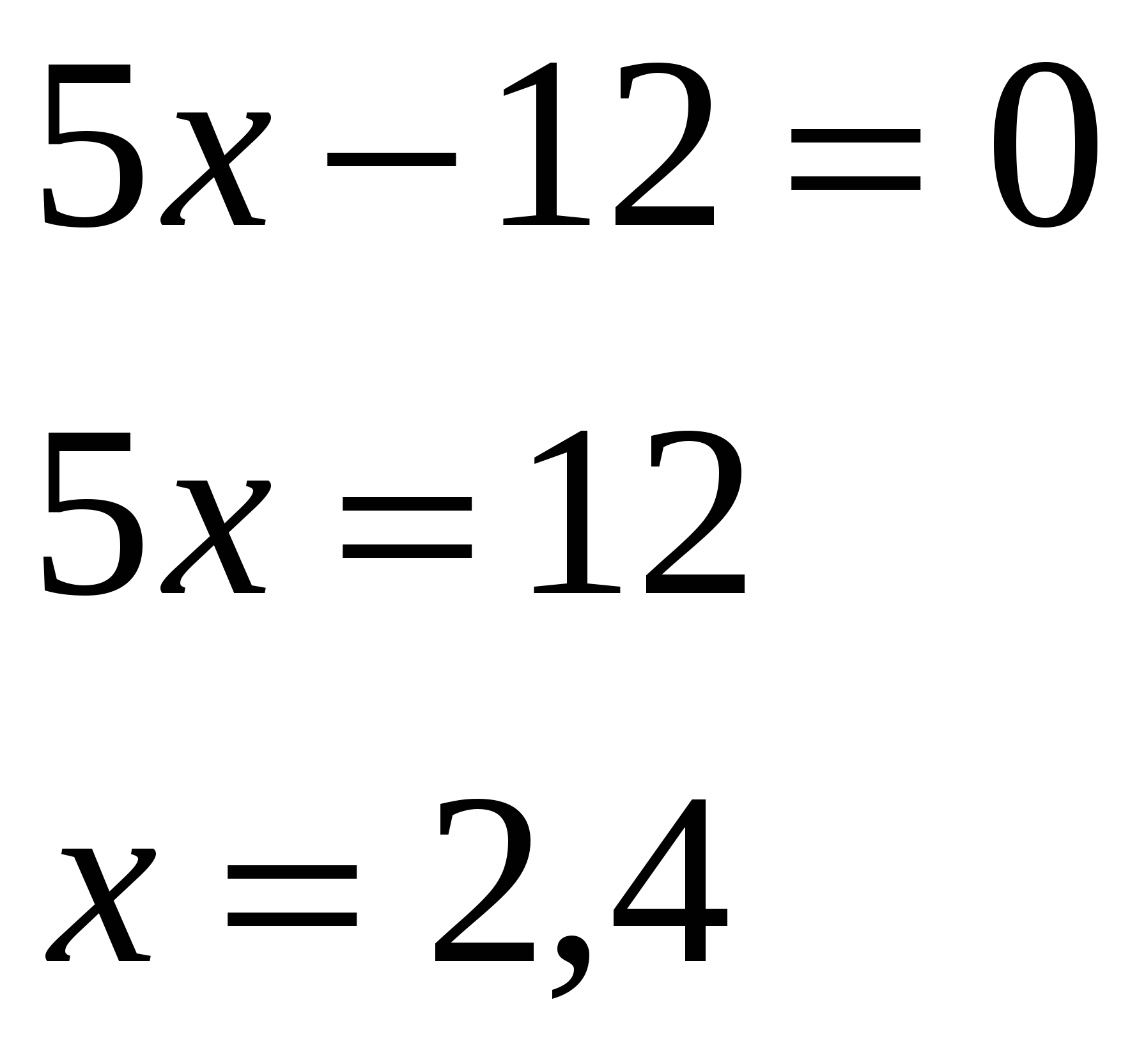
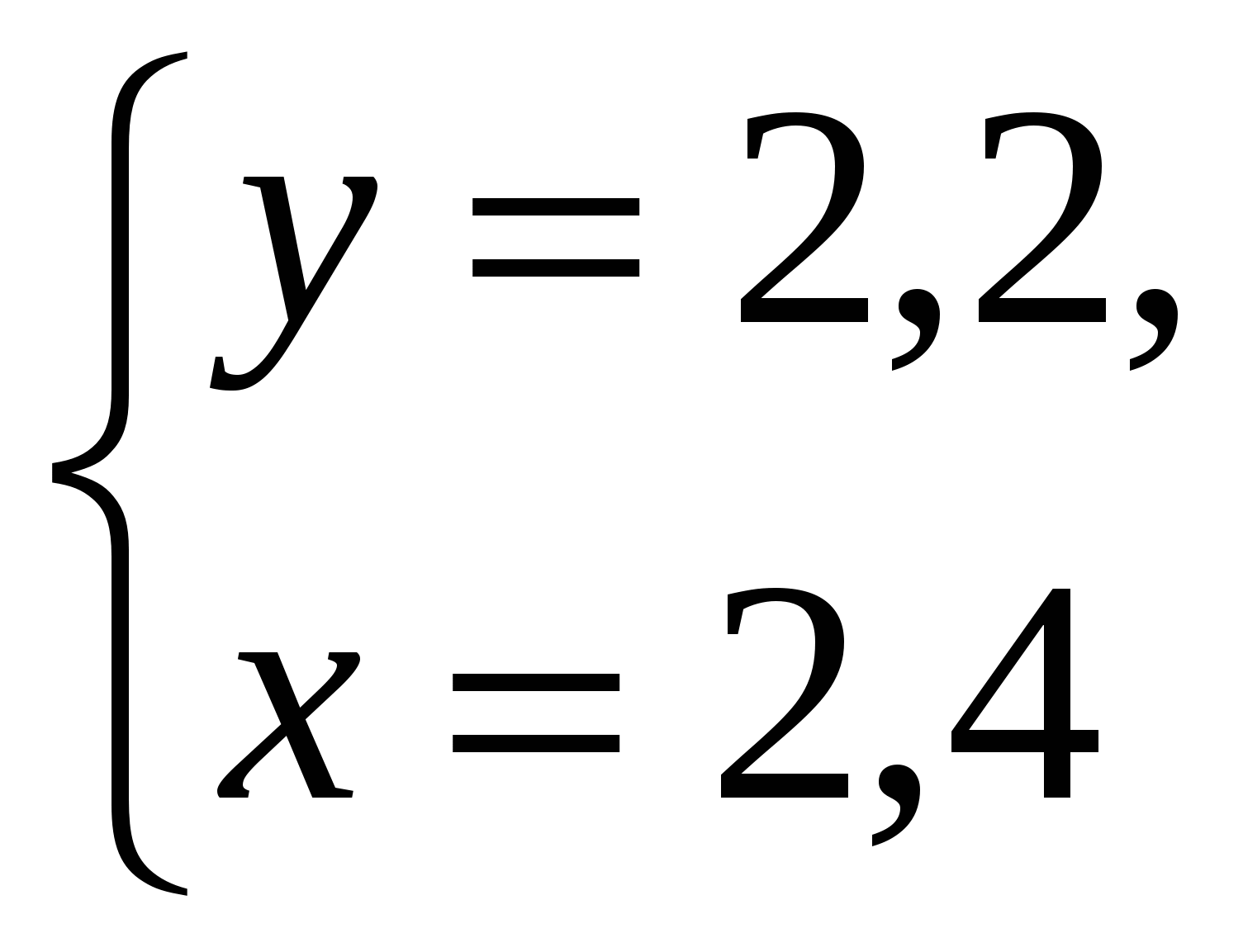Ответ: ( 2,4 ;2,2)

Слайд №19.

Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа)

Теперь будем работать по учебнику стр. 238, № 1086 (а), 1088 (б), 1091 (б).

-Сегодня мы познакомились с вами с еще одним способом решения систем двух линейных уравнений с двумя переменными. Сформулировали алгоритм этого метода. На следующих уроках мы отработаем этот алгоритм на более сложных системах и познакомимся с еще одним очень интересным способом решения.

Домашнее задание: параграф 27 знать алгоритм № 1087, 1090, 1092*.

Оценки сегодня получили:……….

Спасибо за урок. До свидания.