Систематизация теоретического материала за курс геометрии 9 класса

Систематизация теоретического материала

за курс геометрии 9 класса

Лист опроса №3

1. Вектор. Определение.

2. Нулевой вектор. Длина нулевого вектора.

3. Длина или модуль ненулевого вектора.

4. Коллинеарные векторы.

5. Виды коллинеарных векторов.

6. Равные вектора. Определение.

7. Сколько векторов, равных данному, можно отложить от любой точки?

8. Правило треугольника сложения двух неколлинеарных векторов.

9. Правило параллелограмма сложения двух неколлинеарных векторов.

10. Разность векторов.

11. Средняя линия трапеции. Определение.

12. Теорема о средней линии трапеции.

13. Теорема о разложении вектора по двум неколлинеарным векторам.

14. Координаты равных векторов.

15. Правило нахождения координат суммы векторов.

16. Правило нахождения координат разности векторов.

17. Правило нахождения координат произведения вектора на число.

18. Правило и формулы для вычисления координат вектора по координатам его начала и конца.

19. Правило и формулы для вычисления координат середины отрезка.

20. Правило и формула для вычисления длины вектора по его координатам.

21. Правило и формула для вычисления расстояния между двумя точками.

22. Уравнение окружности.

23. Уравнение прямой.

24. Синус угла  из промежутка 0   180.

25. Косинус угла  из промежутка 0   180.

26. Тангенс угла .

27. Основное тригонометрическое тождество.

28. Формулы приведения.

29. Теорема о площади треугольника.

30. Теорема синусов.

31. Теорема косинусов.

32. Решение треугольника по двум сторонам и углу между ними.

33. Решение треугольника по стороне и прилежащим к ней углам.

34. Решение треугольника по трем сторонам.

35. Скалярное произведение векторов. Определение.

36. В каком случае скалярное произведение ненулевых векторов равно нулю.

37. Скалярный квадрат вектора.

38. Формула скалярного произведения векторов.

39. Формула косинуса угла  между ненулевыми векторами.

40. Правильный многоугольник. Определение.

41. Сумма углов правильного n-угольника.

42. Теорема об окружности, описанной около правильного многоугольника.

43. Теорема об окружности, вписанной в правильный многоугольник.

44. Следствия теоремы об окружности, вписанной в правильный многоугольник.

45. Формула для вычисления площади правильного n-угольника.

46. Формула для вычисления стороны правильного n-угольника.

47. Формула для вычисления радиуса окружности, вписанной в правильный n-угольник.

48. Таблица «Правильные многоугольники».

49. Формула для вычисления длины окружности.

50. Формула для вычисления длины дуги окружности.

51. Формула для вычисления площади круга.

52. Круговой сектор.

53. Дуга кругового сектора.

54. Площадь кругового сектора.

55. Осевая симметрия.

56. Центральная симметрия.

57. Движение плоскости.

58. Наложение.

59. Параллельный перенос.

60. Поворот.

Лист ответов №3

1. Отрезок, для которого указано, какой из его концом считается началом, а какой - концом называется направленным отрезком или вектором.

2. Начало нулевого вектора совпадает с его концом, на рисунке нулевой вектор изображается одной точкой. Длина нулевого вектора равна нулю.

3. Длиной или модулем ненулевого вектора 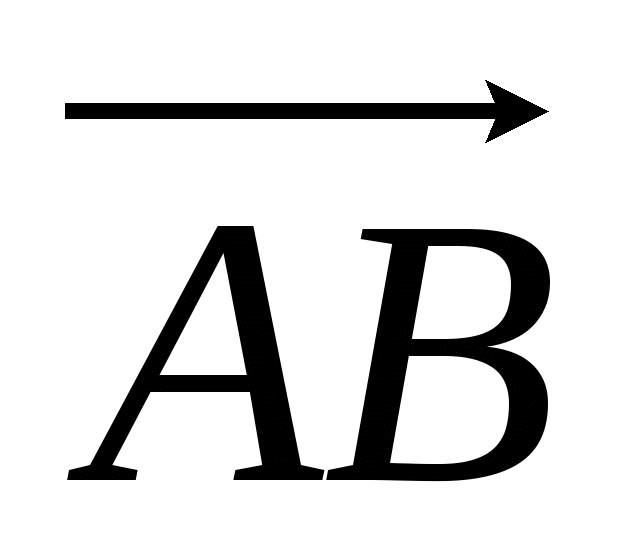называется длина отрезка AB.

4. Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.

5. Коллинеарные векторы делятся на сонаправленные и противоположно направленные. Два ненулевых вектора, называются сонаправллеными, если они коллинеарны и одинаково направлены. Два ненулевых вектора, называются противоположно направленными, если они коллинеарны и противоположно направлены.

6. Векторы называются равными, если они сонаправлены и их длины равны.

7. От любой точки можно отложить вектор, равный данному вектору, и притом только один.

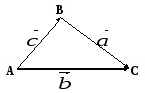
8. Правило треугольника

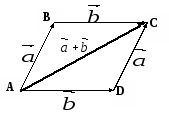
9. Правило параллелограмма

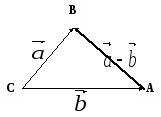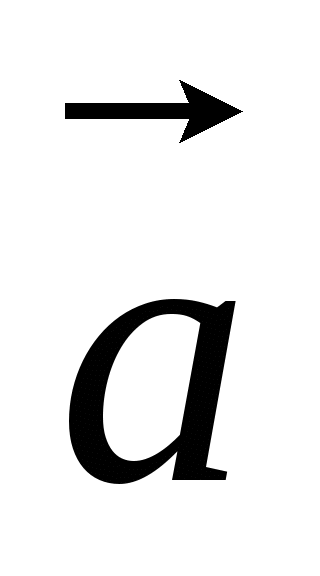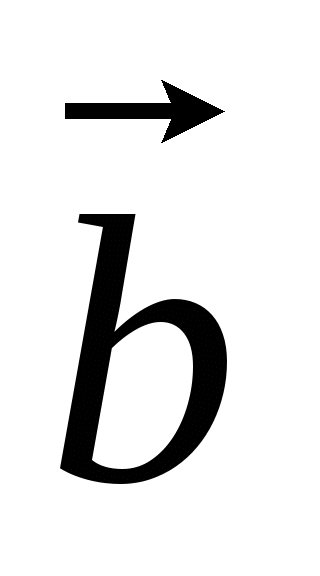10. Разностью векторов и называется такой вектор, сумма которого с вектором 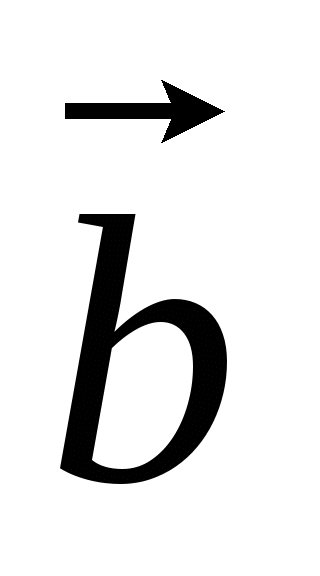равна вектору .

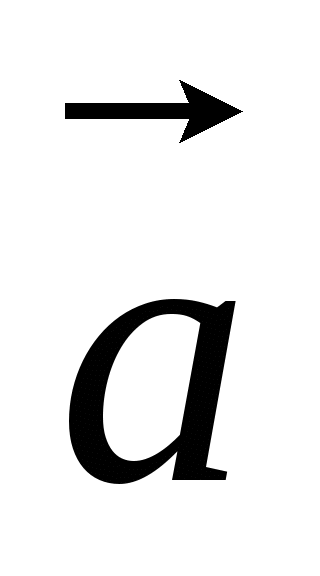11. Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

12. Средняя линия трапеции параллельна основаниям и равна их полусумме.

13. Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

14. Координаты равных векторов соответственно равны.

15. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

16. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

17. Каждая координата произведения векторов на число равна произведению соответствующей координаты вектора на это число.

18. Каждая координата вектора равна разности соответствующих координат его конца и начала.

Если А(х₁; у₁) и В(х₂; у₂), то

19. Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Если А(х₁; у₁) и В(х₂; у₂) и С - середина отрезка АВ, то С

20. Длина вектора равна квадратному корню из суммы квадратов его соответствующих координат.

Если ;, то .

21. Расстояние между двумя точками равно квадратному корню из суммы квадратов разности его соответствующих координат.

Если М₁(х₁; у₁) и М₂(х₂; у₂), то М₁М₂ = .

22. Уравнение окружности радиуса r c центром в точке С (х₀; у₀) имеет вид (x - x₀)² + (y - y₀)² = r². Уравнение окружности радиуса r c центром в начале координат имеет вид x² + y² = r².

23. Уравнение прямой имеет вид ax + by +c = 0.

24. Для любого угла α из промежутка 0⁰ ≤ α ≤ 180⁰ синусом угла α называется ордината 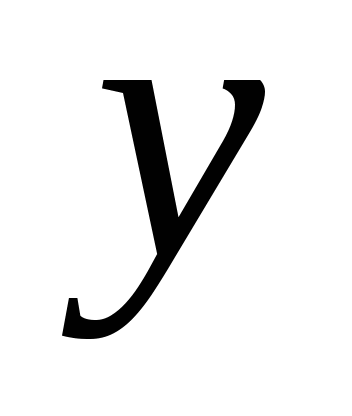точки M.

25. Для любого угла α из промежутка 0⁰ ≤ α ≤ 180⁰ косинусом угла α называется абсцисса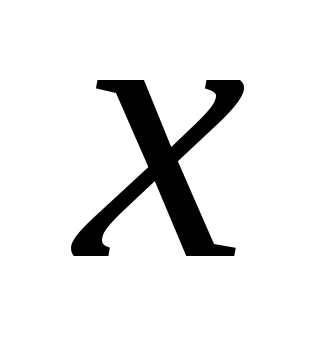точки M.

26. Тангенсом угла α (α ≠ 90⁰) называется отношение 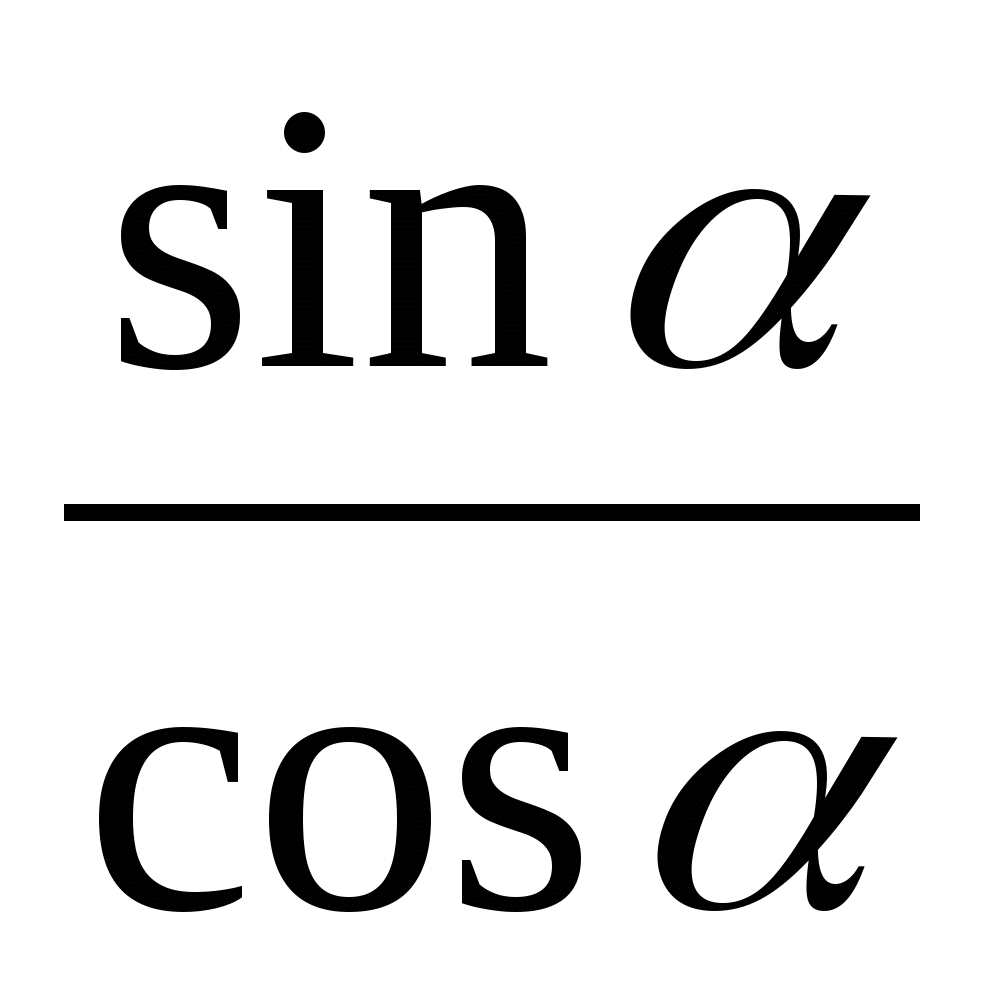, т. е. .

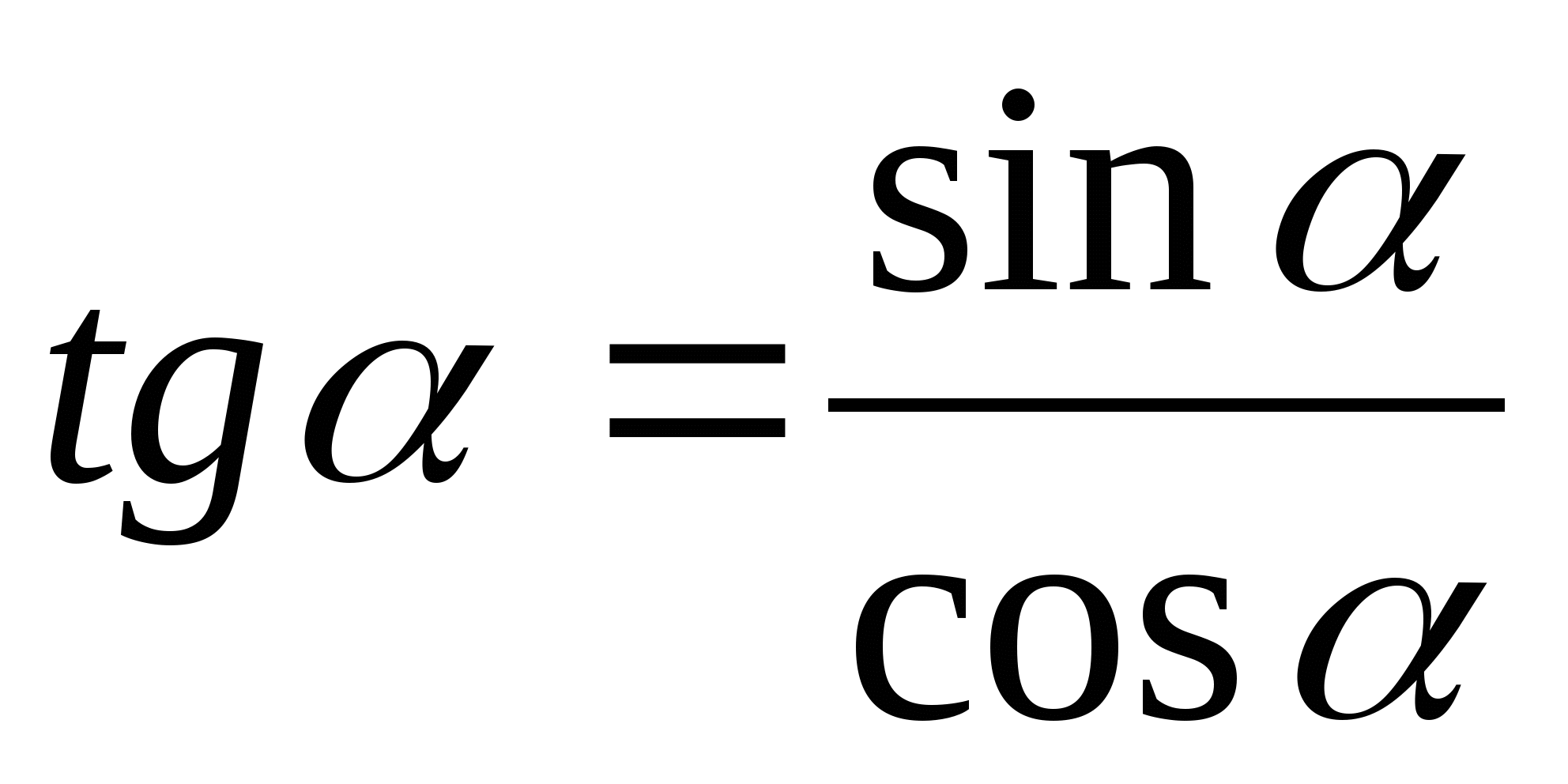27. Основное тригонометрическое тождество имеет вид sin² α + cos² α = 1.

28. Формулы приведения имеют вид

, при 0   90;

, при 0   180.

29. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

30. Стороны треугольника пропорциональны синусам противолежащих углов.

31. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

32. Ход решения треугольника по двум сторонам и углу между ними.

33. Ход решения треугольника по стороне и прилежащим к ней углам.

34. Ход решения треугольника по трем сторонам.

35. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

36. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

37. Скалярное произведение 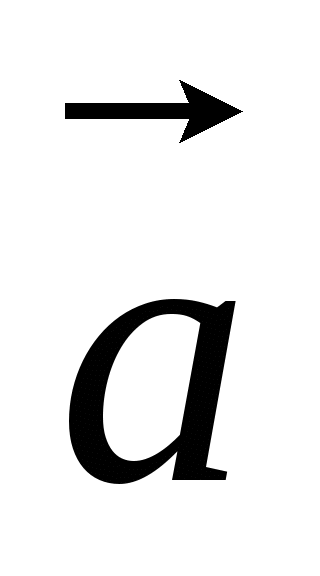∙ 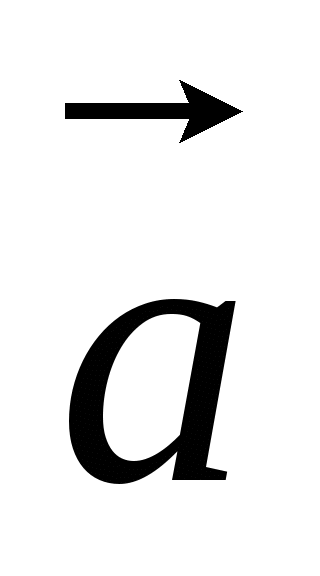называется скалярным квадратом вектора 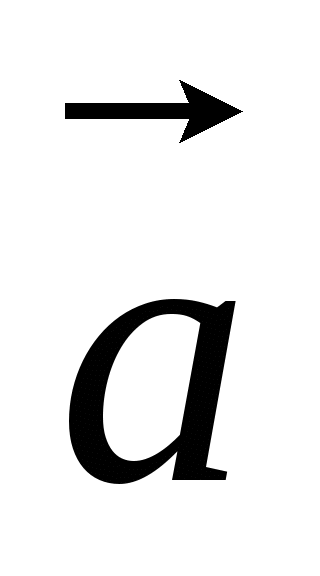и обозначается 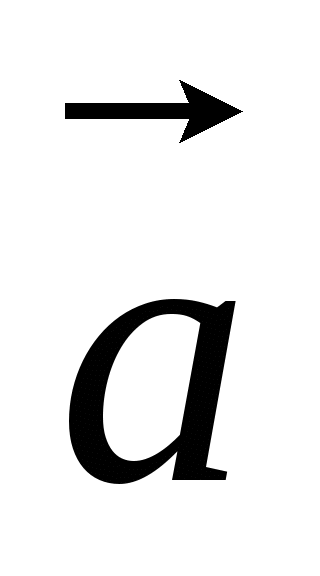² . Скалярный квадрат равен квадрату его длины.

38. Скалярное произведение векторов 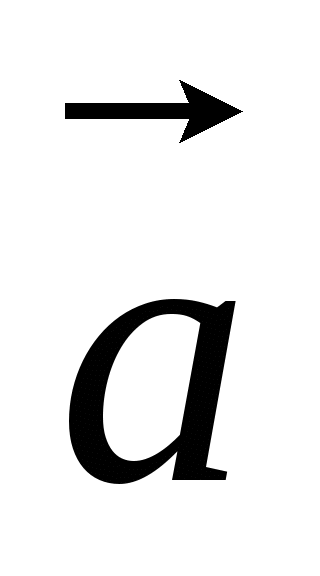{х₁; y₁} и 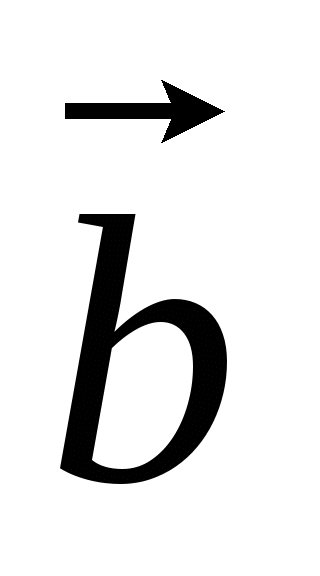{x₂ ; y₂} выражается формулой

∙ = x₁∙x₂ + y₁∙y₂.

39. Косинус угла α между ненулевыми векторами 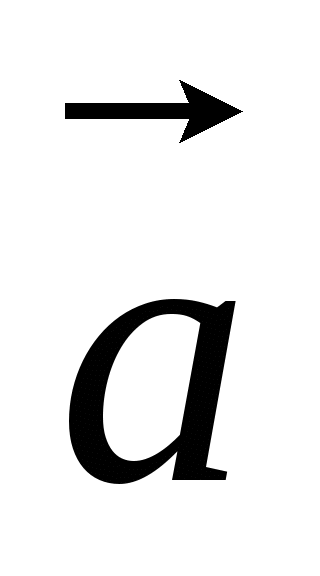{x₁ ; y₁} и 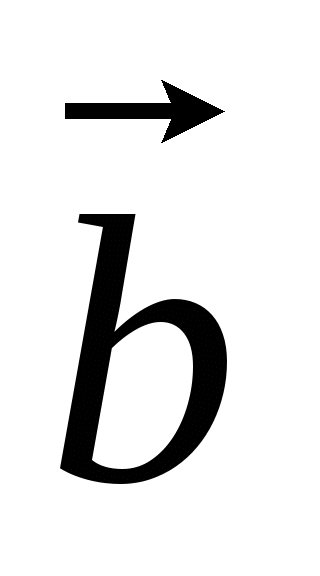{x₂ ; y₂} выражается формулой

x₁ ∙ x₂ + y₁ ∙ y₂

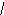
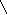
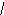
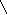cos α =

x₁²+y₁² ∙ x₂²+y₂²

40. Правильным многоугольником называется выпуклый многоугольник, у которого все углы и все стороны равны.

41. Сумма углов правильного n-угольника равна (n - 2)·180⁰.

42. Около любого правильного многоугольника можно описать окружность, и притом только одну.

43. В любой правильный многоугольник можно вписать окружность, и притом только одну.

44. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

45. Формула для вычисления площади правильного n-угольника.

S = , где Р - периметр правильного n-угольника, r - радиус окружности, описанной около правильного n-угольника.

46. Формула для вычисления стороны правильного n-угольника.

, где R - радиус окружности, вписанной в правильный n-угольник.

47. Формула для вычисления радиуса окружности, вписанной в правильный n-угольник.

r =

48. Таблица «Правильные многоугольники».

49. Формула для вычисления длины окружности. C = 2πR

50. Формула для вычисления длины дуги окружности. l =

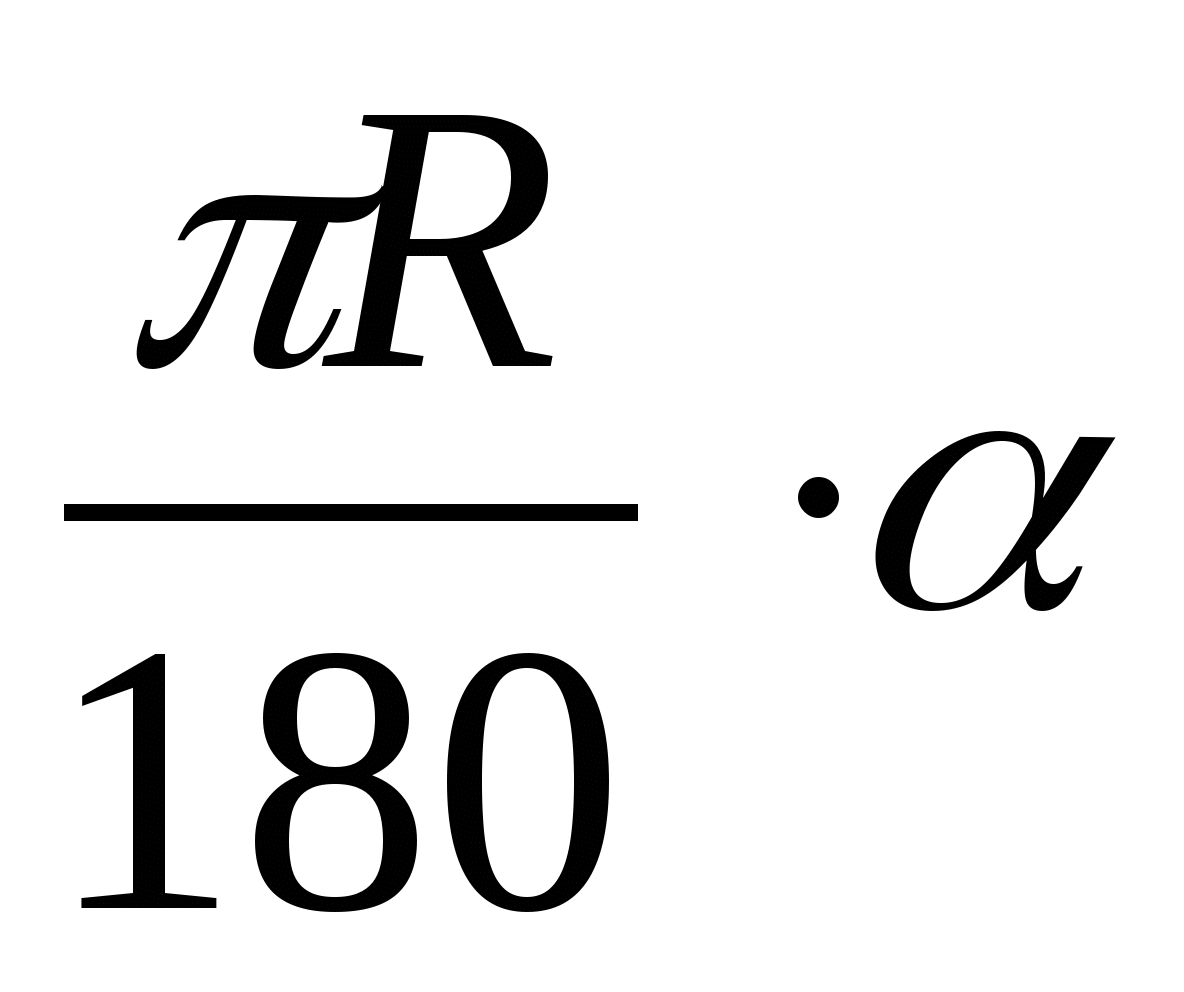
51. Формула для вычисления площади круга. S = πR²

52. Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

53. Дуга, которая ограничивает сектор, называется дугой сектора.

54. Площадь кругового сектора. S = .

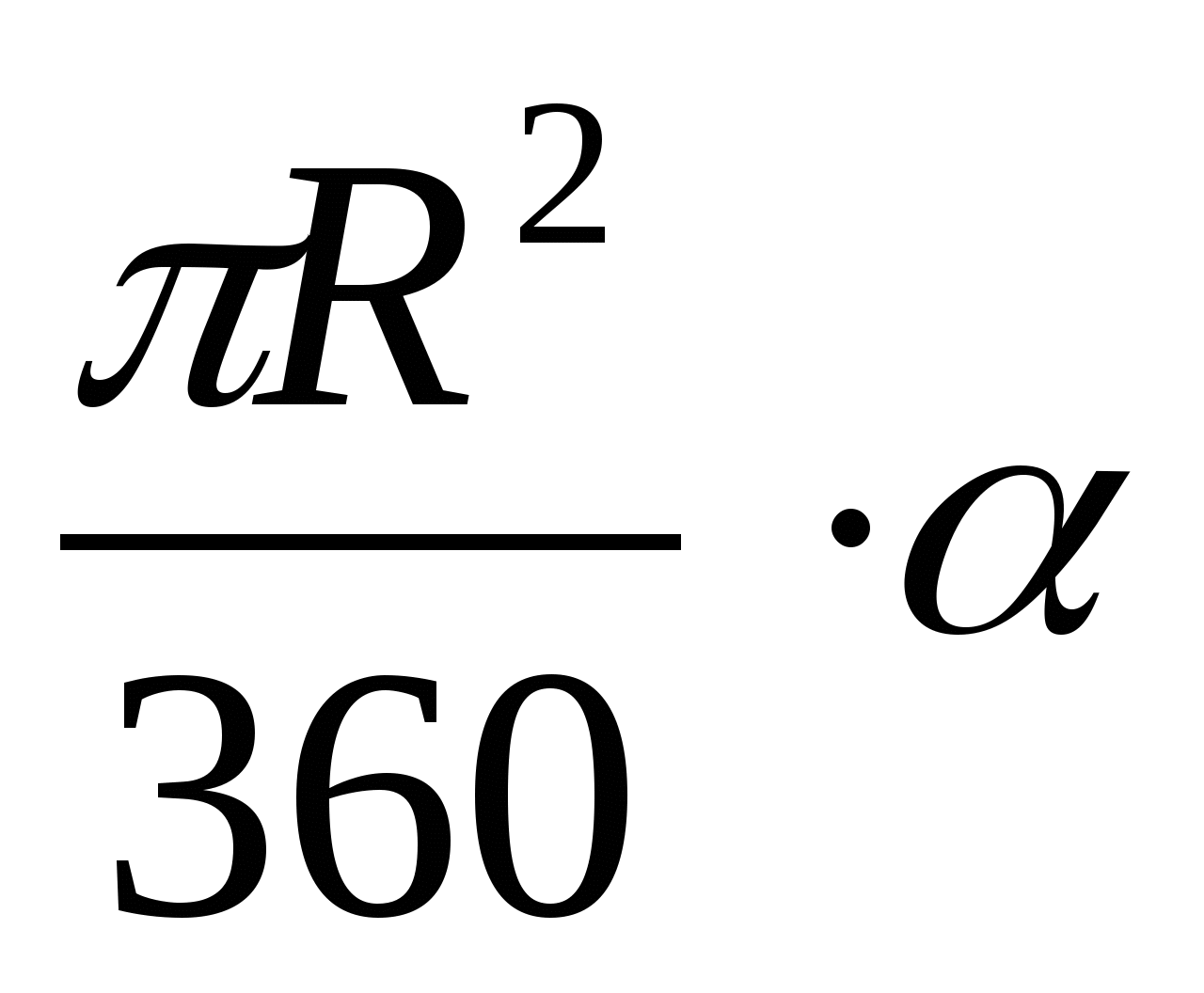55. Осевая симметрия представляет собой отображение плоскости на себя.

56. Центральная симметрия также является движением.

57. При движении отрезок отображается на отрезок. При движении треугольник отображается на равный ему треугольник.

58. Наложение - это отображение плоскости на себя. Любое движение является наложением. При движении любая фигура отображается на равную ей фигуру.

59. Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что вектор ММ₁ равен вектору а.

60. Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М₁, что ОМ = ОМ₁ и угол МОМ₁ равен α.