Координаты вектора. Решение задач с практическим содержанием

Конспект урока геометрии в 9-классе.

Тема урока «Координаты вектора. Решение задач с практическим содержанием».

Конспект урока разработан по учебнику геометрия 7 - 9 Л.С. Атанасян

Цели урока:

образовательная - повторение понятия «координаты вектора»;

совершенствование знаний и умений по теме «Нахождение координат вектора. Решение задач с практическим содержанием».

развивающая - продолжить: развитие логического мышления учащихся через использование ими специальных методов обучения (анализ, синтез, сравнение, обобщение, конкретизация, аналогия); математической речи (устной и письменной); развитие внимания.

воспитательная - продолжить: формирование коммуникативных умений, посредством использования групповой формы организации учебно-познавательной деятельности; формирование организационных умений; умений самоконтроля.

Оборудование: таблицы (файлы) со схемами поиска решения задачи; карточки-информаторы (подсказки различного уровня энтропии); таблицы с образцами записи решения задач (файлы); ТСО.

План проведения урока (этапы):

1. Организационный момент (1 мин)

2. Постановка цели урока (1 мин)

3. Устная работа (6 мин)

4. Групповая самостоятельная работа учащихся (25 мин)

5. Отчёты представителей групп (10 мин)

6. Постановка домашнего задания и подведение итогов урока (2 мин)

Ход урока

Этапы

Деятельность учителя

Деятельность учащихся

Реализация целей; замечания

I.

Приветствие и проверка общей готовности класса и учащихся к уроку (т.к. форма организации деятельности известна учащимся на перемене, то ученики сразу рассаживаются для работы в группах однородного и смешанного состава - по желанию учеников).

Приветствуют учителя, контролируют собственную готовность (на партах - тетради, учебники, ручки, карандаши, линейки, дневники).

формирование организованности в учении

II.

Цель урока: «На прошлом уроке мы все вместе учились решать задачи. На этом уроке, проведем устную работу, затем, работая в группах, мы продолжим эту работу с большей вашей самостоятельностью, и проверим, как вы умеете применять изученную теорию и способы учебной деятельности при решении задач. Запишите тему урока».

П

Решение задач по теме «Координаты вектора».ринимают цель урока и записывают тему:

В рамочке указаны записи, которые ученики выполняют в тетради

III.

Устная работа

Продолжите фразу:

1. Координатами вектора называется …

2. Теорема о разложении вектора по координатным векторам заключается в том, что …

3. При сложении двух векторов их координаты …

4. Длина вектора выражается …

5. Координатными векторами называются …

6. Вектор имеет координаты (x, y) тогда и только тогда …

7. При умножении вектора на число его …

8. Длина вектора AA2 , где A1(x1, y1), A2(x2, y2) выражается

- читают вопрос, дают ответ.

- поднимают руки; желающий ученик отвечает с места или выходит к доске и готовится рассказать решение задачи. - даётся перечень определений понятий и теорем, даются формулировки некоторых теорем;

- даётся перечень определений понятий и теорем;

- ученик у доски рассказывает идею решения задачи (использует схему поиска).

1) развитие устной речи;

2) сравнение;

3) самоконтроль

1) Ответы на вопросы могут быть даны в письменном виде.

2) Задачи можно проверить с помощью проектора

IY.

- раздаёт задания для групповой работы (уровень сложности задач указан в баллах от 3 до 5): задачи - приложение 1; лист контроля - приложение 4;

- указывает время для решения задач, фиксируется минимум задач, которые необходимо решить, максимум - не нормируется;

- контролирует деятельность учащихся, оказывается им (при необходимости) дифференцированная помощь (карточки информаторы) - приложение 2;

- контролирует выбор задач для выступления (задачи высокого и среднего уровней должны быть представлены в ответах учеников у доски)

- организует выступления учащихся у доски (по возможности целесообразно использовать проектор или готовые записи на доске, при условии, что у учеников есть свои, не очень аккуратные решения задач);

- собирает работы учеников, листы контроля каждой группы.

- приступают к выполнению заданий под руководством старшего по группе, который распределяет задачи по учащимся (1 задача на ученика), учитывая их возможности и собственный выбор;

- решают задачи, рассказывают решение своих задач товарищам по группе; оформляют решение своей (или одной другой) задачи на листке для предъявления учителю на проверку

- выбирают одну из задач для отчёта у доски;

- представители групп готовятся к выступлению, остальные подводят итоги работы в группе, выполняют взаимооценку, заполняют лист контроля.

анализ, синтез при поиске решения задач; конкретизация при обосновании решения;

формирование организованности в учении (выбор цели планирование, реализация, принятие решения о помощи, самоконтроль и взаимоконтроль)

Y.

Контролирует отчёты представителей групп, комментирует ответы, задаёт вопросы (приложение 5)

Представители групп выступают, остальные ученики слушают и (или) проверяют решение.

Развитие устной речи, внимания

YI.

Оценивает работу групп и класса в целом, сообщает домашнее задание (приложение 3)

Ученики слушают (и задумываются о процессе собственной деятельности).

Приложение 1 а). Задачи для групп однородного (сильного состава) состава.

З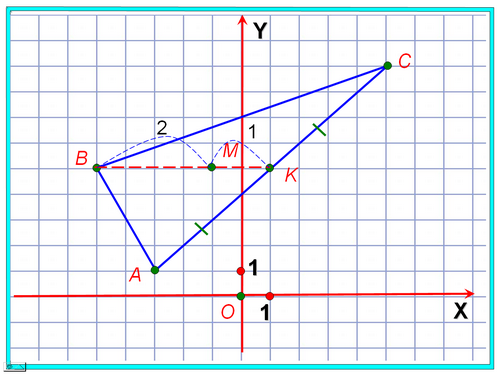адача 1. Определите расстояние между пунктом O и недоступной точкой M, если известны расстояния (в км.) OA, OB и OC, где A, B, C - пункты, расположенные в вершинах треугольника, центроидом которого является точка M. Точки имеют следующие координаты: O (0, 0),

A (-3, 1), B (-5, 5), C (5, 9).

Учащиеся на местах рисуют условие задачи на координатной плоскости.

Каким свойством обладает точка- центроид треугольника?

Где находится точка К?

Как найти ее координаты?

Приложение 2 а) подсказки разного уровня:

Подсказка последнего уровня: Подсказка 4-го уровня:

1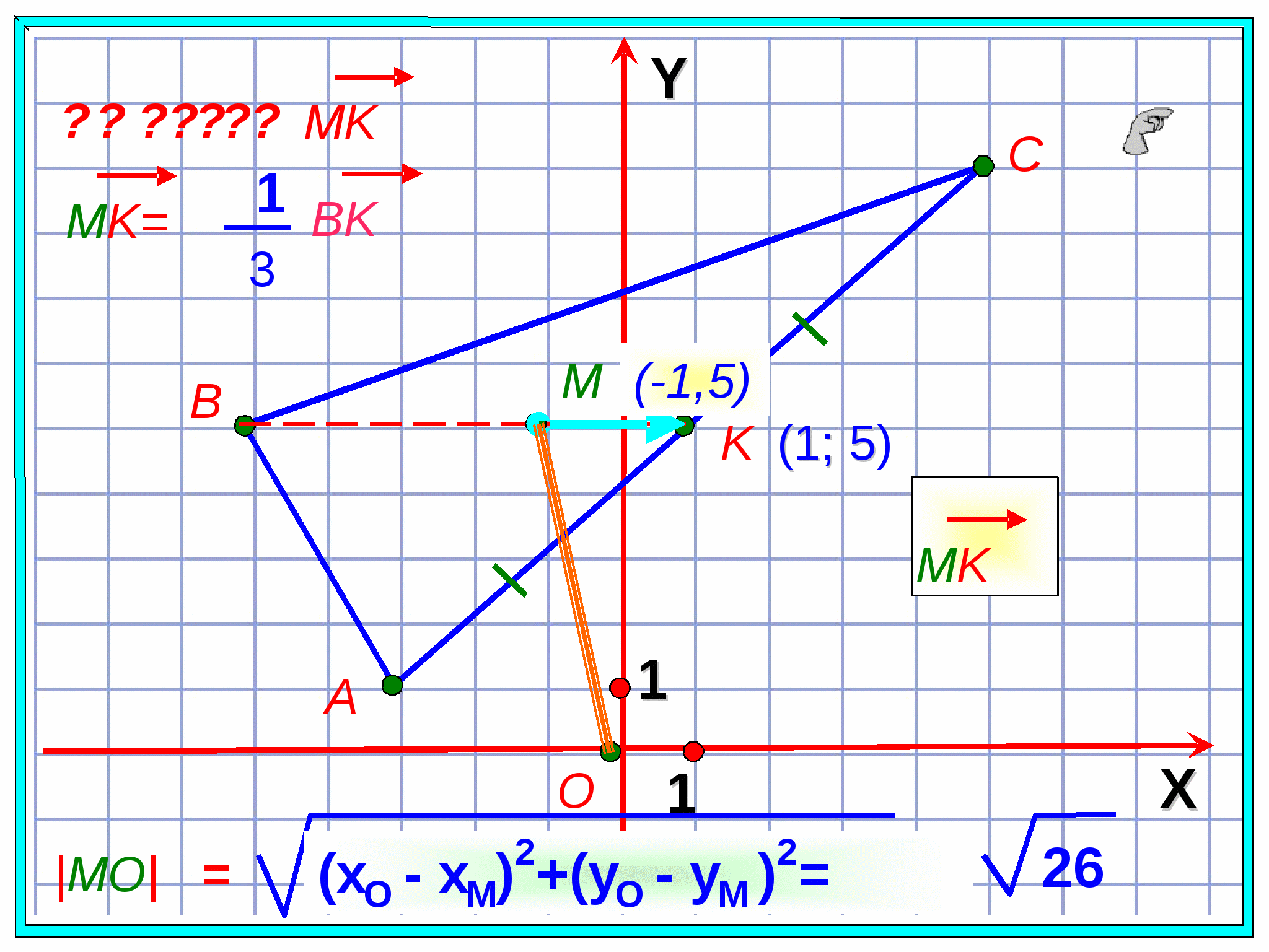. Найдем координаты точки К - середины АС.

2. Выразим МК =1/3 ВК.

3. Вычислим MO|=√(xO - xM)² +(yO - yM )².

Приложение 1 б). Задачи для групп однородного (слабого) состава:

Задача 1. Даны точки А (0, 1), В (1, 0), С (1, 2), D (2, 1). Докажите равенство векторов АВ и СD.

Приложение 2 б). Подсказки разного уровня:

Подсказка 1-го уровня

Подсказка 2-го уровня:

1. Вспомнить определение вектора.

2. Вспомнить формулу координат вектора.

3. Изобразить равные векторы.

4. Записать формулы и найти координаты векторов, сравнить, сделать вывод.

Подсказка 3-го уровня:

1. Найти в учебнике определение вектора.

2. Найти в учебнике формулу координат вектора.

3. Используя данный чертёж, записать формулу, найти координаты вектора АВ.

4. Аналогично - для найти координаты вектора СD.

Приложение 2. Домашнее задание.

Задача 1. В прямоугольной системе координат паучок сплел паутину, ожидая обед в ее центре. В его сети попались: Бабочка (3;8), Муха (-4;5) и комар (?;?).

Найдите:

1. Координаты комара, зная что:

- Комар находится в нечетной четверти от бабочки;

- Паучок сидит на середине отрезка БК;

2. Расстояние МБ;

3. Периметр треугольника МБК;

4. Середины отрезков БК; КМ; МБ.

Задача 2. Лестница, стоящая на гладком полу у стены соскальзывает вниз. По какой линии движется котенок, сидящий на середине лестницы? Котенка примите за единичный вектор.

Задача 3. В квадрат вписана окружность. Доказать, что сумма квадратов расстояний любой точки окружности до сторон квадрата постоянна.

Приложение 3. Лист контроля

Приложение 4. Вопросы к учащимся в процессе отчётов представителей групп (эти вопросы можно использовать, как задание для рефлексии, выполненной в письменном виде дома за подписью родителей).

1. Какие теоремы, свойства и формулы Вы использовали при решении задачи?

2. Какие затруднения у Вас возникли в процессе решения задач?

3. Какая из задач вам показалась наиболее трудной?

4. Пользовались ли Вы учебником, словарём?

5. Довольны ли Вы результатом своей деятельности? Почему?

6. Как Вы считаете, продолжилось ли Ваше умственное развитие при решении задач? Почему?

7. Что помешало Вам добиться лучших результатов?

8. Какие выводы Вы сделаете для себя после этой работы?