- Учителю
- 6 Сыныптың математика пәнінен 'Екі айнымалысы бар сызықтық теңдеулер жүйесін шешу' сабақ жоспары
6 Сыныптың математика пәнінен 'Екі айнымалысы бар сызықтық теңдеулер жүйесін шешу' сабақ жоспары






 Сынып: 6
Сынып: 6
Күні:
Тақырыбы: «Екі айнымалысы бар сызықтық теңдеулер жүйесін қосу, алмастыру және графиктік тәсілмен шешу»
I.Сабақтың мақсаты:
Білімділік: Оқушылардың коммуникативті және проблемаларды шешу құзыреттіліктерін қалыптастыру, берілген материалды түсініп оқу және түсініп тындау дағдыларын қалыптастыру
Дамытушылық: Логикалық ойлау қабілеті мен есептеу дағдыларын жетілдіру, өз бетінше еңбектену, белсенділіктерін арттыру, пәнге қызуғушылығын ояту
Тәрбиелік: Оқушыларды ұқыптылыққа, бір - біріне сыйластыққа тәрбиелеу.
II. Сабақтың көрнекіліктері: Түрлі түсті маркерлер, интербелсенді тақта, карточкалар
III. Сабақтың әдісі: Диалогтік оқыту, АКТ, топтық жұмыс, жұптық жұмыс, бағалау,
IV. Сабақтың барысы:
1) Ұйымдастыру кезеңі: а) Сәлемдесу. Кезекшінің мәліметі.
ә) Топта психологиялық жағдай орнату.(2 мин)
2) Үй тапсырмасын тексеру:
3)ӨЖ карточкалары бойынша теориялық білімдерін тексеру.(2 мин)
4)математикалық диктант (АҚТ- ны қолданып,АctivInspire) (3 мин)
V. Жаңа тақырып:
Тексеру таблосы
№
Оқушының аты-жөні
ӨЖ
Математикалық диктант
ТӨА
ПТ
Бақылау кезеңі
Рефлексия
1
Бекжан С
ӨЖ-1
Бірін бірі тксеру
ТӨА - 1
Оқытады Калтаева А
ПТ-2
Тест
2
Калтаева А
ӨЖ-2
ТӨА - 2 оқытады Бекжан С
ПТ-1
Тест
3
Мағзұм Қ
ӨЖ-3
ТӨА- 3 оқытады Хуатбек Х
ПТ-4
Тест
4
Хуатбек Х
ӨЖ-4
ТӨА - 1оқытады Мағзұм Қ
ПТ-3
Тест
А) Тақырыптармен өзара алмасу - 5 мин
Ә) Практикалық тапсырмалар - білімдерін жинақтау мақсатында деңгейлік тапсырмаларды орындау. - 20 мин
Б)Бақылау кезеңі - тест жұмысы (10 мин) интербелсенді тақта Power Paint
VI. Қорытындылау кезеңі - 3 мин
-Рефлексия -
Мен білемін
Нені білмеймін
Нені білгім келеді
-Үй жұмысын хабарлау
-Өзін - өзі бағалау - рейтинг парағы
ӨЖ-1
1.Координаталық жазықтық дегеніміз не?
Координаталар жүйесі бар жазықтық координаталық жазықтық деп аталады
2.Масштаб дегеніміз
Картада берілген арақашықтықтың нақты арақашықтыққа сәйкестігін М=Н:К
3.Рационал сандарды салыстыру
-кез келген оң рационал сан нөлден үлкен
-кез келген теріс рационал сан нөлден кіші
-Кез келген оң сан теріс саннан үлкен
-екі теріс санның модулі ұлкені модулі кішісінен кіші
ӨЖ-2
1.Пропорция дегеніміз
Екі немес бірнеше қатынастардың теңдігі
2.Сызықтық функцияның графигі
Түзу сызық
3.Қарама-қарсы сандар дегеніміз
Бір-бірінен таңбасымен өзгешеленетін сандар
ӨЖ-3
1.Параллель түзулер дегеніміз
Бір жазыөтыөта жататын және қиылыспайтын екі түзуді параллель түзулер деп атайды
2.Дөңгелектің ауданынын формуласы
S=nR2
3.Жұп және тақ сандар
Жұп сандар 0,2,4,6,8 цифрларымен аяқталатын сандар жұп сандар, ал 1,3,5,7,9 цифрларымен аяқталатын сандар тақ сандар деп аталады
ӨЖ-4
1.Нүктеден түзуге дейінгі қашықтық деп..
Берілген нүктеден түзуге дейін жүргізілген перпиндикуляр
2.Оң және теріс сандар
Координаталық түзуде оң жағындағы сандар оң, ал сол жағындағы сандар теріс деп аталады
3.2-ге, 5-ке және 10-ға бөлінгіштік қасиеті
2-ге жұп сандар, 5-ке о және 5 цифрларымен аяқталған сандар, 10-ға 0 цифрымен аяқталған сандар
ТӨА - 1
Тақырып: Екі айнымалысы бар сызықтық теңдеулер жүйсін қосу тәсілімен шешу
Мақсаты: Екі айнымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен шешу алгоритмімен таныстыру және екі айнымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен шешу дағдыларын қалыптастыру.
1.Берілген теңдеулер жүйесін шеш
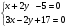
Алгоритм:
1.Бұл теңдеулер жүйесіндегі теңдеулердің құрамындағы 2у және -2у қосындысы 0-ді береді. Демек
х+2у-5=0
+ 3х-2у+17=0
4х+12=0
2. Шыққан теңдеудің түбірін табамыз
4х+12=0
4x=-12
x=-3
3. Шыққан х-тің мәнін, теңдеулердегі х-тің орнына апарып мәнін қойып, у-ті табамыз.
Х+2у-5=0
-3+2у-5=0
2у=8
У=4
Жауабы (-3;4)
II. Берілген теңдеулер жүйесін қосу тәсілімен шеш
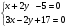
ТӨА - 2
Тақырып: Екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу
Мақсаты: Екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу алгоритмімен таныстыру және екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу дағдыларын қалыптастыру.
I.Берілген теңдеулер жүйесін шеш
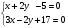
Алгоритм:
1.Бірінші теңдеугі х айнымалысын у арқылы өрнектейміз, екінші теңдеудені х-тің орнына қоямыз.
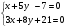
2.екінші теңдеуді шығарамыз
21-15у+8у+21=0
-7y=-42
y=6
3. 6 санын бірінші теңдеудегі у-тің орнына қоямыз
Х=7-5*6=-23
Жауабы (-23;6)
II. Берілген теңдеулер жүйесін алмастыру тәсілімен шеш
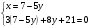
ТӨА - 3
Тақырып: Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу
Мақсаты: Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілімен шешу алгоритмімен таныстыру және екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілімен шешу дағдыларын қалыптастыру.
1.Берілген теңдеулер жүйесін шеш
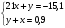
Алгоритм:
1.Әрбір теңдеугі у-ті х арқылы өрнектейміз:
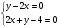
2. Берілген жүйедегі теңдеулердің графиктерін бір координаттар жүйесінде сызымаз, қиылысу нүктесін табамыз.
У=2x y=-2x+4
X
0
1
Y
0
2
X
0
1
Y
4
2
2 А
1
3.Берліген графиктердің қиылысуы (1;2)
II. Берілген теңдеулер жүйесін графиктіктік тәсілмен шешу
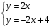
ТӨА - 4
Тақырып: Екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу
Мақсаты: Екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу алгоритмімен таныстыру және екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу дағдыларын қалыптастыру.
I.Берілген теңдеулер жүйесін шеш
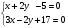
Алгоритм:
1.Бірінші теңдеугі х айнымалысын у арқылы өрнектейміз, екінші теңдеудені х-тің орнына қоямыз.
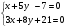
2.екінші теңдеуді шығарамыз
21-15у+8у+21=0
-7y=-42
y=6
3. 6 санын бірінші теңдеудегі у-тің орнына қоямыз
Х=7-5*6=-23
Жауабы (-23;6)
II. Берілген теңдеулер жүйесін алмастыру тәсілімен шеш
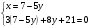
ПТ - 1
I. Берілген теңдеулер жүйесін шеш
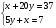
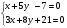
II.Теңдеулер жүйесін шеш
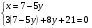
III.Егер 2007 жылға қарағанда 2006 жылы республикамызда 392014 кг кем қант, ал осы екі жылда барлығы 392508 т қант өндірілсе, онда әр жылда қанша тонна қант өндірілген?
ПТ - 2
I. Берілген теңдеулер жүйесін шеш
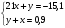
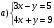
II.Теңдеулер жүйесін шеш
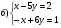
III.Елімізде а жылы картоп егістігінің ауданы көкөніс егістігінің ауданынан b мың га-ға артық, ал көкөніс пен дәнді дақылдар себілген аудан c мың га болды. Егер дәнді дақылдар ауданы картоп егістігінің ауданына d мың га-ға артық болса, онда көкөніс, картоп және дәнді дақылдар егістігінің ауданын табыңдар?Мұндағы a= 2003, b=56,7 c=13982,8 ;d=13705,7
ПТ - 3
I. Берілген теңдеулер жүйесін шеш
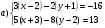
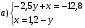
II.Егер А (x;y) нүктесі
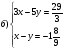
Теңдеулер жүйесінің шешімі болса, онда 7х+3у өрнегінің мәнін табыңдар
III.2008 жылы Қарағанды облысы мен Қостанай облысы әрбір гектардан 467 ц көкөніс жинаған. Қарағанды облысының әрбір 1га-дан жинаған өнімі Ұостанай облысының 4га-дан жинаған өнімінен 548 ц кем. 2008 жылы әрбір облыс бір гектардан қанша центнерден көкөніс жинаған?
ПТ - 4
I. Берілген теңдеулер жүйесін шеш
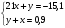
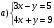
II.Теңдеулер жүйесін шеш
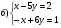
III.Елімізде а жылы картоп егістігінің ауданы көкөніс егістігінің ауданынан b мың га-ға артық, ал көкөніс пен дәнді дақылдар себілген аудан c мың га болды. Егер дәнді дақылдар ауданы картоп егістігінің ауданына d мың га-ға артық болса, онда көкөніс, картоп және дәнді дақылдар егістігінің ауданын табыңдар?Мұндағы a= 2003, b=56,7 c=13982,8 ;d=13705,7
Бағалау парағы
Оқушының аты-жөні_____________________________________________
Тақырып________________________________________________________
№
Критерийлер
1ұпай алгоритмін дұрыс қолданбаса
2ұпай-алгоритмін дұрыс қолданды,бірақ қате жіберді
3 ұпай-қатесіз
Жалпы ұпай
1
ӨЖ карточкасы
2
Математикалық диктант
3
ТӨА
4
ПТ
5
Тест жұмысы
«5»- 12-15 ұпай
«4» -11-9 ұпай
«3»- 5-8 ұпай
Стандартты меңгеру мониторингі:
Оқушының аты-жөні
Екі айнымалысы бар теңдеулер жүйесін қосу тәсілімен шешу
Екі айнымалысы бар теңдеулер жүйесін алмастыру тәсілімен шешу
Екі айнымалысы бар теңдеулер жүйесін графиктік тәсілімен шешу
Бекжан С
Калтаева А
Мағзұм Қ
Хуатбек Х
Күні
Екі айнымалысы бар теңдеулер жүйесін қосу тәсілімен шешу
Екі айнымалысы бар теңдеулер жүйесін алмастыру тәсілімен шешу
Екі айнымалысы бар теңдеулер жүйесін графиктіктәсілімен шешу
100%
…
20%
10%
0%
б/ж өткізу күні