- Учителю
- Мастер-класс по теме Различные способы решений задач повышенной сложности (С5) при подготовке к ЕГЭ
Мастер-класс по теме Различные способы решений задач повышенной сложности (С5) при подготовке к ЕГЭ
Мастер-класс учителя математики МБОУ СОШ №8 г. Каменск-Шахтинского Семиглазовой Нины Ильиничны.
Различные способы решений задач повышенной сложности (С5) при подготовке к ЕГЭ
Найдите, при каких значениях параметра а данное уравнение
а (х+3)-а│х-4│=(8х-х2-10)•│х-4│-(8х-х2-10)(а+3) имеем ровно 2 корня.
Решение.
Преобразуем это уравнение.
а (а+3)-а│х-4│=(8х-х2-10)• │х-4│- (8х-х2-10) (а+3);
(а (а+3)+(8х-х2-10) (а+3))- │х-4│(а+8х-х2-10)=0
(а+8х-х2-10)(а+3 - │х-4│)=0
(х2-8х+10-а)( │х-4│-а-3)=0 - это уравнение должно иметь 2 корня.
х2-8х+10=а,
│х-4│-3=а.
Построим графики функций
у=х2-8х+10 и у=│х-4│-3
х0=4; х0=4
у0(4)=-6 у(4)=-3
по графику определяем, что данное уравнение имеет при -6<х<-3 и при условии
х2-8х+10 =│х-4│-3
х2-8х+16-16+10-│х-4│+3=0
(х-4)2-│х-4│- 3 =0
Пусть │х-4│=t; t≥0
t2- t-3=0
t1=![]()
t2=![]() - не удовлетворяет условию t≥0
- не удовлетворяет условию t≥0
t
 =
=![]() │х-4│=
│х-4│=![]() х1=
х1=![]() х2=4-
х2=4-![]()

Функция у=х2-8х+10 и у=│х-4│- 3 симметричны относительно прямой х=4
у(х1)=у(х2)
у(х2)=у (4-![]() )
)
│4-![]() -4│-3=│-
-4│-3=│-![]() │-3=
│-3=![]() -3=
-3=![]()
Следовательно, а =![]()
Ответ. (-3;-6)![]() {
{![]() }
}
II способ
Возможны следующие случаи:
1)Уравнение ![]() имеет 2 корня при этом уравнение
имеет 2 корня при этом уравнение ![]()
![]() корней не имеет:
корней не имеет:
![]()
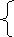
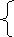
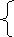
 >0
а+6>0 а>-6
>0
а+6>0 а>-6
а<-3 а<-3 -6<а<-3
а+3<0
2) Уравнение ![]()
![]() имеет 2 корня, а уравнение
имеет 2 корня, а уравнение ![]() корней не имеет.
корней не имеет.
![]()
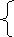
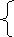
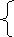
 <0
а+6<0 а<-6
<0
а+6<0 а<-6
а>-3 а>-3 система несовместна
а+3>0
3) Каждое уравнение имеет по одному корню и при этом корни разные.
![]()
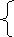
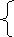
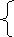
 =0
а+6=0 а=-6
=0
а+6=0 а=-6
а+3=0 а=-3 а=-3 система несовместна
4) Каждое уравнение имеет по 2 корня, но эти корни одинаковые:
х1![]() =
х1
=
х1![]()
![]()
х2![]() =
х2
=
х2![]()
![]()
при одинаковых значениях.
х2-8х+10-а=0 ![]() │х- 4│= а+3
│х- 4│= а+3
х1,2=4![]() х-4 = а+3 х - 4 = -а-3
х-4 = а+3 х - 4 = -а-3
х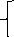
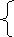 1
1![]() =4
=4![]() х1
х1![]()
![]() =а+7
х2
=а+7
х2![]() =1-а
=1-а
х2![]() =4
=4![]() а>-3 а>-3
а>-3 а>-3
Если а+7>1-а, то а>-3 - верно
2а>-6
а>-3
Если а+7<1-а, то а<-3 - неверно
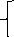
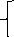 4+
4+![]() =а+7
=а+7
![]() =а+3
=а+3


![]() =а+3
=а+3
4-![]() =1-а
=1-а
![]() =3+а
=3+а
6+а=а2+6а+9
а2+5а+3=0
Д=13
![]()
![]()
а1<-3 а2>-3
не подходит
Ответ: -6<а<-3
а=![]()