Урок по алгебре на тему Линейная функция и ее график (7 класс)

Гнездилова Елена Александровна, учитель математики. МКОУ «СОШ № 8 имени А. В. Грязнова» Изобильненского муниципального района Ставропольского края.

</ Сценарий урока по алгебре «Линейная функция и ее график» предназначен для учителей математики. Урок направлен на изучение нового материала через включение учащихся в активную позицию.

Тема: «Линейная функция и ее график»

Тип урока: изучение нового материала.

Задачи: создать условия для развития умений определять является ли функция

, заданная формулой, линейной; строить график линейной функции.

Планируемые результаты

Предметные: ввести понятие линейной функции; формировать навык построения графика линейной функции.

Метапредметные: познавательные - ориентироваться на разнообразие способов решения задач;

регулятивные - учитывать правило в планировании и контроле способа решения;

коммуникативные - учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.

Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Оборудование: доска, мел, линейка.

Сценарий урока.

1. Организационный этап.

2. Этап актуализации знаний.

1. Является ли решением уравнения х - 3у = 1 пара чисел

1. (1; - 4);

2. (0 ; 3);

3. (- 1; - 4);

4. (2; 3);

5. (20; 3)?

2. Выразите переменную у через переменную х из уравнения

1. 2х + у = 5; б) 5х - у = 1; в) 6х + 2у = 10.

3. Выразите переменную х через переменную у из уравнения

1. х + у = 3; б) х + 3у = 5; в) 3х - 9у = 12.

3. Этап целеполагания.

- При построении графика линейного уравнения мы дважды решали уравнение относительно у. Математики это считают не рациональным и предложили выразить у из уравнения, и тогда легче будет проводить вычисления (а главное, быстрее).

Линейное уравнение с двумя переменными x и у в случае, когда b ≠ 0, можно преобразовать к виду , где k, m - числа (коэффициенты), k ≠ 0.

ax + by + c + 0;

by = - ax - c;

y = - x - .

Введя обозначения - k, - = m, получаем:

y = kx + m.

Это частный вид линейного уравнения. Зная, чему равен х, по правилу всегда можно найти, чему равен у. Это правило называют линейной функцией.

- Сформулируйте тему нашего урока.

- Какова цель нашего урока?

4. Этап изучения нового материала.

- Функция вида , где k, m - числа (коэффициенты), k ≠ 0 называется линейной.

х - аргумент (независимая переменная).

у - функция (зависимая переменная).

Функция задается:

1. Формулой: .

2. Парами чисел: (х₁; у₁) и (х₂; у₂).

3. Таблицей:Графиком.

   - Что является графиком линейной функции?

   -Графиком функции вида является прямая.

   - Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая.

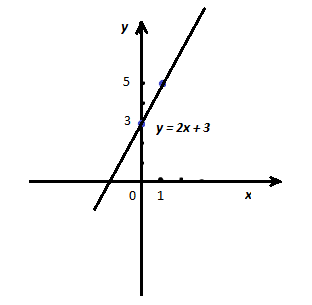
   - Построим график функции , где k = 2, а m = 3.

   - Так как графиком линейной функции является прямая, нам достаточно иметь две точки.

   х- независимая переменная, значит ее значения выберем сами.

   у - зависимая переменная, ее значения найдем в результате подстановки выбранного значения х в функцию.

   Результаты запишем в таблицуЕсли х = 0, то у = 2 ∙ 0 + 3 = 3.

   Если х = 1, то у = 2 ∙ 1 + 3 = 5.

   Точки (0; 3) и (1; 5) отметим на координатной прямой и проведем через них прямую.

   

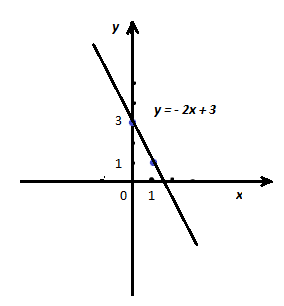
   - Построим график функции , где k = - 2, а m = 3.(Один ученик у доски, остальные в тетрадях)

   Составим таблицуПостроим на координатной плоскости точки (0; 3) и (1; 1) и проведем через них прямую.

   

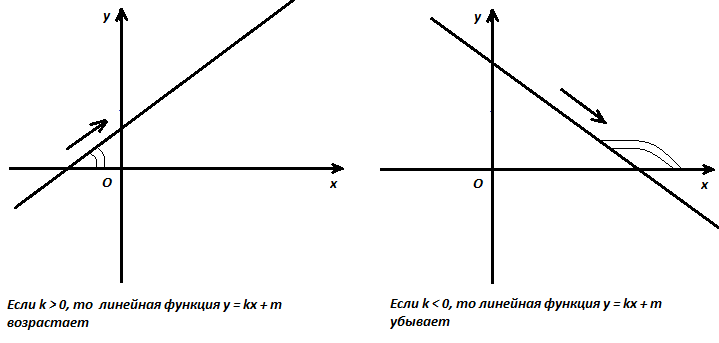
   Мы построили два графика, определите взаимосвязь коэффициентов и расположения прямых.

   

   5. Этап закрепления нового материала.

   № 8.4(а. б)

   № 8. 6 - 8.7 (устно)

   № 8.8 (а, б)

   № 8.10 (а, б)

   № 8.15 (а, б)

   № 8. 16(а, б)

   № 8. 17(а, б)

   6. Итоги урока.

   - Функция какого вида называется линейной?

   - Что является графиком функции

   - Сколько точек необходимо для построения графика функции ?

   - Что показывает коэффициент k?

   7. Рефлексия.

   8. Домашнее задание.

   № 8.15 (а, б)

   № 8. 16(а, б)

   № 8. 17(а, б)