Урок Решение задач по теме Треугольники

Решение задач «Треугольники»

Цели и задачи урока:

образовательные:

• обобщить, закрепить и углубить знания по изученной теме;

• формировать умение обучаемых доказывать равенство данных треугольников, опираясь на изученные признаки, применять свойства равнобедренного треугольника;

• отработать навыки решения простейших задач на построение с помощью циркуля и линейки;

развивающие:

• развивать логическое мышление, самостоятельность учащихся при решении заданий; умение на практике применять знания, полученные на уроках;

воспитывающие:

• воспитывать познавательную активность, упорство в достижении поставленной цели, культуру умственного труда

Оборудование:

• наглядный материал (готовые чертежи);

• карточки с задачами для индивидуальной работы на доске;

• таблицы с признаками равенства треугольников.

Тип урока: урок закрепления полученных знаний.

Ход урока

І. Организационный момент.

Учитель:

- Тема урока: «Решение задач по теме «Треугольники»». Мы сегодня обобщим и систематизируем знания по данной теме и наша цель: подготовиться к контрольной работе, которая будет на следующем уроке.

- Откройте дневники и запишите домашнее задание.

- Обратите внимание:

• I уровень: № 120(б), 121;

• II - III уровень: №160 (б), 162(б).

II. Актуализация опорных знаний.

1. У доски двое учащихся решают задачи по карточкам.Карточка № 1.

Начертите равнобедренный треугольник АВС с основанием АС. С помощью циркуля и линейки проведите медиану АА1 к боковой стороне ВС.

Карточка № 2.

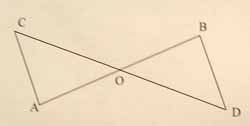
Дано: АО = BO, СО = DO, CO = 5см, ВО = 3см, BD = 4см.

1)Докажите, что САО = DBO.

2)Найдите периметр треугольника САО.

2. Для остальных учащихся класса организована фронтальная работа.

Цель: повторить основные вопросы теории темы «Равнобедренный треугольник и его свойства» с помощью теста.

Теоретический тест. [1]

1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:

а) всегда верно;

б) может быть верно;

в) всегда неверно.

Ответ: б), если медиана проведена к основанию равнобедренного треугольника.

2) Если треугольник равносторонний, то:

а) он равнобедренный;

б) все его углы равны;

в) любая его высота является биссектрисой и медианой.

Ответ: а), б), и в), равносторонний треугольник является частным случаем равнобедренного треугольника; в равнобедренном треугольнике углы при основании равны, поэтому в равностороннем треугольнике все углы равны.

3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника?

а) в любом;

б) в равнобедренном;

в) в равностороннем.

Ответ: б), высота, проведённая к основанию равнобедренного треугольника.

4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:

а) всегда верно;

б) может быть верно;

в) всегда неверно.

Ответ: а)

5) Если треугольник равнобедренный, то

а) он равносторонний;

б) любая его медиана является биссектрисой и высотой;

в) ответы а) и б) неверны.

Ответ: в), т.к. равнобедренный треугольник не всегда является равносторонним; медиана, проведённая к боковой стороне равнобедренного треугольника, не является биссектрисой и высотой, если треугольник не равносторонний.

6) В каком треугольнике любая его высота делит треугольник на два равных треугольника?

а) в любом;

б) в равнобедренном;

в) в равностороннем.

Ответ: в).

Проверка ответов.

Учитель:

- Мы с вами повторили материал темы «Равнобедренный треугольник и его свойства», а теперь повторим признаки равенства треугольников. (Обратить внимание обучающихся на таблицы с признаками равенства треугольников)



3. Задачи в рисунках (на доске).

Учитель:

- Определите, являются ли равными треугольники на рисунках.

- Сколько пар равных элементов должно быть в равных треугольниках?

Постепенно заполняется таблица на доске:

II признак

III признак

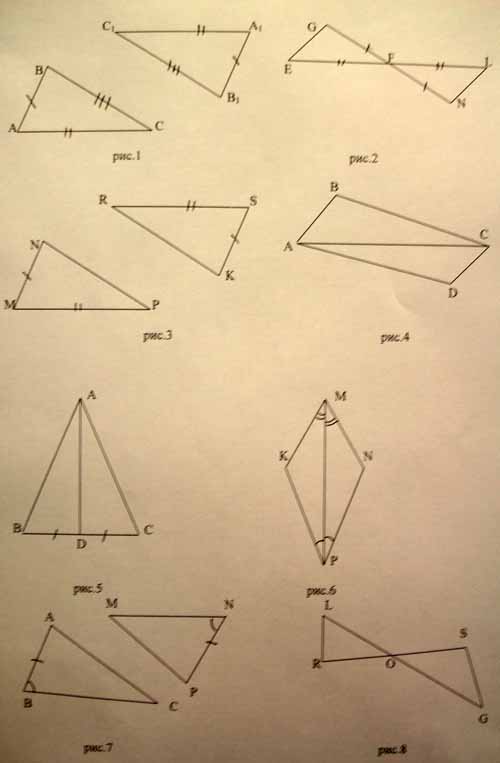
4. Проверяются работы учащихся, выполнявших задания по карточкам. Они задают друг другу по теоретическому вопросу.

Решение (карточка №2).

1) САО = DBO по двум сторонам и углу между ними (АО=BO, СО=DO, АОС= BOD - вертикальные углы);

2) РСАО = СА + СО + АО;

3) CА =ВD = 4см, АО = ВО = 3см;

4) РСАО = 4 + 5 + 3 = 12(см).

Ответ: 12см.

III. Выполнение заданий учебника.

Учитель:

- А теперь, ребята, мы поработаем все вместе, в тетрадях.

№160(а). Прямая а проходит через середину отрезка AB и перпендикулярна к нему. Докажите, что каждая точка прямой а равноудалена от точек A и B.

Учитель:

- Выполните рисунок к данной задаче. (Пройти по рядам, посмотреть, помочь).

- Чтобы у всех было единое обозначение, точку на прямой обозначим буквой К.

- Как вы понимаете: точка равноудалена от точек А и В?

- А теперь проверим, правильно ли вы выполнили рисунок. (Раскрыть доску с рисунком)

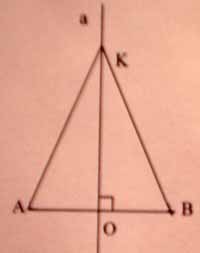
Доказательство:

АОК = BОК по двум сторонам и углу между ними (АО=ВО, т.к. О - середина AB, АОК =ВОК, т.к. а АВ, ОК - общая сторона), тогда АК=ВК.

Учитель:

- Так что мы с вами доказали?

- Т.о. мы доказали, что любая точка равноудалена от точек A и B.

IV. Физминутка.

V. Тестирование. (Дифференцированные задания)



Учитель:

- Я вам предлагаю тест трёх уровней. Ответы на вопросы теста вы должны внести в карту ответов. Обратите внимание: карт ответов у вас два, т.е. вам необходимо продублировать ответы. Один вы сдадите мне, а другой оставите себе для самопроверки. Время выполнения теста 5 минут.

Карта ответов.

УРОВЕНЬ __I_____ Вариант______

Фамилия, имя___________________

Класс 7 А

1

2

3

Баллы

1

2

2

Вариант

ответа

Оценка

(У II-III уровней за первое задание два балла)

I уровень.

Вариант 2.

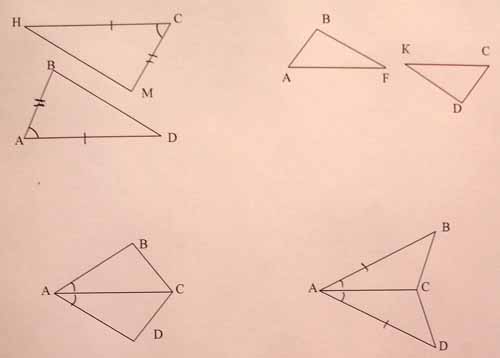
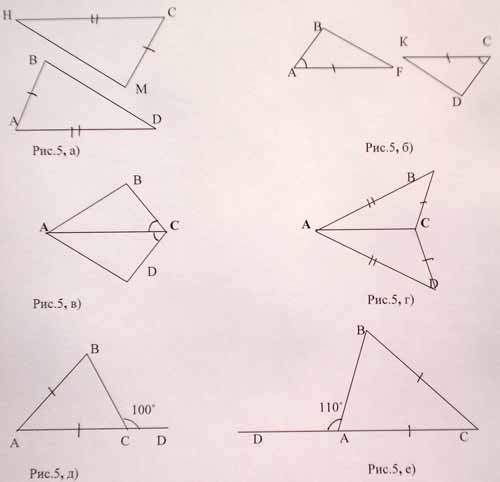
1. В треугольниках ABD и СМН (рис.5,а)

AB = СМ, AD =CН.

ABD = CМН, если …

а) В = М; б) А = Н; в)А = С

2. АС - биссектриса BAD (рис.5,в).

ВСА = =DCA. АВС =ADC

по …

а) двум сторонам и углу между ними;

б) стороне и прилежащим к ней углам;

в) трём сторонам.

3. BCD =100˚ (рис.5, д). Найдите ABC.

Ответы: а) 40˚; б) 80˚; в) 100˚.

1. В треугольниках ABF и CDK (рис.5,б)

A = C, AF= CК.

ABF = CDK, если …

а) В = D; б) F = К; в) F = D.

2. DC = BC, AB = AD (рис. 5,г)

ВAС =DAC по…

а) двум сторонам и углу между ними;

б) стороне и прилежащим к ней углам;

в) трём сторонам.

3. BAD =110˚ (рис.5,е). Найдите ABC.

Ответы: а) 110˚; б) 35˚; в) 70˚.

II уровень.

Вариант 2.

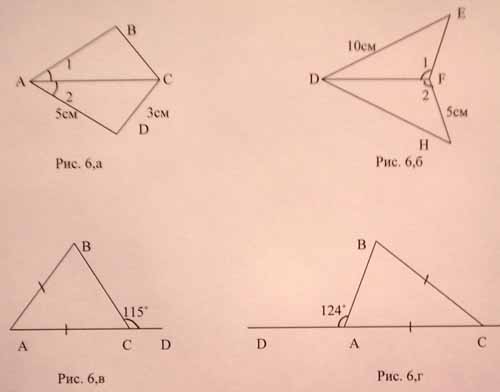
1. В треугольниках АВС и ADC (рис. 6, а)

1 = 2, AD = 5cм, DC = 3см.

Найдите AB.

Ответы: а) 5см; б) 3см; в) недостаточно данных.

2. Периметр равнобедренного треугольника равнобедренного треугольника равен 28см, а его боковая сторона равна 9см.

Найдите длину основания треугольника.

Ответы: а) 10см; б) 14,5см; в) 29см.

3. BCD =115˚ (рис.6, в). Найдите ABC.

Ответы: а) 50˚; б) 65˚; в) 75˚.

1. В треугольниках DEF и DHF (рис. 6, б)

1 = 2, FE = FH, FH = 5cм, DE=10cм

Найдите DH.

Ответы: а) 6см; б) 10см; в) недостаточно данных.

2. Основание равно 12см, а его периметр равен 38см.

Найдите боковые стороны треугольника.

Ответы: а) 12см, 12см; б) 11см, 15см;

в) 13см, 13см.

3. BAD =124˚ (рис.6, г). Найдите ACB.

Ответы: а) 56˚; б) 68˚; в) 28˚.

III уровень.

Вариант 2.

1. В треугольниках АВС и А1В1С1

А = А1, AВ = А1В1, АС = А1С1.

На сторонах BC и В1С1 отмечены точки К и К1, такие, что СК = С1К1. АВ = 10cм, ВС = 13см, С1К1= 6см.

Найти В1К1.

Ответы: а) 10см; б) 7см; в) 19см.

2. Периметр треугольника ABC равен 39см. Одна из сторон на 4см больше второй и на 2см больше третьей стороны. Найдите стороны ABC.

Ответы: а) 9см, 13см, 17см;

б) 11см, 13см, 15см;

в) 10см, 12см, 17см.

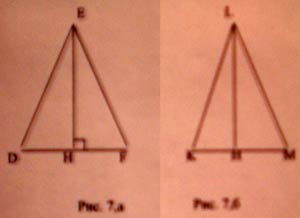
3. В равнобедренном треугольнике DEF основание DF = 12cм, EH - высота (рис. 7, а).

Найдите DH.

Ответы: а) 6см; б) 12см; в) 24см.

1. В треугольниках АВС и А1В1С1

В = В1, АВ = А1В1, ВС = В1С1. На сторонах АC и А1С1 отмечены точки D и D1 так, что АD = А1D1. АВ = 12см, АС = 9см, D1С1 = 3см. Найти А1D1.

Ответы: а) 12см; б) 9см; в) 6см.

2. Найдите стороны треугольника MNP, если его периметр равен 63см, одна из сторон на 3см меньше второй и в 2 раза меньше третьей.

Ответы: а) 15см, 18см, 30см;

б) 12,2см, 24,4см, 26,4см;

в) 14см, 17см, 28см.

3. В равнобедренном треугольнике KLM c основанием КМ боковая сторона равна 9см, а периметр - 28см. LН - биссектриса треугольника (рис7,б). Найдите НM.

Ответы: а) 14см; б) 5см; в) 9см .

Учитель:

- Время, отведённое на тесты, закончилось. Передайте, пожалуйста, свои карты ответов. Не забудьте продублировать результаты теста. А сейчас проверьте свои работы по предложенной таблице. Подсчитайте сумму баллов. Поднимите руку, кто оценил свою работу на «5», кто - на «4», кто - на «3».

• 6 баллов - «5»;

• 5 баллов - «4»;

• 3 балла - «3»;

• 0-2балла - «2».

Ответы на тесты:

I уровень

вариант 1

I уровень

вариант 2

II уровень

вариант 1

II уровень

вариант 2

III уровень

вариант 1

III уровень

вариант 2

1

в

б

в

б

б

в

2

б

в

а

в

б

а

3

б

в

б

б

а

б

VI. Практическое применение знаний.

Учитель:

- После следующей задачи вы должны ответить на вопрос: « Где на практике применяются признаки равенства треугольников?».

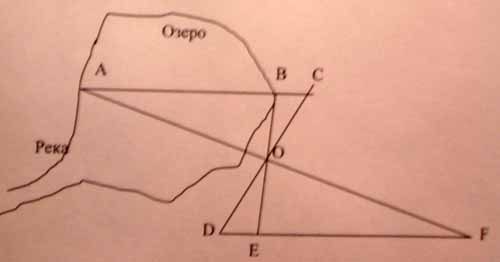
- Представьте, что вы на берегу озера и вам нужно определить ширину озера с помощью знаний, полученных на уроках геометрии. В точках B,C,O, D,E и F стоят колышки, а в точке A - дерево. Нам необходимо найти длину расстояния AB, а расстояния EF мы можем измерить с помощью рулетки. Как, зная эти расстояния, найти расстояние AB, если OC=OD, OB=OE?

Решение:

- Чтобы найти расстояние AB надо доказать:

1. СОВ = DOE;

2. AОC = FOD.

1) СОВ = DOE по двум сторонам и углу между ними (ОС = OD, OB= OE, COB = DOE - вертикальные углы).

2) AOC = FOD по стороне идвум прилежащим к ней углам (ОС = OD, ACO = FDО из равенства треугольников СОВ и DОЕ, СOA = DOF- вертикальные углы).

3) АВ = АС - ВС, F E = DF - DE, но АС = FD, т.к. AОC = FOD, BC = ED , т.к. СОВ = DОЕ, тогда АВ = EF.

Где на практике применяются признаки равенства треугольников?

VI. Подведение итогов урока.

Цель: развивать способность учащихся к анализу и к критическому отношению при решении задач, способность к содержательному обобщению и рефлексии.

Работа проходит в форме беседы.

- Ребята, чем мы сегодня занимались на уроке?

- Какие знания по теме «Треугольники» вы сегодня применяли при решении задач?

- Почему так важно знать признаки равенства треугольников? (С помощью признаков равенства треугольников решаются также алгебраические, географические, физические задачи.)