- Учителю
- Рабочая программа по алгебре 10 класс Мордкович
Рабочая программа по алгебре 10 класс Мордкович

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
1.1. Нормативная база
Рабочая программа по алгебре и началам анализа на 2015-2016 учебный год ориентирована на учащихся 10 класса, разработана на основе следующих нормативных правовых документов и инструктивно-методических материалов:
-
Федеральный Закон от 29.12.2012 № 273- ФЗ «Об образовании в Российской Федерации»;
-
Приказ Минобразования России от 5 марта 2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»;
-
Приказ Минобразования России от 9 марта 2004 №1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования» (в ред. приказов Минобрнауки РФ от 20.08.2008 № 241, от 30.08.2010 № 889, от 03.06.2011 № 1994, от 01.02.2012 № 74);
-
Постановление Главного Государственного санитарного врача Российской Федерации «Об утверждении СанПин 2.4.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» от 29.12.2010 №189;
-
Приказ Минобрнауки России от 31.03.2014 № 253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;
-
Приказ Министерства образования Оренбургской области № 01 - 21 /1063 от 13.08.2014 года «Об утверждении регионального базисного учебного плана и примерных учебных планов для общеобразовательных учреждений Оренбургской области»;
-
Устав МАОУ «Андреевская СОШ»;
-
Учебный план МАОУ «Андреевская СОШ» на 2015-2016 учебный год (Протокол № 1 от 27.08.2015г.).
-
Авторская программа Алгебра и начала анализа 10-11 классы. авт.-сост. И. И. Зубарева, А.Г. Мордкович. - М.: Мнемозина, 2007.
1.2 Цель
Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
1.3 Задачи:
-
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
-
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
-
знакомство с основными идеями и методами математического анализа.
2. ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа».
Содержание образования развивается в следующих направлениях:
- систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
- развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
- систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
- расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
- развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
- совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
- формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
3. ОПИСАНИЕ МЕСТА УЧЕБНОГО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
Учебным планом предусмотрено: количество уроков в год 102 ч., 3 часа в неделю.
I четверть - 27 ч.
II четверть - 21ч.
III четверть - 30ч.
IV четверть - 24ч.
4. ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ ПРОГРАММЫ
В результате изучения математики на базовом уровне ученик должен:
знать/понимать:
-
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
-
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
-
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
-
вероятностный характер различных процессов окружающего мира;
Алгебра
уметь
-
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах:
-
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
-
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
-
определять значение функции по значению аргумента при различных способах задания функции;
-
строить графики изученных функций;
-
описывать по графику и в простейших случаях по формуле1 поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
-
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
уметь
-
вычислять производные и первообразные элементарных функций, используя справочные материалы;
-
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
-
вычислять в простейших случаях площади с использованием первообразной;
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
-
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
-
составлять уравнения и неравенства по условию задачи;
-
использовать для приближенного решения уравнений и неравенств графический метод;
-
изображать на координатной плоскости множества решений простейших уравнений и их систем;
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
построения и исследования простейших математических моделей;
Элементы комбинаторики, статистики и теории вероятностей
уметь
-
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
-
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
-
анализа информации статистического характера.
5. СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
Числовые функции (9ч)
Определение и способы задания числовой функции. Область определения и область значений функции. Свойства функций. Исследование функций. Чтение графика. Определение и задание обратной функции. Построение графиков прямой и обратной функции.
Тригонометрические функции (26ч)
Числовая окружность. Длина дуги числовой окружности. Числовая окружность на координатной плоскости. Определение синуса и косинуса на единичной окружности. Определение тангенса и котангенса. Тригонометрические функции числового аргумента. Упрощение тригонометрических выражений. Тригонометрические функции углового аргумента. Решение прямоугольных треугольников. Формулы приведения. Функция y=sin x, её свойства и график. Функция y=cos x, её свойства и график. Периодичность функций y=sin x, y=cos x. Построение графика функций y=mf(x) и y=f(kx) по известному графику функции y=f(x). Функции y=tg x и y=ctg x, их свойства и графики.
Тригонометрические уравнения (10ч)
Первые представления о решении тригонометрических уравнений. Определение и вычисление арккосинуса. Решение уравнения cos t=a. Определение и вычисление арксинуса. Решение уравнения sin t=a. Арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a. Простейшие тригонометрические уравнения. Различные методы решения уравнений. Однородные тригонометрические уравнения.
Преобразование тригонометрических выражений (15ч)
Синус и косинус суммы и разности аргументов. Тангенс суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.
Производная (31ч)
Определение числовой последовательности и способы её задания. Свойства числовых последовательностей.
Предел последовательности. Свойства сходящихся последовательностей. Сумма бесконечной геометрической прогрессии. Вычисление пределов.
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Дифференцирование функции y=f(kx+m). Формулы для вычисления производных. Производная сложной функции. Применение производной для исследования функций на монотонность и экстремумы.
График функции, график производной. Построение графиков функций.
Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции y=f(x).
Задачи с параметром. Графическое решение.
Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке.
Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. Текстовые и геометрические задачи на отыскание наибольших и наименьших значений величин.
Обобщающее повторение (11 часов)
Итого 102 часа
6. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
-
Раздел
Количество часов
1
Числовые функции
9 часов
2
Тригонометрические функции
26 часов
3
Тригонометрические уравнения
10 часов
4
Преобразование тригонометрических выражений
15 часов
5
Производная
31 час
6
Обобщающее повторение
11 часов
Календарно-тематическое планирование по алгебре и началам анализа для 10 класса
Всего: 102 часа (3 часа в неделю)Числовая функция. Область определения функции. Независимая и зависимая переменные. Область значений функции. График функции. Кусочно-заданная функция.
Способы задания числовой функции: словесный, табличный, аналитический, функционально-графический
1.09
Нахождение области определения функции
1
3.09
Построение графиков функций
1
4.09
Свойства функции. Монотонность. Ограниченность.
1
Возрастающая на множестве функция. Убывающая на множестве функция. Ограниченная снизу на множестве функция. Ограниченная сверху на множестве функция. Исследование функции на монотонность и ограниченность.
7.09
Свойства функций. Четность
1
Четная и нечетная функции. Исследование функции на четность. Симметричное множество
8.09
Входная контрольная работа. ГБУ «Региональный центр развития образования»
1
10.09
Свойства функций. Нахождение наибольшего и наименьшего значений функции
1
Наименьшее и наибольшее значения функции. Свойство выпуклости функции. Свойство непрерывности функции.
14.09
Диагностическая работа № 1
в рамках мониторинга
1
15.09
Обратная функция
1
Обратимая функция. Обратная функция. Монотонность функции - достаточное условие ее обратимости. Точки симметрии относительно прямой у=х.
17.09
Построение графиков обратных функций
1
21.09
Построение графиков обратных функций
1
22.09
Числовая окружность
1
Числовая окружность. Четверти числовой окружности. Положительное и отрицательное направления обхода числовой окружности. Нахождение на числовой окружности точек, соответствующих данному числу. Запись чисел, соответствующих заданной точке числовой окружности
24.09
Числовая окружность
Решение задач
1
28.09
Числовая окружность на координатной плоскости
1
Координатная плоскость. Числовая окружность на координатной плоскости. Координаты точки окружности
29.09
Числовая окружность на координатной плоскости. Решение задач
1
Числовая окружность.
Обучение решению задач
1.10
Решение простейших неравенств
1
5.10
Контрольная работа №1 по теме «Свойства функции. Числовая окружность»
1
6.10
Синус и косинус
1
Синус и косинус числа. Свойства синуса и косинуса. Знаки синуса и косинуса по четвертям окружности.
8.10
Тангенс и котангенс
1
12.10
Синус и косинус
Тангенс и котангенс
1
Тангенс и котангенс числа. Свойства тангенса и котангенса. Знаки тангенса и котангенса по четвертям окружности
13.10
Тригонометрические функции числового аргумента
1
Тригонометрические функции числового аргумента. Соотношения, связывающие значения различных тригонометрических функций
15.10
Тригонометрические функции числового аргумента
1
19.10
Тригонометрические функции углового аргумента
1
Тригонометрические функции углового аргумента. Синус, косинус, тангенс и котангенс угла. Градусная мера угла. Радианная мера угла. Формулы для вычисления значений синуса, косинуса, тангенса и котангенса угла
20.10
Тригонометрические функции углового аргумента
1
22.10
Формулы приведения
1
Формулы приведения. Мнемоническое правило. Правила перехода функций
26.10
Формулы приведения
1
27.10
Контрольная работа №2 по теме «Тригонометрические функции числового и углового аргумента.»
1
29.10
Функция у = sinх, ее свойства и график
1
Тригонометрическая функция у = sinх. Свойства и график функции. Синусоида. Полуволна синусоиды. Арка синусоиды
9.11
Функция у = sinх, ее свойства и график
1
10.11
Функция у =сosх, ее свойства и график
1
Тригонометрическая функция у = сosх. Свойства и график функции. Косинусоида. Полуволна косинусоиды. Арка
косинусоиды
12.11
Функция у =сosх, ее свойства и график
1
16.11
Периодичность функций
y=sinх, у=сosх
1
Периодическая функция. Период функции. Основной период функции
17.11
Преобразования графиков тригонометрических функций. Построение графика функции у =mf(х) по известному графику функции у =f(х)
1
Растяжение от оси абсцисс с коэффициентом. Сжатие к оси абсцисс с коэффициентом. Построение графика функции у =mf(х) по известному графику функции у =f(х). Преобразование симметрии относительно оси абсцисс
19.11
Преобразования графиков тригонометрических функций.
Построение графика функции у =f(кх) по известному графику функции y=f(x)
1
Сжатие к оси ординат с коэффициентом. Построение графика функции у =f(кх) по известному графику функции у =f(х). Преобразование симметрии относительно оси ординат
23.11
Функции у =tgх,
у = ctgх их свойства и графики
1
Тригонометрические функции у =tgх и у = ctgх. Свойства и графики функций. Тангенсоида. Главная ветвь тангенсоиды
24.11
Функции у =tgх,
у = ctgх их свойства и графики
1
26.11
Контрольная работа №3 по теме «Графики и свойства тригонометрических функций».
1
30.11
Арккосинус.
Решение уравнения сos t =а
1
Арккосинус числа. Уравнение сost =а. Формула корней уравнения сos t =а.
Решение неравенств вида сost >а, Сos t < а
1.12
Решение уравнений вида
Сos t =а
1
3.12
Арксинус. Решение уравнений sin t= а
1
Арксинус числа. Уравнение sin t= а.
Формула корней уравнения sin t= а.
Решение неравенств вида sin t> а, sint< а
7.12
Решение уравнений вида
Sin t= а
1
8.12
Арктангенс и арккотангенс. Решение уравнений tgt = a, ctgt = a
1
Арктангенс и арккотангенс числа. Уравнения tgt = a и
ctgt = a. Формула корней уравнений tgt = a и ctgt = a. Решение неравенств вида tgt> a, tgt< a, ctgt> a, ctgt< a.
10.12
Тригонометрические уравнения простейшие
1
Простейшие тригонометрические уравнения. Формулы простейших тригонометрических уравнений
14.12
Методы решения тригонометрических уравнений
1
Два основных метода решения тригонометрических уравнений: введение новой переменной и разложение на множители
15.12
Диагностическая работа № 2
в рамках мониторинга
1
17.12
Однородные тригонометрические уравнения
1
Однородные тригонометрические уравнения первой и второй степени. Алгоритм решения однородных уравнений второй степени
21.12
Решение тригонометрических уравнений
1
Проверка знаний и умений учащихся по теме «Тригонометрические уравнения»
22.12
Контрольная работа № 4 по теме «Тригонометрические уравнения»
1
24.12
Синус и косинус суммы и разности аргументов
1
Формулы синуса и косинуса суммы и разности аргументов
Формулы синуса и косинуса суммы и разности аргументов
28.12
Преобразования тригонометрических выражений с применением формул
1
29.12
Решение уравнений с применением формул
1
Формулы синуса и косинуса суммы и разности аргументов
11.01
Решение неравенств с применением формул
1
12.01
Тангенс суммы и разности аргументов
1
Формулы тангенса суммы и разности аргументов
14.01
Преобразования тригонометрических выражений с применением формул
1
Формулы котангенса суммы и разности аргументов
18.01
Формулы двойного аргумента
1
Формулы двойного аргумента (угла), кратного угла, половинного аргумента
19.01
Формулы понижения степени
1
Формулы понижения степени тригонометрических выражений
21.01
Решение уравнений с применением формул
1
Формулы двойного аргумента (угла), кратного угла, половинного аргумента, формулы двойного аргумента
25.01
Преобразование сумм тригонометрических функций в произведения
1
Формулы преобразования сумм тригонометрических функций в произведения
26.01
Решение уравнений с применением формул
1
28.01
Преобразование выражений Аsinx+ Вcosх в выражения вида Сsin (x+t)
1
Преобразование выражений
Аsinx+ Вcosх к вида Сsin (x+t)
Вспомогательный (дополнительный) аргумент
1.02
Контрольная работа №5 по теме «Преобразованиие тригонометрических выражений».
1
2.02
Преобразование произведений тригонометрических функций в суммы
1
Формулы преобразования произведений тригонометрических функций в суммы
4.02
Преобразование произведений тригонометрических функций в суммы
Основные формулы тригонометрии
1
Формулы, связывающие тригонометрические функции одного и того же аргумента. Формулы, связывающие функции аргументов, из которых один вдвое больше другого. Формулы сложения аргументов. Преобразование сумм тригонометрических функций в произведения. Преобразование произведений тригонометрических функций в суммы. Формулы приведения
8.02
Числовые последовательности и их свойства
1
Ограниченная сверху последовательность. Ограниченная снизу последовательность. Возрастающая и убывающая последовательности. Предел последовательности. Формула предела последовательности. Окрестность точки. Радиус окрестности. Точки сгущения. Сходящиеся и расходящиеся последовательности. Свойства сходящихся последовательностей. Теорема Вейерштрасса
9.02
Предел последовательности
1
11.02
Сумма бесконечной геометрической прогрессии
1
Сумма бесконечной геометрической прогрессии. Составление математической модели
15.02
Перевод периодической дроби в обыкновенную
1
Сумма бесконечной геометрической прогрессии. Составление математической модели
16.02
Предел функции на бесконечности
1
Предел функции. Утверждения для вычисления предела функции на бесконечности
18.02
Предел функции в точке
1
Предел функции в точке. Непрерывная функция в точке. Теорема об арифметических операциях над пределами
22.02
Приращение аргумента. Приращение функции
1
Приращение аргумента. Приращение функции. Формула для вычисления приращения функции. Определение непрерывной функции с точки зрения приращения аргумента и функции
25.02
Определение производной. Задачи, приводящие к понятию производной
1
Задача о скорости движения. Мгновенная скорость. Формула мгновенной скорости. Касательная к кривой в точке. Задача о касательной к графику функции. Формула для вычисления углового коэффициента касательной
29.02
Определение производной, ее физический и геометрический смысл
1
Производная функции в точке. Физический (механический) смысл производной. Геометрический смысл производной
1.03
Алгоритм нахождения производных
1
Алгоритм нахождения производных. Дифференцируемая функция в точке. Дифференцирование функции. Взаимосвязь между дифференцируемостью и непрерывностью функции в точке
3.03
Вычисление производных
Формулы дифференцирования
1
Формулы дифференцирования
7.03
Вычисление производных
Правила дифференцирования
1
Правила дифференцирования
10.03
Дифференцирование функции
у =f(кх +m)
1
Правила дифференцирования. Производные суммы, произведения, частного функций. Метод математической индукции
14.03
Контрольная работа №6 по теме «Определение производной. Привила дифференцирования».
1
15.03
Уравнение касательной к графику функции
1
Уравнение касательной к графику функции. Угловой коэффициент. Алгоритм составления уравнения касательной к графику функции
17.03
Составление уравнения касательной к графику функции
1
31.03
Применение производной для исследования функций
Исследование функций на монотонность
1
Применение производной для исследования функций на монотонность и знакопостоянство. Возрастающие и убывающие дифференцируемые функции. Постоянная функция. Теоремы о взаимосвязи знака производной и характера монотонности функции на промежутке
4.04
Точки экстремума и их нахождение
1
Точка минимума и точка максимума функции. Точки экстремума. Стационарные и критические точки. Необходимые и достаточные условия экстремума. Полюсы функции. Алгоритм исследования функции на монотонность и экстремумы
5.04
Применение производной для исследования функций
1
7.04
Построение графиков функций
Алгоритм построения графиков
1
Применение свойств функций для построения их графиков. Горизонтальная и вертикальная асимптоты графика функции
11.04
Построение графиков функций
1
Применение свойств функций для построения их графиков. Горизонтальная и вертикальная асимптоты графика функции
12.04
Построение графиков функций
1
14.04
Контрольная работа №7 по теме «Применение производной для исследования функций».
1
18.04
Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке
1
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке.
19.04
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на незамкнутом промежутке. Теорема о критических точках функции, непрерывной на незамкнутом промежутке
21.04
Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке
1
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на отрезке. Теорема о критических точках функции, непрерывной на незамкнутом промежутке
25.04
Задачи на нахождение наибольших и наименьших значений величин
1
Задачи на нахождение наибольших и наименьших значений величин (задачи на оптимизацию), схема их решения. Оптимизируемая величина (О. В.). Независимая переменная (Н. П.). Реальные границы изменения Н. П. Составление математической модели
26.04
Задачи на нахождение наибольших и наименьших значений величин
1
Задачи на нахождение наибольших и наименьших значений величин (задачи на оптимизацию), схема их решения. Оптимизируемая величина (О. В.). Независимая переменная (Н. П.). Реальные границы изменения Н. П. Составление математической модели
28.04
Задачи на нахождение наибольших и наименьших значений величин
1
2.05
93-94
Контрольная работа №8 по теме «Применение производной для отыскания наибольшего и наименьшего значений».
2
3.05
95.
Повторение
Тригонометрические функции
1
Числовая окружность. Синус, косинус, тангенс, котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Формулы приведения. Тригонометрические функции y=sinx, y=cosx, y=tgx, y=ctgx.
Свойства и графики функций
5.05
96.
Повторение
Тригонометрические уравнения
1
Арккосинус, арксинус, арктангенс, арккотангенс. Простейшие тригонометрические уравнения вида cost=a, sint=a, tgt=a, ctgt=a. Формулы корней уравнений. Решение неравенств вида cost>a, costa, sinta, tgta, ctgt
10.05
97.
Повторение
Тригонометрические уравнения
1
12.05
98.
Повторение
Тригонометрические выражения
1
Формулы двойного аргумента (угла), кратного угла, половинного аргумента. Формулы понижения степени тригонометрических выражений. Формулы сложения аргументов. Преобразование сумм тригонометрических функций в произведения. Преобразование произведений тригонометрических функций в суммы. Формулы приведения
16.05
98.
Контрольная работа за год
в рамках мониторинга
1
17.05
99.
Повторение
Производная
1
Производная функции. Физический и геометрический смысл производной. Алгоритм нахождения производных. Формулы дифференцирования. Правила дифференцирования. Уравнение касательной к графику функции. Применение производной для исследования функций. Построение графиков функций
19.05
100
Повторение
Применение производной
1
23.05
101
Повторение
Построение графиков функций и использование их свойств
1
Определение значение функции по значению аргумента при различных способах задания функции
24.05
102
Повторение и обобщение изученного в 10 классе
1
26.05
Изменения внесенные в программу:
4 часа обобщающего повторения выделено на написание контрольных и диагностических работ в рамках мониторинга
7. УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
Список рекомендованной литературы для учителя:
1. Учебник автор Г.М. Мордкович
2. Журнал «Математика в школе»
3. Блиц-опрос «Математика -10» автор Е.Е. Тульчинская.
4. «Преподавание математики в 10 классе» под редакцией В.И. Жохова
5. «Математические диктанты для 10 класса» составитель В.И. Жохов
6. «Сборник задач и примеров для 10 класса»
7. «Попробуй реши» - сборник задач В. Щурковой.
8. Л.С. Атанасян и др. Геометрия, 10-11. Учебник. М.: Просвещение, 2011
Список рекомендованной литературы для учеников:
-
Учебник 10 классас автор Г.М. Мордкович
-
Блиц-опрос 10 класс автор Е.Е. Тульчинская
-
«Попробуй реши» - сборник задач В. Щурковой.
«Сборник задач и примеров для 10-11 класса»
Печатные пособия
-
Демонстрационный материал в соответствии с основными темами программы обучения
-
Карточки с заданиями по математике
-
Портреты выдающихся деятелей математики
Учебно- практическое и учебно- лабораторное оборудование
-
Комплект чертежных инструментов: линейка, транспортир, угольник, циркуль.
Технические средства обучения:
-
Компьютер
-
Мультимедийный проектор
-
Экран
Интернет-сайты
www.ed.gov.ru - Сайт Министерства образования РФ
www.obrnadzor.gov.ru/attestat/ - Федеральная служба по надзору в сфере образования (государственная итоговая аттестация школьников)
www.prosv.ru - сайт издательства «Просвещение» (рубрика «Математика»)
http:/www.mnemozina.ru - сайт издательства Мнемозина (рубрика «Математика»)
http:/www.drofa.ru - сайт издательства Дрофа (рубрика «Математика»)
www.profile-edu.ru - Рекомендации и анализ результатов эксперимента по профильной школе. Разработки элективных курсов для профильной подготовки учащихся. Примеры учебно-методических комплектов для организации профильной подготовки учащихся в рамках вариативного компонента.
www.edu.ru - Центральный образовательный портал, содержит нормативные документы Министерства, стандарты, информацию о проведение эксперимента.
www.ed.gov.ru - На сайте представлена нормативная база: в хронологическом порядке расположены законы, указы, которые касаются как общих вопросов образования так и разных направлений модернизации.
www.ege.edu.ru сервер информационной поддержки Единого государственного экзамена.
www.internet-scool.ru - сайт Интернет - школы издательства Просвещение. Учебный план разработан на основе федерального базисного учебного плана для общеобразовательных учреждений РФ и представляет область знаний «Математика». На сайте представлены Интернет-уроки по алгебре и началам анализа и геометрии, с включают подготовку сдачи ЕГЭ.
www.intellecctntre.ru - сайт издательства «Интеллект - Центр» содержит учебно-тренировочные материалы для подготовки к ЕГЭ по математике, сборники тестовых заданий.
www.shevkin.ru - Проект Shevkin.ru. Задачи школьных математических олимпиад. Дидактический материал к УМК Никольского.
www.abitu.ru/start/about.esp (программа «Юниор - старт в науку»);
vernadsky.dnttm.ru/ (конкурс им. Вернадского);
www.step-into-the-future.ru/ (программа «Шаг в будущее)
www.mccme.ru/olympiads/mmo/ - Московский центр непрерывного математического образования. Московские математические олимпиады. Задачи окружных туров олимпиады для школьников 5-11 классов начиная с 2000 года. Задачи городских туров олимпиады для школьников 8-11 классов начиная с 1999 года. Все задачи с подробными решениями и ответами. Новости олимпиады. Победители и призеры олимпиад. Статистика.
olympiads.mccme.ru/regata/ - математические регаты.
olympiads.mccme.ru/matboi/ - Математический турнир математических боев.
olympiads.mccme.ru/turlom - Турнир имени М.В.Ломоносова.
kyat.mccme.ru/ - Научно-популярный физико-математический журнал «Квант».
abitu.ru/distance/zftshl.html - Заочная физико-математическая школа при МФТИ.
attend.to/dooi - Дистанционные олимпиады.
aimakarov.chat.ru/school/school.html - Школьные и районные математические олимпиады в Новосибирске. Задачи для 3-11 классов с 1998 года по настоящее время.
Без решений. Раздел занимательных и веселых задач.
zaba.ru/ - Олимпиадные задачи по математике: база данных. Около 8000 задач школьных, региональных, всероссийских и международных конкурсов, олимпиад и турниров по математике. Многие задачи с ответами, указаниями, решениями. До 2001 года (включительно). Возможности поиска.
homepages.compuserve.de/chasluebeck/matemat/task1.htm - Задачи некоторых математических олимпиад и турниров. Задания региональных (Москва, Урал, Луганск, Волгоград и др.) и других (МФТИ, Соросовская и т.д.) олимпиад по математике
ПРИЛОЖЕНИЕ
ОЦЕНОЧНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
Входная контрольная работа 10 класс
На выполнение контрольной работы дается 90 мин. В каждом задании сначала запишите номер выполняемого задания, а затем полное решение и ответ. Учебники, справочные материалы, калькуляторы использовать запрещается.
Желаем удачи!
Вариант 1
-
В классе 16 девочек, что составляет 40%. Сколько в классе мальчиков?
-
Упростите выражение
 .
.
-
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
-
А
Б
В
-
Решите неравенство
 .
.
-
Один из смежных углов в 8 раз больше другого. Найдите наименьший угол.
-
Найдите область определения функции
 .
.
-
Найдите площадь параллелограмма, у которого стороны 12 см. и 5 см., один из углов
 .
.
-
В арифметической прогрессии а1 = - 2, а5 = 30. Найдите d.
-
Вычислите
 .
.
-
Решите систему уравнений

-
Первая труба пропускает на 2 литра воды в минуту меньше чем вторая. Сколько литров воды в минуту пропускает первая труба, если бак объемом 120 литров она заполняет на 2 минуты дольше, чем вторая.
-
Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.
Вариант 2
-
В группе 28 мальчиков, что составляет 70% детей. Сколько в группе девочек?
-
Упростите выражение
 .
.
-
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
ФОРМУЛЫ
-
А
Б
В
-
Решите неравенство
 8х -
2.
8х -
2.
-
Один из смежных углов на 24 градусов больше другого. Найдите наименьший угол.
-
Найдите область определения функции
 .
.
-
Найдите площадь параллелограмма, у которого стороны 13 см. и 6 см., один из углов
 .
.
-
В арифметической прогрессии а7 = 29, d = - 3,5. Найдите а1.
-
Вычислить
 .
.
-
Решите систему уравнений

-
Первая труба пропускает на 4 литра воды в минуту меньше чем вторая. Сколько литров воды в минуту пропускает первая труба, если бак объемом 140 литров она заполняет на 4 минуты дольше, чем вторая.
-
Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 3. Найдите высоту ромба.
________________________________________________________________________________________________________________________
Контрольная работа №1
Определение числовой функции. Числовая окружность
Вариант 1
1. Найдите область определения функции:  .
.
2. Найдите область значений функции: ![]() .
.
3. Найдите на числовой окружности точку:
![]()
4. Найдите наименьшее положительное и наибольшее
отрицательное числа, которым на числовой окружности
соответствует точка с координатами: 
5. Найдите на числовой окружности тачки с абсциссой или ординатой, удовлетворяющей заданному неравенству, и запишите (с помощью двойного неравенства), каким числам t они соответствуют:

Контрольная работа №1
Определение числовой функции. Числовая окружность
Вариант 2
1. Найдите область определения функции:  .
.
2. Найдите область значений функции: ![]() .
.
3. Найдите на числовой окружности точку:
![]()
4. Найдите наименьшее положительное и наибольшее
отрицательное числа, которым на числовой окружности
соответствует точка с координатами: 
5. Найдите на числовой окружности тачки с абсциссой или ординатой, удовлетворяющей заданному неравенству, и запишите (с помощью двойного неравенства), каким числам t они соответствуют:

________________________________________________________________________________________________________
Контрольная работа №2
Определение тригонометрических функций
Вариант 1
1. Найдите значение выражения:

2. Решите уравнение: ![]() .
.
3. Найдите наименьшее и наибольшее значение выражения:
![]() .
.
4. Укажите все значения t, при которых выражение
![]() не имеет
смысла.
не имеет
смысла.
5. Определите знак выражения: ![]() .
.
6. Решите неравенство: ![]() .
.
Контрольная работа №2
Определение тригонометрических функций
Вариант 2
1. Найдите значение выражения:

2. Решите уравнение:  .
.
3. Найдите наименьшее и наибольшее значение выражения:
![]() .
.
4. Укажите все значения t, при которых выражение
![]() не имеет
смысла.
не имеет
смысла.
5. Определите знак выражения: ![]() .
.
6. Решите неравенство: ![]() .
.
________________________________________________________________________________________________________
Контрольная работа №3
Свойства и графики тригонометрических функций
Вариант 1
1. Постройте график функции:  .
.
2. Найдите множество значений функции ![]() .
.
3. Выяснить, является ли данная функция четной или
нечетной: ![]()
4. Докажите, что функция ![]() является
периодической с периодом
является
периодической с периодом ![]() .
.
5. Сравните числа: ![]() .
.
6. Найдите наибольшее и наименьшее значение функции
![]() на
отрезке
на
отрезке ![]() .
.
7. Построить график функции у = |sin x| +1
Контрольная работа №3
Свойства и графики тригонометрических функций
Вариант 2
1. Постройте график функции:  .
.
2. Найдите множество значений функции ![]() .
.
3. Выясните, является ли данная функция четной или
нечетной: ![]() .
.
4. Докажите, что функция у = tg 3x является
периодической с периодом ![]() .
.
5. Сравните числа: ![]()
6. Найдите наибольшее и наименьшее значение функции
![]() на
отрезке
на
отрезке ![]() .
.
7. Постройте график функции ![]() .
.
_______________________________________________________________________________________________________
Контрольная работа №4
Тригонометрические уравнения
Вариант 1
1. Решите уравнения:
 .
.
2. Решите уравнения:
 .
.
3. Решите уравнение ![]() .
.
4. Решите уравнение: ![]() .
.
5. Найдите корни уравнения ![]() на
промежутке
на
промежутке ![]() .
.
Контрольная работа №4
Тригонометрические уравнения
Вариант 2
1. Решите уравнения:
 .
.
2. Решите уравнения:
![]() .
.
3. Решите уравнение ![]() .
.
4. Решите уравнение: ![]() .
.
5. Найдите корни уравнения ![]() на
промежутке
на
промежутке ![]() .
.
________________________________________________________________________________________________________
Контрольная работа №5
Преобразование тригонометрических выражений
Вариант 1
1. Решите уравнения:
 .
.
2. Докажите тождество:  .
.
3. Преобразуйте произведение в сумму ![]()
4. Найдите наименьшее и наибольшее значения функции
![]() .
.
5. Решите уравнение ![]() .
.
6. Найдите значение выражения  если
если
![]() .
.
Контрольная работа №5
Преобразование тригонометрических выражений
Вариант 2
1. Упростите выражение:
 .
.
2. Докажите тождество: ![]() .
.
3. Преобразуйте произведение в сумму ![]()
4. Найдите наименьшее и наибольшее значения функции
![]() .
.
5. Решите уравнение ![]() .
.
6. Найдите значение выражения ![]() если
известно, что
если
известно, что ![]() .
.
________________________________________________________________________________________________________
Контрольная работа №6
Определение производной и ее вычисление
Вариант 1
1. Найдите производную функции:
![]() .
.
2. Найдите производную функции:  .
.
3. Найдите значение производной функции  .
.
4. Найдите значения х, при которых значения производной
функции  отрицательны.
отрицательны.
5. Решите уравнение ![]() , если
, если
![]() .
.
6. Задайте формулой хотя бы одну функцию ![]() ,
если
,
если ![]()
Контрольная работа №6
Определение производной и ее вычисление
Вариант 2
1. Найдите производную функции:
![]() .
.
2. Найдите производную функции:  .
.
3. Найдите значение производной функции  .
.
4. Найдите значения х, при которых значения производной
функции  отрицательны.
отрицательны.
5. Решите уравнение ![]() , если
, если
![]() .
.
6. Задайте формулой хотя бы одну функцию ![]() ,
если
,
если ![]()
________________________________________________________________________________________________________
Контрольная работа №7
Построение графиков функций с помощью производной
Вариант 1
1. Найдите промежутки возрастания и убывания функции:
![]() .
.
2. Найдите критические точки функции ![]() .
Определите, какие из них являются точками максимума, а
какие - точками минимума.
.
Определите, какие из них являются точками максимума, а
какие - точками минимума.
3. Исследуйте функцию и постройте ее график:

4. Исследуйте функцию и постройте ее график: ![]()
5. Сколько корней имеет уравнение ![]() .
.
Контрольная работа №7
Построение графиков функций с помощью производной
Вариант 2
1. Найдите промежутки возрастания и убывания функции:
![]() .
.
2. Найдите критические точки функции ![]() .
Определите, какие из них являются точками максимума, а
какие - точками минимума.
.
Определите, какие из них являются точками максимума, а
какие - точками минимума.
3. Исследуйте функцию и постройте ее график:

4. Исследуйте функцию и постройте ее график: ![]()
5. Сколько корней имеет уравнение ![]() .
.
_________________________________________________________________________________________________________________________
Контрольная работа №8
Применение производной к исследованию функций
Вариант 1
1. Найдите наибольшее и наименьшее значения заданной функции на заданном отрезке:
 .
.
2. Найдите наименьшее и наибольшее значения функции
![]() на
отрезке
на
отрезке ![]() .
.
3. Докажите, что функция ![]() возрастает на всей числовой оси.
возрастает на всей числовой оси.
4. Найдите наименьшее и наибольшее значения функции
![]() на
отрезке
на
отрезке  .
.
5. Найти число, которое превышало бы свой квадрат на максимальное значение.
Контрольная работа №8
Применение производной к исследованию функций
Вариант 2
1. Найдите наибольшее и наименьшее значения заданной функции на заданном отрезке:
 .
.
2. Найдите наименьшее и наибольшее значения функции
![]() на
отрезке
на
отрезке ![]() .
.
3. Докажите, что функция ![]() убывает
на всей числовой оси.
убывает
на всей числовой оси.
4. Найдите наименьшее и наибольшее значения функции
![]() на
отрезке
на
отрезке  .
.
5. Число 18 разбить на такие два слагаемых, чтобы сумма их квадратов была наименьшей.
________________________________________________________________________________________________________
Итоговая контрольная работа 10 класс.
I вариант
Часть В.
-
Найдите значение выражения: 24
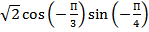 .
.
-
Решить уравнение
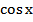 -
-  = 0
и укажите наименьший положительный корень уравнения в
градусах.
= 0
и укажите наименьший положительный корень уравнения в
градусах.
-
Найдите значение выражения:

-
Найдите
 и
и
-
Найдите значение производной функцииу = х2 - 6х + 1 в точке х0=-1.
-
Найдите значение производной функции в точке:
у = -3![]() +
2
+
2![]() ,
х0 =
,
х0 = ![]() .
.
-
Найдите точки экстремума и определите их характер:
у = х3 + 3х2 - 9х - 2.
Часть С.
-
Прямая у = 4х + 13 параллельна касательной к графику функции у = х2 - 3х + 5. Найдите абсциссу точки касания.
-
а) Решите уравнение:
2![]()
б) Укажите корни, принадлежащие
отрезку![]()
-
Найдите наибольшее и наименьшее значения функции
у = х + ![]() на
отрезке
на
отрезке ![]() .
.
Итоговая контрольная работа 10 класс.
II вариант
Часть В.
-
Найдите значение выражения: 46
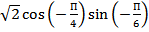 .
.
-
Решить уравнение:
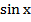 -
-
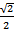 = 0
и укажите наименьший положительный корень уравнения в
градусах.
= 0
и укажите наименьший положительный корень уравнения в
градусах.
-
Найдите значение выражения:
 .
.
-
Найдите
 и
и
-
Найдите значение производной функции в точке у = х2 - 5х + 2 в точке х0=-2.
-
Найдите значение производной функции в точке:
у = 3![]() -
-![]() ,
х0 =
,
х0 = ![]() .
.
-
Найдите точки экстремума и определите их характер:
у = 2х3 - 10х2 + 6х.
Часть С.
-
Прямая у = 6х + 9 параллельна касательной к графику функции у = х2 + 7х - 6. Найдите абсциссу точки касания.
-
а) Решите уравнение:
![]()
б) Укажите корни, принадлежащие
отрезку![]()
-
Найдите наибольшее и наименьшее значения функции
у = 2х + ![]() на
отрезке
на
отрезке ![]() .
.
Итоговая контрольная работа 10 класс.
III вариант
Часть В.
-
Найдите значение выражения: 37
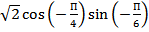
-
Решить уравнение
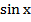 -
-
 = 0
и укажите наименьший положительный корень уравнения в
градусах.
= 0
и укажите наименьший положительный корень уравнения в
градусах.
-
Найдите значение выражения:
 .
.
-
Найдите
 и
и
-
Найдите значение производной функции у = х3 + 4х2 - 1 в точке х0=-1.
-
Найдите значение производной функции в точке:
у = ![]() -
2
-
2![]() ,
х0 =
,
х0 = ![]() .
.
-
Найдите точки экстремума и определите их характер:
у = х3 + х2 - 5х - 3.
Часть С.
-
Прямая у = -5х - 6 параллельна касательной к графику функции у = х2+ 8х - 7. Найдите абсциссу точки касания.
-
а)Решите уравнение:
![]()
б) Укажите корни, принадлежащие
отрезку![]()
-
Найдите наибольшее и наименьшее значения функции у = х +
 на
отрезке
на
отрезке 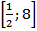 .
.
Итоговая контрольная работа 10 класс.
IV вариант
Часть В.
-
Найдите значение выражения: 34
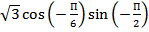 .
.
-
Решить уравнение
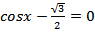 и укажите наименьший положительный корень уравнения в
градусах.
и укажите наименьший положительный корень уравнения в
градусах.
-
Найдите значение выражения:
 .
.
-
Найдите
 и
и
-
Найдите значение производной функции у = х4 - 2х - 1 в точке х0=-2.
-
Найдите значение производной функции в точке:
у = ![]() -
2
-
2![]() ,
х0=
,
х0= ![]() .
.
-
Найдите точки экстремума и определите их характер:
у = х3- х2 - х +3.
Часть С.
-
Прямая у = -3х + 8 параллельна касательной к графику функции у = х2+ 7х -6. Найдите абсциссу точки касания.
-
а) Решите уравнение:
![]()
б) Укажите корни, принадлежащие отрезку
![]()
-
Найдите наибольшее и наименьшее значения функции у = х +
 на
отрезке
на
отрезке 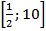 .
.
Пояснительная записка
к тексту итоговой контрольной работы
по алгебре за курс 10 класса (уч. Мордкович А.Г.).
Базовый уровень
Годовая контрольная работа составлена в соответствии с программным материалом курса «Алгебра и начала анализа» и требованиями федеральных государственных образовательных стандартов. Задания данной работы отражают следующие основные темы курса алгебры: «Тригонометрические выражения», «Тригонометрические уравнения», «Производная», «Применение производной».
Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть 1(В) состоит из 7 заданий базового уровня сложности с кратким ответом, часть 2 (С) - 3 задания повышенного уровня сложности. Структура теста аналогична структуре текстов в формате ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. Использованы задания из открытого банка задач ЕГЭ по математике. На выполнение работы отводится 45 минут.
Элементы анализа:
Часть В.
-
Нахождение значения тригонометрического выражения.
-
Решение тригонометрического уравнения и нахождение наименьшего положительного корня.
-
Нахождение значения тригонометрического выражения. Применение формулы косинуса двойного угла.
-
Нахождение значения тригонометрической функции по известной кофункции
-
Нахождение значения производной рациональной функции в точке.
-
Нахождение значения производной тригонометрической функции в точке.
-
Применение производной. Нахождение точек экстремума.
Часть С
-
Применение производной. Нахождение абсциссы точки касания.
-
а) Решение тригонометрического уравнения методом замены и сведением к квадратному
б) Нахождение корней уравнения, принадлежащих данному отрезку.
-
Применение производной. Нахождение наибольшего и наименьшего значения дробной функции на отрезке.
Всего в работе 10 заданий, т. к. № 9 (а), № 9 (б), то критерии оценивания следующие:
«3» - верно выполнено 4-7 заданий
«4» - верно выполнено 8-9 заданий
«5» - верно выполнено 10-11 заданий
СИСТЕМА ОЦЕНКИ ДОСТИЖЕНИЙ УЧАЩИХСЯ ПО МАТЕМАТИКЕ
В основе оценки знаний, умений и навыков должен лежать коммуникативный подход: осуществление учащимися любого типа школы общения и решение ими коммуникативных задач. Нормы оценки должны быть соотнесены с качеством выполнения этих задач.
Знания, умения и навыки учащихся оцениваются с учетом их индивидуальных особенностей.
1.Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
2.Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
3.Среди погрешностей выделяются ошибки и недочеты.
Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе. К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.
4.Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
1.Оценка ответа учащихся при устном и письменном опросе производится по пятибалльной системе.
2.Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им задания.
3. Итоговые отметки (за тему, четверть) выставляются по состоянию знаний на конец этапа обучения с учетом текущих отметок.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
-
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
-
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
-
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
-
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
-
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;
-
отвечал самостоятельно без наводящих вопросов учителя.
Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
-
в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.
-
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Отметка «3» ставится в следующих случаях:
-
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).
-
имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
-
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
-
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.
Отметка «2» ставится в следующих случаях:
-
не раскрыто основное содержание учебного материала;
-
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
-
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных работ учащихся.
Отметка «5» ставится в следующих случаях:
-
работа выполнена полностью.
-
в логических рассуждениях и обоснованиях нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);
Отметка «4» ставится, если:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);
-
допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
Отметка «3» ставится, если:
-
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графика, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере.
При тестировании все верные ответы берутся за 100%, тогда отметка выставляется в соответствии с таблицей:
-
Процент выполнения задания
Отметка
более 85 %
отлично
70-85%
хорошо
50-60%
удовлетворительно
менее 50%
неудовлетворительно
Система контроля складывается из следующих компонентов:
-
Математические диктанты.
-
Тесты
-
Самостоятельные работы
-
Для итогового повторения составлены итоговые зачеты.
-
Контрольные работы составлены по крупным блокам материала или главам учебника, есть итоговая контрольная работа (промежуточная аттестация)
1</</font>