Урок по геометрии для 8 класса Теорема Пифагора

Тема: теорема Пифагора.

Цель:

• познакомить учащихся с основными этапами жизни и деятельности Пифагора;

• познакомить с теоремой, показать применение теоремы к решению задач;

• показать связь геометрии с другими науками: географией, историей, литературой, биологией;

• развивать логическое мышление, вычислительные навыки, кругозор. Способность отбирать и систематизировать материал;

• воспитывать нравственную культуру.

</ Оборудование:

1.Портрет Пифагора

2.компьютер, проектор, презентация

3.Плакаты с доказательствами теоремы

4.Стенд: план урока

5.Стенд: нравственные заповеди

6.Кроссворд

7.Чертежные инструменты

8.Таблица квадратов

9.Карта мира.

Ход урока:

I. Организационный момент

• Учащиеся открывают дневники. Записывают домашнее задание.

• П.54, №483, исследовательская работа.

• Открывают тетради, записывают вопрос, чертят таблицу. Закрывают тетради, откладывают на край стола.

• Исследовательская работа.

• Задача: для закрепления мачты нужно установить четыре троса. Один конец каждого троса должен крепиться на высоте 12 м., а другой на земле на расстоянии 5 м. от основания мачты. Хватит ли 50м. троса для закрепления мачты? См. слайд 1.

• Учитель сообщает тему, цель и план урока.

План урока записан на доске:

1)Домашнее задание: п.54, №483, исследовательская работа.

2)Актуализация знаний.

3)Основные этапы жизнедеятельности Пифагора:

• биография;

• пифагорейский союз;

• вклад в развитие наук;

• теорема Пифагора

4)Доказательство теоремы Пифагора.

5)Решение задач.

Итог урока. Рефлексия.

II. Актуализация знаний.

• Устная работа с классом по вопросам подготовки к восприятию новой темы.

• Что называется площадью фигуры?

• Единицы измерения площади?

• Свойства площадей фигур?

• Какой треугольник называется прямоугольным?

• Как называются его стороны? (на закрытой доске рисунок)

• Чему равняется 5^2, 7^2, √64, √121, 3^2 + 5^2, 10^2 - 6^2 (это записано на скрытой доске)

III. Новая тема.

Слова учителя.

Итак, сегодня мы познакомимся с основными этапами жизнедеятельности Пифагора. Начать я хочу словами: «Знаменитый философ и ученый, религиозный и этический реформатор, полубог в глазах своих учеников и шарлатан, по отзывам иных современников. Таковы отображения Пифагора в античной литературе».

Итак, Пифагор - кто он?

(Этот урок готовился как проектная деятельность учащихся, поэтому в течение месяца учащиеся работали по группам и готовили материалы для выступления на уроке. Сейчас учитель предлагает выступить со своими сообщениями. У каждого ученика на столе лежит папка с материалами, все следят за выступлением и готовят дополнения.)

1) Выступает ученик с информацией о биографии Пифагора. См.2 слайд презентации.

2) Второй ученик рассказывает о союзе пифагорейцев. См. презентацию. Учитель делает дополнения о симметрии жизни и о пентаграмме. Читает отрывок из трагедии Гете «Фауст».

Мефистофель:

Нет, трудновато выйти мне теперь.

Тут кое-что мешает мне немного:

Волшебный знак у вашего порога.

Фауст:

Не пентаграмма ль этому виной?

Но как же, бес, пробрался ты за мной?

Каким путем впросак попался?

Мефистофель:

Изволили ее вы плохо начертить

И промежуток в уголку остался,

Там, у дверей, и я свободно мог вскочить.

3) Следующий ученик рассказывает о развитии наук в школе Пифагора.

4) Следующий ученик рассказывает о теореме Пифагора.

5) Теорема Пифагора. Выступает ученик , который приготовил самое простое доказательство теоремы и самый быстрый способ ее доказательства ( показывают прямоугольный треугольник, вырезанный из картона, катеты и гипотенузу. Затем на катетах и гипотенузе строит квадраты, показывает другую модель. Затем разрезает квадраты на треугольники, считает количество треугольников, построенных на гипотенузе и количество треугольников, построенных на катетах. Их равное количество и они равны. Делает вывод.)

Учитель читает стих о теореме.

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим.

И таким простым путем

К результату мы придем.

На этом уроке учащиеся только знакомятся с теоремой Пифагора. На следующем уроке будут рассматриваться другие способы доказательства теоремы, и делать запись в тетрадь.

IV. Решение задач.

Учащие открывают тетради, записывают число, тему, номер задачи.

Задачи даются по готовому чертежу, они записаны на скрытой доске.

№1

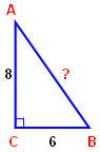
Дано: АВС, С=90 ,а=6, в=8

Найти: с



Ученик решает задачу на доске. Все записывают решение в тетрадь.



№2



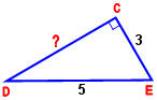
Решение на доске и в тетрадях

№3



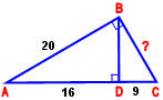
v. Итог урока

Итак, сегодня на урок мы познакомились с теоремой Пифагора, с некоторыми сведениями из жизни ученого. Решили несколько простейших задач.

Значение теоремы Пифагора состоит в том, что с ее помощью можно доказать многие теоремы геометрии решить большинство задач. На следующем уроке мы будем рассматривать доказательства теоремы, и решать более сложные задачи.

Закончить я хочу словами итальянского астронома Скиапарелли, который сказал. Что если мы хотим дать знать внеземным цивилизациям о существовании разумной жизни на земле, то следует посылать в космос изображение Пифагоровой фигуры. Эту информацию смогут принять мыслящие существа и понять, что на земле существует достаточно развитая цивилизация.

Работа по данной теме будет продолжена на следующих уроках. Один из них будет посвящен различным способам доказательства теоремы, другой решению задач.

В заключении урока прошу всех учащихся сделать рисунок в тетради.

Если вам понравился урок, было интересно, узнали много нового, чувствовали себя комфортно, то нарисуйте солнце, если урок понравился, но было беспокойство, то облако. Если не понравился, то- черные тучи и дождь.