- Учителю
- Разработка урока по теме Уравнение прямой.
Разработка урока по теме Уравнение прямой.
Геометрия - 9 класс Урок № 14
Тема: «Уравнение прямой».
Цели урока:
Образовательные:
-
вывести уравнение прямой и показать, как можно использовать это уравнение при решении геометрических задач;
-
закрепить умения и навыки по теме «Уравнение окружности»;
-
подготовка к ГИА.
Уметь:
- Распознать уравнение окружности и уравнение прямой по предложенному уравнению, научить обучающихся составлять уравнение окружности и уравнение прямой по готовому чертежу, строить окружность и прямую по заданному уравнению.
Знать:
- Формулы уравнений окружности и прямой и уметь их применять при решении задач.
Воспитательные:
- Формирование критического мышления и навыков работы в группе.
- Содействовать в ходе урока воспитанию решительности, смелости при выполнении заданий, самостоятельности.
Развивающие:
- Развитие памяти, логического мышления обучающихся при решении задач.
- Развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом.
Уметь:
- Видеть проблему и наметить пути её решения.
- Кратко излагать свои мысли устно и письменно.
Тип урока: усвоения новых знаний.
Оборудование: ПК, мультимедийный проектор, экран.
План урока.
-
Организационный момент.
Сообщение темы и целей урока. Отчет старосты класса об отсутствующих. Проверка готовности к класса к уроку.
II. Актуализация опорных знаний.
-
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
-
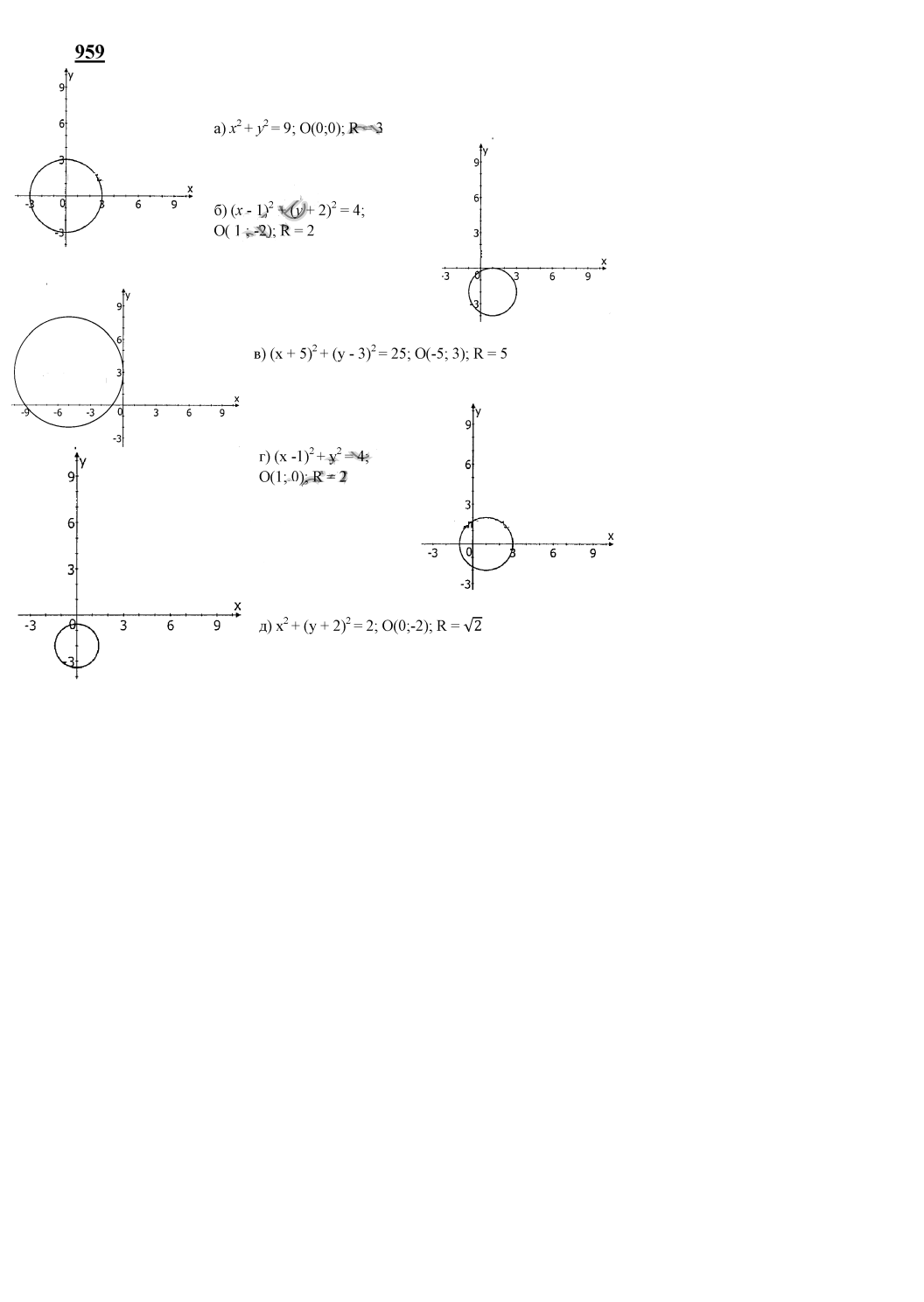
Фронтальный опрос
-
Математический диктант.
Вариант I
1. Лежит ли точка А (2; -1) на окружности, заданной уравнением (x - 2)2 + (y - 3)2 = 25?
2. Напишите уравнение окружности, если ее центр - точка (4; 5), а радиус равен 3.
3. Напишите уравнение окружности с центром в начале координат, если она проходит через точку С (-2; 3).
4. Найдите длину вектора {-12; 5}.
5. Найдите координаты середины отрезка PQ, если Р (5; -3); Q (3; -7).
6. Найдите координаты вектора , если А (2; -5), В (-3; 4).
Вариант II
1. Лежит ли точка А (2; -1) на прямой, заданной уравнением 2х - 3y - 7 = 0?
2. Напишите уравнение окружности, если ее центр - точка (4; 5), а радиус равен 2.
3. Напишите уравнение окружности с центром в точке Р (-2; -1), если она проходит через точку Q (1; 3).
4. Найдите расстояние между точками А (-1; 3) и В (2; -1).
5. Найдите координаты вектора, равного сумме векторов и, если {-12; 5}, {7; -3}.
6. Найдите координаты вектора , если С (-1; 6), D (3; -2).
III. Изучение нового материала.
Для выведения уравнения прямой проведем эту прямую как серединный перпендикуляр к некоторому отрезку с данными координатами конечных точек отрезка.
Все точки серединного перпендикуляра находятся на равных расстояниях от концов отрезка.
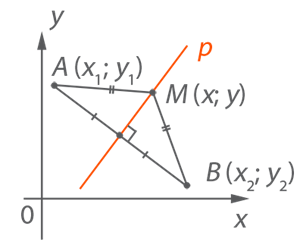
Рис. 1. Серединный перпендикуляр к отрезку
Пусть 
- это произвольная
точка на прямой 
(см. Рис. 1),
которая является серединным перпендикуляром к
отрезку 
(точка 
имеет
координаты 
, точка 
имеет
координаты 
). Тогда 
, отсюда
следует, что 
, то есть
справедливо равенство:
- это равенство и
есть уравнением прямой.
Возведем в квадрат выражения в скобках и приведем подобные слагаемые:
Введем новые обозначения:
Следовательно, уравнение прямой будет иметь следующий вид:
Уравнение вертикальной прямой
-
уравнение вертикальной прямой
На рис. 2 изображены вертикальные прямые, уравнение которых выглядят следующим образом:
а) 
. Это означает, что
все точки на этой прямой имеют координату 
.
б) 
. Это означает, что
все точки на этой прямой имеют координату 
.
в) 
. Это означает, что
все точки на этой прямой имеют координату 
, то есть это
уравнение оси 
.
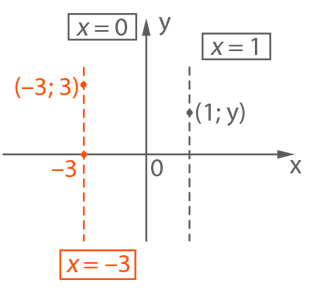
Рис. 2. Вертикальные прямые
Уравнение горизонтальной прямой
-
уравнение горизонтальной прямой
На рис. 3 изображены горизонтальные прямые, уравнения которых выглядят следующим образом:
а) 
. Это означает, что
все точки на этой прямой имеют координату 
.
б) 
. Это означает, что
все точки на этой прямой имеют координату 
.
в) 
. Это означает, что
все точки на этой прямой имеют координату 
, то есть это
уравнение оси 
.
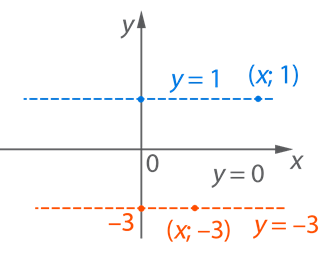
Рис. 3. Горизонтальные прямые
Уравнение наклонной прямой к оси 
()
Введем новые обозначения:
Таким образом, уравнение наклонной к оси прямой
выглядит следующим образом:
,
где
-
угловой коэффициент (если 
, то функция
возрастает, если 
- убывает);
-
ордината точки пересечения прямой с осью .
Примеры
1. Дано уравнение прямой: 
.
В этом случае 
; 
.
Следовательно, данная функция возрастает, прямая
пересекает ось 
в точке с
координатами
(см. Рис. 4).
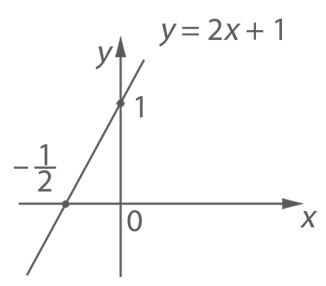
Рис. 4. Прямая
2. Дано уравнение прямой: 
.
В этом случае 
; .
Следовательно, данная функция убывает, прямая
пересекает ось в точке с
координатами (см. Рис. 5).
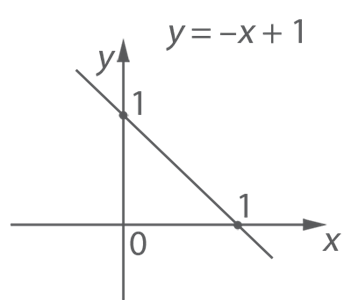
Рис. 5. Прямая
Условия параллельности и перпендикулярности наклонных прямых
Даны две прямые:
1. Данные прямые будут параллельными, если выполняются следующие условия:
То есть эти прямые должны быть наклонены под одним углом к
оси , но проходить через
разные точки на оси .
2. Данные прямые будут перпендикулярными, если выполняется следующее условие:
Уравнение прямой, проходящей через заданную точку
Дана точка 
с координатами
.
Уравнение наклонной прямой: 
, следовательно,
условие того, что точка лежит на прямой, -
это 
.
- уравнение любой
наклонной прямой, проходящей через точку 
.
Задавая коэффициент , можно выбрать
конкретную прямую, проходящую через точку.
Задача 1
Дано: прямая ; точка 
.
Найти: а) уравнение прямой, которая проходит через точку
и
параллельна заданной прямой; б) уравнение прямой,
которая проходит через точку и
перпендикулярна заданной прямой.
Решение
Все наклонные прямые, которые проходят через точку
,
имеют уравнение:
1. Угловые коэффициенты параллельных прямых равны.
Поэтому уравнение прямой, проходящей через точку и
параллельной заданной прямой, имеет угловой коэффициент
.
Следовательно, уравнение такой прямой имеет следующий
вид:
2. Произведение угловых коэффициентов
перпендикулярных прямых равно 
. Следовательно,
угловой коэффициент прямой, перпендикулярной
, равен:
Подставляем данный коэффициент в уравнение прямых,
проходящих через точку :
Ответ: а) ; б) .
Задача 2
Дано: точка 
; точка 
.
Найти: уравнение прямой и точки ее
пересечения с осями координат.
Решение
Уравнение прямой имеет вид:
Необходимо определить числа 
, 
, 
. Подставим
координаты точек и в уравнение
прямой, получим систему из двух уравнений:
Решим эту систему, выразив и через
:
Подставим это значение в равенство
:
Найденные значения и
подставляем в общее выражение прямой:
При 
разделим это
выражение на и умножим на
:
Мы получили уравнение прямой, которая проходит через
две данные точки ( и ). Запишем
это уравнение в таком виде:
Это уравнение наклонной прямой, которая имеет угловой
коэффициент и пересекает ось
в
точке с координатой (на рисунке 6 точка
).
Определим координаты точки пересечения прямой с осью
,
для этого приравняем к нулю 
:
Следовательно, координаты точки пересечения прямой
с осью - 
(на рисунке
6 точка 
).
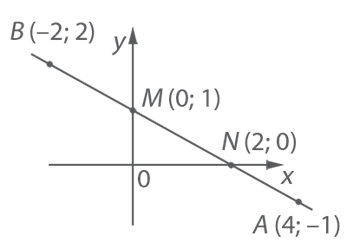
Рис. 6. Иллюстрация к задаче
Ответ: ; 
; 
.
Задача 3</</u>
Дано: точка 
; точка 
.
Найти: уравнение серединного перпендикуляра к
отрезку .
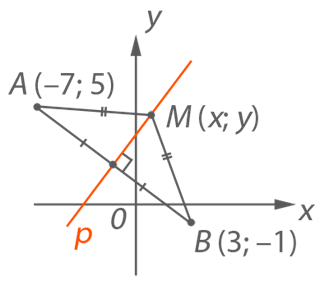
Рис. 7. Иллюстрация к задаче
Решение
Пусть (см. Рис. 7) - это
произвольная точка на серединном перпендикуляре к
отрезку . Тогда , отсюда
следует, что , то есть
справедливо равенство:
Подставим в данное равенство соответствующие координаты:
Разделим обе части уравнения на 4 и получим искомое уравнение серединного перпендикуляра:
Ответ: .
Уравнение прямой в отрезках
Пусть - уравнение
наклонной прямой, которая пересекает оси и в точках
и
.
Тогда уравнение этой прямой можно представить в виде:
Такое уравнение называется уравнением прямой в
отрезках. В данном случае отрезок 
, а отрезок
.
Пример
Дано: точка 
; точка 
.
Найти: уравнение прямой .
Решение
Уравнение прямой в отрезках выглядит следующим образом:
В данном случае: 
; 
.
Подставляем эти значения в уравнение:
Ответ: .
Уравнение прямой, проходящей через две точки.
Дано: точки 
и 
на
наклонной прямой 
(см. Рис. 11).
Требуется: вывести уравнение наклонной прямой
.
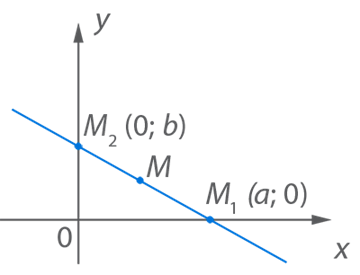
Рис. 11. Наклонная прямая, проходящая через две точки
Решение
Подставляем координаты первой точки в уравнение наклонной прямой:
Получаем систему уравнений:
Вычтем из первого уравнения второе:
Необходимо найти , для этого
подставляем координаты двух точек в уравнение наклонной
прямой:
Вычтем из первого уравнения второе:
Следовательно:
Ответ: , где 
и 
.
IV . Решение задач.
1. Учитель объясняет решение задачи:
напишите уравнение прямой, проходящей через две данные точки Р (2; 1) и Q (-3; -1).
Решение
Уравнение прямой PQ имеет вид ax + by + c = 0. Так как точки P и Q лежат на прямой PQ, то их координаты удовлетворяют этому уравнению:
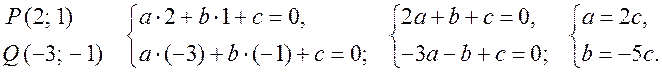
2cx - 5cy + c = 0 |: c 
0, тогда прямая PQ
задана уравнением 2x - 5y + 1 = 0.
Ответ: 2x - 5y + 1 = 0.
2. Самостоятельно по учебнику обучающиеся разбирают решение задачи № 972 (а), с. 245.
3. Решить задачу № 973 на доске и в тетрадях.
4. Решить задачу № 975.
Решение
Пересечение прямой с осью OX: y = 0, тогда 3x - 4 ∙ 0 + 12 = 0; 3x = -12; x = -4; точка А (-4; 0);
пересечение прямой с осью OY: x = 0, тогда 3 ∙ 0 - 4y + 12 = 0; -4y = -12; y = 3; точка В (0; 3).
5. Решить задачу № 976 (повторить при решении способ сложения систем уравнений):
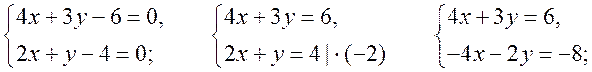
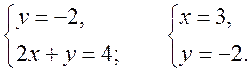
Точка пересечения прямых D (3; -2).
Ответ: (3; -2).
6. Решить задачу № 977.
Решение
Прямая, проходящая через точку М (2; 5) и параллельная оси OX, имеет вид: y = 5; прямая, параллельная оси OY, записывается уравнением: х = 2.
7. Самостоятельное решение обучающимися задачи № 978.
8. Решить устно задачи:
1) Окружность задана уравнением (x - 1)2 + y2 = 9. Назвать уравнение прямой, проходящей через ее центр и параллельной оси ординат.
Решение
Центр О (1; 0) и параллельная оси OY прямая x = 1.
2) Окружность задана уравнением (x + 1)2 + (y - 2)2 = 16. Назвать уравнение прямой, проходящей через ее центр и параллельной оси абсцисс.
Решение
Центр А (-1; 2); прямая y = 2 параллельна оси OX.
V. Подведение итогов урока.
-
С чем мы сегодня познакомились на уроке?
-
Назовите общий вид уравнения прямой.
-
Какое уравнение имеет прямая параллельная ОХ, ОУ?
VI. Домашнее задание: прочитать п. 95, ответить на вопросы с.249, выполнить № 972(а,б), № 979.
17