Технологическая карта «Задачи на шахматной доске» (интегрированное занятие по математике с применением ИКТ - технологий)

№

Этап

урока

Используемые

ЭОР

Технологии (методы, приемы)

Деятельность учителя

Деятельность обучающихся

Ожидаемый результат

1

Организационный

( 2 мин.)

Создание коллаборативной среды

а) - Посмотрите, друг другу в глаза, улыбнитесь глазками, пожелайте друг другу удачи, хорошего настроения на весь учебный день.

Б) Тренинг создания настроения и разминки пальчиков. Соприкасаются пальчиком с соседом по парте и говорят:

желаю (большой)

успеха (указательный)

большого (средний)

во всем (безымянный)

и везде (мизинец).

Здравствуй (вся ладонь).

Форма организации учебной деятельности - фронтальная

.

Стадия «Вызов» (5мин.) Цель: вызов у обучающихся уже имеющихся знаний по изучаемому вопросу; активизацию их деятельности, мотивацию к дальнейшей работе

Технология развития критического мышления, прием «инсерт»

ВЕРИТЕ ЛИ ВЫ?

ЕСЛИ ДА "V "; НЕТ "-" (Приложение 2)

1.Симметрией обладает исходное расположение шахматных фигур.

2.При каждом ходе король меняет четность хода. Например, первый ход - нечётный, второй - чётный и т.д.

3.Однако исход партии легко оценить при помощи «правила квадрата».

4.Первоначальное название шахмат - ЧАТУГАНРА.

5.Шахматная доска имеет 63 клетки

6.История шахмат началась в Древнем Вавилоне

7.Математика помогает шахматистам играть и выигрывать. А шахматы в свою очередь помогают нам решать простейшие и даже самые сложные математические задачи, помогают развивать логику, внимание и таким образом знать математику на пять.

8.Задачи на инварианты делятся на несколько типов по способу решения: в том числе и задачи на четность

Форма организации учебной деятельности - фронтальная.

Читают текст, на полях расставляют пометки (желательно карандашом, если же его нет, можно использовать полоску бумаги, которую помещают на полях вдоль текста).

Пометки должны быть следующие:

v если то, что вы читаете, соответствует тому, что вы знаете;

- если то, что вы читаете, противоречит тому, что вы уже знали, или думали, что знали;

Формируется суждение, мнение по рассматриваемому вопросу

Представление знаний по рассматриваемому вопросу в виде графического изображения.

2

Стадия осмысления

Цель:

-сохранение

интереса к теме при

непосредственной

работе с

информацией;

ЭОР №1. (из президентской библиотеки им. Ельцина)

Блокнот

MimioStudio.

Блокнот MimioStudio.

ЭОР 2

ЭОР 3

СОЗДАНИЕ МИНИ ПРОЕКТОВ

Предлагает выяснить какие из высказываний являются истиной.

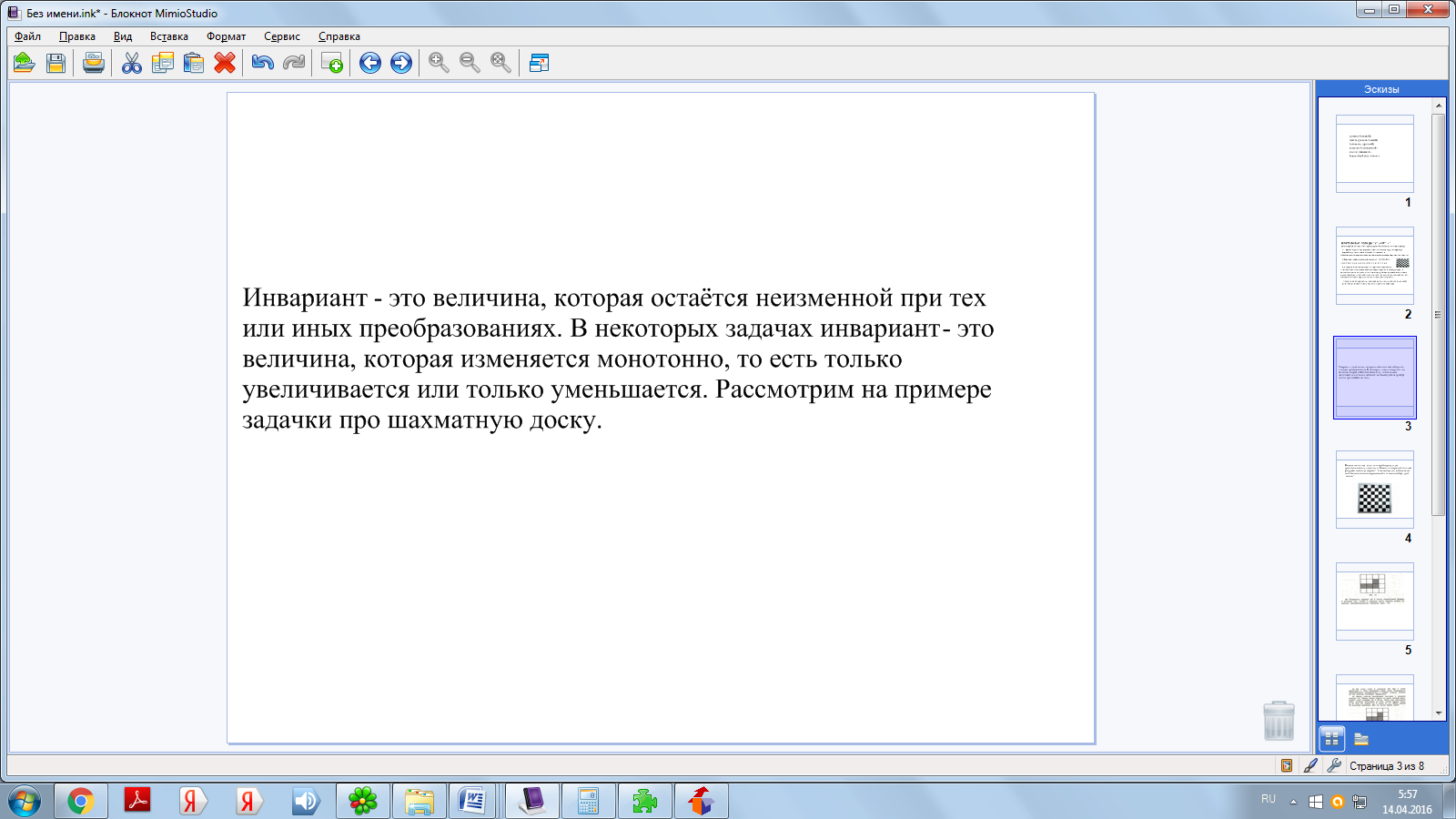
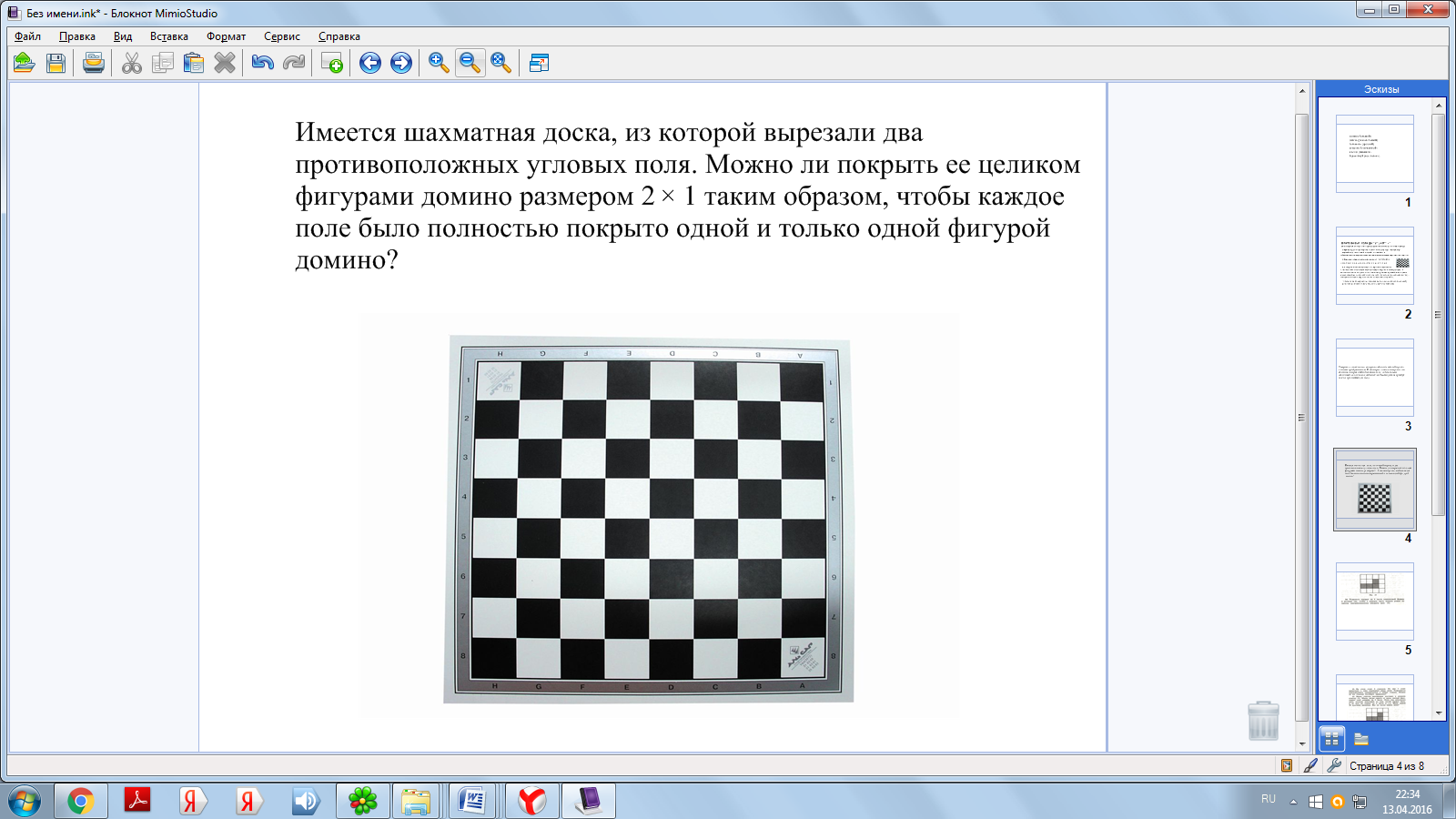
Инвариант - это величина, которая остаётся неизменной при тех или иных преобразованиях. В некоторых задачах инвариант - это величина, которая изменяется монотонно, то есть только увеличивается или только уменьшается. Рассмотрим на примере задачки про шахматную доску.

(Приложение 3)

Решают задачи на инвариант на примере шахматной доски.

(Приложение 4)

Организует работу в группах.

1группа - выполнив верно задание узнает первоначальное название шахмат (ПРИЛОЖЕНИЕ 5 )

2 группа - выполнив верно задание узнает в какой стране началась история шахмат (ПРИЛОЖЕНИЕ 6 )

3 Группа -выполнив верно задание проверит истину следующи высказываний: а)Симметрией обладает исходное расположение шахматных фигур.

Б).При каждом ходе король меняет четность хода. Например, первый ход - нечётный, второй - чётный и т.д.(ПРИЛОЖЕНИЕ 7)

4 группа -выполнив верно задания, узнает сколько клеток на шахматной доске (ПРИЛОЖЕНИЕ 8 ) и

(ПРИЛОЖЕНИЕ ЭОР 2)

- (ПРИЛОЖЕНИЕ ЭОР 3 )

5 группа выполнив верно задания узнает о взаимосвязи шахмат и математики

По мере выполнения

Заданий учащимся выдаются карточки с информацией (ПИЛОЖЕНИЕ 9)

Работают с толковым словарём, находят значение слова «Шахматы», «Инвариант»

Ставят вопросы, решают задачи, думают над оформлением своей полосы листовки

в процессе группового обсуждения обеспечивать обмен знаниями между членами группы для принятия эффективных совместных решений, в совместной деятельности.

3.

Стадия рефлексия.

Цель:формирование личностного отношения к информации

Технология развития критического мышления, прием

Обеспечивает обратную связь.

Создание группой своей полосы газеты « Шахматы».

А сейчас, ребята, вы в каждой группе выпустите свою полосу газеты. Обязательно используйте ту информацию, которая вас впечатлила, запишите решение к выбранной задаче, а также можно использовать вырезки из газет, ваши личные истории. Затем руководитель каждой группы со своими помощниками расскажет о своём выборе.

Переосмысление собственных представлений с учетом вновь приобретенных знаний

Резюмирование информации

4

Итоги урока

Организует подведение итогов по обработанной информации.

Организует каждую из пяти групп на создание своей полосы в газете

Работают в группах. Вы-пускают полосы газет, наполняя её выбранной информацией. Каждая группа презентует свою полосу газеты

Достижение цели урока; получение новых знаний

ПРИЛОЖЕНИЕ 1

ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР

просмотр контента в режиме 2D Silverlight

www.prlib.ru/elfapps/pageturner2d/viewer.aspx?orderdate=13.04.2016&DocUNC_ID=32884&Token=nx0VWUg3hix/7AAZdClG+w==〈=ru-RU

2

Математика / Деление десятичных дробей на натуральные числа. Деление на десятичную дробь. Умножение и деление десятичной дроби на 0,1; 0,01; 0,001 и т.д.

ИР сферы образования

информационный модуль

ОМС МОДУЛЬ

fcior.edu.ru/card/12882/zadanie-v-kartinkah-po-teme-tekstovaya-zadacha-predpolagayushchaya-deystviya-s-desyatichnymi-drobyami-k1.html

3

Математика / Деление десятичных дробей на натуральные числа. Деление на десятичную дробь. Умножение и деление десятичной дроби на 0,1; 0,01; 0,001 и

Тип ИР сферы образования

информационный модуль

ОМС МОДУЛЬ

fcior.edu.ru/card/8790/zadanie-v-kartinkah-po-teme-umnozhenie-i-delenie-desyatichnoy-drobi-na-razryadnuyu-edinicu-10-100-1000-0-1-0-01-i-t-d-k2.html</</p>

ПРИЛОЖЕНИЕ 2

ВЕРИТЕ ЛИ ВЫ? ЕСЛИ ДА "V " ; НЕТ "-" (Приложение 2)

1.Симметрией обладает исходное расположение шахматных фигур.

2.При каждом ходе король меняет четность хода. Например, первый ход - нечётный, второй - чётный и т.д.

3.Однако исход партии легко оценить при помощи «правила квадрата».

4.Первоначальное название шахмат - ЧАТУГАНРА.

5.Шахматная доска имеет 63 клетки

6.История шахмат началась в Древнем Вавилоне

7.Математика помогает шахматистам играть и выигрывать. А шахматы в свою очередь помогают нам решать простейшие и даже самые сложные математические задачи, помогают развивать логику, внимание и таким образом знать математику на пять.8.Задачи на инварианты делятся на несколько типов по способу решения: в том числе и задачи на четность

ПРИЛОЖЕНИЕ 3

ПРИЛОЖЕНИЕ 4

ПРИЛОЖЕНИЕ 5

1.

6,5 - 2,1 = (А)

4,5 - 2,2 = (Ч)

7,3 - 3 = (Т)

8,9 - 5,6 = (Р)

7 - 1,5 = (Г)

6,3 - 2,2 = (У)

3,8 - 2,5 = (Н)

ПРИЛОЖЕНИЕ 6

2.Кто же придумал эту увлекательную игру?

Есть такая легенда. Много сотен лет назад народ этой страны страдал от бесконечных кровавых битв между армиями воинственных и жестоких правителей. Чтобы помочь людям, мудрецы придумали шахматы. Они говорили: если хотите воевать друг с другом, то вот вам доска - поле боя, вот фигуры - офицеры и солдаты, конница, боевые слоны и колесницы. Вот вам честные правила борьбы. Зачем убивать друг друга? Лучше воевать на шахматных досках. Люди согласились с этим, и в страну пришел мир.

21,3 - 9,6 = (Д)

30,5+ 18,9 =(И)

40,7 - 31,8 = (Н)

80 - 63,5 = (Я)

3.Найдите:

Белые - площадь фигуры. S = a ∙ b

Черные - периметр фигуры P = (a + b) ∙ 2

ПРИЛОЖЕНИЕ 7

Найдите названия шахматных фигур, зашифрованных в таблице и выполните верную расстановку

ПРИЛОЖЕНИЕ 8

5. 64

- Какое это число?

- Сколько десятков и единиц?

- Представьте в виде суммы разрядных слагаемых.

- Уменьшите 64 на 6 десятков, на 4 единицы.

- На сколько 64 больше 60, на сколько 64 меньше 4.

- Назовите соседей числа 64.

- Какие числа можно составить используя цифры 6 и 4?

ПРИЛОЖЕНИЕ 9

Симметрией обладает исходное расположение шахматных фигур.

Известна такая забавная история. Некто явился в шахматный клуб и объявил, что нашел верный способ не проигрывать черными. «Каким образом?» - спросили его. «Очень просто, - ответил гость, - повторяя ходы противника!» Сыграть с наивным изобретателем вызвался С.Ллойд, который и объявил ему мат в 4 хода. Неясно, как Ллойд это сделал. Я могу поставить мат за 6 ходов при полной симметрии фигур.

Четность и нечетность

Число - одно из основных понятий математики, позволяющее выразить результаты счета или измерения. Со временем люди научились не только называть числа, но и обозначать их цифрами (условные знаки для обозначения чисел).

Цифры 2, 4, 6, 8 называются четными, а цифры 1, 3, 5, 7, 9 нечетными. Из признака делимости на 2 следует, что натуральные числа, которые делятся на 2, называются четными, остальные - нечетными.

На шахматной доске так же есть чётность и нечётность. Тут они связаны с номером хода.

При каждом ходе король меняет четность хода. Например, первый ход - нечётный, второй - чётный и т.д.

Можно сказать, что ничего удивительного и интересного здесь нет. Можно подумать, что при виде шахматной доски мы сразу вспоминаем геометрию (из - за геометрической формы доски). Это, безусловно, так, но геометрическая форма ещё не всё.

Дело в том, что при игре в шахматы, как и в любой другой науке, есть свои определённые правила. И существует такое правило, как правило, квадрата.

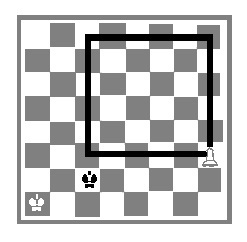
Квадратом называется прямоугольник, у которого все стороны равны. При этой композиции (Рис.8) неопытные шахматисты рассуждают так: пешка идет сюда, король туда, пешка сюда, король туда и т.д. и при этом они часто путаются и, в конце концов, просчитываются.

Правило квадрата

Однако исход партии легко оценить при помощи «правила квадрата».

Достаточно выяснить, может ли король при своем ходе попасть в квадрат пешки. Итак, в нашей композиции черные при ходе делают ничью (попадают в квадрат), а при ходе противника проигрывают.

Существует связь между шахматами и математикой. Математика помогает шахматистам играть и выигрывать. А шахматы в свою очередь помогают нам решать простейшие и даже самые сложные математические задачи, помогают развивать логику, внимание и таким образом знать математику на пять.