Методическая разработка по математике для 8 - 11 классов «Решим квадратное уравнение устно!»

Методическая разработка

по математике:

«Решим квадратное уравнение УСТНО!».

Для учащихся 8 - 11 классов.

Полные квадратные уравнения ax² + bx + c = 0.

1.Свойство коэффициентов.

а) Если в квадратном уравнении ax² + bx + c = 0 выполняется условие:

a + b + c = 0, то x₁ = 1, x₂ = .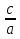

Пример. 2x² - 9x + 7 = 0.

Так как 2 - 9 + 7 = 0, то x₁= 1, x₂ = .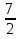

б) Если в квадратном уравнении ax² + bx + c = 0 выполняется условие:

a + c = b, то x₁ = - 1, x₂ = - .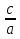

Пример. 2x² + 9x + 7 = 0.

Так как 2 + 7 = 9, то x₁= - 1, x₂ = - .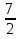

2. Связь между коэффициентами. (А)

1) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = m² + 1, c = m, m > 0, то

x₁= - m, x₂ = - .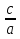

Пример. 3x² + 10x + 3 = 0.

m = 3; 10 = 3² + 1= m² + 1.

x₁= - 3, x₂ = - .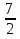

2) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = - (m² + 1), c = m, m > 0, то

x₁= m, x₂ = .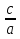

Пример. 4x² - 17x + 4 = 0.

m = 4; - 17 = - (4² +1) = - (m² + 1)

x₁= 4 , x₂ = .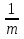

3) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = m² - 1, c = - m, m > 0, то

x₁= - m, x₂ = .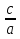

Пример. 3x² + 8x - 3 = 0.

m = 3; 8 = 3² - 1 = m² - 1

x₁= - 3, x₂ = .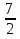

4) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = - (m² - 1), c = - m, m > 0, то

x₁= m, x₂ = - .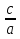

Пример. 4x² - 15x - 4 = 0.

m = 4; - 15 = - (4² -1) = - (m² - 1)

x₁= 4 , x₂ = - .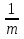

3. Связь между коэффициентами. (Б)

1) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = m³ + 1, c = m², m > 0, то

x₁= - m², x₂ = - .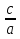

Пример. 3x² + 28x + 9 = 0.

m = 3; 28 = 3³ +1 = m³ + 1; 9 = 3² = m².

x₁= - 9, x₂ = - .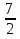

2) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = - (m³ + 1), c = m², m > 0, то

x₁= m², x₂ = .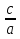

Пример. 4x² - 65x + 16 = 0.

m = 4; - 65 = - (4³ +1) = - (m³ + 1); 16 = 4² = m².

x₁= 16 , x₂ = .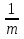

3) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = m³ - 1, c = - m², m > 0, то

x₁= - m², x₂ = .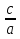

Пример. 3x² + 26x - 9 = 0.

m = 3; 26 = 3² -1 = m³ - 1; - 9 = - 3² = - m².

x₁= - 9, x₂ = .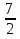

4) Если в квадратном уравнении ax² + bx + c = 0: a = m, b = - (m³ - 1), c = - m², m > 0, то

x₁= m², x₂ = - .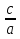

Пример. 4x² - 63x - 16 = 0.

m = 4; - 63 = - (4³ - 1) = - (m³ - 1); - 16 = - 4² = - m².

x₁= 16 , x₂ = - .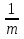

4. Связь между коэффициентами. (В)

1) Если в квадратном уравнении ax² + bx + c = 0: a = m², b = m³ + 1, c = m, m > 0, то

x₁= - m, x₂ = - .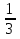

Пример. 9x² + 28x + 3 = 0.

m = 3; 9 = 3² = m²; 28 = 3³ + 1 = m³ + 1.

x₁= - 3, x₂ = - .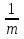

2) Если в квадратном уравнении ax² + bx + c = 0: a = m², b = - (m³ + 1), c = m, m > 0, то

x₁= m, x₂ = .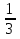

Пример. 16x² - 65x + 4 = 0.

m = 4; 16 = 4² = m²; - 65 = - ( 4³ + 1) = - (m³ + 1).

x₁= 4, x₂ = .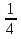

3) Если в квадратном уравнении ax² + bx + c = 0: a = m², b = m³ - 1, c = - m, m > 0, то

x₁= - m, x₂ = .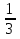

Пример. 9x² + 26x - 3 = 0.

m = 3; 9 = 3² = m²; 26 = 3³ -1 = m³ - 1.

x₁= - 3, x₂ = .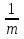

4) Если в квадратном уравнении ax² + bx + c = 0: a = m², b = - (m³ - 1), c = - m, m > 0, то

x₁= m, x₂ = - .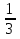

Пример. 16x² - 63x - 4 = 0.

m = 4; 16 = 4²; - 63 = - (4³ - 1) = - ( m³ - 1).

x₁= 4 , x₂ = - .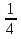

5. Связь между коэффициентами. (Г)

1) Если в квадратном уравнении ax² + bx + c = 0: a = m∙n, b = m² + n², c = m∙n, m > 0,n > 0, то

x₁= - 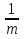, x₂ = - .

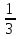Пример. 12x² + 25x + 12 = 0.

m = 3, n = 4; 12 = 3∙4 = m∙n; 25 = 9 + 16 = 3² + 4² = m² + n² .

x₁= - 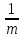, x₂ = - .

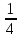2) Если в квадратном уравнении ax² + bx + c = 0: a = m∙n, b = - (m² + n²), c = m∙n, m > 0, n > 0, то

x₁= 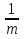, x₂ = .

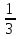Пример. 12x² - 25x + 12 = 0.

m = 3, n = 4; 12 = 3∙4 = m∙n; - 25 = - (9 + 16) = - (3² + 4²) = - (m² + n²).

x₁= 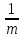, x₂ = .

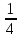3) Если в квадратном уравнении ax² + bx + c = 0: a = m∙n, b = m² - n², c = - m∙n, m > 0,n > 0, то

x₁= - 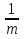, x₂ = .

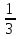Пример. 6x² + 5x - 6 = 0.

m = 3, n = 2; 6 = 3∙2= m∙n, 5 = 9 - 4 = 3² - 2² = m² - n².

x₁= - 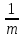, x₂ = .

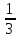4) Если в квадратном уравнении ax² + bx + c = 0: a = m∙n, b = - (m² - n²), c = - m∙n, m > 0,n > 0, то x₁= 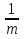, x₂ = - .

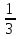Пример. 6x² - 5x - 6 = 0.

m = 3, n = 2; 6 = 3∙2 = m∙n, - 5 = - (9 - 4) = - (3² - 2²) = - (m² - n²).

x₁= 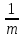, x₂ = - .

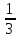6.Использование формулы квадрата суммы (разности):

(a ± b)² = a² ± 2ab + b².

Пример. 4x² - 12x + 9 = 0.

(2х - 3)² = 0, 2х - 3 = 0, 2х = 3, х = 1,5.

Пример. 4х² + 20х + 25 = 0.

(2х + 5)² = 0, 2х + 5 = 0, 2х = -5, х = -2,5.

Приведенные квадратные уравнения x² + px + q = 0.

1.Решение уравнений по теореме, обратной теореме Виета.

Между корнями и коэффициентами приведенного квадратного уравнения х² + рх + q = 0 существует следующая связь:

Если числа х₁ и х₂ таковы, что х₁ + х₂ = - p, х₁х₂ = q, то х₁ и х₂ - корни уравнения.

Познакомили поэта
С теоремою Виета.
Оба корня он сложил,
Минус «пэ» он получил,
А корней произведение
Дает «ку» из уравнения.

По коэффициентам можно предсказать знаки корней:

1) Если свободный член приведенного квадратного уравнения положителен, то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента: при положительном р корни отрицательные, при отрицательном р корни положительные.

а) Если q > 0 и р > 0 , то оба корня отрицательны.

Пример. х² + 8х + 7 = 0.

х₁х₂ = 7, х₁ + х₂ = - 8,

х₁ = - 1, х₂ = - 7.

б) Если q > 0 и р < 0, то оба корня положительные.

Пример. х² - 8х + 7 = 0.

х₁х₂ = 7, х₁ + х₂ = 8,

х₁ = 1, х₂ = 7.

2) Если свободный член приведенного квадратного уравнения отрицателен, то уравнение имеет два различных по знаку корня, знак меньшего по модулю корня совпадает со знаком второго коэффициента в уравнении.

а) Если q < 0 и р > 0 , то меньший по модулю корень будет положителен.

Пример. х² + 8х - 9 = 0.

х₁х₂ = - 9, х₁ + х₂ = - 8,

х₁ = 1, х₂ = - 9.

б) Если q < 0 и р < 0, то меньший по модулю корень будет отрицателен.

Пример. х² - 8х - 9 = 0.

х₁х₂ = -9, х₁ + х₂ = 8,

х₁ = - 1, х₂ = 9.

Замечание. Зная, что при сложении чисел с разными знаками их модули вычитаются, то для нахождения корней приведенного уравнения необходимо выполнить следующие действия:

1) найти такие пары делителей числа q, чтобы их разность была равна числу р,

2) поставить пред меньшим из найденных чисел второй знак уравнения, другой корень будет иметь противоположный знак.

Пример. х² - 2х - 15 = 0.

Из пар делителей числа 15 (1 и 15, 3 и 5) выбираем ту, разность которых равна 2. Это числа 3 и 5. Перед меньшим числом ставим знак второго коэффициента уравнения, т. е. "минус".

Таким образом, х₁ = - 3, х₂ = 5.

Такой алгоритм помогает очень быстро решать уравнения тем учащимся, у которых имеются проблемы с подобным знаком в теореме Виета.

2.Свойство коэффициентов.

Для коэффициентов уравнения вида х² + рх + q = 0 имеет место следующие соотношения:

1) если 1+ p + q = 0, то x₁ = 1, x₂ = q .

Пример. х² - 8х + 7 = 0.

Так как 1 + (- 8) + 7 = 0, то х₁ = 1, х₂ = 7.

2) если 1 + q = p, то x₁ = - 1, x₂ = - q .

Пример. х² + 8х + 7 = 0.

Так как 1 + 7 = 8, то х₁ = - 1, х₂ = - 7.

3. Связь между коэффициентами. (А)

1) Если в квадратном уравнении х² + рх + q = 0: q = 1, p = 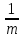, m > 0,

то х₁ = - m, х₂ = -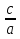. (Оба корня отрицательны).

Пример. х² + 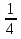х + 1 = 0.

m = 3; p = = = .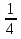

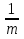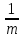х₁= - 3, х₂ = - .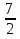

2) Если в квадратном уравнении х² + рх + q = 0: q = 1, p = -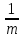, m > 0,

то х₁ = m, х₂ = 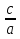. (Оба корня положительны).

Пример. х² - 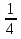х + 1 = 0.

m = 3; p = - = - = .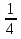

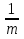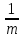х₁ = 3, х₂ = .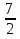

3) Если в квадратном уравнении х² + рх + q = 0: q = - 1, p = 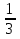, m > 0,

то х₁ = - m, х₂ = 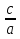. (Корни разных знаков).

Пример. х² + 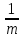х - 1 = 0.

m = 3; p = = = .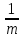

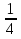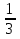х₁= - 3, х₂ = .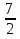

4) Если в квадратном уравнении х² + рх + q = 0: q = - 1, p = - 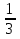, m > 0,

то х₁ = m, х₂ = - 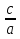. (Корни разных знаков).

Пример. х² - 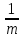х - 1 = 0.

m = 3; p = - = - = - .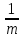

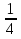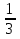х₁= 3, х₂ = - .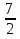

4.Связь между коэффициентами. (Б)

1) Если в квадратном уравнении х² + рх + q = 0: q = m, p = 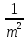, m > 0,

то х₁ = - m², х₂ = -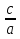. (Оба корня отрицательны).

Пример. х² + 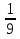х + 5 = 0.

m = 5; p = = = .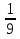

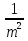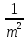х₁= - 25, х₂ = - .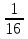

2) Если в квадратном уравнении х² + рх + q = 0: q = m, p = - 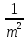, m > 0,

то х₁ = m², х₂ = 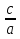. (Оба корня положительные).

Пример. х² - 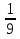х + 5 = 0.

m = 5; p = - = - = - .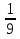

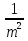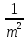х₁= 25, х₂ = .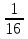

3) Если в квадратном уравнении х² + рх + q = 0: q = - m, p = 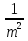, m > 0,

то х₁ = - m², х₂ = 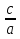. (Корни разных знаков).

Пример. х² + 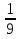х - 5 = 0.

m = 5; p = = = .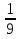

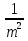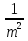х₁= - 25, х₂ = .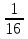

4) Если в квадратном уравнении х² + рх + q = 0: q = - m, p = - 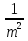, m > 0,

то х₁ = m², х₂ = - 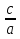. (Корни разных знаков).

Пример. х² - 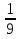х - 5 = 0.

m = 5; p = - = - = - .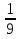

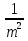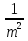х₁= 25, х₂ = - .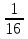

5.Связь между коэффициентами. (В)

1) Если в квадратном уравнении х² + рх + q = 0: q = 1, p=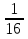, m > 0,n > 0, то

x₁= - 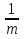, x₂ = - .

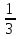Пример. x² + 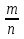x + 1 = 0.

m = 3, n = 4; 12 = 3∙4 =m∙n; 25 = 9 + 16 = 3² + 4² = m² + n², p == .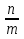

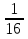x₁= - 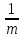, x₂ = - .

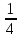2) Если в квадратном уравнении х² + рх + q = 0: q = 1, p = - 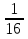, m > 0,n > 0, то

x₁= 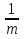, x₂ = .

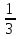Пример. x² - 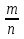x + 1 = 0.

m = 3, n = 4; 12 = 3∙4 = m∙n; - 25 = - (9 + 16) = - (3² + 4²) = - (m² + n²), p = - = -.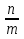

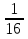x₁= 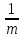, x₂ = .

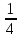3) Если в квадратном уравнении х² + рх + q = 0: q = - 1, p = 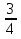, m > 0,n > 0, то

x₁= - 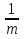, x₂ = .

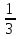Пример. x² + 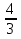x - 1 = 0.

m = 3, n = 2; 6 = 3∙2 =m∙n, 5 = 9 - 4 = 3² - 2² = m² - n², p = = .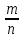

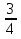x₁= - 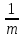, x₂ = .

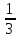4) Если в квадратном уравнении х² + рх + q = 0: q = -1, p= - (m² - n²), m > 0,n > 0, то x₁= 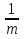, x₂ = - .

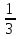Пример. x² - 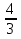x - 1 = 0.

m = 3, n = 2; 6 = 3∙2 = m∙n, - 5 = - (9 - 4) = - (3² - 2²) =- (m² - n²), p = - =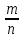

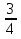
x₁= 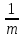, x₂ = - .

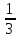6.Использование формулы квадрата суммы (разности):

(a ± b)² = a² ± 2ab + b².

Пример. 1) х² + 10х + 25 = 0.

(х + 5)² = 0, х + 5 = 0, х = -5.

Пример. 1) х² - 8х + 16 = 0.

(х - 4)² = 0, х - 4 = 0, х = 4.

6.Метод переброски.

Так называемый метод «переброски» позволяет сводить решение неприведённых и непреобразуемых к виду приведённых с целыми коэффициентами путём их деления на старший коэффициент уравнений к решению приведённых с целыми коэффициентами. Он заключается в следующем:

1) умножаем обе части уравнения на а:

ах²+ bх + с = 0 | ∙а

(ах)²+ bах + ас = 0.

2) вводим новую переменную y = ax, получаем уравнение: у² + bу + ас = 0.

Происходит «переброска» старшего коэффициента а к свободному члену с.

3) решая приведенное уравнение, находим корни у₁ и у₂.

4) возвращаясь к переменной х, имеем: x₁ = 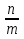, x₂ = .

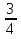Пример. 2х² - 9х + 7 = 0.

«Перебросим» коэффициент 2 к свободному члену:

у² - 9у + 14 = 0.

Согласно теореме, обратной теореме Виета у₁= 2 и у₂ = 7.

Следовательно: x₁ = 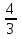= 1, x₂ = 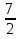= 3,5.

Неполные квадратные уравнения.

1) ax² + c = 0.

ax² = - c, x² = - 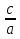. Пусть - 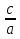= d, тогда имеем уравнение вида: x² = d.

Если d > 0, то уравнение имеет два корня: x₁ = + 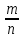_, x₂ = -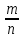

Если d < 0, то уравнение не имеет корней.

Пример. 2x² + 5 = 0.

2x² = - 5; x² = -2,5 - корней нет.

Пример. 2x² - 14 = 0.

2x² =14; x² =7; x_1,2 = ± .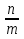

Частный случай (применение формулы разности квадратов: a² - b² = (a - b)(a + b)).

Пример. x² - 49 = 0.

(x - 7)(x + 7) = 0; x - 7 = 0 или x + 7 = 0; x₁ = 7 или x₂ = - 7.

2) ax² + bx = 0.

x (ax + b) = 0; x = 0 или ax +b = 0, откуда x₁ = 0 или x₂ = -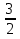

Пример.1) 2x² - 5x = 0.

x (2x - 5) = 0; x = 0 или 2x - 5 = 0, откуда x₁ = 0 или x₂ = - 2,5.

3) ax² = 0.

x² = 0; x = 0

Литература.

1.Мордкович А.Г.Алгебра 8 класс. М., Мнемозина, 2010.

2.Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. - М., высшая школа, 1969.

3. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. - М., Просвещение, 1972.

Интернет- ресурсы:

http://www.zavuch.info/methodlib/358/75891/