- Учителю
- Элективный курс Теория чисел
Элективный курс Теория чисел
«Теория чисел»
элективный курс для школьников
Пояснительная записка
Актуальность курса определяется значимостью понимания школьниками особого положения теории чисел в школьной программе. Но программа школьного курса ограничена и не позволяет в полном объеме рассмотреть задачи на использования алгоритма Евклида при нахождении НОД и решении диофантовых уравнений, также подробного рассмотрения фигурных, простых и составных, дружественных, совершенных чисел. Эти задачи часто включаются в письменные работы при поступлении в различные учебные заведения и вызывают у учащихся трудности, обусловленные необходимостью понимания закономерностей, наличия навыка анализа конкретного случая на основе известных общих свойств объекта, систематичности и последовательности в решении, умения объединять рассмотренные частные случаи в единый результат. Разрешить трудности учащихся и рассмотреть вышеназванные задачи может данный элективный курс «Теория чисел».
Место и роль курса в образовательном процессе.
Курс «Теория чисел» предназначен для предпрофильной подготовки школьников, для реализации в 9 классе. Он, с одной стороны, поддерживает изучение основного курса алгебры, направлен на систематизацию знаний, реализацию внутрипредметных связей, а с другой - служит для построения индивидуального образовательного пути. Курс формирует такие умения и навыки как логичность и самостоятельность мышления, умение обобщать и систематизировать, навыки в решении задач.
Предлагаемый курс, как и любой другой, улучшает имидж и повышает конкурентоспособность школы, так как реализация данного курса дает более глубокие знания по математике, увеличивает уровень интеллектуального развития учащихся, что благоприятствует их дальнейшему обучению.
При реализации курса будут созданы условия для того, чтобы ученик утвердился или отказался от сделанного им выбора направления дальнейшего учения и деятельности в области «Математика». А именно, при систематическом и более глубоком изучении тем ученик поймет, способен ли он заниматься изучением математики (решать более сложные задачи, чем предполагает школьная программа, рассматривать разные варианты решения одной и той же задачи, находить решение нестандартных задач и т.д.) и хочет ли он это делать.
Цель курса: перейти от репродуктивного уровня усвоения материала (простого решения задач) к творческому; научить применять знания алгоритма Евклида, свойств простых и составных, дружественных, фигурных, совершенных чисел, Пифагоровых троек, составление диофантовых уравнений при решении задач, а также применение предметной проектной деятельности и создание тематических презентаций учащимися.
Задачи курса:
·углубить и расширить знания по алгебре;
·предоставить ученику возможность реализовать свой интерес к выбранному предмету, определить готовность ученика осваивать выбранный предмет на повышенном уровне;
·видеть фигурные, простые, составные, совершенные и дружественные числа и уметь использовать их свойства для решения задач;
·уметь применять алгоритм Евклида при нахождении НОД ;
уметь решать диофантовы уравнения.
По типу данный курс является предметным, главная задача которого состоит в расширении знаний по алгебре.
Мотивами для выбора данного курса у учеников могут быть следующие:
-
подготовка к выпускным и вступительным экзаменам;
-
поддержка изучения базового курса математики;
-
любопытство;
-
заинтересованность математикой;
-
профессиональная ориентация.
Требования, которым отвечает тематика и содержание курса:
-
поддержание изучения базового курса алгебры;
-
социальная и личностная значимость: повышается уровень образованности школьников, расширяется их кругозор, удовлетворяются познавательные интересы в области математики;
-
обладание значительным развивающим потенциалом (развитие математического мышления, умения систематизировать, обобщать, делать выводы).
Данный курс предусматривает использование классно-урочной и лекционно-практической систем, а также личностно-ориентированных педагогических технологий. При решении задач значительное место должны занимать поиски идей решения, эвристические соображения, и только затем, само решение, найденное эвристически, проводится строгим логическим рассуждением.
Теоретическую часть материала предполагается излагать в форме лекции. На всех практических занятиях должна присутствовать самостоятельная работа учащихся: индивидуально, в парах, в группах - в зависимости от уровня обучаемости школьников. Также предусматривается работа с литературой, работа в компьютерном классе, публичные выступления, проектная деятельность. Такая организация способствует реализации развивающих целей курса, так как развитие способностей учащихся возможно лишь при сознательном, активном участии в работе самих учащихся.
Содержание курса может быть освоено как в коллективных, так и в индивидуально-групповых формах. Данная разработка предполагает освоение курса в коллективной форме.
Ожидаемый результат изучения курса:
-
умение самостоятельно добывать информацию и осознанно ее использовать при выполнении заданий;
-
приобретение опыта в нахождении правильного и рационального пути решения задачи;
-
практика работы в группе: умение распределять обязанности, учитывать мнение каждого члена группы, адекватно оценивать работу товарищей (при условии коллективной формы организации обучения).
Использование на уроках математики современных ИКТ позволяет моделировать различные уровни учебного процесса, к которым школьнику необходимо адаптироваться, формирует положительную мотивацию к изучению данного предмета, формирует компетенции в области ИКТ.
Одним из результатов освоения курса может быть осознанный выбор учащимся других элективных математических курсов при профильном обучении.
Система форм контроля уровня достижений учащихся и критерии оценки:
I. Формы промежуточного контроля: письменные задания по материалу; проверка домашнего задания; взаимоконтроль; устный ответ ученика; тематическая презентация; компьютерный мониторинг.
На занятиях ученики будут получать баллы, выставляемые в табель баллов каждого
«Теория чисел» (34 часов)
Табель баллов ………………………………………………….. (Ф.И.)
№ занятия
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Баллы
№ занятия
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Баллы
№ занятия
29
30
31
32
33
34
Баллы
Общий итог:
Все набранные учеником баллы по окончанию курса суммируются, и выясняется, как школьник усвоил программу данного курса.
II. Форма итоговой работы - зачетная работа, состоящая из трех блоков:
А - задания с выбором вариантов ответа; В - задания с краткой записью ответа;
С - задания, предполагающие развернутый ответ.
Предлагаемый курс рассчитан на 34 часа. Он может быть использован как отдельный элективный курс, с одной стороны, и для расширения и углубления ЗУНов, с другой - при изучении профильного курса математики и наличии дополнительного времени на его изучение.
Программа построена таким образом, что учитель сам может решать, сколько и какие темы в неё включить в зависимости от уровня подготовленности учащихся. Темы содержательной части программы расположены по нарастающей степени сложности и трудности, при этом учитель вправе ограничиться подбором таких заданий практического содержания, которые будут доступны всем учащимся и одновременно повысят уровень их математических знаний и создадут необходимый уровень знаний для продолжения изучения математики в 10 классе математического профиля. Данный элективный курс может быть использован учителем и в старших 10-11 классах для развития и систематизации знаний учащихся по теме и подготовки их к итоговой аттестации, выпускным экзаменам в школе и вступительным испытаниям в вузы.
Для данного курса не предполагается разработка учебного пособия для учащихся и рабочей тетради. Для самостоятельного и более подробного изучения курса школьниками используется аннотированный список литературы, подготовленный к каждой теме. Задания для самостоятельной работы учащихся предоставляют разработки занятий, представленные ниже. Также задания можно брать из литературы, указанной в конце программы.
В качестве методических рекомендаций при подготовке к занятиям учитель может использовать предложенные ниже разработки занятий элективного курса.
Содержание изучаемого курса
1.Теория чисел.Нумерология. Задачи Пифагора. Фигурные числа.
2.Операции над целыми числами. Представление целых чисел с помощью письменных знаков (нумерация).
3.Магические квадраты.
4. Простые и составные числа. Основная теорема о разложении на множители. Решето Эратосфена. Совершенные числа. Дружественные числа.
5. Наибольший общий делитель (НОД). Взаимно простые числа. Алгоритм Евклида. Наименьшее общее кратное (НОК).
6. Диофантовы уравнения.
7. Игры с числами.
Учебно-тематический план 1-3
4
5
Теория чисел. Нумерология.
Задача Пифагора.
Фигурные числа.
3
1
1
2
0,5
0,5
1
0,5
0,5
6-7
Магические квадраты
2
0.5
1.5
8-15
Решето Эратосфена.
Простые и составные числа.
Основная теорема о разложении на множители
Совершенные числа.
Дружественные числа
8
3,5
4,5
16-17
Наибольший общий делитель (НОД)
Взаимно простые числа
2
0.5
1.5
18-19
Алгоритм Евклида
2
1
1
20
Наименьшее общее кратное
1
0.5
0.5
21-22
Зачет
2
2
23-30
Уравнения в целых числах.
8
3
5
31-32
Зачет
2
2
33-34
Конференция
2
2
Итого часов:
34
12
22
Календарно-тематический план
|
|
Алгоритм Евклида |
1 |
12.01 |
|
|
|
Алгоритм Евклида |
1 |
19.01 |
|
|
|
Наименьшее общее кратное |
1 |
26.01 |
|
|
|
Зачет |
1 |
2.02 |
|
|
|
Зачет |
1 |
9.02 |
|
|
|
Уравнения в целых числах. |
1 |
16.02 |
|
|
|
Уравнения в целых числах. |
1 |
2.03 |
|
|
|
Уравнения в целых числах. |
1 |
9.03 |
|
|
|
Уравнения в целых числах. |
1 |
16.03 |
|
|
|
Уравнения в целых числах. |
1 |
23.03 |
|
|
|
Уравнения в целых числах. |
1 |
6.04 |
|
|
|
Уравнения в целых числах. |
1 |
13.04 |
|
|
|
Уравнения в целых числах. |
1 |
20.04 |
|
|
|
Зачет |
1 |
27.04 |
|
|
|
Зачет |
1 |
4.05 |
|
|
|
Конференция |
1 |
11.05 |
|
|
|
Конференция |
1 |
18.05 |
|
Требования к уровню усвоения учебного материала
В результате изучения программы элективного курса «Теория чисел» учащиеся получают возможность:
ЗНАТЬ:
-
различие между простыми и составными числами, а также способы образования фигурных, совершенными, дружественными числами;
-
способ нахождения наибольшего общего делителя и наименьшего общего кратного;
-
алгоритм Евклида;
-
приемы решения целочисленных уравнений.
УМЕТЬ:
-
определять НОД и НОК целых чисел, а также с помощью алгоритма Евклида.
-
применять основную теорему о разложении на множители
-
решать задачи на составление диофантовых уравнений.
-
находить способ решения задач, связанных с составлением диофантовых уравнений.
Методические рекомендации
При реализации программы целесообразно:
-
адаптировать учебный материал соответственно уровню подготовки контингента обучающихся. При этом доступность содержания не должна наносить ущерб его научности;
-
при обсуждении задач использовать эвристику - искусство поиска решения, в котором можно пользоваться какими угодно соображениями, нестрогими рассуждениями, в частности, геометрической интерпретацией;
-
предельно ориентировать содержание изученного материала на практическое применение;
-
уделять большое внимание процессу целеполагания;
-
обеспечить условия, необходимые для овладения способами самостоятельного взаимодействия с различными источниками информации настоящего времени;
-
использовать разнообразные методы контроля, итоговой формой контроля является сдача папки с решенными задачами по курсу (не менее 2 задач за занятие);
-
считать критерием эффективности изучения программы повышение интереса к предмету и дальнейшее обучение в 10 классе математического профиля.
Для практической части необходимо подбирать задачи из действующих учебников алгебры 8-9 классов, отмеченные (*), а также задачи повышенной трудности . Для развития мотивации к изучению курса следует подбирать (заимствовать) задачи из материалов вступительных экзаменов в ССУЗы и вузы , либо с некоторыми изменениями в них, такими, чтобы задачи непосредственно примыкали к задачам вступительных экзаменов и по содержанию, и по уровню трудности. С другой стороны, содержание вступительных экзаменов, уровень трудности предлагаемых задач достаточно неопределенны, и поэтому решение этих более сложных задач позволит построить процесс диагностики для создания 10 класса математического профиля и, кроме этого, создаст «запас прочности» на будущее.
На заключительном занятии элективного курса можно провести конференцию учащихся с подведением итогов решения задач и предоставлением каждым слушателем своей папки с решенными в ней задачами, заинтересовавшими их (за одно занятие в папку должно отбираться не менее двух задач). Составление папки с задачами способствует закреплению и систематизации знаний учащихся. В будущем она может пригодиться при подготовке к выпускным и вступительным экзаменам.
Список использованной литературы.
-
Айгнер М., Циглер Г. Доказательства из Книги. Лучшие доказательства со времен Евклида до наших дней. -М.: Мир, 2006.-265с.
-
Александров В.А., Горшенин С.М. Задачник - практикум по теории чисел- М.: Просвещение, 1972.-81с.
-
Алфутова Н.Б. Устинов А.В. Алгебра и теория чисел. Сборник задач для математических школ. - М.: МЦНМО, 2002.-264 с.
-
Бардушкин В.В., Кожухов М.Б., Прокофьев А.А., Фадеичева Т.П. Основы делимости в целых числах. Факультативный курс.- М.: МГИЭТ (ТУ),2003.-224с.
-
Виноградов И.М. Основы теории чисел. -Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003, 176с.
-
Галкин Е.В. Нестандартные задачи по математике. Задачи с целыми числами: Учебное пособие для учащихся 7-11 кл.- Челябинск: Взгляд. 2005.-271 с.
-
Горбачев Н.В. Сборник олимпиадных задач по математике - М.: МЦНМО, 2004.- 560с.
-
Гашков С.В. Современная элементарная алгебра в задачах и решениях.- М.: МЦНМО, 2006.-328 с.
-
Громов, А.И. Пособие-репетитор по математике. Подготовка к письменному экзамену [Текст]: Учебное пособие / А.И. Громов, В.М. Савчин. - Ростов н /Д: Феникс, 2001. - 480с.
-
Егоров А.А., Работ Ж.М.Олимпиады «Интеллектуальный марафон».Математика.- М.: Бюро Квантум, 2006.-128 с.
-
Ермаков, Д. Течения и «подводные камни» в море элективных курсов [Текст] / Д. Ермаков //Народное образование. - 2007. - №1. - 155-162.
-
Ермаков, Д.С. Создание элективных учебных курсов для профильного обучения [Текст] / Д.С. Ермаков, Г.Д. Петрова //Школьные технологии. - 2003. - №6. - С. 22-29.
-
.Канцель-Белов А.Я., Ковальджи А.К. Как решают нестандартные задачи/ Под ред. О.В. Бугаенко.- 4-е изд., стереотип.- М.: МЦНМО, 2008. 96с.
-
Концепция модернизации российского образования на период до 2010 г. [Текст] //Вестник образования. - 2002. - №6. - С.3-13.
-
Концепция профильного обучения на старшей ступени общего образования [Текст]//Стандарты и мониторинг в образовании. - 2002. - №3. - С.3-11.
-
Кудрявцев, Л.Д. О тенденциях и перспективах математического образования [Эл. ресурс]/ Л.Д. Кудрявцев, А.И. Кириллов, М.А. Бурковская, О.В. Зимина - www.AkademiaXXI.ru.
-
Мирошин В.В. Делимость натуральных чисел в задачах С6 из ЕГЭ. Математика в школе. Журнал. №3/ 2011, с.21.
-
Нестеренко Ю.В. Теория чисел: учебник для студентов высших учебных заведений.- М.: Издательский центр «Академия». 2008. -272с.
-
Об элективных курсах в системе профильного обучения на старшей ступени общего образования [Эл. ресурс]: Информационное письмо Департамента общего и дошкольного образования Минобразования России № 14-51-277/13 от 13.11.2003- www.profile-edu.ru
-
Оре.О . Приглашаем в теорию чисел.- М.: Едиторшал УРСС, 2003.-128с.
-
Петунин, О.В. Элективные курсы на этапе предпрофильной подготовки [Текст] /О.В. Петунин, Л.В. Трифонова // Школьные технологии. - 2006. - №1. - С.88-90.
-
Федяева Л.В. Элективные курсы по математике в системе профильного обучения [Эл. ресурс]/ Л.В. Федяева // Электронный научный журнал «Вестник Омского государственного педагогического университета». - 2007. - www.omsk.edu.
-
Черникова, Т.В. Методические рекомендации по разработке и оформлению программ элективных курсов [Текст]/ Т.В. Черникова // Профильная школа. - 2005. - №5. - С.11-16.
-
Элективные курсы в профильном обучении [Текст] /Министерство образования РФ - Национальный фонд подготовки кадров. - М.: Вита-Пресс, 2004. - 144c.
Разработка занятий элективного курса «Теория чисел»
Занятия 1-3. Теория чисел. Нумерология.
Цель: Открыть тайны мира чисел. Познакомить с обозначением чисел у разных народов в прошлом и числами великанами, показать их жизненную необходимость
Закрепление знаний по теме «Теория чисел. Нумерология»; развитие умения решать нестандартные задачи.
Ход занятия:
1. Организационный момент. Введение в элективный курс «Теория чисел», сообщение целей и задач данного курса, требований к учащимся, форм и методов работы, системы контроля уровня достижений учащихся и критериев оценки, ожидаемого результата по окончании изучения курса.
2. Обзорная лекция по теме Теория чисел. Нумерология.
Теория чисел - это ветвь математики, имеющая дело с целыми положительными числами 1,2,3,…, которые также называют натуральными.
Число-это основное понятие современной
математики. Но что такое число? Если мы говорим, что![]() или что (-1)*(-1)=1, то какой смысл
выкладывается в эти утверждения?
или что (-1)*(-1)=1, то какой смысл
выкладывается в эти утверждения?
Греки в древнее время в основу созданной или математики положили геометрические концепции точки и прямой; руководящим принципом современной математики стало сведение, в конечном счете всех утверждений к утверждениям, касающимся натуральных чисел 1,2,3. …. «Бог создал натуральные числа, все прочее дело рук человека». Этими словами Леопольд Кронекер (1823-1891) определил тот прочный фундамент, на котором может быть построено здание математики.
Изучение натуральных чисел было начато в Древней Греции. Евклид и Эратосфен открыли свойства делимости чисел, доказали бесконечность множества простых чисел и нашли способы их построения. Задачи, связанные с решением неопределенных уравнений в целых числах, были предметом исследований Диофанта, а также ученых Древней Индии и древнего Китая, стран Средней Азии.[28]
История возникновение чисел разных народов.
Изучая явление природы и окружающей жизни, люди везде находили предметы для счета. Число возникло с появлением у человека потребности практической деятельности. Числовые представления (как и наша речь) неразрывно связаны с существованием самого человека, так как на всех ступенях своей истории он был связан с процессом счета окружающих предметов и проведением каких-то измерений. «Число - это закон и связь мира, сила, царящая над богами и смертными». «Все есть число». Вот такие положения проповедовал древнегреческий математик Пифагор. Наибольшие числа натурального ряда, которые постигали в результате счета, породили у человека много числовых суеверий и мистических представлений, были для него таинственными, наделялись сверх естественными свойствами и считались священными. Запись чисел при помощи цифр возникла не сразу. В течении многих веков люди писали все числа словами. Это занимало много времени и места, было не наглядно и затрудняло действия. Постепенно слова стали сокращать или писать только начальными буквы слов, выделяя их из среды других букв особыми знаками. Некоторые народы от записи слова перешли к записи специально придуманными знаками. Знаки эти у разных народов были различными, да и у одного народа встречались неодинаковые знаки для обозначения одних и тех же цифр. Возникали недоразумения, люди перестали понимать друг друга. Потребовались многие сотни лет, чтобы выработать единые знаки и систему записи чисел. Египтяне имели нумерацию с десятичной основой. Рассмотрим цифры некоторых народов:
1. Цифры, которыми пользовались египтяне около 4000 лет назад.

2. Вавилонские цифры. Они тоже употреблялись около 4000 лет назад:
![]()
У вавилонян - шести десятеричная система счисления.
3. У китайцев в ходу было несколько систем цифр. Вот цифры ученых трактатов:
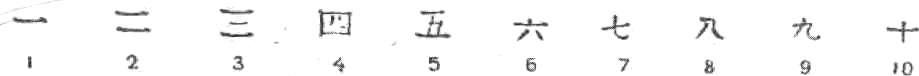
А эти цифры коммерческие, употреблявшиеся купцами и торговцами:
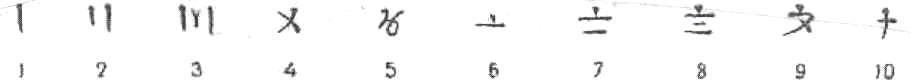
4. В древней Греции первые 9 букв алфавита с черточками над ними
обозначали числа от 1 до 9. следующие 9 букв обозначали десятки,
последние - сотни:
Таким образом, число 23 греки писали,
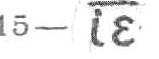

Для обозначения тысяч применялись те же буквы, что и для первого десятка, но они отделялись от сотен, запятой.
5. Г В IX в. славянские просветители - монахи братья Кирилл (умер в 869 г.) и Мефодий (умер в885г.) - по образцу и подобию греческой нумерации составили церковнославянскую нумерацию для Южной Руси.
С годами вместе с церковными книгами эта нумерация проникла в Центральную и Северную Русь и держалась около 700 лет. Церковнославянская нумерация - точная копия греческой нумерации. Каждая буква независимо от ее положения обозначала одно и то же число.
Вот таблица славяно-греческих числовых знаков:

Образцы записи чисел в старинной русской нумераций;
ЧИСЛО 85 по-славянски записывалось:

Число 128 по-славянски записывалось:
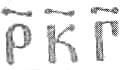
Чтобы указать, что эти буквы следует считать числами, над каждой из них ставили особый знак:

(титло).
Для обозначения тысяч, перед числом тысяч ставили значок.
Для обозначения десятков ,тысяч (славяне называли это число тьмою),
букву ставкой в кружок.
Нуль не обозначался никак и не писался вообще. Для обозначения
сотен тысяч букву брали в кружок из точек» .
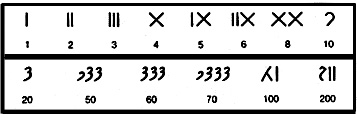
2 Римская пятеричная

Это, наверное, самая известная система, после «арабской», она возникла более двух с половиной тысяч лет назад в Древнем Риме.
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Например, XI = 11, XII = 12, XIII = 13, но следующее число уже особенное, так как такое число «XIIII» писать неудобно, римляне придумали сокращения, они стали писать так XIV = 14, т.е. 10+5-1 = 14. Т.е. если цифра с меньшим значением записывалась перед цифрой с большим значением, то происходило ее вычитание. Так же записывалось число 9 = IX. И кроме этого нельзя было писать четыре одинаковые цифры подряд, например, «XXXX» = XL (50-10) = 40.
О происхождении римских цифр достоверных сведений нет. В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян ни каких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (скорее всего этрусков). Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы - до XVI века.
В Санкт- Петербурге стоит памятник Петру I. На гранитном постаменте памятника есть римское число: MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 год. Это год открытия памятника.
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д.
3.3 Древнегреческая аттическая пятеричная
В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции - Аттики со столицей Афины.
В этой системе числа 1, 2, 3, 4 изображались соответствующим
количеством вертикальных полосок: ![]() ,
,![]() ,
,![]() ,
,![]() . Число 5 записывалось знаком
. Число 5 записывалось знаком
![]() (древнее
начертание буквы "Пи", с которой начиналось слово "пять" -
"пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
(древнее
начертание буквы "Пи", с которой начиналось слово "пять" -
"пенте"). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:
![]()
Число 10 обозначалось ![]() - заглавной "Дельта" от слова
"дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X,
M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5
и 100, 5 и 1 000, а именно:
- заглавной "Дельта" от слова
"дека" - "десять". Числа 100, 1 000 и 10 000 обозначались H, X,
M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5
и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:
![]()
3.4 Древнегреческая ионийская десятеричная алфавитная
Примерно в третьем веке до нашей эры аттическая система счисления в Греции была вытеснена другой, так называемой "Ионийской" системой (она возникла в Милеете - греческая малоазиатская колония Ионии). В ней числа 1 - 9 обозначаются первыми буквами древнегреческого алфавита:
![]()
числа 10, 20, … 90 изображались следующими девятью буквами:
![]()
числа 100, 200, … 900 последними девятью буквами:
![]()
Для обозначения тысяч и десятков тысяч пользовались теми же цифрами, но только с добавлением особого значка '. Любая буква с этим значком сразу же становилась в тысячу раз больше.
Для отличия цифр и букв писали черточки над цифрами.
![]()
Древние евреи, арабы и многие другие народы Ближнего Востока имели такие же системы счисления.
При ее помощи можно было просто записать числа до ста миллионов (100 000 000). Эта система по быстроте счета мало отличается от «арабской». И хоть она не позиционная, но в ней есть мультипликативность.
3.5 Славянская глаголическая десятеричная
Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.
![]()
![]()
![]() = 800+60+3 = 863
= 800+60+3 = 863
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, или точки.
3.6 Славянская кириллическая десятеричная алфавитная
Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:
![]()
Читаем дословно "четырнадцать" - "четыре и десять". Как слышим, так и пишем: не 10+4, а 4+10, - четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.
Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:
![]() =
800+60+3
=
800+60+3
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
Тысяча
1000

Тьма
10 000

Легион
100 000

Леодр
1 000000

Ворон
10 000000

Колода
100 000000
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
7 Древнеиндийские системы счисления
Употребляемая нами система нумерации и цифры зародились в Индии не позже V в. н. э. Главное преимущество индийской системы заключается в том, что значение каждой цифры определяется ее местом в числе. Нам это кажется очень простым, но додуматься до этого было очень трудно. Это было величайшим открытием в мировой науке древних.
Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.
Наряду с этой системой существовала в Индии еще одна система счисления Брахме.
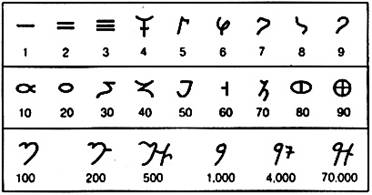
Числа Брахме записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр Брахме, было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр Брахме в дальнейшем была использована при создании в Индии позиционной десятичной системы.
В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.
8.Древнекитайская десятеричная
Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.




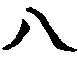 - 5 * 100+4*
10+8 = 548
- 5 * 100+4*
10+8 = 548
Эта мультипликативная запись, так как в ней используется умножение. Она десятичная, в ней есть знак нуля, кроме этого она позиционная. Т.е. она почти соответствует «арабской» системе счисления.
9. Двадцатеричная система счисления индейцев Майя или долгий счет
Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).
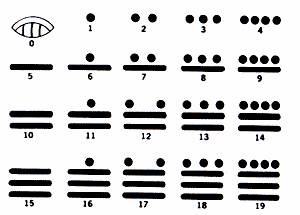
Число 20 изображалось из двух цифр, ноль и один наверху
![]() и называлось уиналу. Записывались числа столбиком, внизу
располагались наименьшие разряды, вверху наибольшие, в
результате получалась «этажерка» с полками. Если число ноль
появлялось без единицы наверху, то это обозначало, что
единиц данного разряда нет. Но, если хоть одна единица была
в этом разряде, то знак нуля исчезал, например, число 21,
это будет
и называлось уиналу. Записывались числа столбиком, внизу
располагались наименьшие разряды, вверху наибольшие, в
результате получалась «этажерка» с полками. Если число ноль
появлялось без единицы наверху, то это обозначало, что
единиц данного разряда нет. Но, если хоть одна единица была
в этом разряде, то знак нуля исчезал, например, число 21,
это будет ![]() . Так же в нашей системе
счисления: 10 - с нулем, 11 - без него. Вот несколько
примеров чисел:
. Так же в нашей системе
счисления: 10 - с нулем, 11 - без него. Вот несколько
примеров чисел:

В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу 359 только одну единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: 360 является начальным числом третьего порядка и его место уже не на второй, а на третьей полке.
Но тогда выходит, что начальное число третьего порядка больше начального числа второго не в двадцать раз (20x20=400, а не 360!), а только в восемнадцать! Значит, принцип двадцатеричности нарушен! Все верно. Это и есть исключение.
Дело в том, что у индейцев Майя 20 дней-кинов образовывали месяц или уинал. 18 месяцев-уиналов образовывали год или туну (360 дней в году) и так далее:
К'ин = 1 день.
Виналь = 20 к'ин = 20 дней.
Тун = 18 виналь = 360 дней = около 1 года.
К'атун = 20 тун = 7200 дней = около 20 лет.
Бак'тун = 20 к'атун = 144000 дней = около 400
лет.
Пиктун = 20 бак'тун = 2880000 дней = около 8000
лет.
Калабтун = 20 пиктун = 57 600 000 дней = около
160000 лет.
К'инчильтун = 20 калабтун = 1152000000 дней = около
3200000 лет.
Алавтун = 20 к'инчильтун = 23040000000 дней = около
64000000 лет.

Это довольно сложная система счисления, в основном использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была аддитивной, похожей на египетскую и применялась в повседневной жизни.
История «арабских» чисел.
История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно как они произошли. Вот один из вариантов этого истории этого происхождения. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа.
Как мы уже знаем, в вавилонской системе счисления присутствует знак для обозначения пропущенных разрядов. Примерно во II веке до н.э. с астрономическими наблюдениями вавилонян познакомились греческие астрономы (например, Клавдий Птолемей). Они переняли их позиционную систему счисления, но целые числа они записывали не с помощью клиньев, а в своей алфавитной нумерации, а дроби в вавилонской шестидесятеричной системой счисления. Но для обозначения нулевого значения разряда греческие астрономы стали использовать символ "0" (первая буква греческого слова Ouden - ничто).
Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Это и был завершающий шаг в создании позиционной десятичной системы счисления.
Блестящая работа индийских математиков была воспринята арабскими математиками и Аль-Хорезми в IX веке написал книгу "Индийское искусство счета", в которой описывает десятичную позиционную систему счисления. Простые и удобные правила сложения и вычитания сколь угодно больших чисел, записанных в позиционной системе, сделали ее особенно популярной в среде европейских купцов.
В XII в. Хуан из Севильи перевел на латынь книгу "Индийское искусство счета", и индийская система счета широко распространилась по всей Европе. А так как труд Аль-Хорезми был написан арабском языке, то за индийской нумерацией в Европе закрепилось неправильное название - "арабская". Но сами арабы именуют цифры индийскими, а арифметику, основанную на десятичной системе - индийским счетом.
 Форма «арабских» цифр со
временем сильно изменялась. Та форма, в которой мы их
пишем, установилась в XVI веке.
Форма «арабских» цифр со
временем сильно изменялась. Та форма, в которой мы их
пишем, установилась в XVI веке.

Самое трудное было придумать нуль. Его придумали на много веков позже, чем другие цифры. Первая, точно датированная запись, в которой встречается знак нуля, относится к 876 г. Но это не значит, что до этого знак нуля не употреблялся. Он был открыт, вероятно, около 500 г, н.э. может быть, даже и раньше. До изобретения нуля индийцы пользовались своей системой нумерации без нуля. Вместо него ставили черточки, писали словами и т. д. В VIII в, арабы переняли индийскую нумерацию и передали ее в Европу. На Руси индийские цифры стали известны в начале XVII в/ Христианская церковь- приняла новые цифры враждебно. Причина заключалась в том, что новью цифры и система записи чисел были просты и доступны всякому. Люди потянулись к знаниям, а этого-то как раз и не хотели попы задачей, которых было тормозить распространение грамоты и математических знаний. Была и еще одна причина враждебного отношения христианской церкви к новым цифрам. В те годы шла яростная борьба между византийской и римско-католической церквами за влияние на Руси. У католиков в употреблении были новые цифры. В борьбе за господство на Руси византийская церковь оказывала сопротивление всему, что в какой-то степени было связано с католицизмом. Индийская нумерация и десятичная система записи чисел были объявлены безбожными и колдовскими, книги, в которых встречались новые цифры, запрещалось не только читать, а даже держать у себя дома. Тех, кто нарушал это, жестоко наказывали. Так, например, в 1676 г. боярину Морозову было предъявлено обвинение в колдовстве и чернокнижии только па-тому, что у него дома была найдена медицинская книга, в которой "... писаны многие статьи цифирью». Боярин поплатился за свое «вольнодумство».
Теперь индийские цифры и десятичная система нумерации применяются во всем мире, и мы почти не задумываемся над тем» как долог и как труден был путь ее развития. Числа великаны
Наибольшие числа натурального ряда, которые постигали в результате счета, породили у человека много числовых суеверий и мистических Наибольшие числа натурального ряда, которые постигали в результате счета, породили у человека много числовых суеверий и мистических представлений, были для него таинственными, наделялись сверх естественными свойствами и считались священными.
Посмотрим, какие есть числа великаны.
На примере сказки «Легенде о шахматах».
Задача: на первую клетку шахматной доски положили одно зерно, на вторую -два зерна, на треть четыре итак до 64клетки, постоянно удваивая число зерен предыдущей клетки.
Вот это число 18446744073709551615. Если10 зерен весят один грамм, то это 184 миллиарда467 миллионов440 тысяч 737 тонн 95 килограммов и 516 граммов пшеницы. Если на всей земле за год выращивают 2 миллиарда тонн, то, это зерно надо выращивать 92 года.
Как записать это число- .S =18,5* !0
3. Задание для самостоятельной работы:
Задача: Сделка. Каждый день получаешь по 100000рублей, а отдавать в первый день 1 копейку. Во «день -4 копейки и так целый месяц.
Итог: получил 3 миллиона, отдал 10 миллионов.
Задача : Как велик миллиард? За сколько времени вы смогли бы сосчитать до миллиарда?
Итог: За 1 минуту можно сосчитать до 125. 1000000000 :125 =8000000 мин = 133333час =5555суток =15 лет, если считать по 8 час в сутки, то пришлось бы считать 45 лет.
Задача: Посчитайте сколько времени лететь до Солнца?
Итог: До Солнце около 150000000км, а космическая ракета пролетает за час 40000км !50000000:40000= 4000час=166дней.
Задача: Быстрое размножение. Спелая маковая головка полна крошечных зернышек: из каждого может вырасти целое растение. Сколько же получится маков, если зернышки все до единого прорастут?
Итог: Чтобы узнать это, надо сосчитать зернышки в целой головке. Скучное занятие, но результат так интересен, что стоит запастись терпением и довести счет до конца. Оказывается, одна головка мака содержит (круглым числом) 3000 зернышек. Что отсюда следует? То, что будь вокруг нашего макового растения достаточная площадь подходящей земли, каждое упавшее зернышко дало бы росток, и будущим летом на этом месте выросло бы уже 3000 маков. Целое маковое поле от одной головки! Посмотрим же, что будет дальше. Каждое из 3000 растений принесет не менее одной головки (чаще же несколько), содержащей 3000 зерен. Проросши, семена каждой головки дадут 3000 новых растений, и, следовательно, на второй год у нас будет уже не менее 3000 х 3000 = 9 000000 растений. Легко рассчитать, что на третий год число потомков нашего единственного мака будет уже достигать.9000000 х 3000 = 27000000000.А на четвертый год.27000000000 х 3000 = 81000000000000. Й на пятом году макам станет тесно на земном шаре, потому что число растений сделается равным.81000000000000 х 3000 = 243 000000000000000. Поверхность же всей суши, т. е. всех материков и островов земного шара, составляет только 135 миллионов квадратных километров, - 135000000000000 кв. м. - примерно в 2000 раз менее чем выросло бы экземпляров мака. Вы видите, что если бы все зернышки мака прорастали, потомство одного растения могло бы уже в пять лет покрыть сплошь всю сушу земного шара густой зарослью по две тысячи растений на каждом квадратном метре. Вот какой числовой великан скрывается в крошечном маковом зернышке.
4. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 4.Задача Пифагора.
Цель: Познакомить с задачей Пифагора.
Ход занятия:
1.Обзорная лекция.
Примером ранней теории чисел может служить задача Пифагора. Как мы знаем, в прямоугольном треугольнике длины сторон удовлетворяют соотношению Пифагора z2=x2+y2, где z- длина гипотенузы. Это дает возможность в прямоугольном треугольнике вычислить длину одной стороны, если известны две другие. Между прочим, то, что эту теорему назвали в честь греческого философа Пифагора, не совсем справедливо: она была известна вавилонянам почти за 2000 лет до Пифагора.
Иногда все длины сторон x,y,z выражаются целыми числами. Простейший случай, x=3, y=4, z=5, был найден на вавилонских глиняных табличках. Этому случаю можно дать следующие истолкование. Предположим, что у нас есть веревочное кольцо с узелками или метками, расположенными на равных расстояниях и делящими кольцо на 12 частей. Тогда, если мы растянем кольцо на трех колышках, вбитых на поле, так, чтобы получился треугольник со сторонами 3 и 4, то третья сторона будет иметь длину 5, а противоположный ей угол будет прямым. Часто можно прочесть в книгах по истории математики, что именно этот метод построения прямого угла использовался египетскими землемерами или «натягивателями веревки» при размежевании полей по окончании разлива Нила. Однако вполне возможно, что это один из мифов, в которых так много в истории науки; у нас нет документов, подтверждающих это предположение.
Существует много других целочисленных решений уравнения Пифагора, например,
X=5, y=12, z=13,
X=7, y=24, z=25,
X=8, y=15, z=17.
Далее мы покажем, как можно получить все такие решения. Способ находить их был известен древним грекам, а возможно, и вавилонянам.
Если даны два целых числа, х и у, то всегда можно найти соответствующее число z, удовлетворяющее уравнению, но вполне возможно, что z будет иррациональным числом. Если же потребовать, что все три числа были целыми, то тогда возможности существенно ограничиваются. Греческим математик Диофант (время его жизни точно неизвестно, приблизительно 200г. нашей эры) написал книгу Arithmetica («Арифметика»), в которой рассматриваются подобные задачи. С этого времени задача нахождения целочисленных или рациональных решений уравнений называется задачей Диофанта, а диофантов анализ - важная часть современной теории чисел. [28]
3. Задания для самостоятельной работы:
1.Попытайтесь найти другое решение уравнения Пифагора в целых числах.
2.Попытайтесь найти решения уравнения Пифагора, в которых гипотенуза на единицу больше, чем больший из двух катетов.
4. Подведение итогов.
- Какова была тема занятия? Что нового узнали на занятии?
- Достигли ли цели, поставленной в начале занятия?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 5. Фигурные числа
Цель: Познакомить детей с фигурными числами.
Ход занятия.
1.Обзорная лекция.
В теории чисел мы часто встречаемся с квадратами, т.е. такими числами, как 32=9, 72=49, 102=100. и аналогично с кубами, т.е. такими числами, как 23=8,33=27,53=125.
Этот геометрический образ рассматриваемой операции с числами является частью богатого наследства, оставленного древнегреческими мыслителями. Греки предпочитали думать о числах, как о геометрических величинах: произведение c=a*b рассматривалась как площадь с прямоугольника со сторонами a и b. Также можно было рассматривать a*b как число точек в прямоугольной таблице с а почками на одной стороне и b точками на другой. Например, 20=4*5 есть число точек в прямоугольной таблице (рис. 1).
. . . . .
. . . . .
. . . . .
. . . . .
рис.1
Любое целое число, которое является произведением двух целых чисел, можно было бы назвать прямоугольным числом. Когда две стороны прямоугольника имеют одну и ту же длину, то такое число является квадратным числом, и квадратом. Некоторые числа нельзя представить в виде прямоугольных чисел иначе, как тривиальным способом - в виде цепочки точек, лежащих в одном ряду. Например, пять может быть представлено как прямоугольное число лишь единственным способом, взяв одну сторону равной единице, а другую пяти (рис.2).
. . . . .
Рис.2
Такие числа греки называли простыми. Точка, взятая в одном экземпляре, не рассматривалась как число. Число 1 являлось тем кирпичом, из которого строились остальные числа. Таким образом, 1 не была для них и ни считается сейчас простым числом.
Можно было бы рассматривать точки, равномерно заполняющие не только прямоугольники и квадраты, но и другие геометрические фигуры. Последовательные треугольные числа изображены на рис.3.
В общем случае n-е треугольное число задается формулой
![]() , n=1,2,3,…
, n=1,2,3,…
У этих чисел масса интересных свойств: например, сумма двух последовательных треугольных чисел является квадратом
1+3=4. 3+6=9, 6+10=16 и т.д.
1 3 5 7 8 11
Рис.5
Глядя на него, легко найти несколько первых пятиугольных чисел, 1,5, 12, 22, 35.
Можно показать, что n-е пятиугольное число выражается формулой
![]() .
.
Шестиугольные числа. И вообще k-угольные числа, аналогично определяются с помощью правильного k-угольника.
Проводя анализ такого геометрического представления чисел, можно получить несколько простых соотношений. Остановимся лишь на одном примере. Уже давно было известно, что складывая последовательно нечетные числа, мы все время будем получать квадраты, например,
1+3=4, 1+3+5=9, 1+3+5+7=16 и т.д.
Чтобы доказать это соотношение, достаточно, лишь взглянуть на рис.5, на котором изображены последовательно вложенные квадраты.
Пифагорейцы рассматривали и пространственные фигурные числа, например, кубы 1, 8, 27 и так далее, а также пирамидальные числа, равные сумме треугольных чисел. [28]
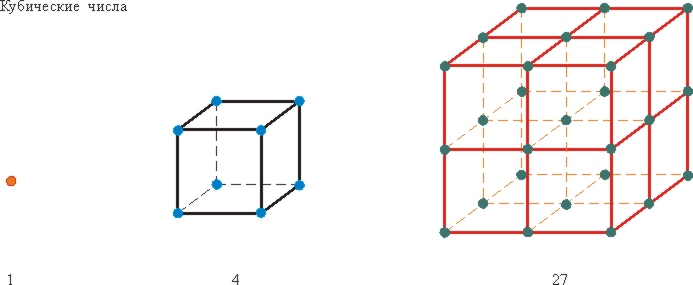
Рис. 6. Класс кубических чисел
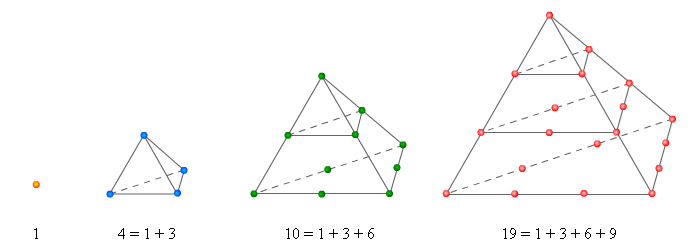
Рис. 7. Класс пирамидальных чисел.
3.Задания для работы в классе.
4. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Учащиеся в паре оценивают работу друг друга по пятибалльной шкале. Также учитель ставит по одному баллу наиболее активным учащимся.
Занятие 6-7. Магические квадраты.
Цель: Познакомить учащихся с магическими квадратами и способами их образования.
Ход урока:
1.Обзорная лекция.
МАГИЧЕСКИЙ КВАДРАТ, квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Магический квадрат - древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 1,а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату, изображенному на рис. 1,б. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 веке магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 веке византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 2), изображенный на его знаменитой гравюре Меланхолия 1. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
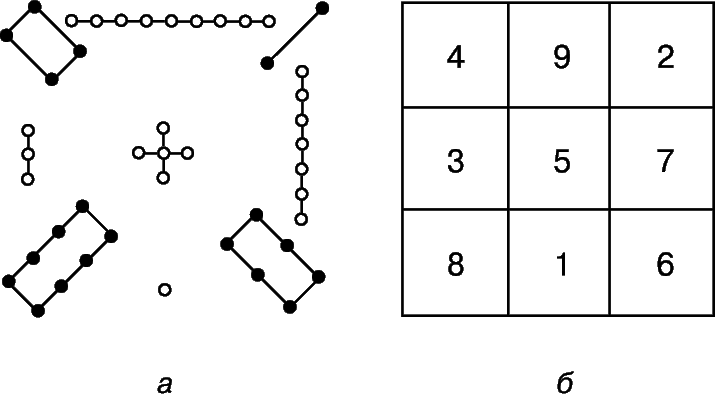
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n2 клеток и называется квадратом n-го порядка. В большинстве магических квадратов используются первые n последовательных натуральных чисел. Сумма S чисел, стоящих в каждой строке, каждом столбце и на любой диагонали, называется постоянной квадрата и равна S = n(n2 + 1)/2. Доказано, что n 3. Для квадрата 3-го порядка S = 15, 4-го порядка - S = 34, 5-го порядка - S = 65.
Две диагонали, проходящие через центр квадрата, называются главными диагоналями. Ломаной называется диагональ, которая, дойдя до края квадрата, продолжается параллельно первому отрезку от противоположного края (такую диагональ образуют заштрихованные клетки на рис. 3). Клетки, симметричные относительно центра квадрата, называются кососимметричными. Таковы, например, клетки a и b на рис. 3.
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы, некоторые из которых мы рассмотрим ниже.
Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А .де ла Лубера. Рассмотрим этот метод на примере квадрата 5-го порядка (рис. 4). Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата (как в случае числа 1), продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца. Дойдя до правого края квадрата (число 3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (число 5) или угла (число 15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
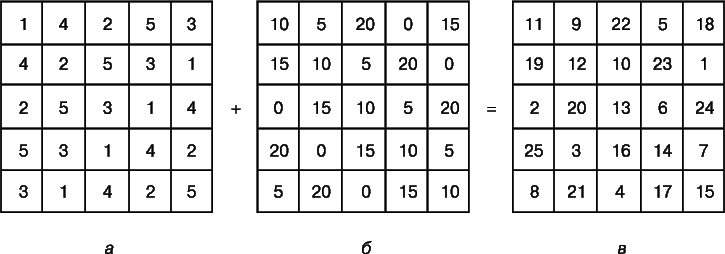
Метод Ф.де ла Ира (1640-1718) основан на двух первоначальных квадратах. На рис. 5 показано, как с помощью этого метода строится квадрат 5-го порядка. В клетку первого квадрата вписываются числа от 1 до 5 так, что число 3 повторяется в клетках главной диагонали, идущей вправо вверх, и ни одно число не встречается дважды в одной строке или в одном столбце. То же самое мы проделываем с числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь повторяется в клетках главной диагонали, идущей сверху вниз (рис. 5,б). Поклеточная сумма этих двух квадратов (рис. 5,в) образует магический квадрат. Этот метод используется и при построении квадратов четного порядка.
МАГИЧЕСКИЙ КВАДРАТ
Е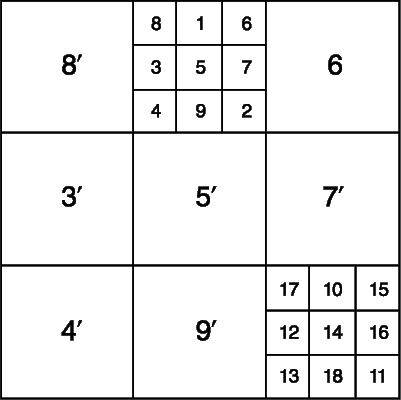 сли известен способ
построения квадратов порядка m и порядка
n, то можно построить квадрат порядка
mn. Суть этого способа показана на
рис. 6. Здесь m = 3 и n = 3. Более
крупный квадрат 3-го порядка (с числами, помеченными
штрихами) строится методом де ла Лубера. В клетку с
числом 1 (центральную клетку верхнего ряда)
вписывается квадрат 3-го порядка из чисел от 1 до 9,
также построенный методом де ла Лубера. В клетку с
числом 2 (правую в нижней строке) вписывается
квадрат 3-го порядка с числами от 10 до 18; в клетку
с числом 3 - квадрат из чисел от 19 до 27 и т.д. В
результате мы получим квадрат 9-го порядка. Такие
квадраты называются составными.[28].
сли известен способ
построения квадратов порядка m и порядка
n, то можно построить квадрат порядка
mn. Суть этого способа показана на
рис. 6. Здесь m = 3 и n = 3. Более
крупный квадрат 3-го порядка (с числами, помеченными
штрихами) строится методом де ла Лубера. В клетку с
числом 1 (центральную клетку верхнего ряда)
вписывается квадрат 3-го порядка из чисел от 1 до 9,
также построенный методом де ла Лубера. В клетку с
числом 2 (правую в нижней строке) вписывается
квадрат 3-го порядка с числами от 10 до 18; в клетку
с числом 3 - квадрат из чисел от 19 до 27 и т.д. В
результате мы получим квадрат 9-го порядка. Такие
квадраты называются составными.[28].
3. Закрепление изученного материала.
4. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 8 .Решето Эратосфена.
Цель: Познакомить учащихся с таблицей простых чисел (решетом Эратосфена).
Ход урока:
1.Обзорная лекция.
Существует таблицы простых чисел, простирающиеся до очень больших чисел. Как можно было подступиться к составлению такой таблицы? Эта задача была решена (около 200г. до н.э.) Эратосфеном, математиком из Александрии. Его схема состоит в следующем: напишем последовательность всех целых чисел от 1 до числа, которым хотим закончить таблицу:
1 2 3 4 5 6 7 8 9 1 0 11 12 13 14 15
2 2 2 3 2 2 2 3
Начнем с простого числа 2. Будем выбрасывать каждое второе число, начиная со 2 ( кроме самого числа 2), т.е четные числа 4, 6, 8, 10 и т.д., подчеркивая каждое из них. После этой операции первым неподчеркнутым числом будет число 3. Оно простое, так как не делиться на 2. Оставив число неподчеркнутым, будем подчеркивать каждое третье число после него, т.е. числа 6, 9. 12, 15, …;некоторые из них уже были подчеркнуты, поскольку они являются четными. На следующем шаге первым неподчеркнутым числом окажется число 5; оно простое, так как не делится ни на 2, ни на 3. Оставим число 5 неподчеркнутым. Но подчеркнем каждое пятое число после него, т.е. числа 10, 15, 20, 25, …; как и раньше, часть из них уже оказалась подчеркнутой. Теперь наименьшим неподчеркнутым числом окажется число 7. оно простое, так как не делится ни на одно из меньших его простых чисел 2,3, 5. Повторяя этот процесс получим последовательность неподчеркнутых чисел; все они (кроме числа 1) являются простыми.
Так как во времена Эратосфена писали на восковых табличках и не вычеркивали, а "выкалывали" цифры, то табличка после описанного процесса напоминала решето. Поэтому метод Эратосфена для нахождения простых чисел получил название «решето Эратосфена»

Многие важные результаты в современной теории чисел были получены методом решета. Приведем результат, известный еще Евклиду:
Существует бесконечное число простых чисел:
Доказательство. Предположим, что существует k простых чисел:
2, 3, 5, …, pk.
Тогда в решете не оказалось бы неподчеркнутых чисел, больших чем pk.Но это невозможно, так как произведение этих простых чисел
p= 2*3*5… pk
будет отсеиваться k раз, по разу для каждого простого числа, поэтому следующее число p+1 не может быть подчеркнуто ни для одного из них. [28]
2.Закрепление изученного материала.
-
Составьте таблицы простых чисел для каждой из сотен: 1-100, 101-200,…., 901-1000 .
-
Попытайтесь определить количество простых чисел в диапазоне 10001-10100.[28]
3.Подведение итогов урока:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 9-13. Простые и составные числа.
Цель:
Познакомить учащихся с простыми и составными числами и способом образования составных чисел.
Ход урока:
1.Обзорная лекция.
Должно быть, одним из первых свойств чисел, открытых человеком, было то, что некоторые из них могут быть разложены на два или более множителя, например,
6=2*3, 9= 3*3, 30=2*15=3*10,
в то время как другие например,
3 , 7, 13, 37,
не могут быть разложены на множители подобным образом. Число c=a*b является произведением двух чисел a и b, то называем a и b множителями или делителями числа с. Каждое число имеет тривиальное разложение на множители
c=1*c=c*1
Соответственно называем числа 1 и с тривиальными делителями числа с.
Любое число c>1, у которого существует нетривиальное разложение на множители, называется составным. Если число с имеет только тривиальное разложение на множители, то оно называется простым. Среди первых 100 чисел простыми являются следующие 25 чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Все остальные числа, кроме 1, являются составными. Мы можем сформулировать следующее утверждение:
Теорема 1. Любое целое число c>1 является либо простым, либо имеет простой множитель.
Доказательство. Если с не является простым числом, то у него есть наименьший нетривиальный множитель р. Тогда р - простое число, так как если бы р - было составным, то число с имело бы еще меньший множитель.
Теперь мы подошли к нашей первой важной задаче в теории чисел: как определить, является ли произвольное число простым или нет, и в случае, если оно составное, то как найти какой-либо его нетривиальный делитель?
Первое, что может прийти в голову, - это
попытаться разделить данное число с на все числа,
меньшие его. Но надо полагать, что этот способ мало
удовлетворителен. Согласно теореме 1идостаточно
делить на все простые числа, меньшие с. Но мы можем
значительно упростить задачу, заметив. Что при
разложении на множители c=a*b оба множителя a и b не
могут быть больше, чем ![]() , так как в противном
случае получили бы a*b>
, так как в противном
случае получили бы a*b>![]() *
*![]() =с, что невозможно.
Таким образом, чтобы узнать, имеет ли число с
делитель, достаточно проверить, делится ли число с на
простые числа не превосходящие
=с, что невозможно.
Таким образом, чтобы узнать, имеет ли число с
делитель, достаточно проверить, делится ли число с на
простые числа не превосходящие ![]() .
.
Пример 1. Если с=91, то ![]() =9,…; проверив простые
числа 2,3, 5, 7, находим, что 91=7*13.
=9,…; проверив простые
числа 2,3, 5, 7, находим, что 91=7*13.
Пример 2. Если с=1973, то находим, что ![]() =44,… Так как ни одно
из простых чисел до 43 не делит с, по число является
простым.
=44,… Так как ни одно
из простых чисел до 43 не делит с, по число является
простым.
Очевидно, что для больших чисел этот метод может быть трудоемким. Как и при многих других вычислениях в теории чисел, можно использовать современные методы, т.е применение калькулятора и компьютера.
Другим очень простым методом является применение таблиц простых чисел. т.е. использование простых чисел уже найденными другими. За последние 200 лет было составлено и издано много таблиц простых чисел. Наиболее обширной является таблица Д.Х. Лемера, содержащая все простые числа до 10000000. Приведенная ниже таблица содержит все простые числа до 1000.
Разложение натуральных чисел на множители (каноническое разложение натуральных чисел)
Теорема 2. Любое натуральное число, отличное от 1, можно представить в виде произведения множителей, являющихся простыми числами, причем единственным образом.
Иногда эту теорему формулируют так: любое натуральное число, отличное от 1, можно единственным образом разложить на простые множители.
Например,
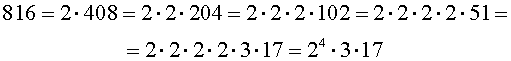
Равенство
![]()
и есть единственное разложение числа 816 на простые множители. Простыми множителями в данном примере являются числа 2, 3 и 17.
</ Бесконечность множества простых чисел
Теорема 3. Множество простых чисел бесконечно.
Доказательство. Будем доказывать эту теорему от противного, предположив, что множество простых чисел конечно.
Тогда рассмотрим число, равное произведению всех простых чисел плюс 1. Это число не делится ни на одно из простых чисел, поэтому его разложение на простые множители с одной стороны должно существовать, а с другой стороны не может содержать ни одного из множителей, являющихся простым числом.
Полученное противоречие доказывает, множество простых чисел должно быть бесконечным.
Таблица 1.
Простые числа среди первой тысячи чисел.
Задания.
-
Какие из следующих чисел являются простыми: а) год вашего рождения; б) текущий год, в) номер вашего дома.
-
Найдите простое число, следующее за простым число 1973.
-
Задача. Доказать, что полусумма двух последовательных простых чисел больших 2 является составным числом.
Решение. Поскольку все простые числа большие 2 являются нечетным числом, то их сумма будет четным числом, а полусумма - натуральным числом. [28]
-
а) Найти каноническое разложение числа 82798848.
Решение: 28*35*113
б) Найти каноническое разложение числа 81057226635000.
Решение: 23*33*54*73*112*17*23*37. [36]
5. К двузначному числу приписали такое же число. Может им полученное четырехзначное число быть простым.
6. Натуральные числа a и b таковы, что 31a=54 b. Докажите, что число a+b составное.
7. Натуральные числа a и b удовлетворяют условию 15а=32в. Может ли число a-b быть простым?
8. Какие остатки при делении на 6 может иметь простое число, большее, чем 3?
9.Докажите, что если a>1, то число a4+4 составное.
10.Докажите, что если произведение ab делится на простое число P, то хотя бы одно из числа а, в делится на P.
11.Известно, что числа p, p+10; p+14 простое. Чему равно p? [8]
4. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
-
Домашнее задание:
1.Определите, являются ли число 353 простым.
2. Какие из чисел, заключенных между 2320 и 2350 являются простыми?
3. Каким из чисел, заключенных между 40322 и 40330, являются простыми?
4. Какие из чисел, заключенных между 3628802 и 3628810, являются простыми? [36]
Занятие 12. Основная теорема о разложении на множители.
Цель: Рассмотреть основную теорему о разложении на множители.
Отработать с учащимися способы разложения составного числа на множители
Ход урока: 1.Обзорная лекция.
Любое составное число с может быть записано в виде произведения c=ab, причем ни один из делителей не равен 1 и каждый из них меньше, чем с; например,
72=8*9, 150=10*15
При разложении числа с на множители один из них, и даже оба (a и b) могут оказаться составными. Если а - составное, то разложение на множители можно продолжить:
a= a1*a2 c=a1*a2*b
Примерами этого могут служить рассмотренные выше числа
72=2*4*9, 150=2*5*15.
Этот процесс разложения на множители можно продолжить до тех пор, пока он не закончится; это должно произойти, так как делители становятся все меньше и меньше, но не могут стать единицей. Когда ни один из делителей нельзя уже будет разложить на множители, то все делители будут простыми числами. Таким образом, показали, что
Каждое целое число, большее 1, является простым числом или произведением простых чисел.
Последовательное разложение числа на множители может быть выполнено многими способами. При этом можно использовать таблицу делителей. Сначала найдем наименьшее простое число p1, делящее число с, так что c=p1*c1. Если с1- составное число, то по таблице делителей найдем наименьшее простое число р2 делящее с1, так что c1 =p2*c2, c=p1*p2*c2.
Затем найдем наименьший простой делитель числа c2 и т.д.
Разложение числа на простые множители единственно.
Доказательство. Предположим, что наша теорема о единственности разложения на множители неверна. Тогда должны существовать числа, имеющие по крайней мере два различных разложения на простые множители. Выберем из них наименьшее и обозначим его через с0. Для небольших чисел, меньших 10, истинность теоремы можно установить простой проверкой. Число с0 имеет наименьший простой множитель р0, т.о. можно записать:
С0=p0*do
Так как d0<c0, то число d0 единственным образом раскладывается на простые множители. Отсюда следует, что разложение числа c0 на простые множители, содержащее число p0 единственно.
Т.к., по предположению, имеется по крайней мере два разложения числа с0 на простые множители, то должно быть разложение, не содержащее число p0. Наименьшее простое число в этом разложении обозначим через p1 и запишем c0=p1* d1.
Так как p1>p0 , то d1<d0 и, следовательно, p0d1<c0. Рассмотрим число
c'0=c0-p0d1= (p1-p0)d1
Так как оно меньше, чем число с0, то оно должно раскладываться на простые множители единственным способом; при этом простые числа c'0 состоят из простых множителей p1-p0 и d1 . Так как число с0 делится на р0, то из выражения c'0=c0-p0d1= (p1-p0)d1 следует,что число c'0 также делится р0. Следовательно, число, p0 должно быть делителем числа d1, либо p1-p0 . Но любой простой делитель числа d1 больше чем, чем p0, так как p1- наименьшее простое число в разложенииc0=p1* d1 . Таким образом, остается единственная возможность: p0 должно быть делителем числаp1-p0
и, следовательно, оно делит p1. Итак, получили противоречие, потому что p1 является простым числом и не может делиться на другое простое число p0.
Существуют разложения в которых данная теорема не выполняется. Простейшим примером может служить арифметика четных чисел
2, 4, 6, 8, 10, 12, ….
Некоторые из них могут быть разложены на два четных множителя, а другие - нет; последние называются четно-простыми числами. Это числа, которые делятся на 2, но не делятся на 4:
2, 6, 10, 14, 18, …
Очевидно, что каждое четное число является четно-простым, либо записывается в виде произведения четно-простых чисел. Но такое разложение на четно-простые числа не всегда будет единственным. Например, число 420 может быть разложено на четно-простые числа различными способами:
420= 6*70= 10*42=14*30. [28]
3.Закрепление изученного материала
-
Найдите разложение на простые множители каждого из чисел 120, 365, 1970.
-
Найдите разложение на простые множители каждого из чисел: а) год вашего рождения; б) текущий год; в) номер вашего дома.
-
Запишите все разложения числа 360 на четно простые числа. [28]
-
В каких случаях четные числа обладают единственным разложением на четно-простые множители?
-
а) Представьте в виде 2n+1 числа 1101, 1543, -1101 и -1543.
б) Можно ли представить число 1543 в виде 2n-1?
Для решений можно воспользоваться следующими свойствами (см. таблицы 1,2). Таблица 1.
-
Доказать, что сумма двух нечетных чисел четна.
Доказательство. Пусть одно число есть 2а+1, а другое 2в+1, тогда сумма (2а+1)+(2в+1)=2(а+в+1)- четное число.
-
Произведение любых двух нечетных чисел нечетно. Докажите это.
Доказательство.
(2а+1)(2в+1)=4ав+2а+2в+1=2(2а+а+в)+1.
8.а) Произведение четного числа и любого целого числа четно.
б) Четов пишет на доске одно целое число, а Нечетов - другое. Если их произведение четно, победителем объявляется Четов, если нечетно, то Нечетов. Может ли один из них играть так, чтобы непременно выиграть?
9.Если сумма двух целых чисел нечетна, то произведение этих чисел четно. Докажите это. [38].
4. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 14.Совершенные числа.
Цель: Познакомить учащихся с совершенными числами и способами их образования.
Ход урока:
1.Обзорная лекция.
Нумерология была распространенным увлечением у древних греков. Единственным объяснением этому является то, что числа в Древней Греции изображались буквами греческого алфавита, и поэтому каждому написанному слову, каждому имени соответствовало некоторое число. Люди могли сравнивать свойства чисел. соответствующих их именам.
Делители или аликвотные части чисел играли важную роль в нумерологии. В этом смысле идеальными, или, как их называют, совершенными числами являлись такие числа, которые составлялись из своих аликвотных частей, т.е. равнялись сумме своих делителей. Следует отметить, что древние греки не включали само число в состав его делителей.
Наименьшим совершенным числом является 6:
6= 1+2+3
За ним следует число 28:
28=1+2+4+7+14,
Далее число 496:
496= 1+2+4+8+16+31+62+124+ 248.
Указанные совершенные числа могут быть записаны в виде
6=2*3=2(22-1)
28= 22*7=22(23-1)
496=24*31=24(25-1)
Гипотеза: Число является совершенным. Если оно представлено в виде
Р= 2 p-1(2p-1)=2 p-1q,
q= 2p-1 является простым числом Мерсенна.
Этот результат, известный еще грекам, несложно доказать. Делителями числа P. Включая само число P, очевидно, являются следующие числа:
1, 2, 22, …, 2 p-1,
q, 2q, 22q,…, 2 p-1q.
Запишем сумму этих делителей
1+2+…+2p-1+ q(1+2+…+2p-1),
которая равна
(1+2+…+2 p-1)(q+1)=(1+2+…+2p-1)2p
Далее по формуле для суммы членов геометрической прогрессии
S=1+2+…+2p-1, умножим эту сумму на 2:
2S=2+22+…+2p-1+2p, а затем вычтем S получим S=2p-1=q.
Таким образом, сумма всех делителей числа P есть
2pq=2*2p-1q, а сумма всех делителей, кроме самого числа P= 2 p-1q, равна 2*2 p-1q-2p-1q=2p-1q=P.
Итак, число является совершенным.
Из этого результата следует, что каждое простое число Мерсенна порождает совершенное число. По мере того как натуральные числа возрастают, совершенные числа встречаются всё реже. Третье совершенное число - 496 (1+2+48+16+31+62+124+248 = 496), четвёртое - 8128, пятое - 33 550 336, шестое - 8 589 869 056, седьмое - 137 438 691 328.
Первые четыре совершенные числа: 6, 28, 496, 8128 были обнаружены более 2000 лет назад. Эти числа приведены в Арифметике Никомаха Геразского. Пятое совершенное число было выявлено лишь 500 лет назад, в 1460г. Это число 33 550 336 обнаружил немецкий математик Региомонтан (XV век). В XVI веке немецкий ученый Шейбель нашел еще два совершенных числа: 8 589 869 056 и 137 438 691 328. В начале XX века были найдены ещё три совершенных числа. В дальнейшем поиск затормозился вплоть до середины XX века, когда с появлением компьютеров стали возможными вычисления, превосходившие человеческие возможности. На апрель 2010 года известно 47 чётных совершенных чисел.
Однако и с математической точки зрения чётные совершенные числа по-
своему уникальны. Все они - треугольные. Сумма величин, обратных всем делителям числа, включая само число, всегда равна двум. Остаток от деления совершенного числа, кроме 6, на 9 равен 1. В двоичной системе совершенное число Рр начинается р единицами, потом следуют р-1 нулей. Например:
7)Р2=110, Р3=11100, Р5 =111110000, Р7 =1111111000000 и т.д.
Последняя цифра чётного совершенного числа или 6, или 8, причём, если 8, то ей предшествует 2.
Существуют ли другие виды совершенных чисел? Все числа вида Р= 2 p-1(2p-1)=2 p-1q являются четными. Существуют ли нечетные совершенные числа? В настоящее время мы не знаем ни одного такого числа, но имеется предположение, что это число должно иметь по крайней мере 36 знаков. 2.Закрепление изученного материала
-
Используя список простых чисел Мерсенна, найдите четвертое и пятое совершенные числа. [28]
3. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 15. Дружественные числа.
Цель: Познакомить учащихся с дружественными числами и рассмотреть способы их образования. Выявить отличия совершенных, фигурных, простых и составных чисел.
Ход урока:
1.Обзорная лекция.
Дружественные числа также входят в наследство, доставшееся нам от греческой нумерологии. Если у двух людей имена были таковы, что их числовые значения удовлетворяли следующему условию: сумма делителей одного равнялась второму числу, и наоборот, то считалось, что это свидетельствует об их духовной близости. В действительности греки знали всего лишь одну пару таких чисел, а именно:
220= 22*5*11. 284=22*71
Суммами их делителей являются соответственно
1+2+4+5+10+11+20+22+44+55+110=284,
1+2+4+71+142=220
Долго считалось, что следующую пару дружественных
чисел 17296 и 18416
открыл в 1636 году знаменитый французский математик
Пьер Ферма. Но недавно в одном из трактатов арабского
ученого Ибн аль-Банны (1256-1321) были найдены
строки: «Числа 17296 и 18416 являются дружественными.
Аллах всеведущ».
А задолго до Ибн аль-Банны другой арабский
математик абу-Хасан Сабит ибн Курра (836-901)
сформулировал правило, по которому можно получить
некоторые дружественные числа:
если для некоторого n
числа
p=3·2n-1-1,
q=3·2n-1
и
r=9·22n-1-1
простые,
то числа
A=2npq
и
B=2nr
- дружественные.
При n=2, числа
p=5,
q=11,
r=71 простые, и получается
пара чисел Пифагора: 220 и
284.
При n=4, числа
p=23,
q=47,
r=1151 простые, и
получается пара чисел Ибн аль-Банны и Ферма
17296 и 18416.
При n=7 получается пара
чисел, найденная в 1638 году французским математиком
и философом Рене Декартом.
После Декарта первым получил новые дружественные
числа Леонард Эйлер. Он открыл 59 пар дружественных
чисел, среди которых были и нечетные числа, например,
9773505 и 11791935.
Он предложил пять способов отыскания дружественных
чисел. Эту работу продолжили математики следующих
поколений. В настоящее время известно около 1100 пар
дружественных чисел. В 1867 году шестнадцатилетний
итальянец Николо Паганини потряс математический мир
сообщением о том, что числа 1184 и
1210 дружественные! Эту пару,
ближайшую к 220 и 284, проглядели все знаменитые
математики, изучавшие дружественные числа.
Пару чисел 220 и 284 стали считать символом
дружбы. В Средние века имели хождение талисманы с
выгравированными на них числами 220 и 284, якобы
способствующими укреплению любви.
Дружественные числа продолжают скрывать множество
тайн. Например, есть ли пары, в которых одно число
четное, а другое - нечетное? Конечно или бесконечно
число пар дружественных чисел? Существует ли общая
формула, позволяющая описать все пары дружественных
чисел?
В XX веке математики обобщили понятие
дружественных чисел и занялись поиском дружественных
рядов (или общительных чисел) -
замкнутых циклов из трех и более чисел. Например, в
тройке чисел
1 945 330 728 960; 2 324 196 638 720; 2 615 631 953920
делители первого числа в сумме дают второе число, делители второго в сумме дают третье число, а делители третьего числа в сумме дают первое число. Самый длинный из известных циклов состоит из 28 чисел, первое из которых равно 14316.
Все пары дружественных чисел до 100000 приведены в таблице 1.
Таблица 1.
Дружественные числа до 1000002.Закрепление изученного материала.
3.Подведение итогов занятия.
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 16. Наибольший общий делитель (НОД)
Цель: Рассмотреть способы получения наибольшего общего делителя. Развивать логическое мышление.
Ход урока:
1.Обзорная лекция.
Возьмем некоторую дробь a/b,
отношение двух целых положительных чисел a и b.
Сократим дробь на множители, общие для а и b. Эта
операция не изменяет значение дроби, например,
![]() .
.
Общим делителем двух натуральных
чисел a и b называется натуральное число d, которое
является множителем как числа a, так и числа b,
т.е.![]() ,
,![]() .
.
Если число d-общий делитель чисел
a и b, то он также делит числа a+b и a-b, так как
![]() ,
, ![]() .
.
Когда известны разложения чисел a и b на простые множители, нетрудно найти все их общие делители. Выпишем эти два разложения на простые множители:
![]() ,
, ![]() .
.
Запишем разложения чисел а и b
так, как если бы они имели одинаковые простые
множители p1, p2,
…,pr, но с условием, что допускаем
возможность использования показателя степени, равного
0. Например, если число p1 делит число а,
но не делит число b, полагаем, что в формуле
![]() ,
,![]()
![]() .
.
Т.о., если а=140, b=110,
то ![]() ,
, ![]() .
.
Из формулы ![]() ,
, ![]() следует, что любой
делитель a может иметь простыми множителями только
числа
следует, что любой
делитель a может иметь простыми множителями только
числа ![]() ,
которые встречаются в числе a и каждое из них
содержится в степени
,
которые встречаются в числе a и каждое из них
содержится в степени ![]()
![]() , не превосходящей
соответствующей степени
, не превосходящей
соответствующей степени ![]() в числе a.
Аналогичные условия имеют место и для любого делителя
d числа b. Поэтому общий делитель d чисел a и b может
иметь в качестве простых множителей только числа
в числе a.
Аналогичные условия имеют место и для любого делителя
d числа b. Поэтому общий делитель d чисел a и b может
иметь в качестве простых множителей только числа
![]() , которые
встречаются одновременно в числах а и b, а степень
, которые
встречаются одновременно в числах а и b, а степень
![]() числа
числа ![]() в d не может
превосходить меньшей из двух степеней:
в d не может
превосходить меньшей из двух степеней: ![]() и
и ![]() .
.
Вывод: любые два натуральных числа
а и b имеют наибольший общий делитель d0.
Простыми множителями ![]() числа d0
являются те, которые одновременно встречаются в
числах а и b, а степень числа
числа d0
являются те, которые одновременно встречаются в
числах а и b, а степень числа ![]() в числе d0
есть меньшее из двух чисел
в числе d0
есть меньшее из двух чисел ![]() и
и ![]() .
.
Пример . Возьмем два числа а=140 и
b=110, имеющие разложения на простые множители
![]() ,
, ![]() ; очевидно, что
; очевидно, что
![]() .
.
Так как степень простого числа
![]() в наибольшем
общем делителе по крайней мере не меньше, чем у
любого общего делителя, получим характеристическое
свойство:
в наибольшем
общем делителе по крайней мере не меньше, чем у
любого общего делителя, получим характеристическое
свойство:
Любое общий делитель d делит наибольший общий делитель d0.
Наибольший общий делитель двух чисел настолько важен, что существует специальное обозначение:
d0=D(a, b). [28].
Признаки делимости
1.Число делится на 2 тогда и только тогда, когда оно оканчивается четной цифрой (цифры 0,2,4,6,8 - четные, цифры 1,3,5,7,9 -нечетные).
2. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3(например, число 84 делится на 3. так как сумма его цифр - 8+4=12 делится на 3).
3.Число делится на 5 тогда и только тогда, когда оно оканчивается цифрой 0 или 5 (например, число 45 делится на 5, так как оканчивается цифрой 5).
4.Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9(например, число 198 делится на 9, так как сумма его цифр 1+9+8=18 делится на 9).
5.Число делится на 10 тогда и только тогда, когда оно оканчивается цифрой 0 (например, число 60 делится на 10, так как оно оканчивается цифрой 0).
-
40,88,72,12,48,60,52,… делятся на 4.
-
41,89,75,89,50,90,… не делятся на 4
БЕЗ дополнительных вычислений можно смело утверждать, что числа 768940, 5623088, 6702372 ,67888812 ,89048, 2345609852 делятся на 4, а числа 56741, 389, 3875, 12389, 6850, 6754390 не делятся на 4.
Сформулируйте самостоятельно признак делимости натурального числа на 4.
2.Закрепление изученного материала:
1.Найдите наибольший общий делитель пар чисел: а) 360 и 1970, б) 30 и 365, в) номера вашего телефона и вашего почтового индекса.
2.Докажите, что число ![]() -иррациональное число,
используя в доказательстве теорему о единственности
разложения. [28]
-иррациональное число,
используя в доказательстве теорему о единственности
разложения. [28]
3.а) Написать все простые числа от 1 до 50.
б) Выписать все числа от 1 до 50, представляющие собой произведение двух простых чисел.
4. а) Написать все простые числа от 51 до 100.
б) Выписать все составные числа первой сотни, состоящие из произведения одного простого сомножителя, повторяющегося несколько раз.
5. а) Разложить на составные множители числа: 48; 84; 150.
б) Разложить на простые множители (делители) числа: 8; 24; 81; 96; 100; 125; 400; 512; 680; 946; 1001; 3125; 4 500; 13860.
6. Найти общие делители чисел и указать, какой из них наибольший:
1) 12 и 18 2) 18 и 54 3) 60 и 45
4) 21 и 28 5) 20 и 24 6) 72 и 63
7) 42 и 56 8) 80 и 64 9) 120 и 96
10) 96 и 192 11) 150 и 180 12) 102 и 170
13) 84 и 120 14) 12; 18 и 30 15) 26; 65 и 130. [8]
3. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 17. Взаимно простые числа.
Цель: Познакомить учащихся с взаимно простыми числами.
Ход урока:
1.Обзорная лекция.
Число 1 является общим делителем для любой пары чисел a и b. Если единица будет единственным их общим делителем, т.е d0=D(a, b)=1.
В этом случае числа a и b взаимно простые.
Пример. (39, 22)=1.
Если числа имеют общий делитель, больший единицы, то они имеют простой делитель. Итак, два числа могут быть взаимно простыми только тогда, когда они не имеют общих простых множителей. Поэтому условие d0=D(a, b)=1. означает, что числа а и b не имеют общих простых множителей, т.е. все их простые множители различны.
Возьмем некоторую дробь a/b, отношение двух целых положительных чисел a и b. Сократим дробь на множители, общие для а и b. Если d0 есть наибольший общий делитель чисел а и b, то следует
а=a0d0, b=b0d0.
Тогда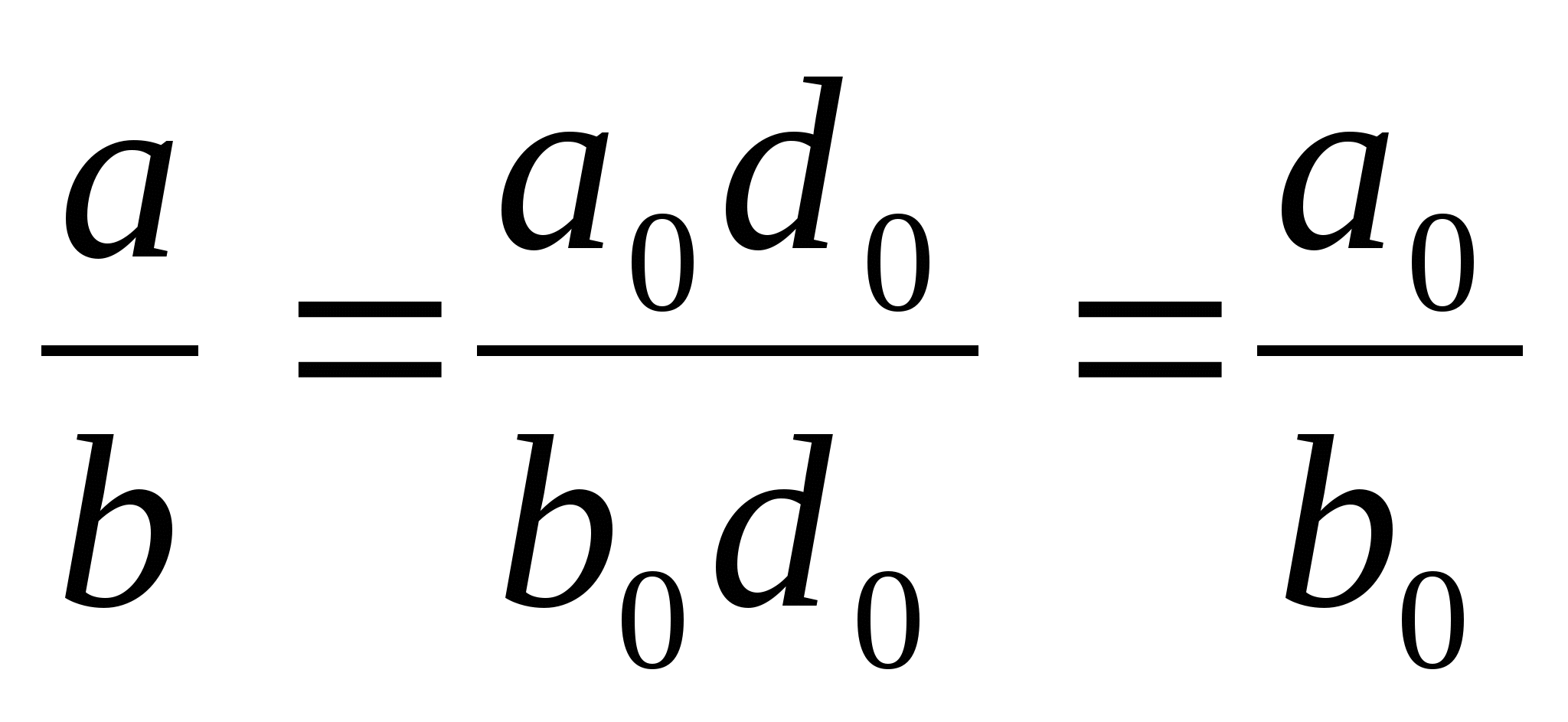 .
.
В формуле а =a0d0, b=b0d0 числа а0 и b0 не могут иметь простых общих множителей, в противном случае числа а и b имели бы общий множитель, больший, чем d0 .
Следовательно, D(a0, b0)=1
Это означает, что для второй дроби в формуле
 дальнейшее
сокращение невозможно.
дальнейшее
сокращение невозможно.
Одним из часто применяемых свойств взаимно простых чисел является следующее.
Если произведение ab делится на число c, которое взаимно просто с число b, то число a делится на с.
Доказательство. Так как число c делит произведение ab, то простые множители числа c содержатся среди простых множителей чисел а и b. Но так как D(в, b)=1, то их не может быть среди множителей числа b. Таким образом, все простые множители числа c делят число а и не делят число b, и они появляются в степенях, не меньших, чем в числе с, так как число c делит ab.
Если произведение двух взаимно простых чисел
является квадратом, ![]() , D(a, b)=1, то числа
a и b являются квадратами:
, D(a, b)=1, то числа
a и b являются квадратами:
![]() ,
, ![]() .
.
Доказательство. Для того чтобы некоторое число
было квадратом, необходимо и достаточно, чтобы все
степени в разложении его на простые множители были
четными. Так как числа a и b - взаимно простые
![]() , D(a, b)=1, то
любой простой множитель из c2 содержится либо в a,
либо в b, но не в обоих; отсюда простые множители
чисел a и b должны иметь четные степени. [28].
, D(a, b)=1, то
любой простой множитель из c2 содержится либо в a,
либо в b, но не в обоих; отсюда простые множители
чисел a и b должны иметь четные степени. [28].
2.Закрепление изученного материала:
1.Какие числа взаимно простые с числом 2?
2. Почему D(n,n+1)=1?
3. Исследуйте пары дружественных чисел и найдите те из них, которые взаимно просты.
4. Может ли правило, выраженное в формулах
![]() , D(a, b)=1,
, D(a, b)=1,
![]() ,
, ![]() , быть справедливым не
только для квадратов. Но и для произвольных степеней?
, быть справедливым не
только для квадратов. Но и для произвольных степеней?
5. Написать несколько составных чисел, которые были бы взаимно простыми между собой.
6. Написать по два взаимно простых числа числам:8; 20; 84.
3. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 18-19. Алгоритм Евклида.
Цель: Познакомить учащихся с алгоритмом Евклида. Рассмотреть два способа записи алгоритма Евклида. Развивать способность самостоятельного поиска ответов на вопросы.
1.Обзорная лекция.
Рассмотрим дробь a/b. Если a>b, то дробь является целым числом, большим 1, то дробь представляем в виде смешанного числа, т.е. целой и дробной части, меньшей единицы.
Примеры.![]() ,
,
![]() .
.
В общем случае используем деление с остатком чисел
a и b ![]() , а
именно:
, а
именно:
![]() ,
где
,
где![]() .
.
Очевидно, что это всегда возможно. Действительно, рассмотрим числа 0, 1, 2, … на числовой прямой (рис.1).

Рис.1.
На числовой прямой расположим число а. Начиная от
точки 0 отметим точки b, 2b,3b и т.д. до точки qb
такой что, qb не больше, чем a, в то время как (q+1)b
уже больше a. Расстояние от точки qb до точки a и
есть r. Число r - остаток при делении, а q- частное.
Частное q имеет специальное обозначение:![]() . Этот символ
обозначает наибольшее целое число, не превосходящее
числа a/b. Для примеров, приведенных выше получим
. Этот символ
обозначает наибольшее целое число, не превосходящее
числа a/b. Для примеров, приведенных выше получим
![]() ,
,![]() .
.
Если a=qb+r, ![]() , то D(a
,b)=d=D(r ,b).
, то D(a
,b)=d=D(r ,b).
Доказательство. Запишем d0=D(r,b), d1=D(r,b). (1)
Таким образом, доказательство соотношения (1), означает доказательство того, что d0= d1. Любой общий делитель чисел a и b также делит число
r=a-qb.
Следовательно, число r делится на d0.
Так как число d0 является делителем
числа r, так и числа b, то оно должно делить и число
d1=D(r,b); отсюда ![]() . С другой стороны, в
соответствии с соотношением a=qb+r,
. С другой стороны, в
соответствии с соотношением a=qb+r,
![]() любой общий
делитель чисел r и b делит число a. Так как число
d1 делит также и число b, то оно должно
делить и числоd0=D(r,b), следовательно,
любой общий
делитель чисел r и b делит число a. Так как число
d1 делит также и число b, то оно должно
делить и числоd0=D(r,b), следовательно,
![]() . Из сказанного
следует, что
. Из сказанного
следует, что ![]() .
.
Пример, ![]() ;
следовательно, (1066, 200)=(66, 200).
;
следовательно, (1066, 200)=(66, 200).
Этот результат, сформулированный в утверждении
d0=D(r,b), d1=D(r,b), дает
простой метод вычисления наибольшего общего делителя
двух чисел. Вместо поисков наибольшего общего
делителя чисел a и b достаточно найти наибольший
общий делитель чисел r и b.Эта задача более проста,
чем каждое чисел a и b. Что бы найти наибольший общий
делитель чисел r и b, разделим число b на r:![]() , где r1 меньше
каждого из чисел b и r. В соответствии с правилом
D(a,b)=d=D(r,b) получаем
, где r1 меньше
каждого из чисел b и r. В соответствии с правилом
D(a,b)=d=D(r,b) получаем ![]() .
.
Далее, таким же способом обращаемся с числами r и
r1 и т. д. В результате получаем последовательность
пар чисел, каждая из которых имеет один и тот же
наибольший общий делитель: ![]()
Так как остатки постоянно уменьшаются, то эта
последовательность должна закончиться после получения
остатка ![]() . Это
происходит при делении
. Это
происходит при делении![]() , т.е число
rk делит число r
k-1. Тогда
, т.е число
rk делит число r
k-1. Тогда ![]() , из
, из
![]() видно, что
видно, что
![]() .
.
Другими словами, число d0 равно первому из остатков, который делит предшествующий ему остаток.
Пример 1. Найти наибольший общий делитель чисел 1970 и 1066.
Решение. Разделим одно число на другое.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следовательно, (1970, 1066)=2.
Этот метод нахождения наибольшего общего делителя двух чисел называется алгоритмом Евклида, так как первое его описание содержится в «Началах» Евклида. ... = au + bv = ( a , b ).
Пример 2. Найти НОД: а = 525, b = 231.(запись деления уголком, и каждый раз то, что было в уголке, т.е. делитель, приписывается к остатку от деления с левой стороны, а остаток, как новый делитель, берется в уголок)Запись в виде цепочки равенств:
525 = 231 · 2 + 63
231 = 63 · 3 + 42
63 = 42 · 1 + 21
42 = 21 · 2
Таким образом, (525, 231) = 21. Линейное представление наибольшего общего делителя:
21 = 63 - 42 · 1 = 63 - (231 - 63 ·
3) · 1 =
= 525 - 231 · 2 - (231 - (525 - 231 · 2) · 3) =
= 525 · 4 - 231 · 9. [28].
2.Закрепление изученного материала.
-
Найдите наибольший общий делитель пар чисел, используя алгоритм Евклида.
а) 360 и 1970, б) 30 и 365, в) номера вашего телефона и почтового индекса.
2. Найдите НОД для каждой из пяти первых дружественных чисел. Сравните результат с результатами, полученными с помощью разложения на простые множители (фронтальная работа). [28]
3.Найдите НОД с помощью алгоритма Евклида (данное упражнение можно выполнить как самостоятельно, так фронтально):
1) 1231, 1672; 2) 132, 21; 3) 135, 8211; 4) 549, 387; 5) 589, 343; 6 ) 12606, 6494;
7) 29719, 76501; 8) 162891, 32176; 9) 469459, 519203; 10) 738089, 3082607;
11) 179370199, 4345121; 12)3327449, 6314153; 13) 12870, 7650; 14) 41383, 103818;
15) 3640, 14300; 16) 24700, 33250.
4. Найдите НОД для следующий трех чисел (данное упражнение можно выполнить как самостоятельно, так фронтально, так и раздать карточки по усмотрению учителя):
1) 420, 126, 525; 2) 529, 1541, 1817; 3) 67283, 122433, 221703; 4) 549493, 863489, 2133125; 5) 738089, 3082607, 28303937; 6) 1767, 2223, 11913; 7) 476, 1258, 21114; 8) 3445, 4225, 5915.
5.Найдите НОД 111111 и 111111111.
6.Найдите НОД чисел 121212 и 121212121212.
7. Найдите трехзначное число, если оно при делении на 7, 11 и 13 дает соответственно остатки 5, 9 и 11. (Задания 5-7 можно предложить сильным учащимся). [8]
8. Сократите дробь (данное задание можно предложить в качестве домашнего задания)
1)![]() ;
2)
;
2)![]() ; 3)
; 3)
![]() ; 4)
; 4)![]() ; 5)
; 5) ![]() ; 6)
; 6)![]() ; 7)
; 7)![]() ; 8)
; 8)![]()
9)![]() ; 10)
; 10)
![]() . [18]
. [18]
3. Подведение итогов занятия:
- Интересными ли явились задания?
- Не являются ли они сложными или, наоборот, простыми?
Выставление учениками самим себе баллов за каждое верно решенное задание (1 зад. - 1 балл).
Занятие 20. Наименьшее общее кратное.
Цель: рассмотреть способы получения наименьшего общего кратного.
Развивать абстрактное и логическое мышление.
Ход урока:
1.Обзорная лекция.
Рассмотрим дроби ![]() и
и ![]() .
.
Чтобы сложить (вычесть) две дроби с разными знаменателями, то их необходимо привести к общему знаменателю, а затем складываем (вычитаем) числители.
Пример:![]() .
.
Вообще, чтобы получить сумму
![]() +
+![]() , должны найти общее
кратное для чисел a и b, т.е. число m, на которое
делятся как число a, так b. Одно из таких чисел
очевидно, а именно, их произведение m=ab; в
результате получаем в качестве суммы дробей
, должны найти общее
кратное для чисел a и b, т.е. число m, на которое
делятся как число a, так b. Одно из таких чисел
очевидно, а именно, их произведение m=ab; в
результате получаем в качестве суммы дробей
![]() .
.
Но существует бесконечно много других общих кратных для чисел a и b. Предположим, что знаем разложение этих двух чисел на простые множители:
![]() ,
, ![]() (1).
(1).
Число m, которое делится одновременно на числа a и
b, должно делиться на каждый простой делитель
![]() чисел a и b и
содержать его в степени
чисел a и b и
содержать его в степени ![]() не меньшей, чем
большая из двух степеней
не меньшей, чем
большая из двух степеней ![]() и
и ![]() . Таким образом, среди
общих кратных существует наименьшее
. Таким образом, среди
общих кратных существует наименьшее ![]() , в котором каждый
показатель степени
, в котором каждый
показатель степени ![]() равен большему из
чисел
равен большему из
чисел ![]() и
и
![]() . Очевидно, что
число
. Очевидно, что
число ![]() . Для
наименьшего общего кратного существует специальное
обозначение
. Для
наименьшего общего кратного существует специальное
обозначение![]() .
.
Пример. a=140, b=110. Разложение на простые множители этих чисел таково:
![]() ,
, ![]() , следовательно,
, следовательно,
![]() .
.
Существует следующее простое соотношение между наибольшим общим делителем и наименьшим общим кратным: ab=D(a,b)K(a,b).
Доказательство. Перемножив два числа из (1)
получим ![]() .
.
Как отмечала, степень числа ![]() в D(a,b) является
меньшей из двух чисел
в D(a,b) является
меньшей из двух чисел ![]() и
и ![]() , в числе K(a,b) она
большая из них. Предположим, что
, в числе K(a,b) она
большая из них. Предположим, что ![]()
![]()
![]() . Тогда степень числа
. Тогда степень числа
![]() в числе D(a,b)
равна
в числе D(a,b)
равна ![]() , а в
K(a,b) равна
, а в
K(a,b) равна ![]() ;
следовательно их произведения
;
следовательно их произведения
D(a,b) K(a,b) она равна ![]() +
+![]() , что в точности
равняется степени в произведении
, что в точности
равняется степени в произведении
![]() . Это
показывает справедливость соотношения
ab=D(a,b)K(a,b).
. Это
показывает справедливость соотношения
ab=D(a,b)K(a,b).
Пример. a=140, b=110, D(a,b)=10, K(a,b)=1540.
![]() D(a,b) K(a,b).
D(a,b) K(a,b).
Из правила вытекает, что если a и b взаимно простые, то их произведение равно их наибольшему общему кратному; действительно, в этом случае D(a,b)=1 и поэтому ab= K(a,b). [28]
2.Закрепление изученного материала:
1.Найдите наибольшее общее кратное пар чисел.
а) 360 и 1970, б) 30 и 365, в) номера вашего телефона и почтового индекса.
2. Найдите НОК для каждой из четырех первых дружественных чисел. [28]
3. Написать несколько чисел, кратных 2 и 3; 3 и 7; 2, 5 и 11; 3, 5 и 7.
4. Написать несколько общих кратных для чисел: 5 и 15; 8 и 12; 20 и 25; 24 и 36.
5.Найти наименьшее общее кратное чисел:
1) 2 и 5 2) 3 и 7 3) 9 и 10
4) 14 и 25 5) 15 и 18 6) 24 и 36
7) 45 и 75 8) 100 и 120 9) 10; 21 и 23
10) 56; 70 и 126 11) 54; 90 и 162 12) 40; 60; 100 и 150.
6.Найти наименьшее общее кратное чисел:
1) 2 и 3 2) 3 и 11 3) 4 и 9
4) 10 и 21 5) 12 и 15 6) 25 и 45
7) 16 и 56 8) 25 и 75 9) 8; 15 и 19
10) 26; 51 и 78 11) 63; 126 и 252 12) 54; 81; 135 и 189.
7.Найти наименьшее общее кратное чисел и дополнительные множители к ним.
1) 154 и 210 2) 120 и 144 3) 255 и 510
4) 35 и 55 5) 105 и 165 6) 120 и 192
7) 12; 18 и 108 8) 60; 72 и 75 9) 240; 360 и 900
10) 50; 125 и 175 11) 210; 84 и 45 12) 450; 855 и 950.
8.Найти наименьшее общее кратное чисел и дополнительные множители к ним.
1) 66; 110 и 154 2) 42; 63 и 105 3) 60; 75 и 135;
4) 160; 240 и 2 000 5) 156; 195 и 3 900 6) 40; 64; 112 и 88.
1) 2 и 5 2) 3 и 7 3) 9 и 10
4) 14 и 25 5) 15 и 18 6) 24 и 36
7) 45 и 75 8) 100 и 120 9) 10; 21 и 23
10) 56; 70 и 126 11) 54; 90 и 162 12) 40; 60; 100 и 150.
(Задания 1-6 выполнить фронтально, задание 7- индивидуально, задание 8- можно выполнить в качестве домашнего задания).
Занятие 21-22. Зачет.
Цель: выявить уровень овладения учащимися знаниями и умениями на элективном курсе
Ход занятия: 1. Организационный момент. Работа составлена по типу контрольно-измерительных материалов единого государственного экзамена
-
Проверка уровня знаний и умений, уровня познавательной самостоятельности учащихся. Итоговая контрольная работа
Вариант 1- четные номера, Вариант 2- нечетные номера.
Часть 1.
1.Какое из чисел является делителем 36? 1) 8 2)12 3)24 4)72
2.Какое из чисел не является делителем 50? 1)5 2)10 3)20 4)50
3.Какое число является кратным 36? 1)9 2)18 3)48 4)72
4.Какое из чисел является делителем 36 и кратным 6? 1)24 2)12 3)9 4) 72
5.Какое из чисел не является кратным 3? 1) 15 2)27 3)35 4)45
6. Сколько натуральных делителей имеет число 12?
7.Сколько четных чисел удовлетворяют неравенству 11<x<20?
8.Какие цифры надо поставить вместо *, чтобы число 543* делилось на 2?
9.Какие цифры надо поставить вместо *, чтобы число 542* делилось на 3?
10.Какие цифры надо поставить вместо *, чтобы число 543* делилось на 5?
11.Какую цифру надо поставить вместо *, чтобы число 542* делилось 6?
12.Какую цифру надо поставить вместо*, чтобы число 541* делилось на 15?
13.Остаток от деления числа 94 на 7 равен
1)3 2)4 3)5 4)6
14.Частное от деления числа 94 на 7 равно
1)11 2)12 3)13 4)14
15.Наибольший общий делитель чисел а=2*3*3 *3*5*5 в=2*3*3*5*5*5
1)5 2)2*3*5 3)2*2*3*3*5*5 4)2*3*5*5*3
16.Наименьшее общее кратное чисел а=2*3*5*5 и в=2*2*3*5 равно
1)2*2*2*3*3*5*5*5 2)2*3*5 3)2*2*3*3*5*5 4)2*2*3*5*5
Часть 2.
17.Докажите что сумма 25+43+83 делится на 19.
18.Докажите, что делится ![]() на 17.
на 17.
19.найдите последнюю цифру числа 11*12*13*14*15.
20.Разложите на простые множители число 360.
21. Разложите на простые множители число 792.
22.Найдите наибольшее кратное чисел 180 и 270.
23.Найдите наибольший общий делитель чисел 180 и 270.
24.Найдите наименьшее общее кратное чисел 168 и 450.
25.Найдите наибольший общий делитель чисел 168 и 450.
26.Сократите дробь. ![]()
27.Сократите дробь.![]()
![]()
28.Какие простые числа являются решениями неравенства 18<x<27?
29.Сколькими способами можно разложить на два натуральных множителя число 12? Способы, при которых произведения отличаются только порядком множителей, считаются за один способ.
Задания на 3.
30. Найдите последнюю цифру числа 3100.
31.Остаток от деления некоторого натурального числа на 16 равен 9. Найдите остаток от деления этого числа на 4.
32.Остаток от деления некоторого натурального числа на 4 равен 1. Найдите остаток от деления этого числа на 16.
33. При делении на 12 число а дает остаток
7. Какой остаток получится при делении на 12 числа
![]() .
.
34.При делении на 5 одно целое число дает остаток 2, а другое - остаток 4. Найдите остаток от деления на 5 суммы этих чисел.
35.При делении на 5 одно целое число дает остаток 2, а другое - остаток 4.Найдите остаток от деления на 5 произведения этих чисел.
36. Сколько натуральных делителей имеет число
![]() ?
?
37.Найдите все четырехзначные числа, в записи которых входят только цифры 1,2 и которые делятся и на 2, и на 3.
38.Какую цифру надо приписать к числу 14 слева и справа, чтобы получилось число делящееся на 3?
39.Вдоль дороги от деревни Видное поставили столбы через каждые 48 метров. Эти столбы решили заменить другими, поставив их на расстоянии 60 метров друг от друга. Найдите расстояние от деревни Видное до ближайшего столба, которых будет стоять на месте старого.
40.Пакет сока стоит 19р.50к. Какое наибольшее число таких пакетов можно купить на 220 р.?
41. Для учащихся третьего класса приготовили одинаковые подарки. Во всех было 120 блокнотов, 280 ручек и 320 карандашей. Сколько учащихся в классе, если известно, что их больше 30 человек?
Задания на 4 балла.
42.Может ли при делении квадрата натурального числа на 4 получиться остаток 2?
43.Докажите, что на прямой 2х+4у=3 нет ни одной точки с целочисленными координатами.
44.Остаток от деления некоторого натурального числа на 6 равен 3, остаток от деления этого же числа на 15 равен 1. Найдите остаток от деления этого числа на 30.
45.Найдите все пары натуральных чисел,
удовлетворяющих уравнению ![]() .
.
46.Найдите все пары натуральных чисел,
удовлетворяющих уравнению ![]()
![]() .
.
47.На складе есть шоколадки двух видов: стоимостью 9 р. И стоимостью 15р. Может ли стоимость всех шоколадок быть равной 2009 р.?
48.найдите периметр треугольника, если длины двух его сторон равны 1 см и 9 см, а длина третьей стороны является натуральным числом.
49.На графике ![]()
![]() найдите все такие
точки, абсциссы и ординаты которых являются
натуральными числами.
найдите все такие
точки, абсциссы и ординаты которых являются
натуральными числами.
50.В книге пронумеровали все страницы от 1 до 45. Сколько раз использовали цифру 3?
Учащимся предлагается пройти компьютерное тестирование по теме «Теория чисел». В работе представлено четыре задания уровня А, с выбором ответа, пять заданий уровня Б, где требуется написать свой ответ. Выполнение данных упражнений осуществляется с помощью компьютера. Подводится предварительный итог. Далее учащиеся на отдельном листе выполняют два задания уровня С, где требуется привести подробное решение. После их проверки учителем выставляется итоговая оценка.
3. Подведение итогов урока.
Ученикам сообщается, что окончательные результаты работы будут объявлены на следующем занятии.
Выясняется мнение учеников о проведенной зачетной работе.
Уравнение с двумя переменными и его график
9 класс
Тип урока:
Урок изучения нового материала с использованием ИКТ
Цели урока:
Образовательная:
-
Расширить представление о способах решения уравнений.
-
Сформировать умение решать уравнения графическим способом.
Развивающая:
-
Работать над развитием понятийного аппарата;
-
Развивать навыки самоконтроля.
-
развивать логическое мышление, способность к абстрагированию, анализу.
Воспитательная:
-
Воспитывать ответственное отношение к труду;
-
Воспитывать волю и настойчивость для достижения конечных результатов.
Оборудование:
-
АРМ
-
Доска
-
Листы рефлексии
-
Поэтапное описание работы
Программное обеспечение:
1.Microsoft Power Point
Этапы урока:
1. Организационный момент.
2. Актуализация опорных знаний.
3. Исследовательская работа по добыванию новых знаний
4. Физкультминутка
.
5. Первичное закрепление материала. Тренировочные упражнения.
6. Итог урока. Постановка домашнего задания.
7. Рефлексия урока
Ход урока:
I. Организационный момент.
Проверка готовности учащихся к уроку
Рефлексия настроения.
На листах рефлексии делают выбор одной из геометрических фигур, которые характеризуют их настроение на каждом этапе урока
II. Актуализация опорных знаний.
1. Укажите виды уравнений и найдите среди них лишнее
1![]() .
.
![]()
2![]() .
.
3![]() .
.
4![]() .
.
5.
III.Изучение нового материала
Примеры уравнений с двумя переменными
-
Уравнения х (х - у) = 4,
-
2у - х2 = - 2,
-
х (х + у2) = х + 1
-
могут служить примерами уравнений с двумя переменными.
3.Подставим в уравнение
х (х - у) = 4
-
Вместо х значение(-1), а вместо у - значение 3,
-
-1-(-1-3) = 4.
-
4=4
-
Получилось верное равенство.
-
Пара (-1; 3) значений переменных х и у является решением уравнения
х(х - у) = 4.
Определение.
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Уравнение с двумя переменными имеет, как правило, бесконечно много решений.
Пример 1.Является ли пара чисел (-1;-8) решением уравнения x2 +y2=62
(-1)2+(-8)2=62
65=62 (л)
Пара (-1; -8) не является решением уравнения
x2 +y2=62
Определение равносильности двух уравнений.
-
Два уравнения, имеющие одно и то же множество решений, называют равносильными уравнениями.
-
Л
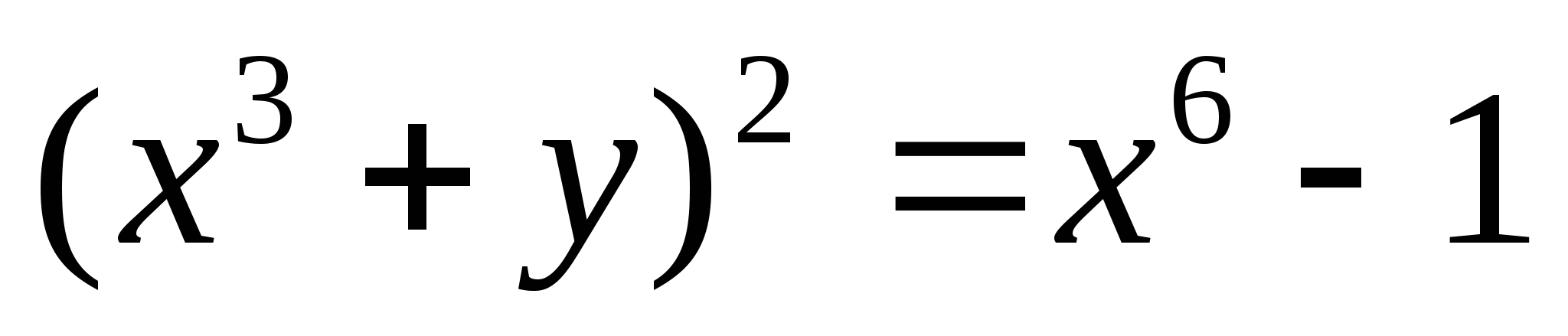 юбое целое
уравнение с двумя переменными можно заменить
равносильным уравнением, в котором правая часть
будет нулем, а левая - многочленом стандартного
вида.
юбое целое
уравнение с двумя переменными можно заменить
равносильным уравнением, в котором правая часть
будет нулем, а левая - многочленом стандартного
вида.
Например, уравнение
р![]() авносильно
авносильно
уравнению , и значит, является уравнением четвертой степени.
Определение графика функции.
Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство.
Графики каких функций изображены на чертежах?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Как решить уравнение графическим способом?
Алгоритм решения уравнений графическим способом.
-
Преобразовать данное уравнение, чтобы обе части можно было рассмотреть как функции.
-
Построить в одной системе координат графики полученных функций.
-
Найти абсциссы точек пересечения графиков или установить, что их нет.
Учащиеся могут выдвигать предположения, ставится проблемный вопрос
Выполняют устные упражнений. Фронтальная работа.
Работа с
презентацией.
Выбирается уравнение, которое содержит две переменные. Ответ обосновывается.
Учащиеся записывают примеры уравнений с двумя переменными.
Учащиеся
проверяют, является данная точка решением уравнения.
Запись определений в тетради учащихся.
Ученики проверяют является пара чисел решением уравнения.
Запись в тетради учащихся определения равносильности.
Ученики определяют степень предложенных уравнений, обосновывая свои ответы.
Запись определения в тетрадях учащихся.
Учащиеся рассматривают графики данных функции, определяют аналитическую запись (уравнения, формулы).
Ученики предлагают способы решения уравнений с двумя переменными графически.
Запись алгоритма решения уравнений графическим способом в тетради.
III. Физкультминутка.
Упражнение: «Точка. Прямая. Плоскость»
Выполняется сначала правой рукой, потом левой, затем обеими одновременно. На парту кладётся кисть руки, согнутая в кулаке (большой палец зажат в кулаке) - «точка»; меняем положение кисти и кладём ладонь ребром - «прямая»; раскрытая ладонь кладётся на парту - «плоскость»
Кинезеологические упражнения активизируют работу правого и левого полушария головного мозга. Делается по 5 повторений.
III. Исследовательская работа по изучению взаимного расположения графиков .
Работа выполняется в парах. На каждой парте поэтапное описание работы. Учащиеся выполняют работу, выдвигают гипотезы, проверяют решение с помощью слайда презентации, делают выводы.
VI. 6. Итог урока. Постановка домашнего задания. Рефлексия.
Тремя предложениями выразить содержание урока:
-
На данном уроке говорилось о …
-
Открытием для меня стало…
-
Сегодня я понял(а), что…
С каким настроение вы уходите с урока?
Учащиеся записывают задание в дневники.
Несколько учащихся продолжают фразу.
Заполняется Лист рефлексии
Занятия 23-30.Уравнеине в целых числах.
Цель: формирование умения решать уравнения целых числах; развитие умения анализировать, обобщать, систематизировать.
Ход занятия:
1.Организационный момент.
2. Проверка домашнего задания. На доске записаны ответы к домашнему заданию. Ученики проверяют свои полученные ответы. Если у большинства ответ не верный, то задание разбирается подробно, иначе, те, кто не справился, обращаются после занятия за помощью к одноклассникам.
3.Обзорная лекция:
-
Применение теории делимости к решению неопределенных уравнений в целых числах.
Неопределенные уравнения - уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.
Для решения в целых числах уравнения вида ах + by = c, где а, b, c - целые числа, отличные от нуля, приведем ряд теоретических положений, которые позволят установить правило решения. Эти положения основаны также на уже известных фактах теории делимости.
Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.
(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)
Доказательство теоремы основано на использовании равенства алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (наибольший общий делитель выражается через неполные частные и остатки, начиная с последнего равенства в алгоритме Евклида).
Пример.
Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.
Решение.
1. Составим равенства алгоритма Евклида:
1672 = 1232 ∙1 + 440,
1232 = 440 ∙ 2 + 352,
440 = 352 ∙ 1 + 88,
352 = 88 ∙ 4, т.е. (1672,352) = 88.
2) Выразим 88 последовательно через неполные частные и остатки, используя полученные выше равенства, начиная с конца:
88 = 440 - 352∙1 = (1672 - 1232) - (1232 - 1672∙2 + 1232∙2) = 1672∙3 - 1232∙4, т.е. 88 = 1672∙3 + 1232∙(-4).
Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.
Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + bу = 1, если НОД (а, в) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.
Пример.
Найти целое решение уравнения 15х + 37у = 1.
Решение.
1. 37 = 15 ∙ 2 + 7,
15 = 7 ∙ 2 + 1.
2. 1 = 15 - 7∙2 = 15 - (37 - 15∙2) ∙2 = 15∙5 + 37∙(-2),
т.е. х = 5, у= -2 - решение данного уравнения.
Теорема 3. Если в уравнении ах + bу = с НОД (а, b) = d >1 и с не делится на d, то уравнение целых решений не имеет.
Для доказательства теоремы достаточно предположить противное.
Пример.
Найти целое решение уравнения 16х - 34у = 7.
Решение.
(16,34)=2; 7 не делится на 2, уравнение целых решений не имеет.
Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с>d, то оно равносильно уравнению ах + bу = с, в котором НОД(а, b) = 1.
При доказательстве теоремы следует показать, что произвольное целое решение первого уравнения является также решением второго уравнения и обратно.
Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:
х = хс + bt, у = yc-at, где х, y - целое решение уравнения ах + bу = 1,
t - любое целое число.
При доказательстве теоремы следует показать, во-первых, что приведенные формулы действительно дают решения данного уравнения и, во-вторых, что произвольное целое решение этого уравнения заключено в приведенных формулах.
Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах+ bу = с НОД(а, b) = 1:
-
Находится целое решение уравнения ах + bу = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
-
Составляется общая формула целых решений данного уравнения х = хс + bt, у = yc - at, где х, y - целое решение уравнения ах + bу = 1, t - любое целое число.
Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т.д.
Пример.
Найти целые решения уравнения 407х - 2816у = 33.
Решение.
1. Упрощаем данное уравнение, приводя его к виду 37х - 256у = 3.
2.Решаем уравнение 37х - 256у = 1.
256 = 37∙ 6 + 34,
37 = 34 ∙1 + 3,
34 = 3 ∙11 + 1.
1 = 34 - 3∙11 = 256 - 37∙6 - 11 (37 - 256 + 37∙6) = 256∙12 - 37∙83 =
= 37∙(-83) - 256∙(-12),
т.е. х= -83, y= -12.
3. Общий вид всех целых решений данного уравнения:
х = -83∙3 - 256t = -249 - 256t,
у = -12∙3 - 37 t = -36 - 37 t.
Положив t = -1, получим х= 7, у= 1 и общие формулы решений примут вид: х = 7 - 256t, у = 1-37t. [7]
2.Закрепление изученного материала.
Задача 1. имеются контейнеры двух видов на 130 кг и 160 кг. Сколько было контейнеров первого и второго вида, если они вместе весят 3 тонны. Укажите все решения.
Решение. Обозначим количество контейнеров первого вида через x, второго через y. Получаем уравнение.
130х+160у=3000
13х+16у=300
Попробуем воспользоваться делимостью на 13. Для этого 16у представим в виде 13у+3у. а 300 разделим на 13 с остатком.
13х+13у+3у=13*23+1; 3у-1=13*23-13х-13у
Первая часть последнего уравнения делится на 13, следовательно, и левая часть должна делится на 13. Для того чтобы найти значения у, при которых разность 3у-1 делится на 13, применим перебор.
При этом проще не придавать последовательные значения 1,2,3 и т.д., а приравнивать 3у-1 к числам делящимся на 13: 13, 26, 39, 52,65 и т.д. выясняя каждый раз, является ли корень соответствующего уравнения целым или дробным. Целые корни получаются в следующих случаях: 3у-1=26; у=9; 3у-1=65; у=22 и др.
Но уже при значении у=22 слишком велико, т.к. в этом случае 16у=16* 22=352>300.
При у=9 из уравнения можно найти х:
13х+16*9=300; 13х=156; х=12.
Ответ: 12 контейнеров по 130 кг и 9 по 160 кг.[8]
Задача 2. Найдите наименьшее натуральное число, которое делится на 28, а при делении на 15 дает в остатке 4.
Решение. Искомое число равно, с одной стороны, 28х, а с другой- 15у+4. где х и у -натуральные числа. Получаем уравнения 28х=15у+4.
Не нужно искать все решения этого уравнения в натуральных числах х, а только одно решение-то, для которого значения х и у минимальны. Для этой цели преобразуем уравнение, используя признак делимости на 15.
30х-2х=15у+4, 30х-15у=4+2х, откуда (2х+4):15, (х+2):15.
Поскольку нам требуется наименьшее значение х, удовлетворяющее последней делимости, то х+2 приравняем к 15:
Х+2=15, х=13. Ответ: 364. [8]
Задача 3.
«Шли сорок мышей, несли сорок грошей,
Две мыши несли по два гроша,
Немало мышей - вообще без грошей.
Большие совсем тащили по семь.
А остальные несли по четыре.
Сколько мышей шли без грошей?»
(И.Акулич. «Квант», №4, 1995).
Обозначим количество мышей, которые шли без грошей, через х, количество больших мышей - через у, а количество тех, которые несли по четыре гроша, - через z. Составим систему уравнений с неизвестными х, у и z:
![]()
![]()
Эта система двух линейных уравнений с тремя неизвестными.
Для ее решения учтем, что на основании первого
уравнения у делится на 4. Кроме того, ![]() ;
; ![]() .
.
Откуда ![]() .
Такое у только одно: у=4. Тогда из первого уравнения
находим z, а затем из второго х:
.
Такое у только одно: у=4. Тогда из первого уравнения
находим z, а затем из второго х:
![]() ; 4z=8, z=2,
х+4+2=38, х=32. Ответ: 32. [8].
; 4z=8, z=2,
х+4+2=38, х=32. Ответ: 32. [8].
Задача 4.
Найдите все решения уравнения 5х-7у=3 в целых числах.
Решение. Выразим из уравнения то неизвестное, коэффициент при котором меньше по модулю - в данном случае х:
5х=7у+3, ![]() .
.
В числителе полученной дроби 7у разобьем на два слагаемых, одно из которых при любом целом у делится на 5, а у другого коэффициент меньше 5: 7у=5у+2у. Затем числитель дроби разделим почленно на знаменатель:
![]() .
.
Дробь![]() должна быть равна целому числу. Положим где z- целое.
Тогда 2у+3=5z.
должна быть равна целому числу. Положим где z- целое.
Тогда 2у+3=5z.
Получилось новое уравнение первой степени с двумя неизвестными, но с меньшими по модулю коэффициентами.
Из последнего уравнения выразим то неизвестное, коэффициент которого меньше по модулю, в данном случае у, и проделаем аналогичные преобразование:
![]() ,
, ![]() .
.
До каких пор продолжать такую процедуру. В общем
случае- до тех пор, пока не получится уравнение, у
которого коэффициент при одном из неизвестных равен 1
или -1. В данном случае она уже заканчивается. Дробь
![]() должна быть целым
числом. Обозначим его через t:
должна быть целым
числом. Обозначим его через t:
![]() , z+3=2t,
z=2t-3, где t- целое число.
, z+3=2t,
z=2t-3, где t- целое число.
Выразим у и х через t.![]()
![]() .
.
Получили формулы х=7t-12, у=5t-9
Здесь t - целое число. Но является ли t любым целым числом? Для ответа на вопрос подставим выражения для х и у в левую часть исходного уравнения:
![]() .
.
Следовательно, это формулы, где t- любое число, дают множество всех решений уравнения в целых числах.
Придавая t, например, значения 0, 1 и 2, получаем частные решения уравнения: (-12;-9), (-5;-4), (2;1). Ответ: х=7t-12,y=5t-9, где t любое целое число. [8].
Задачи для самостоятельного решения:2. Метод полного перебора всех возможных значений переменных, входящих в уравнение.
Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49х + 51у = 602.Решение: Выразим из уравнения переменную х через у х =, так как х и у - натуральные числа, то х = 602 - 51у ≥ 49, 51у≤553, 1≤у≤10.
Полный перебор вариантов показывает, что натуральными решениями уравнения являются х=5, у=7.Ответ: (5;7). [8].
4. Подведение итогов.- Какова была тема занятия? Что нового узнали на занятии?
- Достигли ли цели, поставленной в начале занятия? Выставление учениками самим себе баллов за каждое верно решенное задание (1 задание - 1 балл).
Занятие 31-32. Зачет.
Цель: выявить уровень овладения учащимися знаниями и умениями на элективном курсе
Ход занятия:1. Организационный момент.
Работа составлена по типу контрольно-измерительных материалов единого государственного экзамена, который предстоит пройти по окончании школы.
Учащимся предлагается пройти компьютерное тестирование по теме «Теория чисел». В работе представлено четыре задания уровня А, с выбором ответа, пять заданий уровня Б, где требуется написать свой ответ. Выполнение данных упражнений осуществляется с помощью компьютера. Подводится предварительный итог. Далее учащиеся на отдельном листе выполняют два задания уровня С, где требуется привести подробное решение. После их проверки учителем выставляется итоговая оценка.
2. Проверка уровня знаний и умений, уровня познавательной самостоятельности учащихся. Итоговая контрольная работа
Вариант 1.
1. решить уравнение в целых числах 5х+63у=-1.
2. определите целые положительные значения коэффициентов а и в в уравнении ах+ву=58, при которых х=5, у=4.
Вариант 2.
1. решить уравнение в целых числах 9х+4у=43.
2. разложите число 100 на 2 части так, чтоб одна делилась на 7 без остатка, а другая - на 13 без остатка.
Задачи для самостоятельного решения
-
Решите уравнение, составленное в начале параграфа по представленным алгоритмам.
-
Решить уравнения в целых числах:
а) 27х - 40y = 1; б) 54x + 37y = 7; в) 107x + 84y =1;
г) 13x - 15y =7; д) 81x + 52y = 5; e) 24x - 56y = 72;
ж) 127x - 52y + 1 = 0; з) 6x + 10y - 7z = 11.
-
На какое наименьшее число надо умножить 7, чтобы произведение оканчивалось на 123.
-
Найти все четырёхзначные простые числа, начинающиеся и оканчивающиеся цифрой 1.
-
Кусок проволоки длиной 102 см нужно разрезать на части длиной 15 см и 12 см, так чтобы была использована вся проволока. Как это сделать? Решить уравнение в целых числах:
|
2. |
27х - 40у = 1 |
|
|
3. |
54х + 37у = 1 |
|
|
4. |
107х + 84у = 1 |
|
|
5. |
13х - 15у = 7 |
|
|
6. |
42х + 34у = 5 |
уравнение целых решений не имеет |
|
7. |
81х + 52у = 5 |
|
|
8. |
24х - 56у = 72 |
|
3. Подведение итогов урока.
Ученикам сообщается, что окончательные результаты работы будут объявлены на следующем занятии.
Выясняется мнение учеников о проведенной зачетной работе.
4. Постановка домашнего задания.
На следующем занятии - конференция по подведению итогов изучения курса. Класс делится на группы по 5-6 человек. Задача каждой группы подготовить выступление, в котором укажут, что было интересным при изучении, что сложным; что понравилось, что нет; какие предложения могут внести по усовершенствованию курса. Каждый ученик должен представить папку с задачами.
Занятие 33-34. Конференция.
Цель: подведение итогов изучения элективного курса;
Ход занятия:
1. Организационный момент: сообщение целей и плана занятия.
2. Выступление учащихся.
2.1. Защита творческих работ по теме «Тайны мира чисел» .
-
Итальянский купец Леонардо Фибоначчи и его кролики.
-
Системы счисления.
-
Арифметика на клетчатой бумаге «Квадраты и гномоны».
-
Леонард Эйлер.
-
Угадай число. Занимательные задачи.
-
О больших числах.
-
Методы решения диофантовых уравнений
-
Роль Диофанта в развитии математики.
-
Архимед - величайший древнегреческий математик, физик, инженер.
-
Математика в Древней Руси.
-
Жизнь и деятельность Пифагора.
-
Жизнь и деятельность Евклида.
2.2. Представители от каждой группы рассказывают о составленной в ходе изучения курса папки с задачами, выделяют наиболее интересные темы и задачи, наиболее трудные и легкие для усвоения.
2.3. Каждая группа отмечает «плюсы» и «минусы» данного курса, вносит свои предложения по его изучению.
3. Выступление учителя.
Учитель обобщает все сказанное учениками.
Подводит итоги по табелям баллов: сообщает уровень, на котором ученики освоили данный курс: 1 уровень - более 71 балла; 2 уровень - 41-70 баллов; 3 уровень - менее 40 баллов.
4. Подведение итогов. Вручение ученикам сертификатов, подтверждающих прохождение курса, с отмеченным в нем уровнем освоения курса.
Заключение.
Системы элективных курсов позволяют обучать персонифицировано, используя интеграцию инновационных технологий в педагогические методы, следствием чего является возможность в короткие сроки ввести слушателей в курс дела по необходимой области знаний.
Целями данной работы ставились рассмотрение положений по созданию элективных курсов и разработка элективного курса для 9 класса «Теория чисел».
В первой главе рассматривались основные положения по созданию элективных курсов. В частности, разобраны такие вопросы, как типы курсов, мотивы выбора, требования к содержанию, учебно-методический комплекс.
Во второй главе разработана методика преподавания элективного курса «Теория чисел»: представлено подробное описание каждого занятия с применяемыми методами и формами обучения, с примерами заданий, возможными формами контроля усвоения материала школьниками.
При выполнении работы было изучено и проанализировано большое количество научно - популярной и учебной литературы по указанной теме, в том числе и примеры решений уравнений в целых числах из Межрегиональной заочной математической олимпиады для школьников (Всероссийская школа математики и физики «Авангард»), из математических олимпиад Республики Мордовия, из Единого государственного экзамена (задания С6).
Данный элективный курс может иметь свое продолжение в старшей школе при изучении такого курса, как «Теория чисел».
Таким образом, цель данной работы достигнута, сформулированная гипотеза доказана.
На наш взгляд, элективные курсы незаменимы для достижения основных целей образования на старшей ступени школы. Этот материал может быть интересен и полезен учащимся, материал данной работы можно использовать для изучения на элективных занятиях, при подготовке к олимпиадам и к централизованному тестированию, а также для самостоятельного изучения.