- Учителю
- Проект 'Реализация требований ФГОС ООО при обучении учащихся 8 класса по теме 'Четырехугольники
Проект 'Реализация требований ФГОС ООО при обучении учащихся 8 класса по теме 'Четырехугольники














 ГБОУ ВПО «Академия социального управления»
ГБОУ ВПО «Академия социального управления»
Дополнительное профессиональное образование
кафедра математических дисциплин
ПРОЕКТ
Реализация требований ФГОС ООО при обучении учащихся 8 класса
теме: «Четырехугольники»
Выполнил
слушатель учебного курса
«Актуальные проблемы развития профессиональной компетентности учителя математики (в условиях реализации ФГОС)»
учитель математики МБОУ
Майская СОШ Пушкинского р-на
Романова Лилия Сергеевна
Руководитель курса: кандидат педагогических наук, доцент кафедры математических дисциплин
Фирстова Наталья Игоревна
Москва 2013
СОДЕРЖАНИЕ
Стр.
ВВЕДЕНИЕ
3
ГЛАВА 1. Теоретические основы обучения теме «Четырехугольники»
§1. Эссе «Концепция духовно-нравственного развития и воспитания личности гражданина России» …………………………………………...
5
§2. Логико-дидактический анализ содержания темы «Четырехугольники» …………………………………………………………………...
7
§3. Цели обучения теме «Четырехугольники» …………………………
16
ГЛАВА 2. Организация обучения теме «Четырехугольники»
§4. Карта изучения темы «Четырехугольники» и ее использование ….
19
§5. Учебный план темы «Четырехугольники» …………………………..
23
§6. Примеры реализации целей обучения теме «Четырехугольники» …
27
ЗАКЛЮЧЕНИЕ ……………………………………………………………
43
Список литературы ………………………………………………………..
44
ВВЕДЕНИЕ
Современный этап развития школьного математического образования характеризуется сменой предметно-ориентированной парадигмы на личностно-ориентированную, что требует адекватной разработки содержательного и процессуального компонентов образования с упором на развитие и саморазвитие учащегося, формирования личностно значимых для него знаний и способов деятельности. В этих условиях формирование только предметных математических знаний недостаточно для становления образованной личности. Наряду с предметными знаниями сегодня нужно формировать умение ориентироваться в потоке новой информации, разрешать возникающие в учебных ситуациях проблемы, отходить от стандартных способов решения задач путем переструктуирования их в соответствии с исходными условиями.
Результаты международных и массовых отечественных исследований уровня математической подготовки учащихся показывают на фоне хорошей теоретической подготовки знаний российских школьников возникновение у них трудностей, а порой полной беспомощности в нестандартных учебных ситуациях, отличающихся от привычных - тех, которые присутствовали в обучении.
Преодоление негативной стороны сложившейся ситуации школьного материала возможно посредством обращения к смысловой стороне математического содержания, к вопросу организации понимающего усвоения математики.
Цель проекта: реализация требований ФГОС ООО при изучении темы «Четырехугольники». Для достижения поставленной цели необходимо решение следующих задач:
1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС ООО.
2. Провести анализ учебной, методической математической литературы по теме исследования.
3. Провести анализ психолого-педагогической литературы, так как создаю проект для 8 класса (ученикам 13-14 лет)
4. Выполнить логико-дидактический анализ по выбранной теме.
5. Разработать тематическое планирование, таблицу целей и карту обучения теме с учетом ФГОС.
6. Разработать фрагменты конспектов уроков по выбранной теме.
7. Выполнить отбор средств обучения теме, в том числе средства ИКТ.
Решение поставленных задач потребовало использования следующих методов исследования: изучение «Концепции духовно-нравственного развития и воспитания личности гражданина России»; анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по математике; беседы с учителями, тестирование учащихся, проведение опытной проверки.
На наш взгляд, когда тема будет таким образом разработана, ученики лучше усвоят эту тему.
Изучение математики в основной школе направлено на достижение следующих целей:
-
развитие логического и критического мышления, культуры речи;
-
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
-
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни.
Цель содержания раздела «Геометрия» развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера.
Тема «Четырехугольники» имеет важное значение для всего курса математики, так как в ней рассматриваются свойства и признаки четырехугольников. Изучение сопровождается решением большого количества задач, поэтому при изучении данной продолжается развитие пространственных представлений учащихся, конструктивных навыков изображения фигур на плоскости, навыков выполнения рисунков, их правильного восприятия и чтения. Использование в задачах в многогранниках (призмы и пирамиды) позволяет подготовить учащихся к изучению соответствующего раздела в курсе стереометрии.
ГЛАВА 1. Теоретические основы обучения теме «Четырехугольники»
§1. Эссе «Концепция духовно-нравственного развития и воспитания личности гражданина России»
Считаем, что в настоящее время духовно-нравственное воспитание особенно актуально, так как в современной жизни низкий уровень общественной морали, утрачиваются семейные ценности, патриотические чувства, среди подростков процветает курение, наркомания. Поэтому на духовно-нравственное воспитание надо уделять большое внимание не только в воспитательной работе, но и на каждом уроке, в том числе и математике. Духовно-нравственное воспитание формирует у человека:
- нравственные чувства (совесть, долг, ответственность, гражданственность, патриотизм);
- нравственный облик (терпение, милосердие, кротость, незлобивость);
- нравственную позицию (способность к различению добра и зла, проявление самоотверженной любви, готовность к преодолению жизненных испытаний)
- нравственное здоровье (создание условий для сохранения физического, психического здоровья,
- воспитание негативного отношения к вредным привычкам, пропаганда физической культуры и здорового образа жизни);
- нравственное поведение (готовность служения людям и Отечеству, проявление духовной рассудительности, послушания, доброй воли).
Учитель должен помнить, что встречаясь даже с очень одаренным учеником, он готовит из него не математика, а прежде всего всесторонне развитую личность, и эту работу он выполняет в тесном единстве с учителями других школьных дисциплин. Обучение математике призвано содействовать выработке представлений о предмете математики, ее сущности и специфике её метода, расширению и обогащению жизненного опыта человека. Воспитательная функция математики осуществляется не столько благодаря её содержанию, сколько за счет использования связанного с этим содержанием обширного материала, который расширяет жизненный опыт, формирует мировоззрение и убеждения учащихся.
Мы считаем, что математика обладает большим воспитательным потенциалом. Реализация воспитательного потенциала урока математики возможна через отбор содержания материала, через структуру урока, организацию общения.
Ни один школьный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности. Даже выполнение скучных и рутинных преобразований опосредованно способствует выработке таких качеств, как собранность и систематичность.
Математика учит строить и оптимизировать деятельность, вырабатывать и принимать решения, проверять действия, исправлять ошибки, различать аргументированные и бездоказательные утверждения, Решение задач требует от учащихся добросовестной и серьезной работы над приобретением и укреплением знаний, что приводит к систематическому напряжению умственных усилий, настойчивости в преодолении трудностей. При этом у учащегося воспитываются такие черты характера как трудолюбие, усидчивость, упорство в преследовании намеченной цели, умение не останавливаться перед трудностями и не впадать в уныние при неудачах.
Перед современным обучением математике поставлен комплекс взаимосвязанных целей - образовательных, развивающих, воспитательных. Обучение математике требует от школьников умственных и волевых усилий, развитого внимания и отточенного логического мышления, воспитание таких качеств, как активность, творческая инициатива, умений коллективного учебно-познавательного труда.
Заканчивая, хочется обратиться к словам замечательного С.Л. Соловейчика, который в своей книге «Педагогика для всех» говорит: «Воспитание - это обучение нравственной жизни, т.е. обучение нравственным средствам. Воспитывая детей, мы учим их добиваться своих целей за свой счет - пользуясь лишь нравственными средствами. Нравственность (определяемая вопросом «за чей счет?») указывает нижнюю границу возможных для человека действий и поступков; через требования нравственности переступить невозможно. Нравственность - граница дозволяемого совестью. А верхней границы нет, вверх - духовность, она бесконечна... Будет нравственность, почти наверняка будет и духовность; не будет нравственности - не будет ничего, никакого воспитания». [16]
§2. Логико-дидактический анализ темы «Четырехугольники»
Хоть я не особенно забочусь о славе, однако параллелограммом горжусь больше, чем каким-либо другим изобретением, сделанным мною.
Джеймс Уатт
(английский изобретатель, 1736-1819)
Основная цель изучения темы "Четырехугольники" - изучить наиболее важные виды четырехугольников - параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией. Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников.
В древних египетских и вавилонских математических документах встречаются следующие виды четырехугольников: квадраты, прямоугольники, равнобедренные и прямоугольные трапеции. В частности, в клинописных математических табличках встречаются прямоугольные треугольники, рассеченные параллелями к одному из катетов на прямоугольные трапеции
Термин «параллелограмм» - греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцами.
В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба
Термин «диагональ» происходит от сочетания двух греческих слов «диа» (через) и «гониос» (угол), то есть прямая, проходящая через вершины углов. Однако Евклид и большинство древнегреческих математиков пользовались почти всюду, в частности для прямоугольника, не этим, а другим термином: диаметр. В средние века были в ходу оба термина. Фибоначчи и Региомонтан еще пользовались термином «диаметр». Лишь в XVIII в. термин «диагональ» входит в общее употребление.
Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Образ ромба был связан первоначально с сечением, проведенным в обмотанном веретене.
Термин «квадрат» происходит от латинского quadratum (quadrare - сделать четырехугольным), перевод с греческого «тетрагонон» - четырехугольник.
Трапеция - слово греческое означавшее в древности «столик». В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырехугольник (не параллелограмм).
Предложение о том, что средняя линия трапеции равна полусумме ее оснований, было известно древним египтянам, оно содержится в папирусе Ахмеса и фигурирует в виде инскрипции (II в. до н. э.) на стенах Эдфу в верхнем Египте. Это предложение было известно также вавилонским землемерам, оно содержится и в трудах Герона Александрийского. [3]
Изучение этой темы необходимо для изучения смежных дисциплин: в физике применяют параллелограмм при изучении разложения сил, при нахождении равнодействующей силы; в стереометрии при изучении призмы, четырехугольной пирамиды, в черчении.
Интересные факты.
С помощью снимка галактики Certaurus А, сделанным инфракрасным космическим телескопом Spitzer, впервые удалось определить структуру пылевого облака галактики. Оказалось, что оно имеет форму параллелограмма
За счёт трёхмерной оптической иллюзии в комнате Эймса (придумал в 1946 году) ребёнок в ближнем углу кажется великаном по сравнению с тем, что стоит в дальнем. На самом деле форма комнаты - трапеция. Эффект усиливается из-за искажённой шахматной клетки.

Символы индейцев Северной Америки
Квадрат выражает постоянство, стойкость и надежность. Он дает защиту. Все стоит на стабильной основе.
Ромб символизирует защитную силу ветра. Он изображает четыре фазы учения, показывает, что смысл жизни в равенстве, единстве и в свободе от страхов.
Прямоугольник указывает на концентрацию на чем-то одном. Применительно к человеку знак сообщает, что тот работает или действует лучше всего в одиночку.
Параллелограмм олицетворяет благодарность, способность учиться и принимать новые идеи.
Свойство подвижности параллелограмма часто используется на практике. Так, шарнирный параллелограмм применяется, например, для проведения параллельных прямых на различных расстояниях друг от друга.
Ромб, в котором проведены диагонали, считается одной из самых крепких и
выносливых конструкций. Такую конструкцию очень широко используют для постройки мостов, зданий, и даже, для рамы мотоцикла.
Ученики с некоторыми понятиями были ознакомлены ранее в начальной школе и в 5 классе, но определения не вводились.
Тема «четырехугольники» изучается в начале восьмого класса. На её изучение отводится целая глава. Первый параграф данной главы посвящен многоугольникам. Дается определение многоугольника (п. 39), а также что называют вершинами и сторонами многоугольника. Говорится, что называется n-угольником. Приводятся примеры фигур, которые являются многоугольниками и тех, которые не являются многоугольниками. Дается определение соседних вершин и диагоналей многоугольника. В конце данного пункта говорит о том, что любой многоугольник разделяет плоскость на две части (внутренняя и внешняя область многоугольника).
В следующем пункте первого параграфа (п. 40) рассказывается о выпуклых многоугольниках. Приводится пример выпуклого и невыпуклого многоугольника. Рассматривая выпуклый n-угольником A1A2A3…An-1An говорится, что углы AnA1A2, A1A2A3, …, An-1AnA1 называются углами этого многоугольника и показывает чему равняется сумма углов выпуклого n-угольника.
Последний пункт данного параграфа (п. 41) посвящен четырехугольнику. Определение четырехугольника не дается, просто говорится, что четырехугольник имеет четыре вершины, четыре стороны и две диагонали. Дается определение противоположных сторон и вершин. Приводится пример выпуклого и невыпуклого четырехугольника. На основании суммы углов выпуклого n-угольника делается вывод, что сумма углов выпуклого четырехугольника равна 360°.
Второй параграф посвящен параллелограмму и трапеции. При изучении параллелограмма (п. 42) дается его определение, и доказываются его свойства.
В следующем пункте параграфа (п. 43) рассказывается о признаках параллелограмма. Рассматривается три признака параллелограмма. Это позволяет быстрее решать задачи на доказательство.
Последний пункт параграфа (п. 44) отводится трапеции. В этом пункте дается определение трапеции и рассматриваются виды трапеции. В этом учебнике также предлагается для изучения теорема Фалеса, но в явном виде она не выделена отдельным пунктом.
Третий параграф посвящен прямоугольнику, ромбу и квадрату. Определение прямоугольника и ромба даются на основе параллелограмма. Так как прямоугольник и ромб являются параллелограммом, то они обладают всеми свойствами параллелограмма. Также в учебнике рассматривается особые свойства прямоугольника и ромба. Определение квадрата дается на основе прямоугольника. Так же говорится, что квадрат является ромбом, так как стороны квадрата равны. На основе этого делается вывод, что квадрат обладает свойствами прямоугольника и ромба, добавляются особые свойства квадрата.
В конце параграфа отдельным пунктом (п. 47) выделена осевая и центральная симметрия. В конце главы предлагаются задачи на отработку ЗУН.
Изучение четырехугольников в учебнике Л. С. Атанасяна идет по следующей схеме:
Параллелограмм → Трапеция → Прямоугольник → Ромб → Квадрат
В учебнике четырехугольник вводится как частный вид многоугольника.
Структурно - логическая схема имеет вид:
Многоугольник
невыпуклый
Выпуклый
Четырехугольники
Треугольник
Трапеция
Параллелограмм
Равнобедренная
Прямоугольная
Прямоугольник
Ромб
Квадрат
При классификации всех четырехугольников за основание классификации принимается сначала взаимное расположение противоположных сторон - не параллельность или параллельность их, вследствие чего множество всех выпуклых четырехугольников разбивается на три класса:
-
четырехугольники, не имеющие параллельных сторон;
-
трапеции (одна пара параллельных сторон);
-
параллелограммы (две пары параллельных сторон).
За основание классификации параллелограммов принимается равенство или неравенство смежных сторон (собственно параллелограммы и ромбы), а также отсутствие или наличие прямого угла (собственно параллелограммы и прямоугольники).
В основу классификации ромбов кладется отсутствие или наличие прямого угла (собственно ромбы и квадраты).
При классификации прямоугольников за основание принимается равенство или неравенство смежных сторон (собственно прямоугольники и квадраты).
Логическая организация учебного материала происходит на дедуктивной основе, аксиомы вводятся в начале изучения курса геометрии, в 7 классе.
Классификация трапеции проводится сначала по длине боковых сторон (равнобедренная и неравнобедренная трапеции); затем неравнобедренные трапеции в свою очередь разбиваются на прямоугольные и непрямоугольные.
Определение многоугольника. Фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а не смежные отрезки не имеют общих точек, называется многоугольником. Существенные признаки: 1) геометрическая фигура; 2) состоит из отрезков; 3) смежные отрезки не лежат на одной прямой; 4) не смежные отрезки не имеют общих точек.
Определение параллелограмма. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Определение параллелограмма дается через род и видовое отличие (род - четырехугольник, видовое отличие − противоположные стороны попарно параллельны)
Определение трапеции. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Определение трапеции через род и видовое отличие (род - четырехугольник, видовое отличие − две стороны параллельны, другие две не параллельны).
Определение прямоугольника. Прямоугольником называется параллелограмм, у которого все углы прямые. Определение прямоугольника дается через род и видовое отличие (род - параллелограмм, видовое отличие − углы прямые).
Определение ромба. Ромбом называется параллелограмм, у которого все стороны равны. Определение ромба дается через род и видовое отличие (род -параллелограмм, видовое отличие − стороны равны).
Определение квадрата. Квадратом называется прямоугольник, у которого все стороны равны. Определение квадрата дается через род и видовое отличие (род - прямоугольник, видовое отличие − стороны равны).
Первая теорема о сумме углов многоугольника словесно - символическая, категоричная. Сумма углов выпуклого п-угольника равна (п − 2)∙180°. Метод доказательства цепочка треугольников.
Свойства параллелограмма две словесные категоричные теоремы: 1) В параллелограмме противоположные стороны равны и противоположные углы равны. 2) Диагонали параллелограмма точкой пересечения делятся пополам. Метод доказательства цепочка треугольников.
Три признака параллелограмма словесные условные теоремы: 1) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм. 2) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм. 3) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм. Метод доказательства - цепочка треугольников. Еще два признака параллелограмма введены в задачах №429 (если сумма углов прилежащих к каждой из двух смежных сторон, равна 180°) и №430 (если противоположные углы четырехугольника попарно равны).
Теорема Фалеса предложена в виде решенной задачи №385
Свойства углов и диагоналей равнобедренной трапеции даны в задаче №388.
Признаки равнобедренной трапеции в задаче №389.
Свойство диагоналей прямоугольника словесная условная теорема доказывается методом цепочки треугольников. (Диагонали прямоугольника равны)
Признак прямоугольника (обратное утверждение) словесная условная теорема, доказывается методом цепочки треугольников. (Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник). Еще два признака прямоугольника в задачах №399 (Параллелограмм, один из углов которого прямой, является прямоугольником) и №400 (Если в четырехугольнике все углы прямые, то четырехугольник - прямоугольник).
Особое свойство ромба словесная категоричная теорема, доказывается аналитико-синтетическим методом (Диагонали ромба взаимно перпендикулярны и делят его углы пополам). Некоторые признаки ромба даны в задаче №408 (Параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ является биссектрисой его угла). Нет признака ромба через четырехугольник.
Для квадрата сформулированы основные свойства: 1. Все углы квадрата прямые. 2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признак квадрата через ромб сформулирован в задаче №409 и через четырехугольник неявно в №410.
Раскрытию темы способствует 33 задачи. Все задачи сгруппированы, но нет дифференциации. Внимание всего класса следует сосредоточить на задачах №374(задача о биссектрисе параллелограмма), №385(теорема Фалеса), №386(свойство отрезка, соединяющего середины сторон трапеции), №388(свойства равнобедренной трапеции) №389(признаки равнобедренной трапеции), №399, №400(признаки прямоугольника), №402, №404(свойство медианы прямоугольного треугольника, проведенной к гипотенузе), №405, №408, №409, №410(является ли четырехугольник квадратом?)
Задачи №402, №407, №374, №375 готовят к следующей контрольной работе:
Вариант 1.
1. Диагонали прямоугольника АВСD пересекаются в точке О. Найдите угол между диагоналями, если АВО=30°
2. В параллелограмме КМNР проведена биссектриса угла МКР, которая пересекает сторону МN в точке Е.
а) Докажите, что треугольник КМЕ равнобедренный;
б) Найдите сторону КР, если МЕ=10см, а периметр параллелограмма равен 52см.
Вариант 2
1. Диагонали ромба КМNР пересекаются в точке О. найдите углы треугольника КОМ, если МNР=80°.
2. На стороне ВС параллелограмма АВСD взята точка М так, что АВ = ВМ.
а) Докажите, что АМ - биссектриса ВАD.
б) Найдите периметр параллелограмма, если СD=8см, См=4см.
Классификация задач
По характеру требования задачи
По методам решения задачи
На вычисление
На доказательство
На построение
Комбинированные
Аксиоматический
Метод от противного
Алгебраичес-кий метод
364, 365, 366, 367, 368, 369, 370, 372, 373, 376, 377, 387, 390
371, 378, 379, 380, 381, 382, 383, 384, 385, 386, 388, 389, 391, 399, 400, 402, 404,408, 409, 410, 411, 419, 420
393, 394, 395 396, 397, 398
413, 414, 415, 416, 421
374, 375, 392, 401, 405, 406, 407, 412
371, 379, 380, 381, 382, 383, 384, 385, 386, 388, 389, 399, 400, 402, 404, 408, 409, 410, 411
нет
364, 365, 366, 367, 368, 369, 370, 372, 377
№393 и №410 задачи на формирование поиска решения.
Задачи, показывающие приложения изучаемых вопросов в ранее изученных темах математики в 5 классе: №№366, 367.
Занимательных задач нет. К задачам с нестандартной фабулой можно отнести задачу № 381 (прикладного характера).
Задачи прикладного содержания.
Задача 1. Деревни расположены в вершинах прямоугольника. В каком месте построить мост через реку, чтобы он был одинаково удалён от всех деревень?
Задача 2. Как, используя свойство сторон параллелограмма, измерить ширину озера?
Задача 3. Как швея убеждается в том, что кусок материи имеет форму квадрата?
Задача 4. В прямоугольной пластине нужно просверлить круглое отверстие на равном расстоянии от вершин. Как найти центр отверстия?
Исторические задачи.
Теорема Эйлера. «Во всяком четырехугольнике сумма квадратов сторон равна сумме квадратов его диагоналей, сложенной с учетверенным квадратом отрезка, соединяющего середины диагоналей».
Задача Я. Штейнера. «Если соединить точку Е пересечения диагоналей трапеции с точкой F пересечения ее непараллельных сторон, то большее ее основание разделиться пополам линией ЕF. Доказать!»
Учащиеся должны знать: определение многоугольника, формулу суммы углов выпуклого многоугольника, определение параллелограмма и его свойства, формулировки свойств и признаков параллелограмма, определение трапеции, свойства равнобедренной трапеции, формулировку теоремы Фалеса, основные типы задач на построение, определение прямоугольника, его элементы, свойства и признаки, определение ромба, квадрата как частных видов параллелограмма, виды симметрии в многоугольниках.
Уметь: распознавать на чертежах многоугольники и выпуклые многоугольники, используя определение, применять формулу суммы углов выпуклого многоугольника при нахождении элементов многоугольника, распознавать на чертежах среди четырехугольников, доказывать, что данный четырехугольник является параллелограммом, выполнять чертежи по условию задачи, находить углы и стороны параллелограмма, используя свойства углов и сторон, распознавать трапецию, ее элементы, виды на чертежах, находить углы и стороны равнобедренной трапеции, используя ее свойства, делить отрезок на n равных частей, выполнять необходимые построения, распознавать и изображать ромб, квадрат, находить стороны и углы, используя свойства, строить симметричные точки и распознать фигуры, обладающие осевой и центральной симметрией, находить в прямоугольнике угол между диагоналями, используя свойство диагоналей, углы в прямоугольной или равнобедренной трапеции, используя свойства трапеции, стороны параллелограмма, отличать свойства от признаков.
Средства обучения: ТСО, компьютер, интерактивная доска, тетради с печатной основой, рабочие тетради, «Живая математика», таблицы, модели, чертежи и рисунки
Методы обучения: объяснительно-иллюстративный, частично-поисковый, проблемный, исследовательский, самостоятельная работа учащихся.
Формы контроля и оценки. Устный опрос, контрольная работа, самостоятельная работа, коллективная, индивидуальная и фронтальная работа.
§3. Цели обучения теме «Четырехугольники»
Таблица целей обучения теме «Четырехугольники»
Формулировки обобщенных целей
Формулировки учебных задач, с помощью которых достигается обобщённая цель; цель считается достигнутой, если ученик на уровнях:
Опознаваемость
целей
первом
втором
третьем
Ц 1: приобретение учебной информации и становление интеллектуальных умений при изучении: а) понятий многоугольника и его частного вида четырехугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; б) свойств и признаков всех видов четырехугольников; в) задач типа
Ц 1: а) составляет схему определения понятия многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата с использованием учеб-ника и набора объектов; б) создаёт знаковую модель теорем свойств и признаков видов четырехугольников с использованием учебника, карточек с пропусками; в) сравнивает решение однотипных задач 1-го уровня сложности, классифицирует эти задачи, используя помощь.
Ц 1: а) самостоятельно составляет схему определения понятия четырехугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата с использованием набора объектов взаимосвязи понятий, изученных в теме; б) ищет доказательство с помощью схемы поиска; составляет план доказательства; выделяет базис доказательства; в) обобщает решение задач одного типа, составляет приёмы их решения с помощью подсказки.
Ц 1: а) исследует располо-жение указанных объектов, самостоятельно составляет схему определения понятия четырехугольника, парал-лелограмма, трапеции, пря-моугольника, ромба, квад-рата; б) доказывает теоремы, самостоятельно или с помощью неполной схемы поиска; составляет блок-схему доказательства теоремы; в) систематизирует задачи по уровню сложности.
Ц1: а) приёмы составления схемы понятия, блок-схем; б) общие приёмы поиска доказательства утвержде-ний; в) карточки - информаторы различного уровня
Ц 2: контроль усвоения теоретических знаний при работе: а) с геометрическими понятиями; б) с теоремами; в) с типами и классами задач
Ц 2: а) воспроизводит схему определения понятия и формулирует определение многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; приводит примеры; перечисляет признаки; выбирает из данных формулировок определение; вставляет пропущенные в определении слова; умеет выделять существенные признаки понятия; подводит объект под понятие; б) формулирует теорему; заполняет пропуски в доказательстве, используя готовую схему; умеет выполнять действия выведения следствий на основании данных задач и требований; в) использует предписания для решения задач первого уровня
Ц 2: а) формулирует опре-деление понятия многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; подводит объект под понятие; приводит контрпримеры; выводит следствия из условия принадлежности объекта данному понятию; воспроизводит классификацию понятий; б) выполняет доказательство на своей модели; заполняет пустую готовую схему доказательства; называет базис доказательства; воспроизводит план доказательства; в) использует предписания для решения типов задач второго уровня
Ц 2: а) формулирует определение понятия многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; устанавливает связи данного понятия с ранее изученными; различает свойства и признаки понятия; указывает область применения данного понятия; воспроизводит предписания по распознаванию; составляет полный набор объектов для подведения под понятие; и др. б) описывает основную идею доказательства; указывает область применения теоремы; описывает способы рассуждений на этапах «открытия», поиска доказательства теоремы; в) решает задачи рассмотренных классов уровня 3
Ц 2: схемы решения задач всех типов, рассматриваемых в теме
Ц 3: применение знаний и интеллектуальных умений при решении геометрических и учебных задач
Ц 3: решает задачи своего уровня сложности, составляет задачи: по готовому чертежу и требованию, по неполному условию и требованию, по условию без требования; аналогичные, обратные задачи и решает, используя помощь
Ц 3: а) учебник; словарь, схемы определения понятий, алгоритм распознавания, классификации; б) схема доказательства теоремы; образец записи доказательства теоремы; в) образцы записей решений задач в учебнике и тетради
Ц 4: формирование коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
Ц 4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
Ц 4: приемы контроля усвоения понятия, доказательства теоремы, решения задачи; рецензирования;
Ц 5: формирование организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД)
Ц 5: а) формулирует цели своей учебной деятельности; б) выбирает задачи и решает их, в) осуществляет самопроверку с использованием образцов, приёмов; г) составляет контрольную работу для своего уровня усвоения; д) оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; е) делает выводы о дальнейших действиях, планирует коррекцию учебной познавательной деятельности (УПД)
Ц 5: приёмы выбора и рефлексии достижения целей; диагностики и коррекции собственной УПД
§4. Карта изучения темы «Четырехугольники»
I. Последовательность уроков и цели изучения темы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Ц 1, Ц 5
Ц 1 -
Ц 3
Ц 2 Ц -4
Ц 1, Ц 2
Ц 2 - 4
Ц 2 -4
Ц 1-3
Ц2 - 4
Ц 2 - 5
Ц 1
Ц 2 - 4
Ц2 - 4
Ц 1
Ц 2-4
Ц 2 - 4
Ц 2 - 5
п. 39-41
п. 39-41
п. 42,43
п. 42, 43
п. 42,43
п. 44
п. 44
п. 44
п. 45
п. 45
п. 46
п. 46
Подг. к КР
Контрольная работа
Урок
коррекции
II. Блок актуализации знаний учащихся
Знать: определение многоугольника, формулу суммы углов выпуклого мн-ка, определение параллелограмма, трапеции, прямоугольника, ромба, квадрата, их свойства и признаки, формулировку теоремы Фалеса, виды симметрии в многоугольниках
Уметь: распознавать на чертежах многоугольники и выпуклые многоугольники, применять формулу суммы углов многоугольника, распознавать на чертежах среди четырехугольников, доказывать, что данный четырехугольник является параллелограммом, находить углы и стороны параллелограмма, используя св-ва углов и сторон, находить углы и стороны равнобедренной трапеции распознавать и изображать ромб, квадрат, находить стороны и углы, используя свойства, строить симметричные точки и распознать фигуры, обладающие осевой и центральной симметрией, находить в прямоугольнике угол между диагоналями, используя свойство диагоналей, отличать свойства от признаков.
III. Предметные результаты (Ц 2, 3 таблицы целей): формулировать определение понятия многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; подводить объект под понятие; выводить следствия из условия принадлежности объекта данному понятию; воспроизводить классификацию понятий; доказывать свойства и признаки видов четырехугольников; решать задачи на вычисление, доказательство и построение.
VI. Образцы заданий, аналогичных заданиям итоговой контрольной работы (Ц 2, Ц 3, Ц 5)
V. Средства обучения теме
1 уровень
Баллы
2 уровень
Бал-лы
3 уровень
Баллы
1. Диагонали прямоугольника МNКР пересекаются в точке О, МОN=64°. Найдите угол ОМР.
2. Найдите углы равнобедренной трапеции, если один из его углов на 30° больше второго.
3. Стороны параллелограмма относятся как 3:1, а его периметр равен 40 см. Найдите стороны параллелограмма.
1
1
1
1. Периметр параллелограмма равен 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.
2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4:5.
3. В трапеции АВСD диагональ ВD перпендикулярна боковой стороне АВ, АDВ=ВDС=30°. Найдите длину АD, если периметр трапеции 60 см.
1
1
2
1. В равнобокой трапеции длина боковой стороны 2d, длины оснований 5d и 7d. найдите углы трапеции.
2. В параллелограмме АВСD известно, что А=60°, АВ=10, АD=16. Найдите расстояние от вершин В и D до биссектрисы ВСD.
3. Внутри квадрата АВСD выбрана точка М так, что треугольник АМD равносторонний. Найдите угол АМВ.
1
2
2
-
Таблицы
-
Чертежи
-
Схемы
-
Предписания
-
Карточки с приемами решения задач
-
Приёмы саморегуляции
VI. Задания для домашней работы (Ц 2, 3, 5)
1 уровень (обязательный уровень стандарта): №№ 363, 364, 365, 370, 371, 372, 376, 387, 392, 399, 400, 401, 402, 403, 405, 407, 409, 416, 417, 421, 422
2 уровень: №№ 373, 377, 379, 388, 396, 404, 408, 410, 411, 412, 413, 414.
3 уровень: №№ 378, 384, 393, 394, 397, 398, 413
4 уровень: №№ (со звёздочкой) нет в учебнике
VII. Темы индивидуальных заданий (Ц 5)
1) В мире четырехугольников. 2) Симметрия на плоскости . 3) Задачи на построение. 4) Удивительный квадрат. 5) Решение задач с помощью центральной и осевой симметрии. 6) Паркеты из многоугольников. 7) Самостоятельно выбранная тема.
Список литературы:
-
Болтянский В.Г. Геометрические преобразования плоскости /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. - М.: Просвещение, 1991.
-
Болтянский В.Г. Движения плоскости / Школа в Кванте. Геометрия / Под редакцией А.А.Егорова. - М.: Бюро Квантум, 1995 (Приложение к журналу «Квант» - 1995. - № 1).
-
Болтянский В.Г. Паркет из четырехугольников //Квант. - 1989. - № 11.
-
Гейдман Б. Осевая симметрия //Приложение к журналу «Квант» № 1/1995. - М.: Бюро «Квантум», 1995.
-
Гончарова С.Г., Кукин Г.П. Конструктор «В мире симметрии» //Математика в школе. - 1996. - № 3.
-
Готман Э.Г. Задачи по планиметрии и методы их решения. - М.: Просвещение, 1996.
-
Заславский А. Паркеты и разрезания //Квант. - 1999. - № 2.
-
Зеркальная симметрия //Квант. - 1992. - № 3.
-
Квадрат //Квант. - 1989. - № 5.
-
Кордемский Б.А., Русалев Н.В. Удивительный квадрат. - М.: Столетие, 1994.
-
Лоповок Л.М. Тысяча проблемных задач по математике: Книга для учащихся. - М.: Просвещение, 1995.
-
Прасолов В.В. Задачи по планиметрии. Часть I. - 2-е изд. - М.: Наука, 1991.
-
Семенов Е.Е. За страницами учебника геометрии. - 2-е изд. - М.: Просвещение, 1999, с. 143.
-
Сергеев И.Н. и др. Примени математику. - М.: Наука, 1989.
-
Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995.
-
Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. - М.: Мнемозина, 2005.
-
Тарасов Л.В. Этот удивительно симметричный мир. - М.: Просвещение, 1982.
-
Энциклопедия для детей. Математика. Том 11. - М.: Аванта, 2001.
VIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1 - 5)
Познавательные УУД
Регулятивные УУД
Коммуникативные УУД
Личностные УУД
Сравнение, обобщение, конкретизация, анализ;
составление схемы определения понятия, подведение под понятие;
постановка и решение проблемы при составлении задачи
Выбор и принятие целей, составление плана, самоконтроль, самооценка, соотнесение своих знаний с той учебной информацией, которую нужно усвоить;
приёмы саморегуляции
Взаимоконтроль, взаимопроверка, распределение обязанностей в группе, умение слушать, выступать, рецензировать, писать текст выступлений
Рефлексия собственной деятельности
§5. Тематическое и почасовое планирование образовательных результатов освоения математики
на 2013/2014 учебный год (фрагмент)
Класс: 8
Учитель: Романова Л.С.
Количество часов: на учебный год: 85 в неделю: 2/3
Плановых контрольных уроков: I ч. - 1; II ч. - 1; III ч. - 2; IV ч. - 2;
Планирование составлено на основе источников:
1) Примерное тематическое планирование к учебнику геометрия 7-9
2) Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. Геометрия, 7-9 классы: учеб. для общеобразоват. учреждений. М.: Просвещение, 2010
3) Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Некрасов В.Б., Юдина И.И. Изучение геометрии в 7-9 класса: Методические рекомендации к учебнику. Книга для учителя. М.: Дрофа,2003
5) Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 8 класса. М.: Просвещение, 2004
6) Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. М.: ИЛЕКСА, 2010
7) Рабинович Е.М. Задачи и упражнения на готовых чертежах. Москва-Харьков: ИЛЕКСА, 1998
Тематическое планирование составил: Дата 2013 Роспись _____________
Условные обозначения: ПУУД - познавательные УУД; ПЛ УУД - познавательные логические УУД; ПО УУД - познавательные общеучебные УУД; РУУД - регулятивные УУД; КсУУД - коммуникативные УУД сотрудничество; КрУУД - коммуникативные УУД для общения: развитие устной и письменной речи; Ц1 - Ц 5 - цель 1 - 5; ДЗ - домашнее задание; УПД - учебно-познавательная деятельность.
№ уро-
ков
Раздел, тема урока
Форма урока; форма обучения
Предметные и метапредметные результаты
Ц 1 (ПЛ УУД), Ц 2 (ПО УУД, РУУД), Ц 3 , Ц 4 (КсУУД, КРУУД), Ц 5 (ПОУУД, РУУД)
1 - 15
Название темы
Четырехугольники
Средства обучения
1) таблицы, модели
2) подсказки к поиску решения задач;
4) карточки с приёмами;
5) Карта темы
Уроки: смешанного типа, семинар, практикум, лекция.
Фронтальная, индивидуальная,
групповая
формы обучения
Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий; б) теорем; в) типов задач
Ц 2: контроль усвоения теоретических знаний: а) математических понятий; б) теорем; в) типов и классов задач
Ц 3: применение знаний и интеллектуальных умений при решении математических и учебных задач
Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
Ц 5: развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД
1
Многоугольники
п. 39 41
Инструктивная лекция (целеполагание, освоение новой учебной информации)
Фронтально-индивидуальная
Ц 5: Введение в тему, постановка и формулирование целей своей учебной деятельности;
Ц 1: Развитие познавательных логических УУД
2
Многоугольники
п. 39 41
Урок смешанного типа
Фронтально-индивидуальная
Ц 2
Ц 3
Ц 4
3
Параллелограмм
п. 42
Урок смешанного типа (целеполагание, освоение новой учебной информации)
Фронтальная
Ц 1, Ц 3, Ц 4, Ц 5
4
Параллелограмм
п. 43
Урок смешанного типа (освоение новой учебной информации)
Фронтально
Постановка и решение проблемы (познавательные УУД)
Ц 1: составление плана и поиска доказательства, составление предписаний;
Ц 2: контроль усвоения изученного материала в процессе чтения лекции
5
Параллелограмм
п. 42, 43
Урок смешанного типа
Ц 2: находит ошибки в решении задач своего уровня сложности; решает задачи своего уровня сложности;
Ц 4:
6
Трапеция
п. 44
Урок смешанного типа
Ц 2, 3
Ц 4: в соответствии таблицей целей;
Ц 5
7
Трапеция
п. 44
Урок смешанного типа
Ц 1 - 3 Развитие познавательных логических УУД
8
Трапеция
п. 44
Практикум
Ц 2 - 4 Развитие познавательных, общеучебных, регулятивных УУД
9
Прямоугольник
п. 45
Урок смешанного типа (целеполагание, освоение новой учебной информации)
Ц 5, Ц 1 приобретение учебной информации при изучении свойств и признаков прямоугольника
Развитие познавательных логических УУД
10
Прямоугольник
п. 45
Урок смешанного типа
Ц 2 - 4 : использует предписания для решения типов задач своего уровня сложности.
11
Ромб. Квадрат
п. 46
Урок смешанного типа
Ц 5, Ц 1. Развитие познавательных логических УУД
12
Осевая и центральная симметрия
п. 47
Вводный обзорный семинар
Групповая работа
Ц 5, Ц 1. Развитие познавательных логических УУД
13
Решение задач по теме «Четырехугольники»
Урок решения задач. Подготовка к котрольной работе.
Ц 5: делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы
14
Контрольная работа №1 по теме «Четырехугольники»
Практикум.
Индивидуальная
Ц 2, 3, 5: выбирает задачи своего уровня сложности, решает их, осуществляет самопроверку; делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы
15
Урок коррекции и рефлексии
Рефлексивный семинар
Индивидуальная, парная (взаимопомощь)
Ц 2, Ц 4: анализирует собственные ошибки с помощью товарища и исправляет их;
Ц 5: ( в соответствии с таблицей целей): вспоминает планируемые цели своей учебной деятельности; е) делает выводы о результатах своей деятельности; планирует коррекцию учебной познавательной деятельности
Внеурочная самостоятельная деятельность:
I. Тематика для подготовки рефератов, выступлений на конференции (по итогам изучения темы): 1) В мире четырехугольников. 2) Удивительный квадрат. 3) Паркеты из многоугольников. 4) Симметрия на плоскости. 5) Самостоятельно выбранная тема.
II. Тематика долгосрочных проектов по разделу
1) Решение задач с помощью дополнительных построений. 2) Решение задач с помощью центральной и осевой симметрии.
§6. Примеры реализации целей обучения теме «Четырехугольники»
Технологическая карта урока
Предмет, класс
Геометрия 8 класс
Автор (ы) УМК
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
ФИО учителя, школа
Романова Лилия Сергеевна,
Учитель математики МБОУ Майская СОШ Пушкинского муниципального района
Тема урока
Параллелограмм
Тип урока
Урок освоения новой учебной информации
Деятельность учителя
Деятельность учащихся
(осуществляется через действия)
3. УУД (название, вид)
ЭТАП 0. Организационный момент
Проверка готовности обучающихся к уроку (наличие учебных принадлежностей)
Обучающиеся проверяют свою готовность к уроку.
Записывают число в тетрадях.
ЭТАП I. Повторение необходимых знаний
Проверка домашнего задания, используя слайды презентации.
Учитель проводит опрос по теории. Предлагает решение задач на готовых чертежах
Проверяют правильность выполнения домашнего задания.
Отвечают на вопросы
Решают устно задачи
1.1.3, 1.1.6
ЭТАП II. Мотивация к учебной деятельности и постановка целей урока
Нацеливает на систематизацию материала и применение умений к решению задач. Подводит учащихся к формулированию цели и задач урока
Учащиеся отвечают на вопросы. Под руководством учителя выделяют тему урока и формулируют познавательную цель урока.
1.1.0, 1.1.1, 1.1.6, 1.1.7
ЭТАП III. Создание проблемной ситуации и формулирование проблемы
предлагая решить задачу на слайде презентации
Решают задачу. Обсуждают полученный результат.
1.3.1, 1.3.2, 1.3.3
ЭТАП IV. Выдвижение гипотез, составление плана действий для решения проблемы, её решение (создание эталона)
Предлагает сверить свои выводы и догадки в учебнике
Самостоятельно формулируют определение параллелограмма. Работают в парах. Проверяют себя по учебнику
1.1.2, 1.1.3, 1.2.2, 1.3.2
ЭТАП V. Первичное закрепление (действие в форме громкой, внешней речи)
Использует типовые задачи
Решают задачи, выделяют признаки объекта.
Синтезируют знания.
1.1.4, 1.2.3, 1.2.4, 1.2.5, 1.2.8, 1.2.9, 2.2.1
ЭТАП VI. Рефлексия деятельности (соотнесение результатов с поставленными целями урока)
Предлагает сделать анализ своей работы на уроке. Задает вопросы.
Обсуждают свою работу на уроке, высказывают свое мнение о своих достижениях на уроке.
1.1.6, 1.1.7, 1.1.8, 2.2.1, 2.2.2
Конспект фрагмента урока по геометрии в 8 классе
Предмет: геометрия, класс: 8, авторы учебника: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
Тема урока: Параллелограмм (п. 42).
Всего часов на тему: 3
Номер урока в теме: 1
Тип урока: урок изучения нового материала
Цели урока:
-
Образовательные: ввести понятие параллелограмм, его элементов;
-
Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
-
Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.
-
Планируемые образовательные результаты
-
Предметные
-
Метапредметные результаты (УУД)
-
Личностные
Регулятивные
Познавательные
Коммуникативные
Знать: определение параллелограмма
Уметь: различать на чертеже среди четырехугольников доказывать, что данный четырехугольник является параллелограммом
1.1. принимать учебную задачу; 1.2. планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану; 1.3. контролировать процесс и результаты деятельности, вносить необходимые коррективы; 1.4. адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления.
2.1. осознавать познавательную задачу; 2.2. читать и слушать, извлекая нужную информацию, понимать информацию, выполнять УУД; 2.3. осуществлять для решения учебных задач операции анализа, синтеза, сравнения; 2.4. устанавливать причинно-следственные связи, делать выводы.
3.1. вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения; 3.2. задавать вопросы, слушать и отвечать на вопросы других, формулировать собственные мысли, высказывать и обосновывать свою точку зрения; 3.3. строить небольшие монологические высказывания; 3.4. осуществлять совместную деятельность в парах и рабочих группах с учётом конкретных учебно-познавательных задач.
4.1. положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся; 4.2. осознавать свои трудности и стремиться к их преодолению; 4.3. осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
Организационная структура урока
Этапы урока
Задачи этапа
Деятельность учителя
Деятельность учащихся
Средства: учебник, интерактивная доска
Организационный момент
УУД:4.1
Вхождение в тему урока и создание условий для осознанного восприятия нового материала
УУД: 1.3, 1.4, 2.2, 3.1-3.3, 4.1, 4.2.
Повторение опорных знаний.
Фронтальный опрос:
-
Какая фигура называется четырехугольником?
-
Какие вершины четырехугольника называются соседними, какие противолежащими?
-
Что такое диагонали четырехугольника?
-
Какие стороны четырехугольника называются соседними? Какие стороны называются противолежащими?
-
Какие углы образуются при пересечении двух прямых секущей
Предлагает решение задач на готовых чертежах
Необходимо вспомнить следующие темы: признаки параллельных прямых
Необходимо вспомнить следующие умения: доказывать параллельность прямых
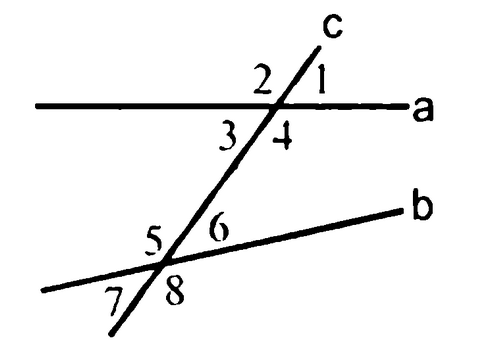

УУД: 1.1, 2.1, 2.2-2.4,3.1-3.3, 4.1
Мотивация учебной деятельности.
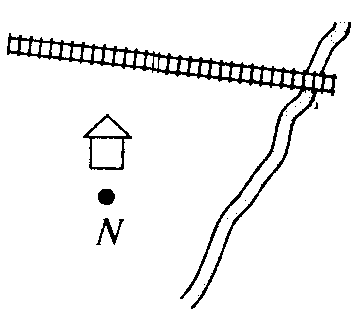
Подводит итог того, что ученики уже много знают и умеют. Нацеливает на систематизацию материала и применение умений к решению задач. Подводит учащихся к формулированию цели и задач урока, предлагая решить следующую задачу на слайде презентации.
Как провести через пункт N дорогу, чтобы расстояние по ней от этого пункта до железной дороги и до канала были равны?
Решают задачу. Обсуждают полученный результат.
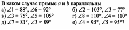
Организация и самоорганизация учащихся в ходе усвоения материала. Организация обратной связи.
УУД:1.2, 2.2-2.4, 3.1, 3.2
Организация деятельности учащихся по освоению учебной информации на уровне «знание».
Предлагает сверить свои выводы и догадки с определением в учебнике.
Сегодня мы познакомимся с новой геометрической фигурой - параллелограммом, с его свойствами. Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам. В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке. Все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида.
Самостоятельно формулируют определение параллелограмма. Работают в парах. Проверяют себя по учебнику стр.101.
Желательно, чтобы дети создали собственные формулировки, сравнив их с книжными. Формулировки должны быть верными по смыслу, а не по форме.
Выделяют существенные признаки понятия и записывают их в тетрадь:
1) четырехугольник;
2) одна пара противоположных сторон параллельна;
3) другая пара противоположных сторон параллельна
Учебник стр. 101
Первичное закрепление
УУД: 1.3, 2.2., 2.3., 3.1, 3.2, 4.3
Отработка определения параллелограмма в процессе решения устных задач
Предлагает определить какие из предложенных четырехугольников являются параллелограммом
На готовых чертежах определяют какие из четырехугольников являются параллелограммами, а какие нет и почему.
2
1
4
3
5
6
Решение задач
УУД:1.2, 1.3, 2.2, 2.3, 3.1-3.3, 4.1
Организация деятельности учащихся по освоению учебной информации на уровне «умения»
Предлагает типовые задачи.
Наводящие вопросы:
Какой четырехугольник называется параллелограммом?
Что нужно доказать, чтобы АВСD был параллелограммом?
Когда прямые будут параллельными?
Решают задачи. Выделяют признаки объекта
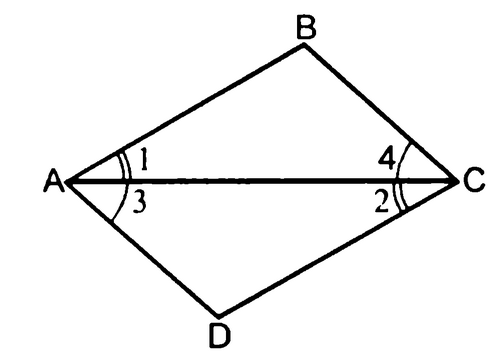
Дано: 1=2, 3=4.
Доказать: АВСD - параллелограмм
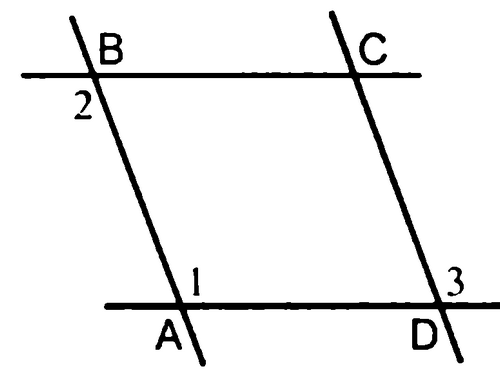
Дано: 1=2=3.
Доказать: АВСD - параллелограмм
Подведение итогов.
Рефлексия.
Домашнее задание.
УУД:1.4, 4.2.
Проведение самоанализа и самооценки собственной деятельности. Обеспечить понимание учащимися цели, содержания и способов выполнения домашнего задания.
Организовывает подведение итогов. Даёт качественную оценку работы класса и отдельных учащихся. Записывает домашнее задание: п. 42 в. 6, № 376
Повторяют, что узнали, какие умения и навыки отрабатывали и закрепляли.
Анализируют качество собственной работы на уроке, отвечая на вопрос: «Что нового я узнал?»
Осознают продвижение в своём умственном развитии, отвечая на вопрос: «Что называется параллелограммом?».
Записывают домашнее задание в дневники
На экране вопросы:
Что нового я узнал?
Что называется параллелограммом?
Конспект фрагмента урока по геометрии в 8 классе
Предмет: геометрия, класс: 8, авторы учебника: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
Тема урока: Параллелограмм (п. 42).
Всего часов на тему: 3
Номер урока в теме: 2
Тип урока: урок смешанного типа
Цели урока:
-
Образовательные: изучить свойства параллелограмма, решение задач на использование свойств параллелограмма;
-
Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
-
Воспитательные: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.
-
Планируемые образовательные результаты
-
Предметные
-
Метапредметные результаты (УУД)
-
Личностные
Регулятивные
Познавательные
Коммуникативные
Знать: определение параллелограмма и его свойства
Уметь: доказывать, что противоположные стороны и углы параллелограмма равны, диагонали пересекаются и точкой пересечения делятся пополам выполнять чертежи по условию задачи, находить углы и стороны параллелограмма, используя свойства углов и сторон
1.1. принимать учебную задачу; 1.2. планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану; 1.3. контролировать процесс и результаты деятельности, вносить необходимые коррективы; 1.4. адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления.
2.1. осознавать познавательную задачу; 2.2. читать и слушать, извлекая нужную информацию, понимать информацию, выполнять УУД; 2.3. осуществлять для решения учебных задач операции анализа, синтеза, сравнения; 2.4. устанавливать причинно-следственные связи, делать выводы.
3.1. вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения; 3.2. задавать вопросы, слушать и отвечать на вопросы других, формулировать собственные мысли, высказывать и обосновывать свою точку зрения; 3.3. строить небольшие монологические высказывания; 3.4. осуществлять совместную деятельность в парах и рабочих группах с учётом конкретных учебно-познавательных задач.
4.1. положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся; 4.2. осознавать свои трудности и стремиться к их преодолению; 4.3. осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
Организационная структура урока
Этапы урока
Задачи этапа
Деятельность учителя
Деятельность учащихся
Средства: учебник, интерактивная доска
Организационный момент
УУД:4.1
Вхождение в тему урока и создание условий для осознанного восприятия нового материала
УУД: 1.3, 1.4, 2.2, 3.1-3.3, 4.1, 4.2.
Повторение опорных знаний.
Фронтальный опрос:
Предлагает решение задач на готовых чертежах
Необходимо вспомнить следующие темы: признаки равенства треугольников, свойства углов при параллельных прямых, определение параллелограмма.
Необходимо вспомнить следующие умения: доказывать равенство треугольников, находить равные углы при параллельных прямых
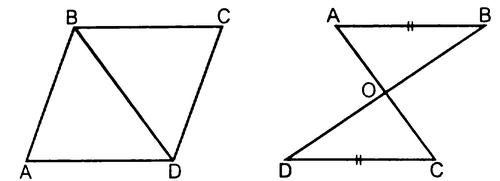
1. Дано: АВСD, ВСАD
Доказать: ВС=АD, А=С
2. Дано: АВСD, АВ=СD
Доказать: О - середина АС и ВD
3. Дано: АВСD - параллелограмм. Что вы можете сказать о взаимном расположении сторон
АВ и СD, ВС и АD? Что вы можете сказать об углах А и В?
Организация и самоорганизация учащихся в ходе усвоения материала. Организация обратной связи.
УУД:1.2, 2.2-2.4, 3.1, 3.2
Организация деятельности учащихся по освоению учебной информации на уровне «знание».
Распределить учащихся в небольшие группы для решения следующих задач:
Рассмотрите противоположные стороны, углы и диагонали параллелограмма.
Что вы можете сказать о противолежащих сторонах и углах параллелограмма?
Что можно сказать о точке пересечения диагоналей параллелограмма?
Обсуждение свойств параллелограмма с доказательствами.
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма делятся точкой пересечения пополам
3.В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°
Последнее свойство также может быть выдвинуто учащимися, хотя в учебнике его нет.
Работают в группах
Устно приводят алгоритм выполнения задания
Делают чертежи.
Выделяют условия и заключения теорем.
Доказывают теоремы.
В
А
D
А1. Дано: АВСD - параллелограмм
Док-ть: АВ=СD,
ВС=АD,
С
ВА=С, В=D
О2.
А
D
Дано: АВСD - параллелограмм
АС и ВD - диагонали
АС ∩ ВD = О
Доказать: АО=ОС, ВО=ОD
Решение задач
УУД:1.2, 1.3, 2.2, 2.3, 3.1-3.3, 4.1
Организация деятельности учащихся по освоению учебной информации на уровне «умения»
Организует работу по выполнению теста.
Выполняют тест на применение полученных знаний.
По эталону сверяют ответы теста.
1. Чему равна сумма углов параллелограмма:
а) 180°, б)90°, в) 360°, г) 720°.
2. Если одна сторона параллелограмма равна 10 см, а другая - 20 м, то периметр его равен:
а) 10 см, б) 20 см, в) 30 см, г) 60 см, д) 120 см.
3. Если стороны параллелограмма равны 3 и 5 см, то какие эти стороны:
а) соседние, б) противоположные, в) любые?
4. Если один угол параллелограмма равен 42°, то чему равны другие его углы:
а) 42° и 82°, б) 42°, 84°, 54°, в) 42°, 138°, 138°, г) 84° и 138°?
5. Сумма двух углов параллелограмма равна 100°. Какие эти углы:
а) соседние, б) противоположные, в) любые?
6. Если диагональ параллелограмма образует с его сторонами углы 30° и 40°, то углы параллелограмма равны:
а) 60° и 80°, б) 70° и 10°, в) 70° и 110°.
Подведение итогов.
Рефлексия.
Домашнее задание.
УУД:1.4, 4.2.
Конспект фрагмента урока по геометрии в 8 классе
Предмет: геометрия, класс: 8, авторы учебника: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.
Тема урока: Прямоугольник (п. 45).
Всего часов на тему: 2
Номер урока в теме: 1
Тип урока: урок изучения нового материала
Цели урока:
образовательная: повторить понятие прямоугольника, опираясь на полученные ранее знания учащихся; рассмотреть свойства прямоугольника как частного вида параллелограмма и научить учащихся применять их в процессе решения задач.
развивающая: развитие логического мышления, творческого мышления, умения анализировать, развитие пространственных представлений, математической речи;
воспитательная: прививать учащимся интерес к предмету, формировать умения аккуратно и грамотно выполнять математические записи и чертежи; учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности.
-
Планируемые образовательные результаты
-
Предметные
-
Метапредметные результаты (УУД)
-
Личностные
Регулятивные
Познавательные
Коммуникативные
Знать: определение прямоугольника, его элементы, свойства Уметь: различать на чертеже среди четырехугольников доказывать, что данный четырехугольник является прямоугольником, выполнять чертежи по условию задачи, находить в прямоугольнике угол между диагоналями, используя свойство диагоналей
1.1. принимать учебную задачу; 1.2. планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану; 1.3. контролировать процесс и результаты деятельности, вносить необходимые коррективы; 1.4. адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления.
2.1. осознавать познавательную задачу; 2.2. читать и слушать, извлекая нужную информацию, понимать информацию, выполнять УУД; 2.3. осуществлять для решения учебных задач операции анализа, синтеза, сравнения; 2.4. устанавливать причинно-следственные связи, делать выводы.
3.1. вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения; 3.2. задавать вопросы, слушать и отвечать на вопросы других, формулировать собственные мысли, высказывать и обосновывать свою точку зрения; 3.3. строить небольшие монологические высказывания; 3.4. осуществлять совместную деятельность в парах и рабочих группах с учётом конкретных учебно-познавательных задач.
4.1. положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся; 4.2. осознавать свои трудности и стремиться к их преодолению; 4.3. осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
Организационная структура урока
Этапы урока
Задачи этапа
Деятельность учителя
Деятельность учащихся
Средства: учебник, интерактивная доска, рабочая тетрадь.
Организационный момент
УУД:4.1
"Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия". Эти слова, сказанные великим французским архитектором Ле Корбюзье, в начале ХХ века очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука.
"Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия".
Ле Корбюзье
Вхождение в тему урока и создание условий для осознанного восприятия нового материала
УУД: 1.3, 1.4, 2.2, 3.1-3.3, 4.1, 4.2.
Повторение опорных знаний. Мотивация учебной деятельности.
Фронтальный опрос:
Дайте определение параллелограмма.
Является ли параллелограмм выпуклым четырехугольником?
Каким свойством обладают противоположные стороны параллелограмма?
Каким свойством обладают противоположные углы параллелограмма?
Каким свойством обладают диагонали параллелограмма?
Необходимо вспомнить определение и свойства параллелограмма
УУД:1.1, 2.1, 2.2-2.4,3.1-3.3, 4.1
Определение темы, цели и задач урока.
Приведите примеры предметов, в окружающей обстановке, имеющих форму прямоугольника
Приводят примеры
Организация и самоорганизация учащихся в ходе усвоения материала. Организация обратной связи.
УУД:1.2, 2.2-2.4, 3.1, 3.2
Организация деятельности учащихся по освоению учебной информации на уровне «знание».
Сделайте чертёж прямоугольника в тетради
Каково взаимное расположение противоположных сторон прямоугольника?
А мы уже встречались с четырехугольником, у которого противоположные стороны попарно параллельны, как называется такая фигура?
Какой мы можем сделать вывод о прямоугольнике? Как можно назвать прямоугольник?
А что его отличает от параллелограмма? У него все углы прямые, т. е. равны.
Мы с вами дали определение прямоугольника, давайте попробуем его сформулировать: прямоугольником называется параллелограмм, у которого все углы прямые. Давайте проверим, правы ли мы, откройте, пожалуйста, учебник на стр.108 и прочитайте определение, данное в учебнике.
Отметить, что определение прямоугольника в учебнике избыточное. Чтобы параллелограмм являлся прямоугольником, достаточно, чтобы один из его углов был прямым.
Так как прямоугольник - параллелограмм, то какими свойствами параллелограмма он обладает?
Рассмотреть особое свойство диагоналей прямоугольника.
Чертят прямоугольник.
Формулируют определение прямоугольника. Проверяют себя по учебнику стр.108.
Формулируют свойства прямоугольника.
Знакомятся с особым свойством диагоналей прямоугольника и доказывают его
Формулируют обратное утверждение и доказывают его.
Проверяют доказательство по учебнику.
Учебник стр. 108, тетрадь
Первичное закрепление
УУД: 1.3, 2.2., 2.3., 3.1, 3.2, 4.3
Организует работу учащихся в рабочих тетрадях.
Проверяет правильность решения.
Работают в рабочих тетрадях. Самостоятельно решают задачу №23
По окончании работы один из учащихся читает свое решение.
Идет обсуждение правильности решения
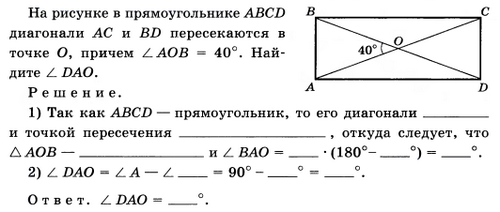
Проверка полученных результатов
УУД: 1.3, 1.4, 2.2, 4.2, 4.3
Организация деятельности учащихся по осознанию ими результата освоения учебной информации.
Вызывает ученика к доске для решения задачи №401(б)
Наводящие вопросы:
-
Биссектриса АК отсекает от прямоугольника треугольник АКD. Что вы можете сказать об этом треугольнике?
-
Сколько решений имеет задача?
Решают на доске и в тетрадях задачу №401(б)
Учебник №401(Найдите периметр прямоугольника АВСD, если биссектриса угла А делит сторону DС на отрезки 2,7 дм и 4,5 дм.)
Подведение итогов.
Рефлексия.
Домашнее задание.
УУД:1.4, 4.2.
Проведение самоанализа и самооценки собственной деятельности. Обеспечить понимание учащимися цели, содержания и способов выполнения домашнего задания.
Организовывает подведение итогов. Даёт качественную оценку работы класса и отдельных учащихся. Записывает домашнее задание: п. 45 в. 12-13 № 399, № 400.
Заполняют пропуски на карточках, лежащих на столах.
Карточка.
Прямоугольником называется _____, у которого все углы _____.
Свойство прямоугольника: _____ прямоугольника равны.
Признак прямоугольника: если в параллелограмме диагонали _____, то этот параллелограмм - _____.
ЗАКЛЮЧЕНИЕ
В данном проекте была проделана следующая работа:
-
Выявлены теоретические основы обучения теме «Четырехугольники», связанные с реализацией ФГОС ООО.
-
Выполнен отбор средств обучения теме «Четырехугольники», в том числе средства ИКТ.
-
Разработана таблица целей и карта обучения теме «Четырехугольники».
-
Составлена учебная рабочая программа «Тематическое и почасовое планирование образовательных результатов освоения темы «Четырехугольники»
-
Разработаны методические рекомендации обучения теме «Четырехугольники» и показано применение их в учебном процессе на примере трех фрагментов уроков, иллюстрирующих развитие и формирование УУД при обучении данной теме школьного курса математики.
Список литературы
-
Асмолов А. Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А. Г. Асмолова. - М.: Просвещение, 2010. - 159 с.
-
Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Некрасов В.Б., Юдина И.И. Изучение геометрии в 7-9 класса: Методические рекомендации к учебнику. Книга для учителя. М.: Дрофа,2003
-
Боженкова Л.И. Методика формирования универсальных учебных действий при обучении геометрии. - М.: БИНОМ, 2013. - 205 с.
-
Болтянский В.Г. Геометрические преобразования плоскости /Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. Сост. И.Л. Никольская. - М.: Просвещение, 1991.
-
Болтянский В.Г. Движения плоскости / Школа в Кванте. Геометрия / Под редакцией А.А.Егорова. - М.: Бюро Квантум, 1995 (Приложение к журналу «Квант» - 1995. - № 1).
-
Болтянский В.Г. Паркет из четырехугольников //Квант. - 1989. - № 11.
-
Г. И. Глейзер. История математики в школе. Пособие для учителей. М.: «Просвещение», 1964.
-
Гейдман Б. Осевая симметрия //Приложение к журналу «Квант» № 1/1995. - М.: Бюро «Квантум», 1995.
-
Гончарова С.Г., Кукин Г.П. Конструктор «В мире симметрии» /Математика в школе./ - 1996. - № 3.
-
Готман Э.Г. Задачи по планиметрии и методы их решения. - М.: Просвещение, 1996.
-
Данилюк А. Я., Кондаков А. М., Тишков В. А.. Концепция духовно-нравственного развития и воспитания личности гражданина России. - М.: Просвещение, 2009. - 24 с.
-
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. М.: ИЛЕКСА, 2010
-
Заславский А. Паркеты и разрезания //Квант. - 1999. - № 2.
-
Зеркальная симметрия //Квант. - 1992. - № 3.
-
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 8 класса. М.: Просвещение, 2004
-
Квадрат //Квант. - 1989. - № 5.
-
Кордемский Б.А., Русалев Н.В. Удивительный квадрат. - М.: Столетие, 1994.
-
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. Геометрия, 7-9 классы: учеб. для общеобразоват. учреждений. М.: Просвещение, 2010
-
Лоповок Л.М. Тысяча проблемных задач по математике: Книга для учащихся. - М.: Просвещение, 1995.
-
Н. Ф. Гаврилова. Поурочные разработки по геометрии: 8 класс. М.: ВАКО, 2010
-
Прасолов В.В. Задачи по планиметрии. Часть I. - 2-е изд. - М.: Наука, 1991.
-
Примерные программы по математике. - М.: Просвещение, 2010. - 67 с.
-
Рабинович Е.М. Задачи и упражнения на готовых чертежах. Москва-Харьков: ИЛЕКСА, 1998
-
С. А. Козлова, А. Г. Рубин, В. А. Гусев. Геометрия 7-9 классы. М.: БАЛАСС, 2013.
-
Семенов Е.Е. За страницами учебника геометрии. - 2-е изд. - М.: Просвещение, 1999, с. 143.
-
Сергеев И.Н. и др. Примени математику. - М.: Наука, 1989.
-
Смирнова И.М. В мире многогранников. - М.: Просвещение, 1995.
-
Смирнова И.М., Смирнов В.А. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. - М.: Мнемозина, 2005.
-
Соловейчик С.А.. Педагогика для всех. - Первое сентября, 2000. - 143 с.
-
Тарасов Л.В. Этот удивительно симметричный мир. - М.: Просвещение, 1982.
-
Федеральный государственный образовательный стандарт общего основного образования / М-во образования и науки Рос. Федерации. - М.: Просвещение, 2011. - 48 с
-
Фундаментальное ядро содержания общего образования. / Под ред. В.В.Козлова, А.М. Кондакова. - М.: Просвещение, 2011.
-
Энциклопедия для детей. Математика. Том 11. - М.: Аванта, 2001.
Интернет-ресурсы
-
- каталог электронных образовательных ресурсов ФЦ.
-
- электронные образовательные ресурсы.
-
- сайт Министерства образования и науки РФ.
-
- каталог Единой коллекции цифровых образовательных ресурсов.
-
- ФГОС общего образования и разработанные к ним документы.
-
- электронные образовательные ресурсы.
-
Перечень учебник учебников по математике, рекомендованных к использованию
-
- портал "Информационно-коммуникационные технологии в образовании".
-
- сайт ФГУ "Государственный научно-исследовательский институт информационных технологий и телекоммуникаций".
-
- «Сеть творческих учителей».
-
Национальная образовательная инициатива «Наша новая школа» - http://mon.gov.ru/dok/akt/6591
-
Федеральная целевая программа развития образования на 2011-2015 годы - http://mon.gov.ru/press/news/8286