Учителю
Рабочая программа 7-9 класс по алгебре по учебнику Г.В.Дорофеева, С.Б.Суворовой и др

Рабочая программа 7-9 класс по алгебре по учебнику Г.В.Дорофеева, С.Б.Суворовой и др

Автор публикации: Бутузова О.В.

Дата публикации: 21.09.2016

Краткое описание:

предварительный просмотр материала

Муниципальное бюджетное общеобразовательное учреждение

«Гимназия №8» г. Шумерля Чувашской Республики

Рассмотрено на заседании МО учителей математики, информатики, робототехники

Протокол №

Руководитель МО О.В. Бутузова __________________

«Согласовано»

Зам. директора по УВР

«Утверждаю»:

Рабочая программа

по алгебре

в 7-9 классах

на 2016 - 2017 учебный год

Программа разработана на основе федерального компонента государственного стандарта основного общего образования

Составители: Бутузова Ольга Викторовна

учитель математики

высшей категории;

г. Шумерля, 2016

Содержание:

Пояснительная записка

Данная рабочая программа курса по алгебре для 7-9 классов разработана на основе учебного плана МБОУ «Гимназия №8» с учетом требований федерального компонента государственного стандарта основного общего образования.

Цели

Изучение алгебры направлено на достижение следующих целей:

овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критического мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математики как к части общечеловеческой культуры, играющей особую роль в общественном развитии..

Место учебного предмета в учебном плане.

Реализация рабочей программы рассчитана на 35 учебных недель. В рабочей программе предусмотрено 6 контрольных работ.

Осуществление представленной рабочей программы предполагает использование следующего учебно-методического комплекта:

Описание ценностных ориентиров содержания учебного предмета.

Изучение алгебры позволяет формировать умения и навыки умственного труда - планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе изучения алгебры школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.

Важнейшей задачей школьного курса алгебры является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в алгебре правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Тем самым алгебра занимает одно из ведущих мест в формировании научно-теоретического мышления школьников. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вносит значительный вклад в эстетическое воспитание учащихся.

Требования к уровню подготовки учащихся 7-9 классов

Учащиеся должны знать:

значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира;

учащиеся должны уметь:

выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путём систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях.

владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной.

способны решать следующие жизненно-практические задачи: Самостоятельно приобретать и применять знания в различных ситуациях, работать в группах, аргументировать и отстаивать свою точку зрения, уметь слушать других, извлекать учебную информацию на основе сопоставительного анализа объектов, пользоваться предметным указателем энциклопедий и справочников для нахождения информации, самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем.

Общая характеристика учебного предмета

Целью изучения курса алгебры в VII - IX классах является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса учащиеся овладевают приемами вычислений на калькуляторе.

Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.

Учебники соответствуют федеральным компонентам Государственного стандарта общего образования.

В курсе алгебры можно выделить следующие основные содержательные линии: арифметика; алгебра; функции; вероятность и статистика. Наряду с этим в содержание включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные содержательные линии. При этом первая линия - «Логика и множества» - служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая - «Математика в историческом развитии» - способствует созданию общекультурного, гуманитарного фона изучения курса.

Содержание линии «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе.

Содержание линии «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разделов математики, смежных предметов и окружающей реальности. Язык алгебры подчёркивает значение математики как языка для построения математических моделей процессов и явлений реального мира.

Развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивных рассуждений также являются задачами изучения алгебры. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.

Раздел «Вероятность и статистика» - обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности - умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.

Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

Содержание учебного предмета.

7 класс

1. Дроби и проценты

Обыкновенные и десятичные дроби, вычисления с рациональными числами. Степень с натуральным показателем. Решение задач на проценты. Статистические характеристики: среднее арифметическое, мода, размах.

Основная Цель - систематизировать и обобщить сведения об обыкновенных и десятичных дробях, обеспечить на этой основе дальнейшее развитие вычислительных навыков, умение решать задачи на проценты; сформировать первоначальные умения статистического анализа числовых данных.

В соответствии с идеологией курса данная тема представляет собой блок арифметических вопросов. Основное внимание уделяется дальнейшему развитию вычислительной культуры: отрабатываются умения находить десятичные эквиваленты или десятичные приближения обыкновенных дробей, выполнять действия с числами, в том числе с использованием калькулятора. Продолжается начатая в 6 классе работа по вычислению числовых значений буквенных выражений. Вычислительные навыки учащихся получают дальнейшее развитие при изучении степени с натуральным показателем; учащиеся должны научиться находить значения выражений, содержащих действие возведения в степень, а также записывать большие и малые числа с использованием степеней числа 10. Продолжается решение задач на проценты. Однако в этой теме рассматриваются более сложные по сравнению с предыдущим годом задачи.

Основное содержание последнего блока темы - знакомство с некоторыми статистическими характеристиками. Учащиеся должны научиться в несложных случаях находить среднее арифметическое, моду и размах числового ряда.

2. Прямая и обратная пропорциональности

Представление зависимости между величинами с помощью формул. Прямо пропорциональная и обратно пропорциональная зависимости. Пропорции, решение задач с помощью пропорций.

Основная Цель- сформировать представления о прямой и обратной пропорциональностях величин; ввести понятие пропорции и научить учащихся использовать пропорции при решении задач.

Изучение темы начинается с обобщения и систематизации знаний учащихся о формулах, описывающих зависимости между величинами. Вводится понятие переменной, которое с этого момента.должно активно использоваться в речи учащихся. В результате изучения материала учащиеся должны уметь осуществлять перевод задач на язык формул, выполнять числовые подстановки в формулы, выражать переменные из формул. Особое внимание уделяется формированию представлений о прямой и обратной пропорциональной зависимостях и формулам, выражающим такие зависимости между величинами. Формируется представление о пропорции и решении задач с помощью пропорций.

3. Введение в алгебру

Буквенные выражения. Числовые подстановки в буквенное выражение. Преобразование буквенных выражений: раскрытие скобок, приведение подобных слагаемых.

Основная Цель - сформировать у учащихся первоначальные представления о языке алгебры, о буквенном исчислении; научить выполнять элементарные базовые преобразования буквенных выражений.

В 7 классе начинается систематическое изучение алгебраического материала и данная тема представляет собой первый проход соответствующего блока вопросов.

Введение буквенных равенств мотивируется опытом работы с числами, осознанием и обобщением приемов вычислений. На этом этапе раскрывается смысл свойств арифметических действий как законов преобразований буквенных выражений, формируются умения упрощать несложные произведения, раскрывать скобки, приводить подобные слагаемые.

4. Уравнения

Уравнения. Корни уравнения. Линейное уравнение. Решение текстовых задач методом составления уравнения.

Основная Цель - познакомить учащихся с понятиям и уравнения и корня уравнения, с некоторыми свойствами уравнений; сформировать умение решать несложные линейные уравнения с одной переменной; начать обучение решению текстовых задач алгебраическим способом.

Целесообразно, чтобы уравнение в курсе появилось как способ перевода фабульных ситуаций на математический язык. Такому переводу должно быть уделено достаточное внимание. Следует рассмотреть некоторые приемы составления уравнения по условию задачи, возможность составления разных уравнений по одному и тому же условию, сформировать умение выбирать наи50лее предпочтительный для конкретной задачи вариант уравнения. Переход к алгебраическому методу решения задач одновременно служит мотивом для обучения способу решения уравнений. Основное внимание в этой теме уделяется решению линейных уравнений с одной переменной, показываются некоторые технические приемы решения.

5. Координаты и графики

Числовые промежутки. Расстояние между точками на координатной прямой. Множества точек на координатной плоскости. Графики зависимостей у = х, у = х², у = х³, у = I х I . Графики реальных зависимостей.

Основная Цель - развить умения, связанные с работой а координатной прямой и на координатной плоскости; познакомить с графиками зависимостей

у = х, у = -х, у = х², У = х³, У = 1 х1; сформировать первоначальные навыки интерпретации графиков реальных зависимостей.

При изучении курса математики в 5-6 классах учащиеся познакомились с идеей координат. В этой теме делается следующий шаг: рассматриваются различные множества точек на координатной прямой и на координатной плоскости, при этом формируется умение переходить от алгебраического описания множества точек к геометрическому изображению и наоборот. Рассматривается формула расстояния между точками координатной прямой.

При изучении темы учащиеся знакомятся с графиками таких зависимостей, как у = х, у = -х, у = х², У = х³, У = I х1. В результате учащиеся должны уметь достаточно быстро строить каждый из перечисленных графиков, указывая его характерные точки. Сформированные умения могут стать основой для выполнения заданий на построение графиков кусочно-заданных зависимостей.

Специальное внимание в данной теме уделяется работе с графиками реальных зависимостей - температуры, движения и пр., причем акцент должен быть сделан на считывание с графика нужной информации. Важно, чтобы учащиеся получили представление об использовании графиков в самых различных областях человеческой деятельности.

6. Свойства степени с натуральным показателем

Произведение и частное степеней с натуральными показателями. Степень степени, произведения и дроби. Решение комбинаторных задач, формула перестановок.

Основная Цель - выработать умение выполнять действия над степенями с натуральными показателями; научить применять правило умножения при решении комбинаторных задач.

Учащимся уже знакомо определение степени с натуральным показателем, и у них есть некоторый опыт преобразования выражений, содержащих степени, на основе определения. Основное содержание данной темы состоит в рассмотрении свойств степени и выполнении действий со степенями. Сформированные умения могут найти применение при выполнении заданий на сокращение дробей, числители и знаменатели которых - произведения, содержащие степени.

В этой же теме продолжается обучение решению комбинаторных задач, в частности задач, решаемых на основе комбинаторного правила умножения. Дается специальное название одному из видов комбинаций - перестановки и рассматривается формула для вычисления числа перестановок. Это первая комбинаторная формула, сообщаемая учащимся.

7. Многочлены

Одночлены и многочлены. Сложение, вычитание и умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности.

Основная Цель - выработать умения выполнять действия с многочленами, применять формулы квадрата суммы и квадрата разности, куба суммы и куба разности для преобразования квадрата и куба двучлена в многочлен.

Изучение данной; темы опирается на знания, полученные при изучении темы «Введение в алгебру». Используются свойства алгебраических сумм и произведений, правила раскрытия скобок и приведения подобных слагаемых. Терминами «одночлен» и «многочлен» называются такие алгебраические выражения, с которыми учащиеся, по сути, уже имели дело.

Основное внимание в данной теме уделяется рассмотрению алгоритмов выполнения действий над многочленами - сложения, вычитания, умножения, при этом подчеркивается следующий теоретический факт: сумму, разность и произведение многочленов всегда можно представить в виде многочлена. В ходе практической деятельности учащиеся должны выполнить задания комплексного характера, предусматривающие выполнение нескольких действий. Однако следует иметь в виду, что на этом этапе основным результатом является овладение собственно алгоритмами действий над многочленами, а преобразованиям целых выражений будет уделено внимание еще и в 8 классе. Овладение действиями с многочленами сопровождается развитием умений решать линейные уравнения и применять алгебраический метод решения текстовых задач.

8. Разложение многочленов на множители

Вынесение общего множителя за скобки. Способ группировки.

Формула разности квадратов, формулы суммы кубов и разности кубов. Решение уравнений с помощью разложения на множители.

Основная Цель - выработать умение выполнять разложение на множители с помощью вынесения общего множителя за скобки и способом группировки, а также с применением формул сокращенного умножения.

Вопрос о разложении многочленов на множители дается в виде отдельной темы, в которую отнесено также знакомство с формулами разности квадратов, разности и суммы кубов. Рассматриваются некоторые специальные приемы преобразования многочленов, после которых становится возможным применение способа группировки: разбиение какого-то члена многочлена на два слагаемых и более, а также прием «прибавить - вычесть».

Важно, чтобы формируемый аппарат нашел применение. Поэтому в ходе изучения темы целесообразно продолжить формирование умений сокращать дроби и рассмотреть приемы решения уравнений на основе равенства произведения нулю.

9. Частота и вероятность

Частота случайного события. Оценка вероятности случайного события по его частоте. Сложение вероятностей.

Основная Цель - показать возможность оценивания вероятности случайного события по его частоте.

Особенностью предлагаемой методики является статистический подход к понятию вероятности: вероятность случайного события оценивается по его частоте при проведении достаточно большой серии экспериментов. Такой подход требует реального проведения опытов в ходе учебного процесса. Так как для стабилизации частоты необходимо большое число экспериментов, то рекомендуется такая форма урока, как работа в малых группах. Процесс стабилизации частоты полезно иллюстрировать с помощью графика.

8класс

Алгебраические дроби

Алгебраическая дробь. Основное свойство алгебраической дроби. Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей. Степень с целым показателем и ее свойства. Выделение множителя - степени десяти-в записи числа.

Основная цель - сформировать умения выполнять действия с алгебраическими дробями, действия со степенями с целым показателем; развить навыки решения текстовых задач алгебраическим методом.

Эта тема является естественным продолжением и развитием начатого в 7 классе систематического изучения преобразований рациональных выражений. Изложение целесообразно строить, как и при изучении преобразований буквенных выражений в 7 классе, с опорой на опыт работы с числами. Главным результатом обучения должно явиться владение алгоритмами сложения, вычитания, умножения и деления алгебраических дробей. Количество и уровень сложности заданий, требующих выполнения нескольких действий, определяются самим учителем в зависимости от возможностей класса. При этом необходимо иметь в виду, что в соответствии с общей идеей развития содержания курса по спирали в 9 классе предусмотрен еще один «проход» преобразования рациональных выражений.

Самостоятельный фрагмент темы посвящен изучению степени с целым показателем. Мотивом для введения этого понятия служит целесообразность представления больших и малых чисел в, так называемом стандартном виде. С этим способом записи чисел учащиеся уже встречались на уроках физики.

Завершается тема фрагментом, посвященным решению уравнений и текстовых задач. По сравнению с курсом 7 класса здесь предлагаются более сложные в техническом отношении уравнения (хотя, как и в 7 классе, это по-прежнему целые уравнения, но содержащие дробные коэффициенты).

2. Квадратные корни

Квадратный корень из числа. Понятие об иррациональном числе. Десятичные приближения квадратного корня. Свойства арифметического квадратного корня и их применение к преобразованию выражений. Корень третьей степени, понятие о корне п-й степени из числа. Нахождение приближенного значения корня с помощью калькулятора. График зависимости у=

Основная цель - научить преобразованиям выражений, содержащих квадратные корни; на примере квадратного и кубического корней сформировать представления о корне n-й степени.

Понятие квадратного корня возникает в курсе при обсуждении двух задач геометрической (о нахождении стороны квадрата по его площади) и алгебраической (о числе корней уравнения вида х² = а, где а - произвольное число). При рассмотрении первой из них даются начальные представления об иррациональных числах.

В содержание темы целесообразно включить нетрадиционный для алгебры вопрос - теорему Пифагора. Это позволит продемонстрировать естественное применение квадратных корней для нахождения длин отрезков, построения отрезков с иррациональными длинами, точек с иррациональными координатами.

Целесообразно также активно использовать калькулятор, причем не только в качестве инструмента для извлечения корней, но и как средство, позволяющее проиллюстрировать некоторые теоретические идеи.

В ходе изучения данной темы предусматривается знакомство с понятием кубического корня, одновременно формируются начальные представления о корне n-й степени. Рассматривается график зависимости у=.

3. Квадратные уравнения

Квадратное уравнение. Формулы корней квадратного уравнения. Решение текстовых задач составлением квадратных уравнений. Теорема Виета. Разложение на множители квадратного трехчлена.

Основная цель - научить решать квадратные уравнения и использовать их при решении текстовых задач.

В тему включен весь материал, традиционно относящийся к этому разделу курса. В то же время предлагаются и некоторые существенные изменения: рассмотрение теоремы Виета связывается с задачей разложения квадратного трехчлена на множители; в систему упражнений должны постоянно включаться задания на решение уравнений высших степеней; следует активно использовать метод подстановки.

Большое место должно быть отведено решению текстовых задач, при этом рассматриваются некоторые особенности математических моделей, описывающих реальные ситуации.

В связи с рассмотрением вопроса о разложении на множители квадратного трехчлена появляется возможность для дальнейшего развития линии преобразований алгебраических выражений.

4. Системы уравнений

Уравнение с двумя переменными. Линейное уравнение с двумя переменными и его график. Примеры решения уравнений в целых числах. Система уравнений; решение систем двух линейных уравнений с двумя переменными, графическая интерпретация. Примеры решения нелинейных систем. Решение текстовых задач составлением систем уравнений. Уравнение с несколькими переменными.

Основная цель - ввести понятия уравнения с двумя переменными, графика уравнения, системы уравнений; обучить решению систем линейных уравнений с двумя переменными, а также использованию приема составления систем уравнений при решении текстовых задач.

Основное содержание данной темы курса связано с рассмотрением линейного уравнения и решением систем линейных уравнений. В то же время приводятся примеры и нелинейных уравнений, рассматриваются их графики, решаются системы, в которых одно уравнение не является линейным.

Особенностью изложения является акцентирование внимания на блоке вопросов, по сути относящихся к аналитической геометрии. Тема начинается с вопроса о прямых на координатной плоскости: рассматривается уравнение прямой в различных формах, специальное внимание уделяется уравнению вида, формулируется условие параллельности прямых, а в качестве необязательного материала может быть рассмотрено условие перпендикулярности прямых. Сформированный аналитический аппарат применяется к решению задач геометрического содержания (например, составление уравнения прямой, проходящей через две данные точки, прямой, параллельной данной и проходящей через данную точку.

Продолжается решение текстовых задач алгебраическим методом. Теперь математической моделью рассматриваемой ситуации является система уравнений, при этом в явном виде формулируется следующая мысль: при переводе текстовой задачи на математический язык удобно вводить столько переменных, сколько неизвестных содержится в условии.

5. Функции

Функция. Область определения и область значений функции. График функции. Возрастание и убывание функции, сохранение знака на промежутке, нули функции. Функции и их графики. Примеры графических зависимостей, отражающих реальные процессы.

Основная цель - познакомить учащихся с понятием функции, расширить математический язык введением функциональной терминологии и символики; рассмотреть свойства и графики конкретных числовых функций: линейной функции и функции; показать значимость функционального аппарата для моделирования реальных ситуаций, научить в несложных случаях применять полученные знания для решения прикладных и практических задач.

Материал данной темы опирается на умения, полученные в результате работы с графиками реальных зависимостей между величинами. Акцент делается не столько на определение понятия функции и связанных с ним понятий, сколько на введение нового языка, новой терминологии и символики. При этом новый язык постоянно сопоставляется с уже освоенным: внимание обращается на умение переформулировать задачу или вопрос, перевести их с языка графиков на язык функций либо уравнений.

Особенностью данной темы является прикладная направленность учебного материала. Основное внимание уделяется графикам реальных зависимостей, моделированию разнообразных реальных ситуаций, формированию представления о скорости роста или убывания функции. При изучении линейной функции следует явно сформулировать мысль о том, что линейной функцией описываются процессы, протекающие с постоянной скоростью, познакомить учащихся с идеей линейной аппроксимации.

6. Вероятность и статистика

Статистические характеристики ряда данных, медиана, среднее арифметическое, размах. Таблица частот. Вероятность равновозможных событий. Классическая формула вычисления вероятности события и условия ее применения. Представление о геометрической вероятности.

Основная цель - сформировать представление о возможностях описания и обработки данных с помощью различных средних; познакомить учащихся с вычислениями вероятности случайного события с помощью классической формулы и из геометрических соображений.

Материал данной темы знакомит с ситуациями, требующими вычисления средних для адекватного описания ряда данных. Основное внимание уделяется целесообразности использования моды, медианы или среднего арифметического в зависимости от ситуации.

В предыдущих классах был рассмотрен статистический подход к понятию вероятности, на основе которого вводится гипотеза о равновероятности событий, позволяющая в ситуации с равновозможными исходами применять классическую формулу вычисления вероятности события. Кроме того, рассматривается геометрический подход к понятию вероятности, позволяющий в некоторых ситуациях с бесконечным количеством исходов вычислять вероятность наступления события как отношения площадей фигур.

7. Повторение

В ходе изучения алгебры 8 класса учащиеся должны уметь в изучаемых главах:

Алгебраические дроби. Конструировать алгебраические выражения. Находить область определения алгебраической дроби; выполнять числовые подстановки и вычислять значение дроби, в том числе с помощью калькулятора. Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей. Выполнять действия с алгебраическими дробями. Применять преобразования выражений для решения задач. Выражать переменные из формул (физических, геометрических, описывающих бытовые ситуации). Проводить исследования, выявлять закономерности. Формулировать определение степени с целым показателем. Формулировать, записывать в символической форме и иллюстрировать примерами свойства степени с целым показателем; применять свойства степени для преобразования выражений и вычислений. Использовать запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивать числа и величины, записанные с использованием степени 10. Выполнять вычисления с реальными данными. Выполнять прикидку и оценку результатов вычислений. Решать уравнения с дробными коэффициентами, решать текстовые задачи алгебраическим методом.

Квадратные корни. Формулировать определения квадратного корня из числа. Применять график функции у=х² для нахождения корней квадратных уравнений, используя при необходимости калькулятор; проводить оценку квадратных корней. Строить график функции у= 1/х, исследовать по графику её свойства. Доказывать свойства арифметических квадратных корней; применять их к преобразованию выражений. Вычислять значения выражений, содержащих квадратные корни; выполнять знаково-символические действия с использованием обозначений квадратного и кубического корня. Исследовать уравнение х² = а, находить точные и приближённые корни при а > 0. Формулировать определение корня третьей степени; находить значения кубических корней, при необходимости используя калькулятор.

Квадратные уравнения. Распознавать квадратные уравнения, классифицировать их. Выводить формулу корней квадратного уравнения. Решать квадратные уравнения - полные и неполные. Проводить простейшие исследования квадратных уравнений. Решать уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной. Наблюдать и анализировать связь между корнями и коэффициентами квадратного уравнения. Формулировать и доказывать теорему Виета, а также обратную теорему, применять эти теоремы для решения разнообразных задач. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления уравнения; решать составленное уравнение; интерпретировать результат. Распознавать квадратный трёхчлен, выяснять возможность разложения на множители, представлять квадратный трёхчлен в виде произведения линейных множителей. Применять различные приёмы самоконтроля при выполнении преобразований. Проводить исследования квадратных уравнений с буквенными коэффициентами, выявлять закономерности.

Системы уравнений. Определять, является ли пара чисел решением уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными. Решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целые решения путём перебора. Распознавать линейные уравнения с двумя переменными; строить прямые - графики линейных уравнений; извлекать из уравнения вида у=кх+l информацию о положении прямой в координатной плоскости. Распознавать параллельные и пересекающиеся прямые по их уравнениям; конструировать уравнения прямых, параллельных данной прямой. Использовать приёмы самоконтроля при построении графиков линейных уравнений. Решать системы двух линейных уравнений с двумя переменными; использовать графические представления для исследования систем линейных уравнений; решать простейшие системы, в которых одно из уравнений не является линейным. Применять алгебраический аппарат для решения задач на координатной плоскости. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений; решать составленную систему уравнений; интерпретировать результат.

Функции. Вычислять значения функций, заданных формулами (при необходимости использовать калькулятор); составлять таблицы значений функций. Строить по точкам графики функций. Описывать свойства функции на основе её графического представления. Моделировать реальные зависимости формулами и графиками. Читать графики реальных зависимостей. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Использовать компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды изучаемых функций. Показывать схематически расположение на координатной плоскости графиков функций вида у=кх, у=кх + b, y = k/x в зависимости от значений коэффициентов, входящих в формулы. Строить графики изучаемых функций; описывать их свойства/

Вероятность и статистика. Характеризовать числовые ряды с помощью различных средних. Находить вероятности событий при равновозможных исходах; решать задачи на вычисление вероятностей с применением комбинаторики. Находить геометрические вероятности.

9 класс

1.Неравенства

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.

Цель - выработать умения решать линейные неравенства с одной переменной и их системы.

Знать определение числового неравенства с одной переменной, что называется решением неравенства с одной переменной, что значит решить неравенство, свойства числовых неравенств, понимать формулировку задачи «решить неравенство».

Уметь записывать и читать числовые промежутки, изображать их на числовой прямой, решать линейные неравенства с одной переменной, решать системы неравенств с одной переменной.

Уметь применять свойства неравенства при решении неравенств и их систем.

2. Квадратичная функция

Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция y=ax² + bx + с, её свойства, график. Простейшие преобразования графиков функций. Решение неравенств второй степени с одной переменной. [Решение рациональных неравенств методом интервалов.]

Цель - выработать умение строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной.

Знать основные свойства функций, уметь находить промежутки знакопостоянства, возрастания, убывания функций

Уметь находить область определения и область значений функции, читать график функции

Уметь решать квадратные уравнения, определять знаки корней

Уметь выполнять разложение квадратного трехчлена на множители

Уметь строить график функции у=ах^{2 ,} выполнять простейшие преобразованияграфиков функций

Уметь строить график квадратичной функции, выполнять простейшие преобразования графиков функций

Уметь строить график квадратичной функции» находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения.

Уметь построить график функции y=ax² и применять её свойства. Уметь построить график функции y=ax² + bx + с и применять её свойства

Уметь находить токи пересечения графика Квадратичной функции с осями координат. Уметь разложить квадратный трёхчлен на множители.

Уметь решать квадратное уравнение.

Уметь решать квадратное неравенство алгебраическим способом. Уметь решать квадратное неравенство с помощью графика квадратичной функции

Уметь решать квадратное неравенство методом интервалов. Уметь находить множество значений квадратичной функции.

Уметь решать неравенство ах² +вх+с.≥0 на основе свойств квадратичной функции.

3. Уравнения и системы уравнений

Целое уравнение и его корни. Решение уравнений третьей и четвертой степени с одним неизвестным с помощью разложения на множители и введения вспомогательной переменной. Дробное уравнение и его корни.

Уравнение с двумя переменными и его график. Уравнение окружности. Решение систем, содержащих одно уравнение первой, а другое второй степени. Решение задач методом составления систем. Решение систем двух уравнений второй степени с двумя переменными.

Уравнения с параметрами и методы их решения. Графики дробно- линейных функций.

Цель - выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными, и решать текстовые задачи с помощью составления таких систем.

Знать методы решения уравнений:

а) разложение на множители;

б) введение новой переменной;

в)графический способ.

Уметь решать целые уравнения методом введения новой переменной

Уметь решать системы 2 уравнений с 2 переменными графическим способом

Уметь решать уравнения с 2 переменными способом подстановки и сложения

Уметь решать задачи «на работу», «на движение» и другие составлением систем уравнений.

4. Прогрессии

Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии.

Цель - дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.

Добиться понимания терминов «член последовательности», «номер члена последовательности», «формула n -го члена арифметической прогрессии»

Знать формулу n -го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии

Уметь применять формулу суммы n -первых членов арифметической прогрессии при решении задач

Знать, какая последовательность является геометрической, уметь выявлять, является ли последовательность геометрической, если да, то находить q

Уметь вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии

Уметь применять формулу при решении стандартных задач

Уметь применять формулу S= при решении практических задач

Уметь находить разность арифметической прогрессии

Уметь находить сумму n первых членов арифметической прогрессии. Уметь находить

любой член геометрической прогрессии. Уметь находить сумму n первых членов геометрической прогрессии. Уметь решать задачи.

5. Элементы статистики и теории вероятностей

Комбинаторные задачи. Перестановки, размещения, сочетания. Перестановки. Размещения. Сочетания Вероятность случайного события

Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими.

Уметь пользоваться формулой комбинаторики при вычислении вероятностей.

7. Повторение. Решение задач

Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 9 класса)

Планируемые результаты обучения.

В ходе преподавания математики в основной школе, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

- планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;

- решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

- исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

- ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

- проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

- поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Система оценки индивидуальных достижений обучаемых.

Оценка письменных работ

Оценка «5»

выполнил работу в полном объеме с соблюдением необходимой последовательности действий;
в ответе правильно и аккуратно выполняет все записи, таблицы, рисунки, чертежи, графики, вычисления;
правильно выполняет анализ ошибок.

Оценка «4» ставится, если выполнены требования к оценке 5, но допущены 2-3 недочета, не более одной ошибки и одного недочета.

Оценка «3» ставится, если

• работа выполнена не полностью, но объем выполненной части таков, что позволяет получить правильные результаты и выводы;

• в ходе проведения работы были допущены ошибки.

Оценка «2» ставится, если

• работа выполнена не полностью и объем выполненной работы не позволяет сделать правильных выводов;

• работа проводилась неправильно;

• ученик совсем не выполнил работу.

Оценка устных ответов

Оценка «5» ставится в том случае, если учащийся

• правильно понимает сущность вопроса, дает точное определение и истолкование основных понятий;

• правильно анализирует условие задачи, строит алгоритм решения;

• строит ответ по собственному плану, сопровождает ответ новыми примерами, умеет применить знания в новой ситуации;

• может установить связь между изучаемым и ранее изученным материалом из курса алгебры, а также с материалом, усвоенным при изучении других предметов.

Оценка «4» ставится, если

• ответ ученика удовлетворяет основным требованиям к ответу на оценку 5, но дан без использования собственного плана, новых примеров, без применения знаний в новой ситуации, без использования связей с ранее изученным материалом и материалом, усвоенным при изучении других предметов;

• учащийся допустил одну ошибку или не более двух недочетов и может их исправить самостоятельно или с небольшой помощью учителя.

Оценка «3» ставится, если учащийся

• правильно понимает сущность вопроса, но в ответе имеются отдельные пробелы в усвоении вопросов курса алгебры, не препятствующие дальнейшему усвоению программного материала;

• умеет применять полученные знания при решении простых задач по готовому алгоритму;

• допустил не более одной грубой ошибки и двух недочетов, не более одной грубой и одной негрубой ошибки, не более двух-трех негрубых ошибок, одной негрубой ошибки и трех недочетов;

• допустил четыре-пять недочетов.

Оценка «2» ставится, если учащийся не овладел основными знаниями и умениями в соответствии с требованиями программы и допустил больше ошибок и недочетов, чем необходимо для оценки 3;

• ставится в том случае, если ученик не может ответить ни на один из поставленных вопросов.

Грубые ошибки.

К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять, незнание приемов решения задач, рассматриваемых в учебных пособиях, а также вычислительные ошибки, если он не являются опиской.

Негрубые ошибки.

К негрубым ошибкам относятся:

- потеря корня или сохранение в ответе постороннего корня;

- отбрасывание без объяснения одного из корня и равнозначные им.

К недочетам относятся:

нерациональное решение, описки, недостаточность;
отсутствие пояснений, обоснований в решениях;
если одна и та же ошибка (один и тот же недочет) встречаются несколько раз, то это рассматривается как одна ошибка (один недочет);
зачеркивание в работе (желательно, чтобы они были аккуратными) свидетельствует о поисках решения, что считать ошибкой не следует.

Учебно-тематический план для 7а, 7б, 7в классов

Учебно-тематический план в 8а классе,

Алгебра, 4 ч в неделю, всего - 140 чКонструировать алгебраические выражения.

Находить область определения алгебраической дроби;

выполнять числовые подстановки и вычислять значение дроби, в том числе с помощью калькулятора.

Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей.

Выполнять действия с алгебраическими дробями.

Применять преобразования выражений для решения задач.

Выражать переменные из формул (физических, геометрических, описывающих бытовые ситуации).

Проводить исследования, выявлять закономерности.

Формулировать определение степени с целым показателем.

Формулировать, записывать в символической форме и иллюстрировать примерами свойства степени с целым показателем; применять свойства степени для преобразования выражений и вычислений.

Использовать запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире.

Сравнивать числа и величины, записанные с использованием степени 10.

Выполнять вычисления с реальными данными.

Выполнять прикидку и оценку результатов вычислений.

Решать уравнения с дробными коэффициентами, решать текстовые задачи алгебраическим методом.

1.1

Что такое алгебраическая дробь

1.2

Основное свойство дроби

1.3

Сложение и вычитание алгебраических дробей

1.4

Умножение и деление алгебраических дробей

1.5

Преобразование выражений, содержащих алгебраические дроби

1.6

Степень с целым показателем

1.7

Свойства степени с целым показателем

1.8

Решение уравнений и задач

1.9

Сокращение дробей

Контрольная работа по теме «Алгебраические дроби»

Глава 2. Квадратные корни

Формулировать определения квадратного корня из числа.

Применять график функции у=х² для нахождения корней квадратных уравнений, используя при необходимости калькулятор.

Проводить оценку квадратных корней.

Строить график функции у = Vx.

Исследовать по графику её свойства.

Доказывать свойства арифметических квадратных корней.

Применять их к преобразованию выражений.

Вычислять значения выражений, содержащих квадратные корни.

Выполнять знаково-символические действия с использованием обозначений квадратного и кубического корня.

Исследовать уравнение х² = а, находить точные и приближённые корни при а> 0.

Формулировать определение корня третьей степени.

Находить значения кубических корней, при необходимости используя калькулятор.

2.1

Задача о нахождении стороны квадрата

2.2

Иррациональные числа

2.3

Теорема Пифагора

2.4

Квадратный корень (алгебраический подход)

2.5

График зависимости

2.6

Свойства квадратных корней

2.7

Преобразование выражений, содержащих квадратные корни

2.8

Кубический корень

2.9

Двойные радикалы

Контрольная работа по теме «Квадратные корни»

Глава 3. Квадратные уравнения

Распознавать квадратные уравнения, классифицировать их.

Выводить формулу корней квадратного уравнения.

Решать квадратные уравнения - полные и неполные.

Проводить простейшие исследования квадратных уравнений.

Решать уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной.

Наблюдать и анализировать связь между корнями и коэффициентами квадратного уравнения.

Формулировать и доказывать теорему Виета, а также обратную теорему, применять эти теоремы для решения разнообразных задач.

Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления уравнения.

Решать составленное уравнение.

Интерпретировать результат.

Распознавать квадратный трёхчлен, выяснять возможность разложения на множители, представлять квадратный трёхчлен в виде произведения линейных множителей.

Применять различные приёмы самоконтроля при выполнении преобразований.

Проводить исследования квадратных уравнений с буквенными коэффициентами, выявлять закономерности.

3.1

Какие уравнения называют квадратными

3.2

Формула корней квадратного уравнения

3.3

Вторая формула корней квадратного уравнения

3.4

Решение задач

3.5

Неполные квадратные уравнения

3.6

Теорема Виета

3.7

Разложение квадратного трехчлена на множители

3.8

Целые корни уравнения с целыми коэффициентами

Контрольная работа по теме «Квадратные уравнения»

Глава 4. Системы уравнений

Распознавать линейные уравнения с двумя переменными.

Строить прямые - графики линейных уравнений.

Извлекать из уравнения вида y = kx + l информацию о положении прямой в координатной плоскости.

Распознавать параллельные и пересекающиеся прямые по их уравнениям.

Конструировать уравнения прямых, параллельных данной прямой.

Использовать приёмы самоконтроля при построении графиков линейных уравнений.

Решать системы двух линейных уравнений с двумя переменными.

Использовать графические представления для исследования систем линейных уравнений.

Решать простейшие системы, в которых одно из уравнений не является линейным.

Применять алгебраический аппарат для решения задач на координатной плоскости.

Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путём составления системы уравнений.

Решать составленную систему уравнений.

Интерпретировать результат.

4.1

Линейное уравнение с двумя переменными

4.2

График линейного уравнения с двумя переменными

4.3

Уравнение прямой вида y=kx+l

4.4

Системы уравнений. Решение систем способом сложения

4.5

Решение систем уравнений способом подстановки

4.6

Решение задач с помощью систем уравнений

4.7

Задачи на координатной плоскости

4.8

Геометрическая интерпретация неравенств с двумя переменными

Контрольная работа по теме «Системы уравнений»

Глава 5. Функции

Вычислять значения функций, заданных формулами (при необходимости использовать калькулятор).

Составлять таблицы значений функций. Строить по точкам графики функций. Описывать свойства функции на основе её графического представления.

Моделировать реальные зависимости формулами и графиками.

Читать графики реальных зависимостей.

Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий.

Строить речевые конструкции с использованием функциональной терминологии.

Использовать компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу.

Распознавать виды изучаемых функций.

Показывать схематически расположение на координатной плоскости графиков функций вида y=kx, у=кх + Ь, к У = - , в зависимости от значений коэффициентов, входящих в формулы.

Строить графики изучаемых функций, описывать их свойства

5.1

Чтение графиков

5.2

Что такое функция

5.3

График функции

5.4

Свойства функции

5.5

Линейная функция

5.6

Функция и ее график

5.7

Целая и дробная части числа

Контрольная работа по теме «Функции»

Глава 6. Вероятность и статистика

Характеризовать числовые ряды с помощью различных средних.

Находить вероятности событий при равновозможных исходах; решать задачи на вычисление вероятностей с применением комбинаторики.

Находить геометрические вероятности.

6.1

Статистические характеристики

6.2

Вероятность равновозможных событий

6.3

Сложные эксперименты

6.4

Геометрические вероятности

Глава 6. Алгебраические уравнения

Многочлены от одной переменной

Уравнения высших степеней

Рациональные уравнения

Уравнения с модулем

Иррациональные уравнения

Задачи с параметрами

Промежуточная аттестация

Повторение

Всего

140

Учебно-тематический план в 8б,8в классах,

Алгебра, 3 часа в неделю, всего 105 часовАлгебраические дроби

Что такое алгебраическая дробь
1. Основное свойство дроби
2. Сложение и вычитание алгебраических дробей
3. Умножение и деление алгебраических дробей
4. Преобразование выражений, содержащих алгебраические дроби
5. Степень с целым показателем
6. Свойства степени с целым показателем
7. Решение уравнений и задач

Контрольная работа по теме «Алгебраические дроби»

Квадратные корни

Задача о нахождении стороны квадрата

1. Иррациональные числа
2. Теорема Пифагора
3. Квадратный корень - алгебраический подход
4. График зависимости у=
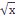
5. Свойства квадратных корней
6. Преобразование выражений, содержащих квадратные корни
7. Кубический корень

Контрольная работа по теме «Квадратные корни»

Квадратные уравнения

Какие уравнения называют квадратными

1. Формула корней квадратного уравнения
2. Вторая формула корней квадратного уравнения
3. Решение задач
4. Неполные квадратные уравнения
5. Теорема Виета
6. Разложение квадратного трёхчлена на множители

Контрольная работа по теме «Квадратные уравнения»

Системы уравнений

Линейное уравнение с двумя переменными

1. График линейного уравнения с двумя переменными
2. Уравнение прямой вида у=kx+l
3. Системы уравнений. Решение систем с помощью сложения
4. Решение систем уравнений с помощью подстановки
5. Решение задач с помощью систем уравнений
6. Задачи на координатной плоскости

Контрольная работа по теме «Системы уравнений»

Функции

Чтение графиков

1. Что такое функция
2. График функции
3. Свойства функции
4. Линейная функция
5. Функция y=k/x и её график

Контрольная работа по теме «Функции»

Вероятность и статистика

Статистические характеристики

1. Вероятность равновозможных событий
2. Сложные эксперименты
3. Геометрические вероятности

Промежуточная аттестация

Повторение

Учебно - тематическое планирование по алгебре

к учебнику под редакцией Г.В. Дорофеева, С.Б. Суворовой

« Алгебра - 9»Рецензирование ответов, Математический тест, с/р

Контроль знаний

Регулятивные:

самостоятельно ставить новые учебные цели и задачи;

при планировании достижения целей самостоятельно и адекватно учитывать условия и средства их достижения;

выделять альтернативные способы достижения цели и выбирать наиболее эффективный способ.

Познавательные: ориентироваться на разнообразие способов решения задач; извлекать необходимую информацию из учебно-научных текстов;

самостоятельная работа с

источниками информации, анализ обобщения и систематизации полученной информации; развитие умения производить аргументированные рассуждения, проводить обобщение.

владеют навыками самоанализа и самоконтроля

Коммуникативные:

учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; формулировать собственное мнение и позицию, аргументировать и координировать еѐ с позициями партнѐ-ров в сотрудничестве при вы-работке общего решения в со-вместной деятельности

ИРК

2/2

Действительные числа

ФО, ИДР

3/3

Действительные числа (3)

ИДР

4/4

Общие свойства неравенств

ИДР

5/5

Общие свойства неравенств

ОСР

6/6

Решение линейных неравенств

СР

7/7

Решение линейных неравенств

ИРК

8/8

Решение линейных неравенств

ФО, ИДР

9/9

Решение линейных неравенств

ИДР

10/10

Решение линейных неравенств (5)

ФО

11/11

Решение систем линейных неравенств

ИДР

12/12

Решение систем линейных неравенств

ИРК

13/13

Решение систем линейных неравенств (3)

ФО

14/14

Доказательство неравенств

ИДР

15/15

Доказательство неравенств

СР

16/16

Доказательство неравенств (3)

ФО

17/17

Что означают слова «с точностью до …»

ФО

18/18

Что означают слова «с точностью до …»

ИДР

19/19

Контрольная работа № 1 « Неравенства»

Контроль знаний

Глава II. Квадратичная функция (20 ч)

20/1

Какую функцию называют квадратичной

Анализ ошибок Рецензирование ответов Математический диктант, наблюдение, с/р, работа с книгой, анализ графиков

Регулятивные:

вносить необходимые

коррективы в действие после

его завершения на основе учета характера сделанных ошибок; определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий.

Познавательные:

владеть общим приемом решения задач; самостоятельное выделение и формулирование познавательной цели; поиск и выделение необходимой информации;

моделирование; применение методов информационного поиска, в том числе с помощью компьютерных средств; структурирование знаний;

Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов;

способность к мобилизации сил и энергии; способность к волевому усилию - к выбору в ситуации мотивационного конфликта и к преодолению препятствий.

ИДР

21/2

Какую функцию называют квадратичной

СР

22/3

Какую функцию называют квадратичной

ФО, ИДР

23/4

Какую функцию называют квадратичной (4)

ФО, ДРЗ

24/5

График и свойства функции y = ax²

СР

25/6

График и свойства функции y = ax²

ИДР

26/7

Сдвиг графика функции y = ax² вдоль осей координат

ИДР

27/8

Сдвиг графика функции y = ax² вдоль осей координат

СР

28/9

Сдвиг графика функции y = ax² вдоль осей координат

ФО, ИДР

29/10

Сдвиг графика функции y = ax² вдоль осей координат

ИДР

30/11

Сдвиг графика функции y = ax² вдоль осей координат (5)

СР

31/12

График функции y = ax² + bx+ c

ФО, ИДР

32/13

График функции y = ax² + bx+ c

ФО, ДРЗ

33/14

График функции y = ax² + bx+ c

СР

34/15

График функции y = ax² + bx+ c (4)

ИДР

35/16

Квадратные неравенства

ИДР

36/17

Квадратные неравенства

ИДР

37/18

Квадратные неравенства

СР

38/19

Квадратные неравенства

ФО, ИДР

39/20

Контрольная работа № 2 «Квадратные корни»

Контроль знаний

Глава III. Уравнения и системы уравнений (25 ч)

40/1

Рациональные выражения

Анализ ошибок, Математический диктант, тест, с/р, рецензирование ответов, работа с книгой, компетентностно-ориентированные задания.

Контроль знаний, наблюдение, построение графиков, анализ графиков,

Регулятивные: учитывать правило в планировании и контроле способа решения; построение математических моделей;

поиск нужной информации по заданной теме в источниках различного типа.

Познавательные:

осуществлять расширенный поиск информации с исполь-зованием ресурсов библиотек и Интернета;

создавать и преобразовывать

модели и схемы для решения задач;

осуществлять выбор наиболее эффективных способов реше-ния задач в зависимости от конкретных условий;

Коммуникативные:

устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и де-лать выбор;

аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом;

задавать вопросы, необходи-мые для организации собст-венной деятельности и со-трудничества с партнѐром

ФО, ИДР

41/2

Рациональные выражения

42/3

Рациональные выражения

ОСР

43/4

Рациональные выражения (4)

ДРЗ

44/5

Целые уравнения

ФО, ИДР

45/6

Целые уравнения

ОСР

46/7

Дробные уравнения

СР

47/8

Дробные уравнения

ИДР

48/9

Дробные уравнения

СР

49/10

Дробные уравнения (4)

ФО, ИДР

50/11

Решение задач, на составление дробных уравнений

51/12

Решение задач, на составление дробных уравнений

ОСР

52/13

Решение задач, на составление дробных уравнений

ДРЗ

53/14

Решение задач, на составление дробных уравнений (3)

ФО, ИДР

54/15

Контрольная работа № 3 «Рациональные выражения. Уравнения»

ОСР

55/16

Системы уравнений с двумя переменными

СР

56/17

Системы уравнений с двумя переменными

ИДР

57/18

Системы уравнений с двумя переменными

СР

58/19

Системы уравнений с двумя переменными (4)

ФО, ИДР

59/20

Решение задач, на составление системы уравнений

60/21

Решение задач, на составление системы уравнений

ОСР

61/22

Графическое исследование уравнений

ДРЗ

62/23

Графическое исследование уравнений

ФО, ИДР

63/24

Графическое исследование уравнений

ОСР

64/25

Контрольная работа № 4 «Системы уравнеий»

Контроль знаний

Глава IV. Арифметическая и геометрическая прогрессии (17 ч )

65/1

Числовые последовательности

Анализ ошибок

Рецензирование ответов, с/р, решение задач

Регулятивные:

выделение и осознание учащимся того что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; сличение способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона.

Познавательные:

осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы; осознанное и произвольное построение речевого высказывания;

выбор наиболее эффективных способов решения учебных задач;

рефлексия способов и условий действия, контроль и оценка процесса результатов деятельности;

Коммуникативные:

учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; способность к мобилизации сил и энергии;

способность к волевому усилию - к выбору в ситуации мотивационного конфликта и к преодолению препятствий.

ИДР

66/2

Числовые последовательности

ИРК

67/3

Арифметическая прогрессия

ФО

68/4

Арифметическая прогрессия

ИДР

69/5

Арифметическая прогрессия (3)

ФО

70/6

Сумма первых п членов арифметической прогрессии

ФО

71/7

Сумма первых п членов арифметической прогрессии

ИДР

72/8

Сумма первых п членов арифметической прогрессии (3)

СР, Т

73/9

Геометрическая прогрессия

СР

74/10

Геометрическая прогрессия

ФО, ИДР

75/11

Геометрическая прогрессия (3)

ИДР

76/12

Сумма первых п членов геометрической прогрессии

ФО

77/13

Сумма первых п членов геометрической прогрессии

ИДР

78/14

Простые и сложные проценты

СР

79/15

Простые и сложные проценты

СР

80/16

Простые и сложные проценты (3)

ФО

81/17

Контрольная работа № 5 «Арифметическая и геометрическая прогрессии»

Контроль знаний

Глава V. Статистика и вероятность(6 ч )

82/1

Выборочные исследования

Рецензирование ответов, анализ графиков, таблиц, схем.

Регулятивные: выделение и осознание учащимся того что

уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; сличение способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона.

Познавательные:

выбор наиболее эффективных способов решения учебных задач;

рефлексия способов и условий действия, контроль и оценка процесса результатов

деятельности;

Коммуникативные:

учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве

деятельности;

Коммуникативные:

учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве

ФО

83/2

Интервальный ряд. Гистограмма

ИДР

84/3

Характеристики разброса

ФО

85/4

Статистическое исследование и прогноз

ИДР

86/5

Вероятность и комбинаторика

ФО

87/6

Вероятность и комбинаторика

ИРК

Промежуточная аттестация

Контроль знаний

Повторение (15 ч)

89/1

Сложение и вычитание алгебраических дробей