Конспект урока по геометрии на тему Площадь параллелограмма

План-конспект урока по геометрии в 8 классе

Учителя математики МБОУ «Гимназии №1 им. К.Д.Ушинского»

Совер Татьяны Юрьевны

Тема урока: Площадь параллелограмма.

Тип урока: урок изучения нового материала, первичного закрепления знаний и формирования умений и навыков.

Учебник: Геометрия 7-9, авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.

Оборудование: тетради, учебники, интерактивная доска, карточки для выполнения групповой работы.

Цель урока: изучить теорему о площади параллелограмма, научиться делать теоретические обобщения, проводить классификацию, развивать логику мышления при решении специально подобранных разноуровневых задач, воспитывать потребность в доказательстве высказанной гипотезы.

Задачи урока:

• образовательная: вывести формулу для вычисления площади параллелограмма и показать применение этой формулы в процессе решения задач, совершенствовать навыки решения задач.

• развивающая: развитие у учащихся самостоятельности, инициативы и творчества, способности к самоорганизации, точности и ясности речи; формирование навыка исследовательской, повышения уровня математической культуры учащихся.

• воспитательная: способствовать развитию любознательности и творческой активности обучающихся, развитие познавательного интереса, культуры математической речи, способности к объективному самоанализу, самооценке, воспитание толерантности и умения работать в группах.

Универсальные учебные действия:

• Личностные - осознание учащимися важности изучаемого материала, взаимосвязи данной темы с другими темами геометрии;

• Познавательные - умение извлекать нужную информацию из прочитанного текста, умение применять полученные знания на практике при решении задач и построении рисунков к ним;

• Коммуникативные - через диалоги умение слушать и грамотно излагать свое мнение;

• Регулятивные - взаимный контроль, самоконтроль (анализ, причины ошибок), контроль со стороны учителя.

Планируемый результат:

Знать:

• формулы нахождения площади параллелограмма;

• алгоритм решения задач на нахождение площади параллелограмма;

Уметь:

• применять алгоритм решения задач на составление квадратных уравнений на практике,

• применять удобный способ решения квадратных уравнений

• использовать различные источники знаний,

• работать с карточками различного содержания,

• работать в группах, индивидуально.

Используемые технологии: уровневой дифференциации, проблемно поисковой, ИКТ.

Ход урока:

«Считай несчастным тот день и тот час, в который ты не усвоил ничего нового и ничего не прибавил к образованию»

Ян Амос Каменский

Организационный момент

Проверка учителем домашнего задания (учащиеся отвечают по тетрадям).

Формулировка учителем целей урока.

Актуализация знаний.

Фронтально повторить (вопросы с рисунками на мультимедийной доске):

1. В каких единицах измеряется площадь?

2. Сформулируйте определение параллелограмма.

3. Сформулируйте признаки параллелограмма.

4. Сформулируйте свойства площадей.

5. Сформулируйте теорему о площади прямоугольника.

Устная работа (решение задач на готовых чертежах)

На мультимедийной доске выведено задание:

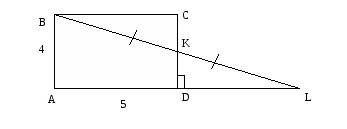
1) Дано: ABCD - прямоугольник, AK = KL. Найти .

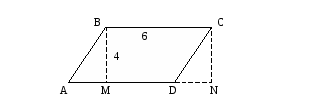
2) Дано: ABCD - параллелограмм, BM = 4 см, BC = 6 см,

Доказать: . Найти:

Работа по изучению нового материала.

Введем понятие высоты параллелограмма.

На мультимедийную доску выведен рисунок, который дети переносят в тетрадь.

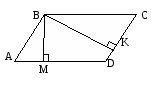
BK - высота, проведенная к стороне DC.

BM - высота, проведенная к стороне AD

Перпендикуляр, проведенный из любой точки одной стороны к прямой, содержащей противоположную сторону, называется высотой параллелограмма. Сторона, к которой проведена высота, называется - основанием, а перпендикуляр - высотой параллелограмма.

Теорема: Площадь параллелограмма равна произведению его основания на высоту.

Доказательство: Вернемся к задаче № 2. ABCD - параллелограмм с площадью S. Докажем, что . Докажем сначала, что площадь прямоугольника MBCN также равна S. Трапеция ABCN составлена из параллелограмма ABCD и треугольника DCN. С другой стороны она составлена из прямоугольника MBCN и треугольника ABM. Но прямоугольные треугольники ABM и DCN равны по гипотенузе и острому углу (Их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а , как соответственные при пересечении параллельных прямых AB и CD секущей AD) поэтому их площади равны. Следовательно площади параллелограмма ABCD и прямоугольника MBCN также равны. Т.е. площадь прямоугольника MBCN равна S. По теореме о площади прямоугольника . А так как BC = AD, то .Теорема доказана.

Физкультминутка

Учитель предлагает учащимся сделать перерыв на физкультминутку.

Поднимитесь на ноги, станьте в проходы. Потянитесь вверх и сделайте глубокий вдох. Задержитесь наверху и задержите дыхание на 3 секунды. Выдох, руки вниз и наклон вниз. Повторить 2 раза.

Встаньте ровно. Расслабьтесь. Закройте глаза. Поводите глазами вверх, вниз, влево, вправо. Откройте глаза.

Улыбнитесь друг другу. И с хорошим настроением продолжим работу.

Закрепление пройденного материала.

Работа у доски. Решают «сильные» ученики с подробным объяснением, остальные решают у себя в тетрадях. Учитель контролирует решение. По учебнику № 460, 461, 462, 464 (а).

Подведение итогов.

Рефлексия:

Учитель: С каким настроением вы уходите с урока?

Ученики поднимают сигнальные карточки.

</

Домашнее задание: из учебника: п. 52 № 463, 464 (б,в).