- Учителю
- Открытый урок в 8 классе по теме «Квадратные уравнения»
Открытый урок в 8 классе по теме «Квадратные уравнения»
Открытый урок в 8 классе по теме «Квадратные уравнения»
Эпиграф к уроку:
«Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным».
Паскаль
Цели:
-
Показать уровень усвоения программного материала по теме «Квадратные уравнения», навыки
-
решения квадратных уравнений с помощью применения формул корней квадратных
-
уравнений, изучить новый способ решения квадратных уравнений.
-
Развитие вычислительных навыков: навыков решения квадратных уравнений с помощью
-
формул, навыки нахождения дискриминанта квадратного уравнения, развитие логического
-
мышления,
-
Способствовать рациональной организации труда, внимательность, активное участие в учебно-
-
познавательном процессе, самостоятельность, самокритичность.
Оборудование к уроку: тест «Квадратные уравнения», интерактивная доска, таблицы, карточки.
План урока
-
Организационный момент «Настроимся на урок!»
-
Проверка домашнего задания
-
Тест «Квадратные уравнения».
-
Работа в парах: математика и биология, геометрия, физика.
-
Продвинутые способы решения квадратных уравнений
-
Викторина «Дальше, дальше…»
-
Итог.
Ход урока
1. Организационный момент «Настроимся на урок!»
Здравствуйте, ребята и гости нашего урока! Математику не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики - любознательность. Постараемся доказать это на уроке. Мы с вами начали изучать
новый большой раздел «Квадратные уравнения», на который отводится 20 уроков.
Сегодня четвертый урок из этой главы, однако, вы уже умеете решать квадратные уравнения. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.
Эпиграфом к уроку я взяла слова великого математика Паскаля «Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным». В течение урока мы еще вернемся к этим словам.
2. Проверка домашнего задания
Начнем урок с проверки домашнего задания.
Правильность решения заданий вы не сможете проверить, т. к. на предыдущем уроке каждый получил индивидуальное задание в зависимости от способностей и возможностей.
А вот знание теоретического материала, который понадобится нам на протяжении всего урока, давайте вспомним.
Какой вид имеет квадратное уравнение?
Какие уравнения вы знаете? (полные и неполные)
Сколько решений имеет полное квадратное уравнение? От чего это зависит?
3. Тест «Квадратные уравнения»
Итак, мы повторили, как можно решить квадратное уравнение. Сейчас я хотела бы проверить, как вы усвоили эти формулы и определения.
Ученики получают карточки с заданиями. Заполняют пропущенные слова в карточках.
I вариант
-
Уравнение вида ax2 + bx + c = 0, где a, b, c - заданные числа, a ≠ 0, x - переменная, называется…
-
Полное квадратное уравнение не имеет корней, если D…
-
Уравнение вида x2 + px + q = 0 называется…
-
Квадратное уравнение имеет два корня, если b2 - 4ac…
-
Дано уравнение 3x2 - 7x + 4 = 0. D =…
II вариант
-
Если квадратное уравнение ax2 + bx + c = 0, то a… коэффициент, c…
-
Уравнение x2 = a, где a
-
Полное квадратное уравнение имеет единственный корень, если…
-
Уравнение вида ax2 + c = 0, где a ≠ 0, c ≠ 0, называют… квадратным уравнением.
-
Дано уравнение x2 - 6x + 8 = 0. D =…
Проводится взаимопроверка. Ответы показываем через интерактивную доску.
4. Работа в парах
Вернемся к эпиграфу нашего урока. Попытаемся сделать математику хотя бы сегодня на уроке немного более занимательной.
Вам необходимо угадать, зашифрованное слово.
Математика и биология.
Учитель: Угадайте, что в ящике. Даю три определения этому предмету:
-
Непроизводная основа слова.
-
Число, которое после постановки его в уравнение обращает уравнение в тождество.
-
Один из основных органов растений.
/Корень/
Учитель: Вы должны определить, какого растения это корень, решив следующие уравнения в парах.
-
x2 - 8x + 15 = 0
-
x2 - 11x + 18 = 0
-
x2 - 5x - 6 = 0
-
x2 - 4x + 4 = 0
-
3x2 + 4x + 20 = 0
-
5x2 - 3x - 2 = 0
Учитель: Игра «Математическое лото». Найдите полученный ответ на экране. Проверить результат. Если ученики получают правильный ответ, то получат изображение розы, иначе - слайд с текстом «Проверьте решение».
Учитель: Что это за растение?
Ответ: Роза.
Учитель: Значит, в черном ящике лежал корень розы, о которой в народе говорят: «Цветы ангельские, а когти дьявольские». О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой.
Учитель: Видите, ребята, все в этом мире взаимосвязано: математика, русский язык и литература, биология. Мы увидели, что слово «корень» встречается на уроках биологии и математики. И не только.
Использование квадратных уравнений для решения задач по геометрии и физике.
Давайте узнаем, с какими еще предметами связано решение квадратных уравнений? Для этого решим следующие задачи и получим ответ на данный вопрос.
Задача1: Одна сторона прямоугольника на 5 м больше другой. Площадь его равна 36 м2 вычислите стороны прямоугольника.
Учитель: Каким способом будем решать задачу?
Ученики: Алгебраическим.
Учитель: Какую величину примем за неизвестное?
Ученики: Длину одной из сторон. Обозначим ее буквой х.
Учитель: чему равна длина другой стороны?
Ученики: х + 5
Учитель: чему равна площадь прямоугольника?
Ученики: произведение его длины на ширину.
Учитель: Какое уравнение можно составить по условию задачи?
Ученики: х(х+5)=36.
Ученики решают это уравнение в тетрадях самостоятельно, один из учеников комментирует решение вслух с места. х2+5х-36=0. х1= -9, х2=4. Число -9 не удовлетворяет условию задачи, так как х- длина отрезка, а она не может быть числом отрицательным. Ответ: b=4м, а=9м.
Этот пример показывает, что квадратные уравнения широко применяются при решении геометрических задач.
Задача 2: Определите, сколько времени будет падать камень, брошенный, вертикально с крыши дома с высоты 12 м?
Учитель: из курса физики вам известна формула 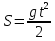 . Назовите величины входящие в нее.
. Назовите величины входящие в нее.
Ученики: S - расстояние, которое преодолевает тело(камень), t - время движения(падения) и g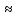 10м/с2 -ускорение свободного падения.
10м/с2 -ускорение свободного падения.
Учитель: какое уравнение получится после подстановки в формулу известных величин?
Ученики: 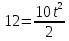 или 5
или 5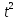 = 12.
= 12.
Задача свелась к решению неполного квадратного уравнения. Время падения камня t=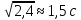 .
.
Ответ: 1,5с.
Этот пример из практики показывает применение квадратных уравнений в физике.
5. Продвинутые способы решения квадратных уравнений
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств, большого количества разных типов задач.
В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. В математической науке есть десять способов решения квадратных уравнений.
Способы решения квадратных уравнений, изучаемые в школе:
-
Разложение левой части на множители
-
Метод выделения полного квадрата
-
С применением формул корней квадратного уравнения
-
С применением теоремы Виета
-
Графический способ
Продвинутые способы решения квадратных уравнений:
-
Способ переброски
-
По свойству коэффициентов
-
С помощью циркуля и линейки
-
С помощью номограммы
-
Геометрический
Сегодня на уроке мы познакомимся с новым способом решения квадратных уравнений, который не изучается в школе. Но он очень интересный и вовсе не сложный.
Решение квадратных уравнений по свойству коэффициентов
Пусть дано квадратное уравнение ах2 + bх + с = 0, где, а ≠ 0.
Свойство 1
Если, а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = с/а
Свойство 2
Если а - b + с = 0, или b = а + с, то х1 = - 1, х2 = - с/а
Пример:
2x2 - 5x + 3 = 0 br>
3x2 + 4x +1 = 0
Решите самостоятельно:
1 вариант:
5x2 - 12x + 7 = 0
7x2 + 3x -4 = 0
2 вариант:
3x2 - 7x + 4 = 0
4x2 + 7x + 3 = 0
7. Викторина. «Дальше, дальше…»
В течение одной минуты ребята отвечают на вопросы, приведенные ниже:
-
Уравнение второй степени.
-
Сколько корней имеет квадратное уравнение, если D больше 0?
-
Равенство с переменной?
-
От чего зависит количество корней квадратного уравнения?
-
Как называется квадратное уравнение, у которого первый коэффициент - 1?
-
Сколько корней имеет квадратное уравнение, если дискриминант меньше 0?
-
Что значит решить уравнение?
-
Есть у любого слова, у растения и может быть у уравнения?
7. Итог урока
Учитель:
Что нового мы узнали на уроке?
Какое уравнение называется квадратным?
Какие виды квадратных уравнений вы знаете?
И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Оценивание учащихся. Сообщение домашнего задания.