Урок математики в 8 классе по теме «Теорема Виета»

Урок в 8 классе по теме

«Теорема Виета».

Цели урока:

• Выяснить зависимость между корнями и коэффициентами приведенного квадратного уравнения;

• Научиться применять эту зависимость для решения задач.

Для изучения новой темы нам необходимо повторить материал, сделаем это, разгадывая кроссворд.

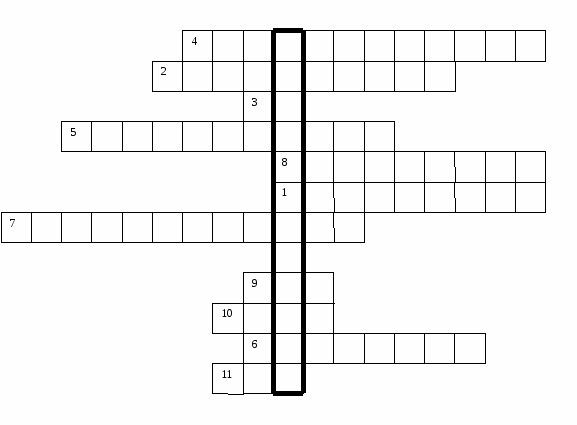
1. Равенство, содержащее переменную.

2. Уравнение вида ах² + bх + с = 0, где а, b, с - некоторые числа, х - переменная, а≠0.

3. Существенно ли условие а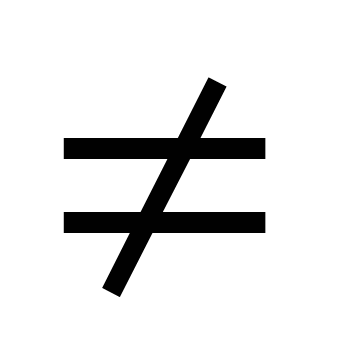0?

4. Как называются числа а, b, с?

5. Если а =1, то уравнение называется … .

6. Если в уравнении ах² + bх + с = 0, а ≠ 0, b = 0 или с = 0,то уравнение называется … .

7. От чего зависит наличие действительных корней квадратного уравнения?

8. Английский математик, которому принадлежит термин «Дискриминант».

9. Сколько корней имеет уравнение, если D > 0 .

10. Сколько корней имеет уравнение, если D = 0.

11. Существуют ли корни квадратного уравнения, если D < 0 .

Проверяем. (см. Презентацию)

В результате вы получили имя французского ученого, который впервые установил зависимость между корнями и коэффициентами квадратного уравнения, что мы сегодня попытаемся сделать. Кто же он - Франсуа Виет.

Итак, тема нашего урока «Теорема Виета».

Поверите ли вы мне, если я скажу, что данное уравнение х² - 2008х + 2007 = 0 смогу устно решить за несколько секунд и вы в конце урока тоже .

Какие же виды квадратных уравнений вам известны?

Заполните таблицу

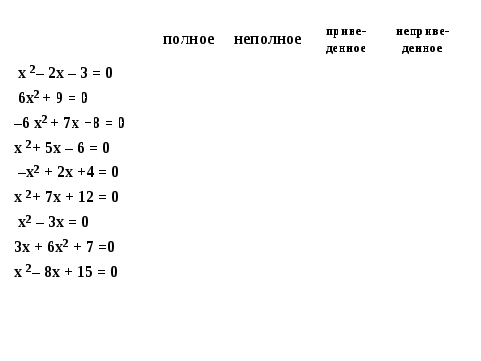
Сегодня мы с вами поведём речь о приведённых квадратных уравнениях, которые записывают ещё так: x² + px + q = 0.

Заполните таблицу:

Уравнение

p

q

х₁

х₂

х₁ + х₂

х₁ · х₂

1

х ²- 2х - 3 = 0

2

х ²+ 5х - 6 = 0

3

х ²- х - 12 = 0

4

х ²+ 7х + 12 = 0

Какое предположение можно сделать? Сравните сумму и произведением корней с коэффициентами уравнений. Какая существует зависимость между корнями приведенного квадратного уравнения и его коэффициентами? Сформулированное утверждение называется теоремой Виета.

Если приведённое квадратное уравнение x² + px + q = 0

имеет корни х₁ и х₂, то x₁ + x₂ = - p; x₁ ∙ x₂ = q.

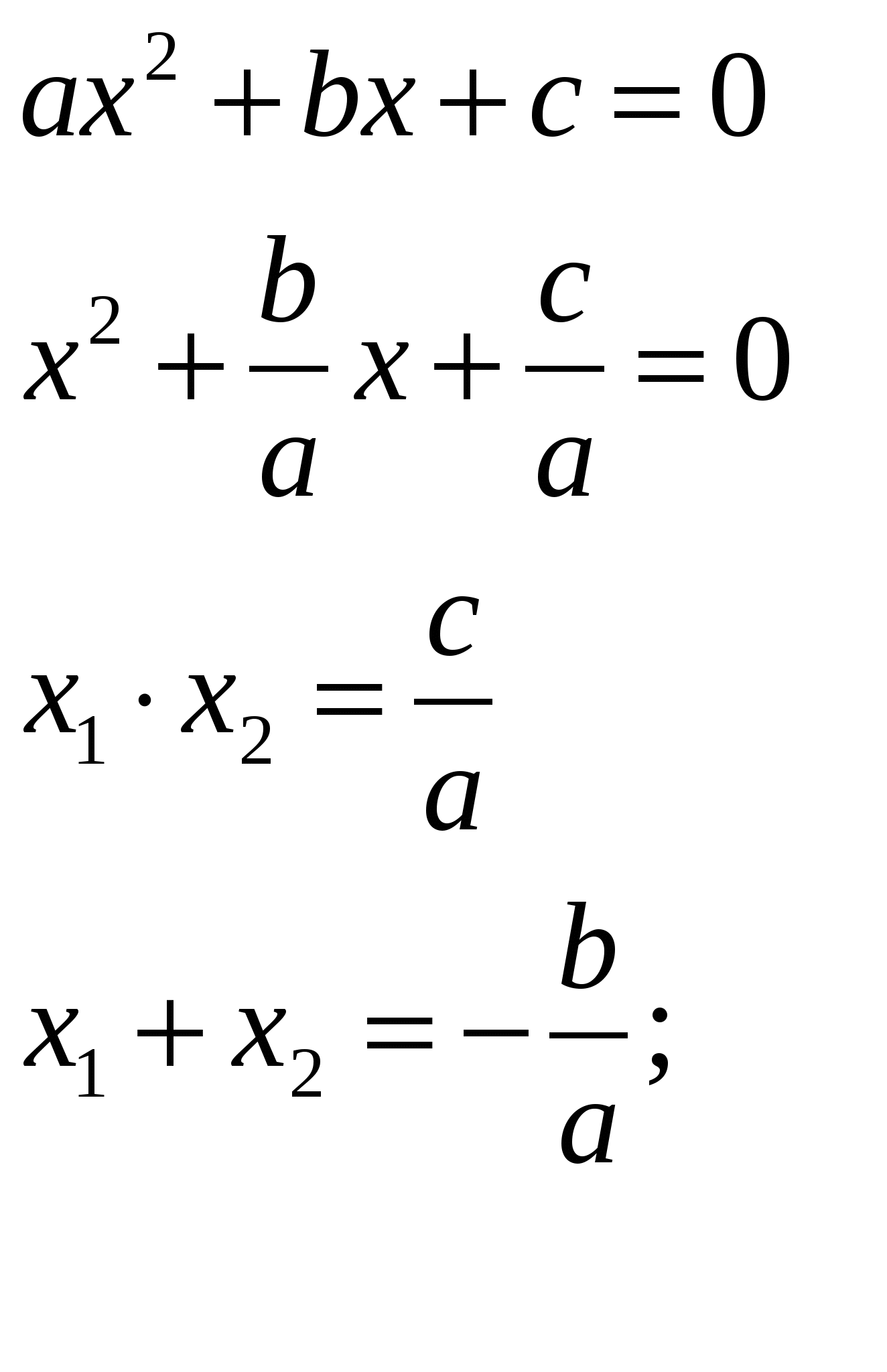
По праву достойна в стихах быть воспета

О свойствах корней теорема Виета

Что лучше, скажи постоянства такого

Умножишь ты корни - и дробь уж готова?

В числителе с, в знаменателе а,

А сумма корней тоже дроби равна

Хоть с минусом дробь, что за беда!

В числителе b, в знаменателе а

Теорема (обратная теореме Виета).

Если числа х₁ и х₂ таковы, что x₁ + x₂ = - p, x1 ∙ x2 = q, то эти числа являются корнями уравнения x² + px + q = 0.

Устно: 1)Правильно ли найдены корни квадратного уравнения:

1) х² - 6х + 5 = 0,

х₁= 1, х₂ = 5;

2) х² + 3х - 40 = 0,

х₁= - 8, х₂ = 5;

3) х² - 2х - 3 = 0,

х₁ = - 1, х₂=3;

2)Составить приведенное квадратное уравнение, если x₁ = -3, x₂ = 1:

x₁ + x₂ = -3 + 1 = 2

x₁ · x₂ = -3 · 1 = -3

p = -2; q = -3

x² + px + q = 0

x² + 2x - 3 = 0

Составьте приведенное квадратное уравнение, если его корни равны:

а) х₁ = - 3, х₂ = -2;

б) х₁= - 3, х₂= - 4;

в) х₁ = 5, х₂ = 6.

3)В уравнении х² + pх + 36 = 0 один из корней равен - 4. Найдите другой корень и коэффициент p.

Вернёмся к уравнению х² - 2008х + 2007 = 0. Найдём его корни.

Первичная проверка знаний ( с последующей взаимопроверкой):

Вариант 1

1)Cоставить приведенное квадратное уравнение

x₁ = 5, x₂ = 6

2) Правильно ли найдены корни квадратного уравнения:

х² - 16х + 63 = 0

x₁ = 7, x₂ = 9

3) Один из корней квадратного уравнения равен -3. Найти коэффициент р и второй корень уравнения:

х² + рх + 18 = 0.

Вариант 2

1)Cоставить приведенное квадратное уравнение

x₁ = - 5, x₂ = 6

2) Правильно ли найдены корни квадратного уравнения:

х² + 18х - 63 = 0

x₁ = -21, x₂ = 3

3) Один из корней квадратного уравнения равен -2. Найти коэффициент р и второй корень уравнения:

х² + рх - 16 = 0.

Подведение итогов урока, запись домашнего задания, рефлексия.

Рефлексия.

Сегодня на уроке я узнал …

Сегодня на уроке я научился …

На следующих уроках мне хотелось бы…