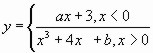Практическая работа в 10 классе по теме «Производная»

Предмет: Алгебра и начала анализа

Класс: 10

Название раздела: Производная

Цели урока:

1. Обобщить и систематизировать сведения о нахождении производной функции, повторить алгоритм нахождения производной функции по определению.

2. Закрепить навыки нахождения производной функции по правилам и по таблице производных

3. Развивать навыки исследования, коллективной работы, с использованием различной форм контроля и оценки.

Оборудование: Раздаточный материал.

Тип урока: Обобщающий урок по теме.

Ход урока: В начале занятия каждый ученик получает раздаточный материал, согласно содержания, которого осуществляется дальнейшая работа.

Практическая работа по теме

«Производная»

Учебный элемент интегрирующая цель

Учебный элемент 1 входной контроль

Учебный элемент 2 нахождение приращения функции и производной функции по определению

Учебный элемент 3 нахождение производной функции по правилам и по таблице производных

Учебный элемент 4 нахождение производной сложной функции

Учебный элемент 5 физический смысл производной функции

Учебный элемент 6 непрерывность и дифференцируемость функции

Учебный элемент 7 выходной контроль

Интегрирующая цель

1. Обобщить и систематизировать сведения о нахождении производной функции, повторить алгоритм нахождения производной функции по определению.

2. Закрепить навыки нахождения производной функции по правилам и по таблице производных.

3. Развивать навыки исследования, коллективной работы, с использованием различной форм контроля и оценки.

Входной контроль

1.1 Верны ли утверждения:

а);

б) если функция дифференцируема в точке, то она непрерывна в этой точке;

в) если функция непрерывна в точке, то она дифференцируема в этой точке;

г) если d(X)-> 0, то d(Y)-> 0;

д) (f(x)g(x))' =f'(x)g'(x);

е) n _мгнов=s'(t);

Работаем 2 минуты, контроль по устному ответу ученика

1.2 Найдите производную функции и укажите, какое правило вы использовали

а) ;

б) y= arcsinx;

в) y=;

г) y=tg2x;

д);

е) y=x sinx;

ж).

Работаем 8 минут, контроль по устному ответу ученика

Нахождение производной функции по определению

Цель: Проверить знание алгоритма нахождения производной в точке и умение его применять

2.1 Найдите приращение функции в точке х₀

y=-3x²-13x y=7x²+3x

2.2 Приведите алгоритм нахождения производной

1.
2.
3.
4.

2.3 Используя алгоритм, найдите производную функции в точке х₀

Вернитесь к цели УЭ2 . Достигнута ли она? Если у вас возникли вопросы, можете задать их учителю. Если вопросов нет, переходите к следующему заданию

Работаем 4 минуты, контроль по ответу у доски

Работаем 5 минут

Контроль на доске

Нахождение производной функции по правилам и по таблице производных

Цель: закрепить навыки нахождения производной функции по правилам дифференцирования и по таблице производных.

3.1 Найдите производную функции

а) y=x⁵+9x²⁰+1; y=x⁷-4x¹⁶-3;

б) Y=(x²-1)(x⁴+2); y=(x²-2)(x⁷+4);

в); ;

г) y=; ;

3.2 Найдите значение производной функции в точке х₀

y=-4tgx y=ctgx-2

х₀ =0 х₀ =-p /6

3.3 Решите неравенство

f'(x)>0, если f'(x)<0, если

3.4 При каких значениях х выполняется неравенство?

f'(x)=2 f'(x)=1

f(x)=2x-5x²+3p² f(x)=3x-arctg0,7+x²

Вернитесь к цели УЭ3, если вам все понятно, то продолжайте работу дальше

Работаем 7 минут, контроль в парах

Работаем 2 минуты, контроль по устному ответу ученика

Работаем 6 минут. Контроль в парах

Работаем 2 минуты, контроль по ответу у доски

Нахождение производной сложной функции

Цель: проверяем знание теоремы о дифференцируемости сложной функции и умение ее применять

4.1 Найдите производную функции

а) y=sin(x/2)

б)

в)

г) y=sin³ (2x³)

4.2 Решите неравенство

а) y'>0

б) y'<0

Вернитесь к цели УЭ4, если вы все поняли, то продолжайте работу дальше, если нет, обратитесь к учителю

Работаем 10 минут, контроль на доске

Работаем 5 минут. Контроль у учителя

Физический смысл производной функции

Цель: Вы должны иметь четкое представление о том, что скорость есть производная от пути по времени, а ускорение есть производная скорости по времени

5.1 Материальная точка движется прямолинейно по закону .

а) выведите формулу для вычисления скорости движения в любой момент времени t

б) найдите скорость в момент времени t=2 с

в) через сколько секунд после начала движения точка остановится

5.2 Точка движется прямолинейно по закону S(t)=2t³+t-1, в какой момент времени ускорение будет равно 2?

5.3 По прямой движутся две материальные точки по законам S(t)=4t² -3; S(t)=t³ . В каком промежутке времени скорость первой точки больше скорости второй точки

Вернитесь к цели У-Э-5. Достигли ли вы этой цели? Продолжайте работу дальше

Работаем 10 минут, контроль по устному ответу ученика

Непрерывность и дифференцируемость

6.1 Является ли функция непрерывной в точке х=0?

6.2 При каком значении m функция непрерывна в т х₀=2?

6.3 При каких значениях параметров a и b функция

а) непрерывна в т. х=0?

б) дифференцируема в т. х=0?

Работаем 6 минуты, контроль в парах

Работаем 10 минут, контроль по образцу

Выходной контроль

(подсчитайте количество баллов n, если n>75, то вы молодец и решаете задания второго уровня сложности. Если же n<75, не отчаивайтесь, еще немного усердия и все получится. А сейчас приступайте к выполнению заданий первого уровня сложности)

Уровень 1

1) Найдите производную функции

2) Докажите, что функция непрерывна в точке х=-2, но не дифференцируема в этой точке.

Уровень2

1)Найдите производную функции

2) Решите уравнение: f? (x)=0

f(x)=

3) При каких значениях параметров a и b функция