- Учителю
- Научная работа по математике Первообразная и её свойства. Неопределённый интеграл, его свойства.
Научная работа по математике Первообразная и её свойства. Неопределённый интеграл, его свойства.
Содержание
Введение……………………………………………………………………………2
-
Первообразная и её свойства. Неопределённый интеграл, его свойства. Основные правила интегрирования………………………………………………………….3
-
Замена переменной в неопределённом интеграле. Интегрирование по частям. Циклический интеграл…………………………………………………………….5
-
Интегрирование рациональных дробей…………………………………………..7
-
Интегрирование тригонометрических функций…………………………………11
-
Интегрирование иррациональностей…………………………………………….12
-
Приближённое вычисление определённого интеграла…………………………14
-
Определённый интеграл. Свойства определённого интеграла………………...16
-
Вычисление площадей плоской области…………………………………………18
-
Длина дуги кривой…………………………………………………………………21
-
Несобственные интегралы……………………………………………………….24
Заключение………………………………………………………………………..27
Тест…………………………………………………………………………………28
Ключ к тесту……………………………………………………………………….67
Список используемой литературы………………………………………………71
Введение
Интегральное исчисление является важнейшим разделом математического анализа, его методы - одни из основных инструментов решения прикладных задач в математике, физике, экономике и других научных областей. Интегрирование - это настоящее искусство, ему можно научиться лишь глубоко изучив теорию и решив достаточное количество упражнений. Как раз освоение простейших приёмов, используемых в интегрировании, можно проверить с помощью решения тестовых заданий.
В курсовой работе по каждому из основных разделов интегрального исчисления приведены краткие теоретические сведения, позволяющие ответить на базовые теоретические вопросы и получить решения несложных практических задач. Пункты 1-10 содержат основные формулы, используемые при интегрировании неопределённых, определённых и несобственных интегралов, а также при вычислении некоторых геометрических величин.
Тест, включённый в текст курсовой работы, состоит из ста заданий, распределённых по темам и снабжённых решениями и четырьмя вариантами ответов. После тестовых заданий даётся ключ к тесту.
-
Первообразная и её свойства. Неопределённый интеграл, его свойства. Основные правила интегрирования.
Эти понятия связаны с задачей отыскания функции по известной её производной.
Определение. Функция F(x) на данном промежутке X
называется первообразной для функции f(x) (или интегралом для
f(x))), если для всех x промежутка X функция f(x) является
производной функции F(x), то есть ![]()
Теорема. Если на промежутке X функция F(x) является первообразной для f(x), то и функция F(x)+С, где С=const, также будет первообразной для f(x).
Действительно, пусть F(x) - первообразная для f(x) и С=const. Составим функцию Ф(x)=f(x)+C. Её производная Ф'(x)=(F(x)+C)'=F'(x)+0=f(x), то есть, по определению, функция Ф(х)=F(x)+C является первообразной.
Операция отыскания первообразной называется
интегрированием и обозначается ![]() (1)
(1)
где f(x) - подынтегральная функция, f(x)dx - подынтегральное выражение, dx - дифференциал аргумента (указывающий, по какой переменной производится интегрирование).
Свойства неопределённого интеграла и простейшие правила интегрирования
-
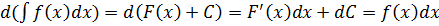
-
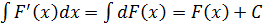
-
(
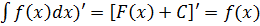
-
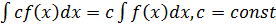
-
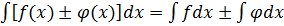
-
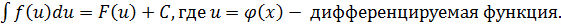
Последние три свойства относятся к правилам интегрирования.
Первые три свойства устанавливают связь операций дифференцирования и интегрирования как взаимообратных и взаимопроверяемых.
Таблица интегралов
-
Метод замены переменной (или подстановки)
Теорема. Если 1. функция x=φ(t) монотонна дифференцируема на (α, β),
2. функция f(x) непрерывна на [а, б], то
![]() (1)
(1)
Доказательство. Продифференцируем (1) по x,
используя: свойство 3 неопределённого интеграла и известные формулы
дифференцирования сложной и обратной функции: ![]() ,
, ![]()
Тогда производная левой части формулы (1):
![]()
Производная правой части:
![]() (t))
(t))![]() .
.
![]()
Интегрирование по частям
Пусть u(x), v(x) - функции, имеющие непрерывные производные.
Тогда ![]() Используя свойства 2 и 5 неопределённого интеграла, интегрируем
последнее равенство:
Используя свойства 2 и 5 неопределённого интеграла, интегрируем
последнее равенство:
![]() (2)
(2)
(2) - формула интегрирования по частям.
Замечание 1. Разбивая подынтегральное выражение на множители u, dv необходимо придерживаться двух правил:
Интегрирование дифференциала не должно представлять трудностей;
Применение формулы должно привести к упрощению подынтегральной функции (приблизить её к табличному виду)
Замечание 2. Если аргументы функции и дифференциала не совпадают, то лучше предварительно упростить подынтегральное выражение.
Замечание 3. Для интегралов вида:
![]()
(в частности, степенная функция xn ), f(x)=eax, sin ax, cos ax, ln x, arctg x, arcsin x, …, применяют интегрирование по частям, причем в большинстве случаев легко интегрируемые выражения: sin x dx, cos x dx, ex dx обозначают dv, а множитель при них P(x)=u; и наоборот, если f(x)=ln x, arcsin x, arctg x, то эту функцию обозначают u(x), а оставшуюся часть подынтегрального выражения - dv.
Замечание 4. А) Интегралы ![]() называются циклическими, так как в процессе применения (2)
подынтегральная функция принимает первоначальный вид.
называются циклическими, так как в процессе применения (2)
подынтегральная функция принимает первоначальный вид.
Применим к первому из них формулу (2).
Обозначим:
![]()
![]()
![]()
,
, ![]()
![]()
![]()
![]()
![]()
,
![]()
![]() .
.![]() (3)
(3)
б) По такому же принципу можно найти интеграл
типа ![]() , где k целое число, k > 1 .
, где k целое число, k > 1 .
![]()
![]()
![]() ,
,
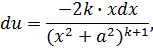
![]()
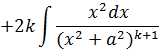
Последний интеграл преобразуем в сумму интегралов:
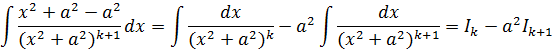
В итоге имеем:
![]()
.Получаем формулу, понижающую порядок k:
![]() (4)
(4)
Формула (4) является так называемой рекуррентной формулой, в которой последующий интеграл вычисляется через предыдущий.
-
Интегрирование рациональных дробей
Определение.
Дробь ![]() называется рациональной, если
называется рациональной, если ![]() многочлены целой степени.
многочлены целой степени.
![]()
Причём если m<n, то дробь называется правильной.
Теорема 1. Уравнение ![]() имеет ровно n корней, действительных или комплексных (включая их
кратность), причём каждый комплексный корень (a+bi) имеет
сопряжённый (a-bi).
имеет ровно n корней, действительных или комплексных (включая их
кратность), причём каждый комплексный корень (a+bi) имеет
сопряжённый (a-bi).
Теорема 2. Каждый целый многочлен с вещественными коэффициентами разлагается, и притом единственным образом, на вещественные множители
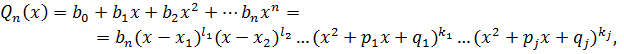
где ![]() кратность действительных корней
кратность действительных корней ![]() ,
,
![]() кратность
комплексных корней,
кратность
комплексных корней,
![]()
Паре сопряжённых комплексных корней ![]() соответствует квадратный трёхчлен
соответствует квадратный трёхчлен ![]()
Теорема 3. Каждая правильная дробь может быть представлена в виде суммы конечного числа простых дробей вида
![]()
Проинтегрируем каждую из простых дробей:
![]()
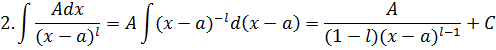
![]()
![]()
Последние два интеграла предварительно преобразуем: в знаменателе выделим полный квадрат:
![]()
(по условию знаменатель не имеет действительных
корней - ![]()
![]() ).
).
Положим: ![]()
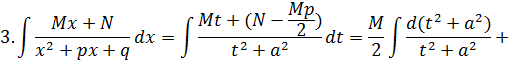
![]()
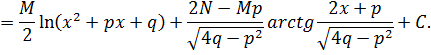
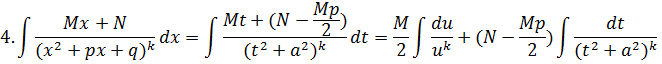 Итак,
правильная рациональная дробь может быть представлена в виде:
Итак,
правильная рациональная дробь может быть представлена в виде:
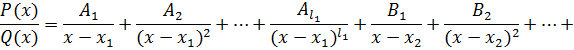
![]() (1)
(1)
Линейному множителю в знаменателе соответствует одночлен в числителе, квадратному множителю в знаменателе - двучлен в числителе.
Числа ![]() находим методом неопределённых коэффициентов. В правой части
равенства все дроби приводим к общему знаменателю - это Q(x).
Остаётся приравнять числители левой и правой частей, но так как это
многочлены, то надо приравнять коэффициенты при одинаковых
степенях. Получим систему линейных уравнений, которая всегда
совместна и определена.
находим методом неопределённых коэффициентов. В правой части
равенства все дроби приводим к общему знаменателю - это Q(x).
Остаётся приравнять числители левой и правой частей, но так как это
многочлены, то надо приравнять коэффициенты при одинаковых
степенях. Получим систему линейных уравнений, которая всегда
совместна и определена.
Правила интегрирования рациональных дробей
-
Установить: дробь рациональная, правильная или неправильная. Если неправильная - выделить целую часть.
-
Найти корни знаменателя и записать его в виде произведения множителей (по теореме 2).
-
Правильную дробь разложить на сумму простых дробей:
Вид знаменателя: ![]() , число простых дробей p, вид дробей:
, число простых дробей p, вид дробей:
![]()
Вид знаменателя: ![]() , число простых дробей l, вид дробей:
, число простых дробей l, вид дробей:
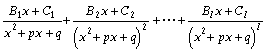
-
Найти коэффициенты.
-
Проинтегрировать.
-
Интегрирование тригонометрических функций
R(sin x, cos x)
Универсальная подстановка ![]() сводит рациональную функцию R(sin x, cos x) к рациональной дроби,
интегрирование которой рассмотрено в предыдущем пункте.
сводит рациональную функцию R(sin x, cos x) к рациональной дроби,
интегрирование которой рассмотрено в предыдущем пункте.
Выведем формулы для замены sin x, cos x:
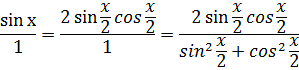
Заменяем числитель и знаменатель на ![]()
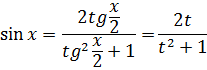
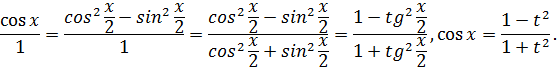
Из подстановки явно выделим x:
![]()
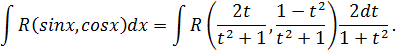
-
Интегрирование иррациональностей
![]() где
R - рациональная функция своих аргументов,
где
R - рациональная функция своих аргументов,
![]() целые
числа.
целые
числа.
Подстановка ![]() - общий знаменатель всех дробей
- общий знаменатель всех дробей ![]() рационализирует подынтегральную функцию.
рационализирует подынтегральную функцию.
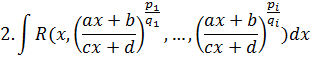
Пусть q - общий знаменатель всех дробей
![]() тогда подстановка
тогда подстановка ![]() рационализирует подынтегральную функцию.
рационализирует подынтегральную функцию.
![]() рациональные
числа.
рациональные
числа.
Подынтегральное выражение носит название
дифференциального бинома и интегрируется в конечном видом только в
трёх случаях - если целым оказывается одно из чисел: p, ![]()
Эти случаи интегрируемости были известны ещё Ньютону, но только в середине 19 века Чебышев установил замечательный факт, что других случаев интегрируемости в конечном виде для биномиальных дифференциалов не существует.
Замечание. В некоторых частных видах иррациональных функций, содержащих квадратные корни из суммы или разности квадратов, удобно использовать тригонометрические функции:
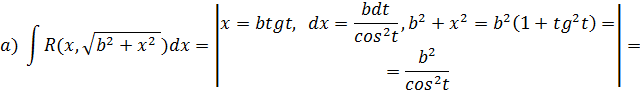
![]()
![]()
![]()
-
Приближенное вычисление определённого интеграла
1. Формула прямоугольников.</</span>
Разделим отрезок ![]() точками
точками ![]() на nравных частей. Длина каждого отрезка
на nравных частей. Длина каждого отрезка ![]() Построим прямоугольники с основаниями
Построим прямоугольники с основаниями ![]() и высотой
и высотой ![]()
Тогда площадь криволинейной трапеции приближённо будет равна сумме площадей построенных прямоугольников
![]()
-
Формула трапеции
Разделим отрезок ![]() точками
точками ![]() на n равных частей и построим трапеции, заменив дугу кривой
хордой, с основаниями
на n равных частей и построим трапеции, заменив дугу кривой
хордой, с основаниями ![]()
Высоты у них равны ![]() . Площадь каждой трапеции вычисляется по известной формуле
(полусумму оснований умножить на высоту).
. Площадь каждой трапеции вычисляется по известной формуле
(полусумму оснований умножить на высоту).
![]()
![]()
Искомая площадь приближённо равна сумме площадей построенных трапеций:
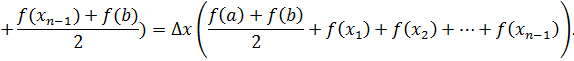
![]() (1)
(1)
Это и есть формула трапеций.
-
Параболическая формула или формула Симпсона
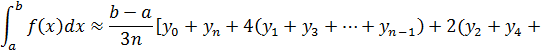
![]() (2)
(2)
(n-чётное число).
Формула (2) чаще других используется для приближённых вычислений, так как даёт более точный ответ при тех же затратах труда. Точность можно улучшать, увеличивая число делений.
Формулу (2) иногда записывают в несколько ином виде (для чётного числа разбиений n=2k):
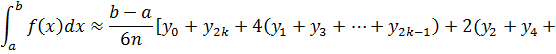
![]()
-
Определённый интеграл
Свойства определённого интеграла
1.![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7.![]()
8. ![]()
9. Теорема об оценке определённого интеграла.
Если функция f(x) непрерывна на ![]() , m и M соответственно её наименьшее и наибольшее значения на
, m и M соответственно её наименьшее и наибольшее значения на
![]() , то
, то
![]() .
.
-
Теорема о среднем.
-
Если функция f(x) непрерывна на
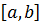 ,то найдётся точка
,то найдётся точка 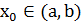 такая, что
такая, что 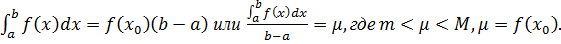
11.Пусть ![]() . Рассмотрим определённый интеграл как функцию верхнего п
. Рассмотрим определённый интеграл как функцию верхнего п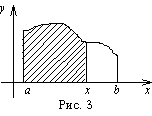 редела
редела
![]()
Геометрически это переменная площадь:
Теорема.
Производная от определённого интеграла с
переменным верхним пределом по переменному пределу равна
подынтегральной функции ![]()
12.Основная формула интегрального исчисления или теорема Ньютона-Лейбница.
![]()
Замена переменной в определённом интеграле
Пусть f(x) непрерывна на ![]() и функция
и функция ![]() монотонна и дифференцируема на (a, b), причём
монотонна и дифференцируема на (a, b), причём ![]() Тогда
Тогда ![]()
Интегрирование по частям в определённом интеграле
Пусть u(x), v(x) дифференцируемы и интегрируемы на ![]() . Тогда
. Тогда
![]() (2)
(2)
-
Вычисление площадей с помощью определённого интеграла в декартовой системе координат
Рассмотрим различные варианты расположения областей.
1.Пусть криволинейная трапеция ограничена кривой
![]() осью Ox и прямыми x=a, x=b. Её площадь равна:
осью Ox и прямыми x=a, x=b. Её площадь равна: ![]()
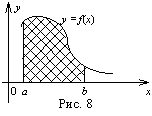
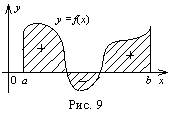
2.Пусть ![]() конечное число раз меняет знак на отрезке
конечное число раз меняет знак на отрезке ![]() . По свойству 6 интеграл по всему отрезку
. По свойству 6 интеграл по всему отрезку ![]() равен сумме интегралов по составляющим отрезкам. Площадь равна
сумме абсолютных величин интегралов по каждому из отрезков, то есть
равен сумме интегралов по составляющим отрезкам. Площадь равна
сумме абсолютных величин интегралов по каждому из отрезков, то есть
![]() .
.
3.Площадь фигуры, ограниченной кривыми ![]() и прямыми x=a, x=b, находим по формуле:
и прямыми x=a, x=b, находим по формуле:
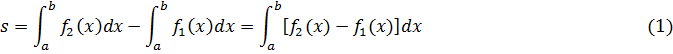
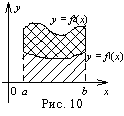
4.Площадь трапеции, основанием которой является ось ординат , удобнее вычислять по формуле
![]()
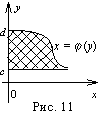 dy
dy
5. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме:
![]() (2)
(2)
Данные параметрические уравнения определяют
некоторую функцию y=f(x) на отрезке ![]() и, следовательно, можно воспользоваться основной формулой
и, следовательно, можно воспользоваться основной формулой
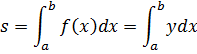
Перейдём в этом интеграле к переменной t по формулам (2):
![]()
Найдём пределы изменения новой переменной: если
![]() то переменная t изменяется от
то переменная t изменяется от ![]() при условии, что
при условии, что ![]()
Выполнив указанную подстановку, получим формулу для вычисления площади криволинейной трипеции, ограниченной параметрически заданной кривой:
![]() (3)
(3)
-
Длина дуги кривой
Длина дуги кривой в прямоугольных координатах
Найдём длину дуги АВ кривой ![]() , где А(а,f(a)), B
, где А(а,f(a)), B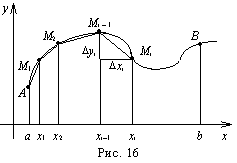 (b,f(b)).
(b,f(b)).
Длиной дуги называется предел, к которому стремится длина вписанной ломаной линии при условии, что число звеньев неограниченно возрастает и длина наибольшего из них стремится к нулю.
![]() длина
звена Мi-1Mi ломаной АВ.
длина
звена Мi-1Mi ломаной АВ.
Рассмотрим незамкнутую дугу АВ, заданную уравнением y=f(x).
Пусть f(x) и ![]() непрерывны на
непрерывны на ![]() . Разобьём дугу АВ на n частей произвольным образом точками
. Разобьём дугу АВ на n частей произвольным образом точками
![]()
Длина i-того звена ![]() равна длине вектора
равна длине вектора ![]() .
.
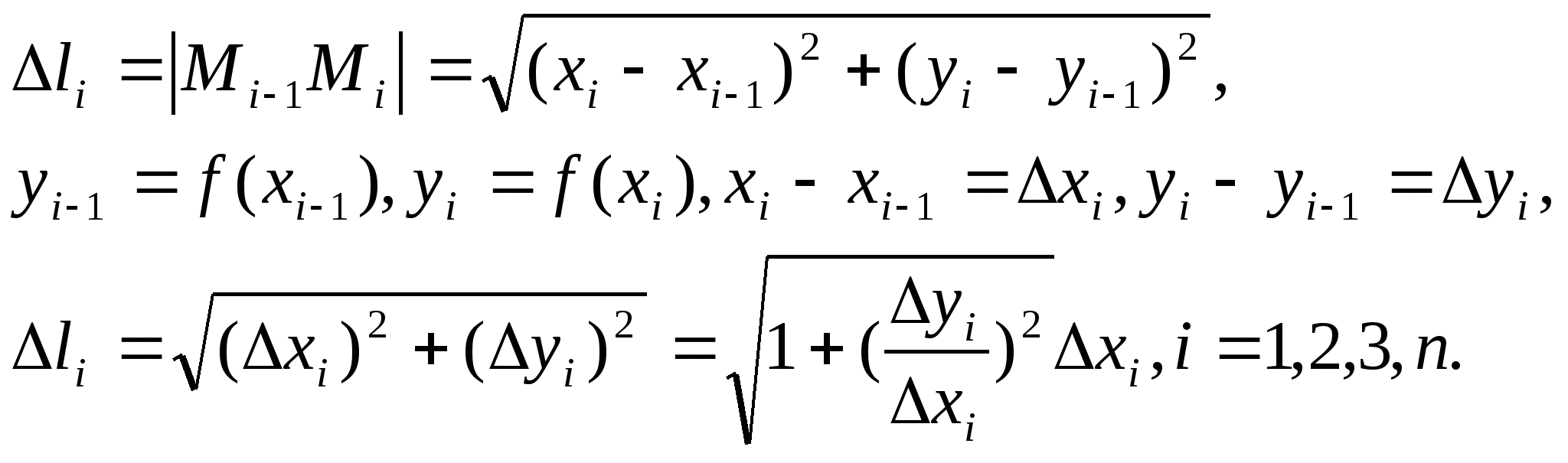
По теореме Лагранжа на отрезке ![]() существует такая точка
существует такая точка ![]() что
что ![]() то есть
то есть ![]()
Просуммировав все ![]() , получим приближённое значение длины дуги АВ:
, получим приближённое значение длины дуги АВ:
![]()
Перейдя к пределу при ![]() и
и ![]() , получим точное значение длины дуги.
, получим точное значение длины дуги.
![]()
В правой части равенства предел интегральной суммы существует в силу непрерывности функции f(x) и её производной и не зависит от способа разбиения дуги на части.
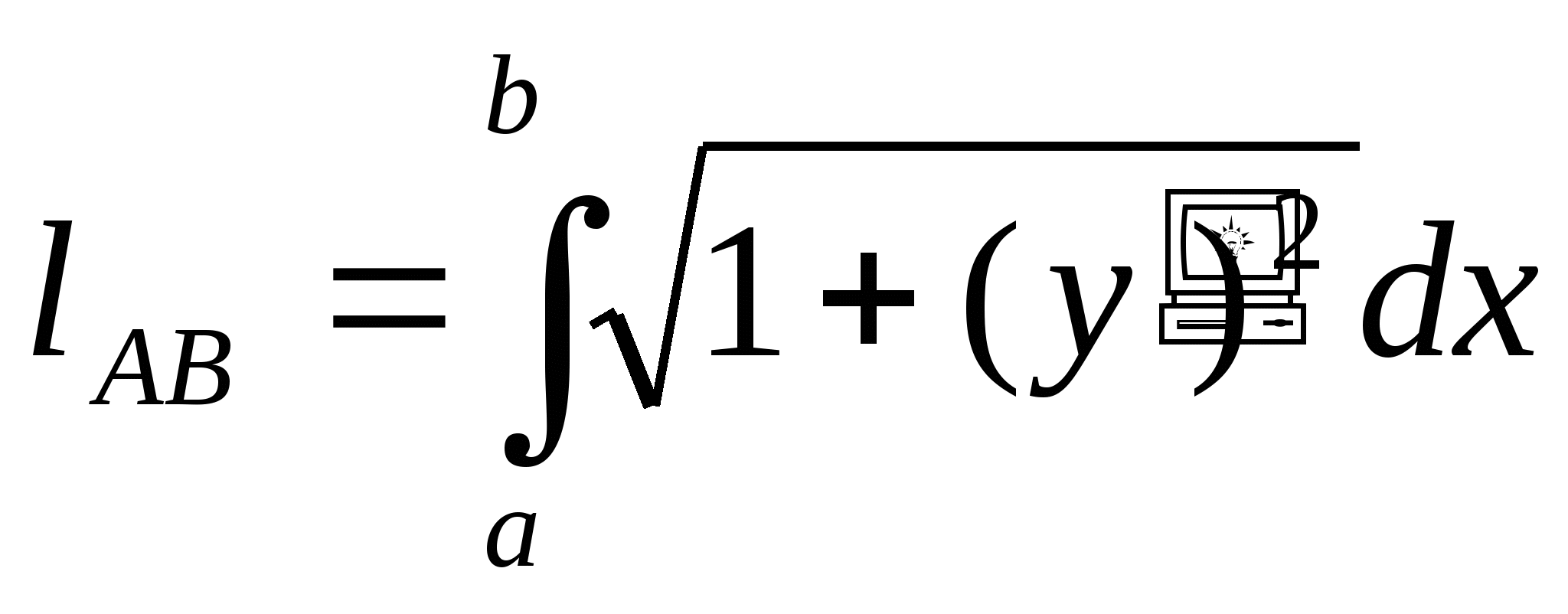
Длина дуги кривой, заданной параметрически
Пусть теперь кривая АВ задана параметрическими уравнениями
![]() (*)
(*)
Где функции ![]() непрерывны вместе со своими производными, причём
непрерывны вместе со своими производными, причём ![]()
Преобразуем формулу 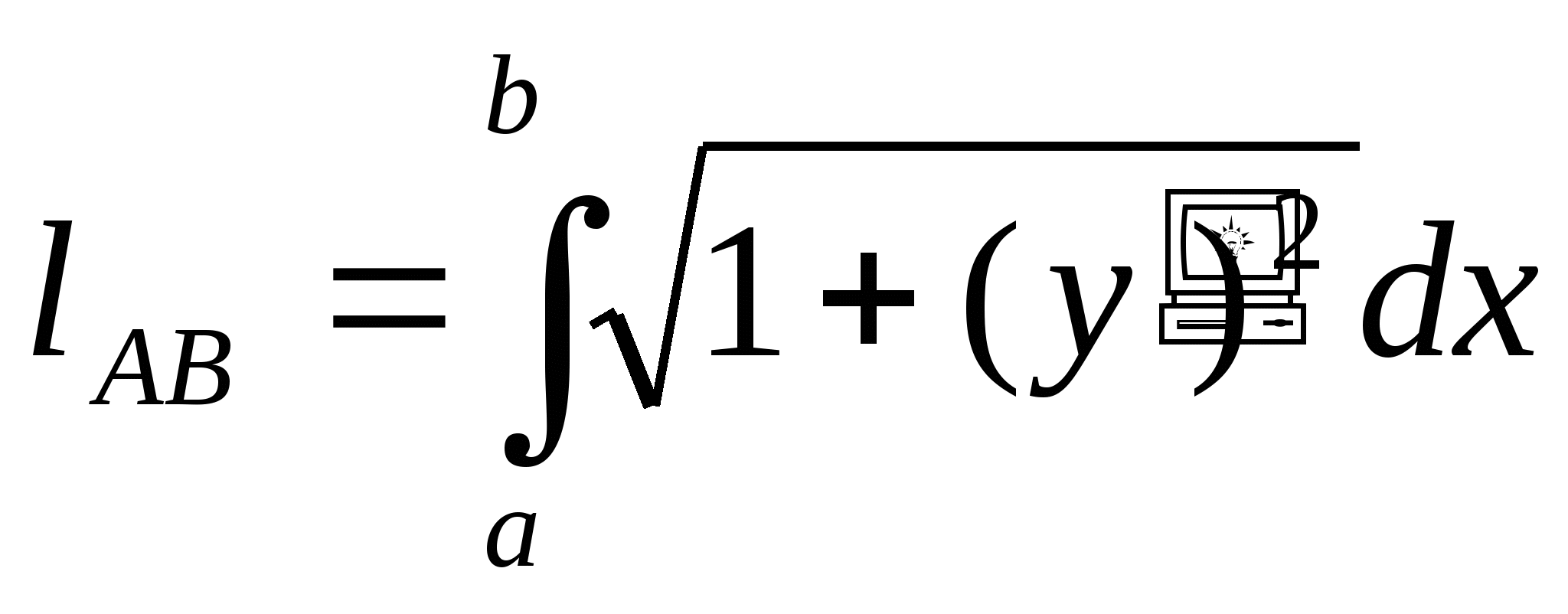 , выполнив замену переменной по уравнениям (*).
, выполнив замену переменной по уравнениям (*).
Пусть ![]()
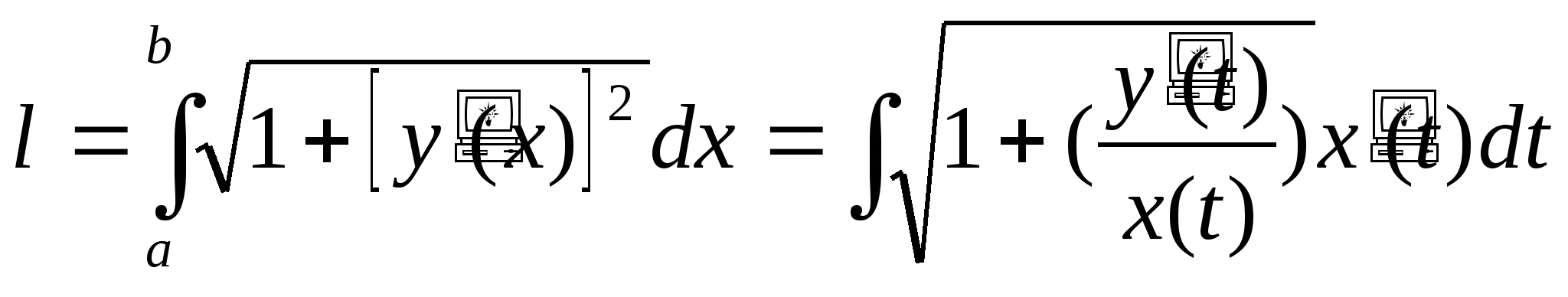
Отсюда следует формула для вычисления длины дуги, заданной параметрически:
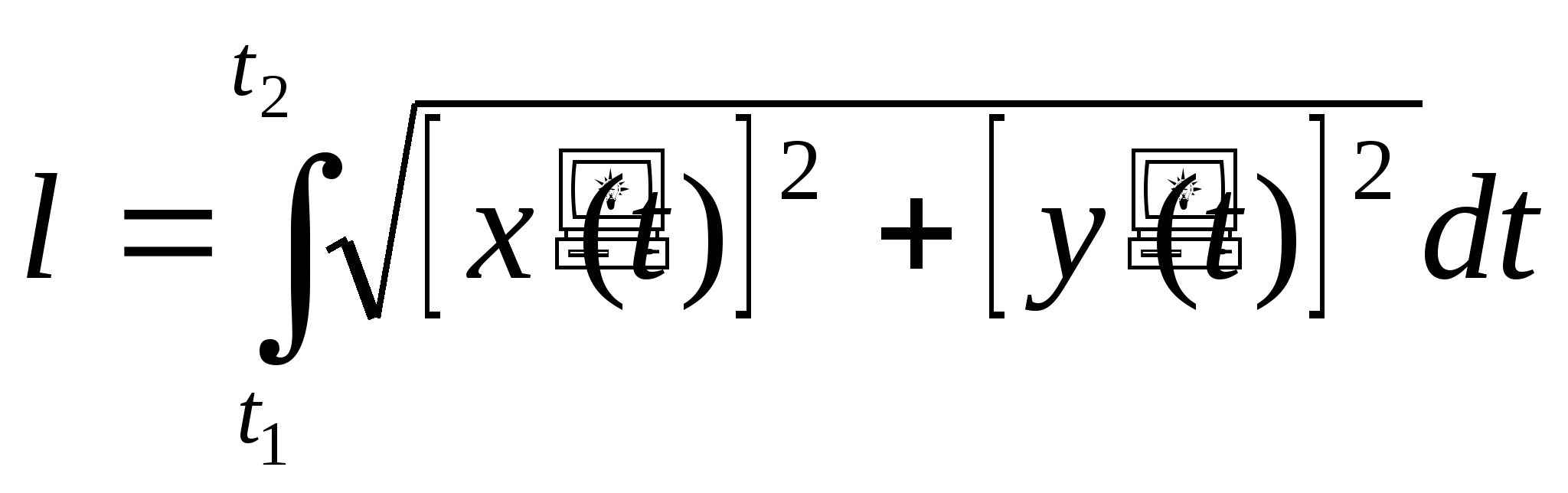
Длина дуги кривой в полярной системе координат
Пусть уравнение кривой задано в полярной системе
координат: ![]()
Преобразуем формулу 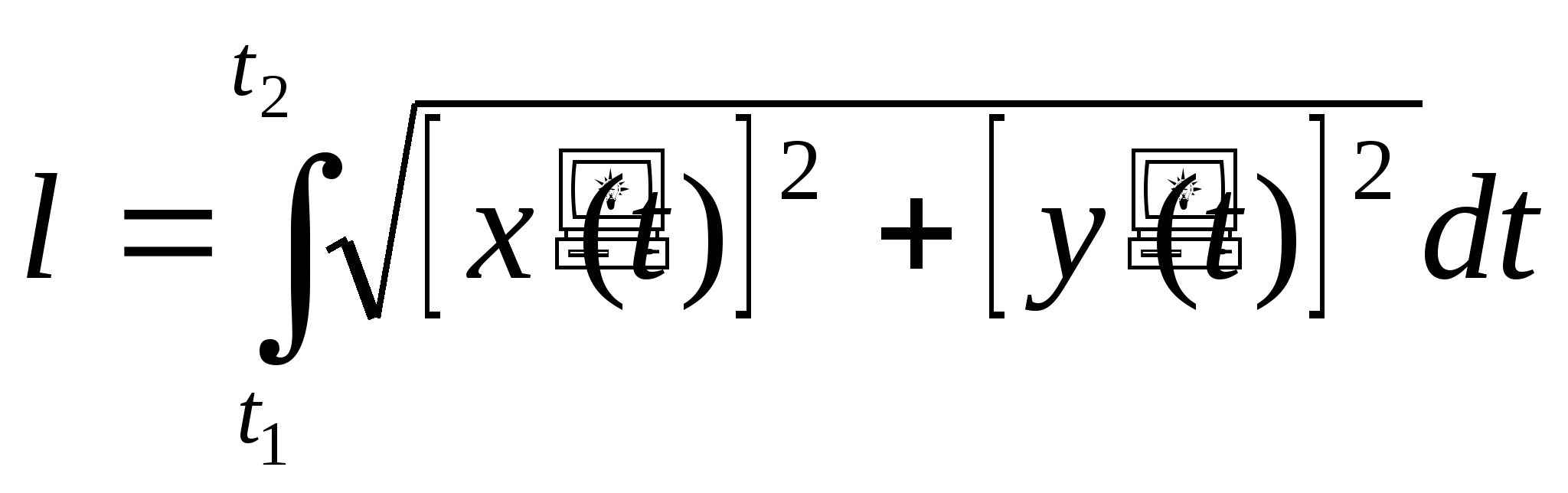 , рассматривая угол
, рассматривая угол ![]() в качестве параметра. Воспользуемся обычными формулами перехода от
декартовых координат к полярным:
в качестве параметра. Воспользуемся обычными формулами перехода от
декартовых координат к полярным:
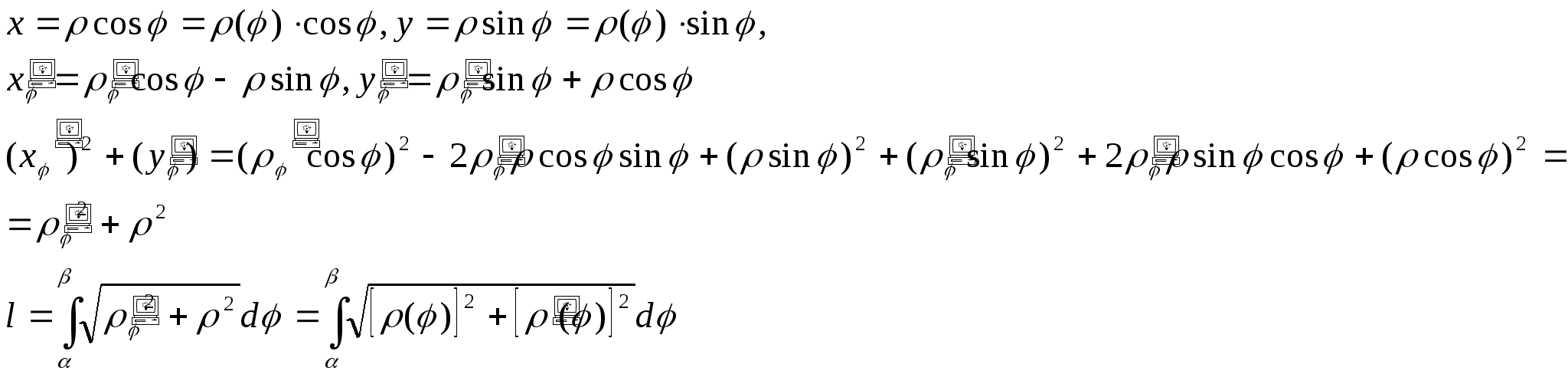
Получили формулу для вычисления длины дуги кривой в полярной системе координат.
-
Несобственные интегралы
Понятие определённого интеграла определено для конечного интервала и непрерывной на нём функции. Распространим это понятие на случаи бесконечного интервала интегрирования и разрывной функции.
Интеграл с бесконечными пределами
Пусть функция f(x)определена и непрерывна при
всех значениях ![]() .
.
Рассмотрим интеграл 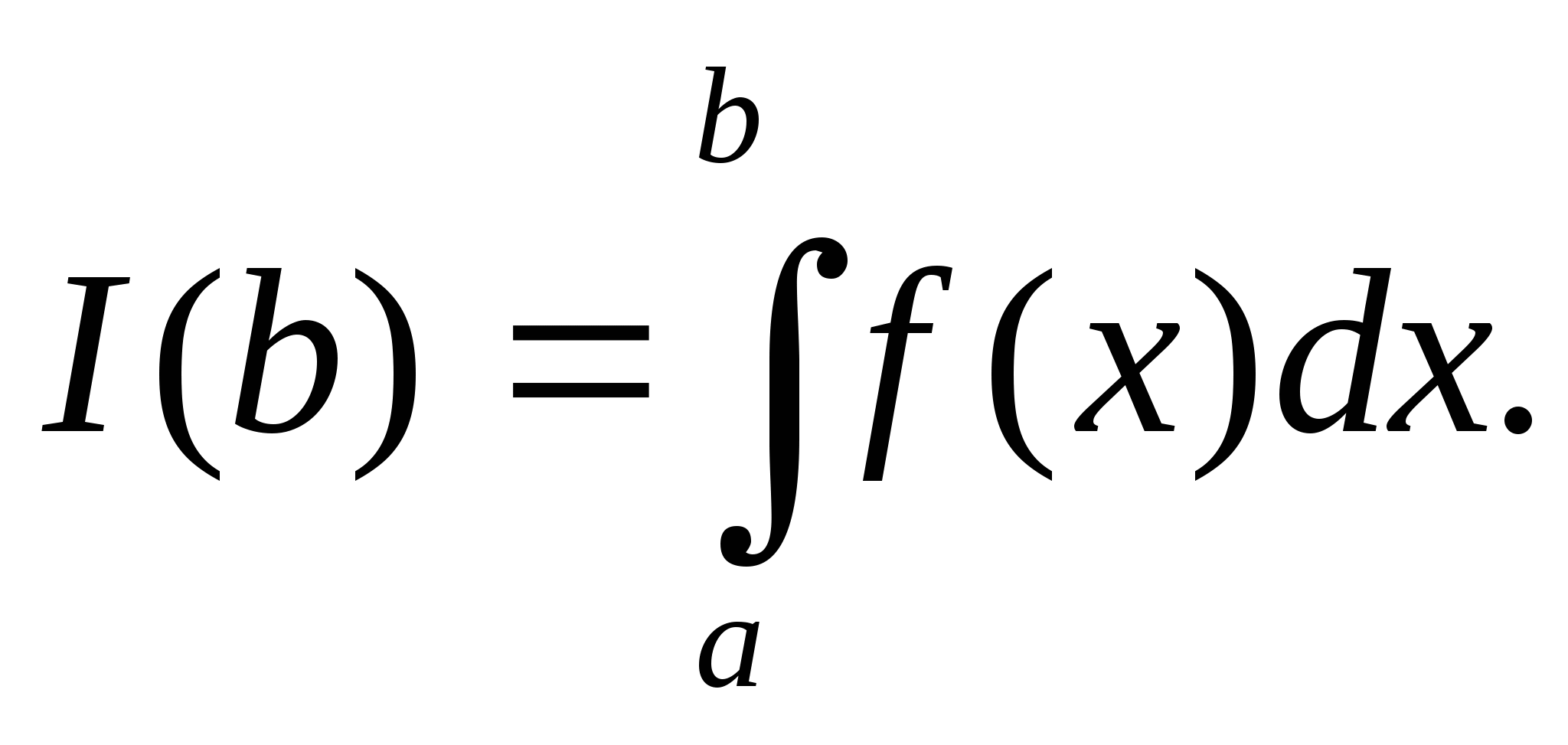 Он имеет смысл при любом b>a .При изменении b интеграл
изменяется, являясь непрерывной функцией . Пусть
Он имеет смысл при любом b>a .При изменении b интеграл
изменяется, являясь непрерывной функцией . Пусть ![]() .
.
Определение. Несобственным интегралом от функции
f(x) в интервале ![]() называется предел интеграла
называется предел интеграла 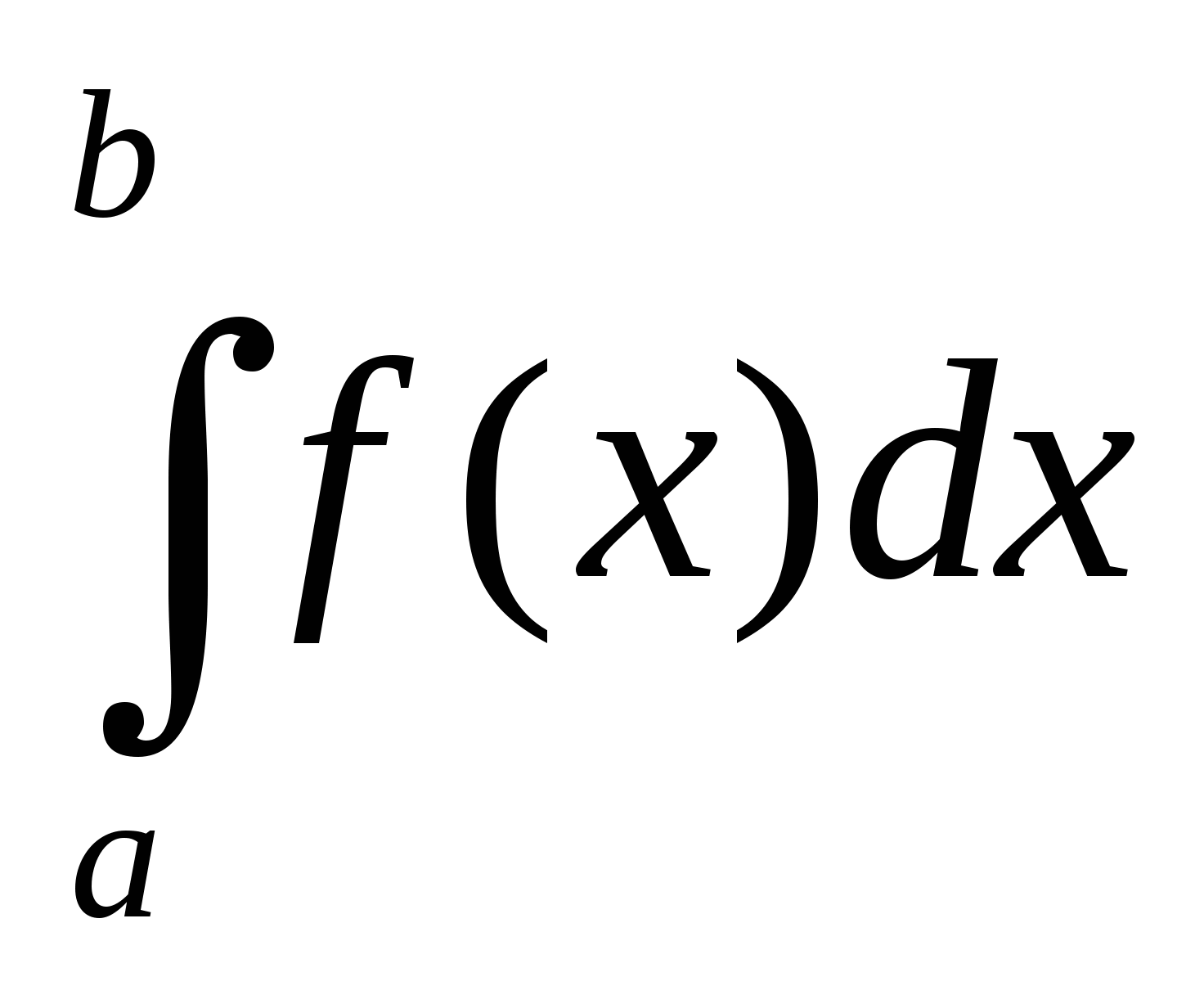 при
при ![]() :
:
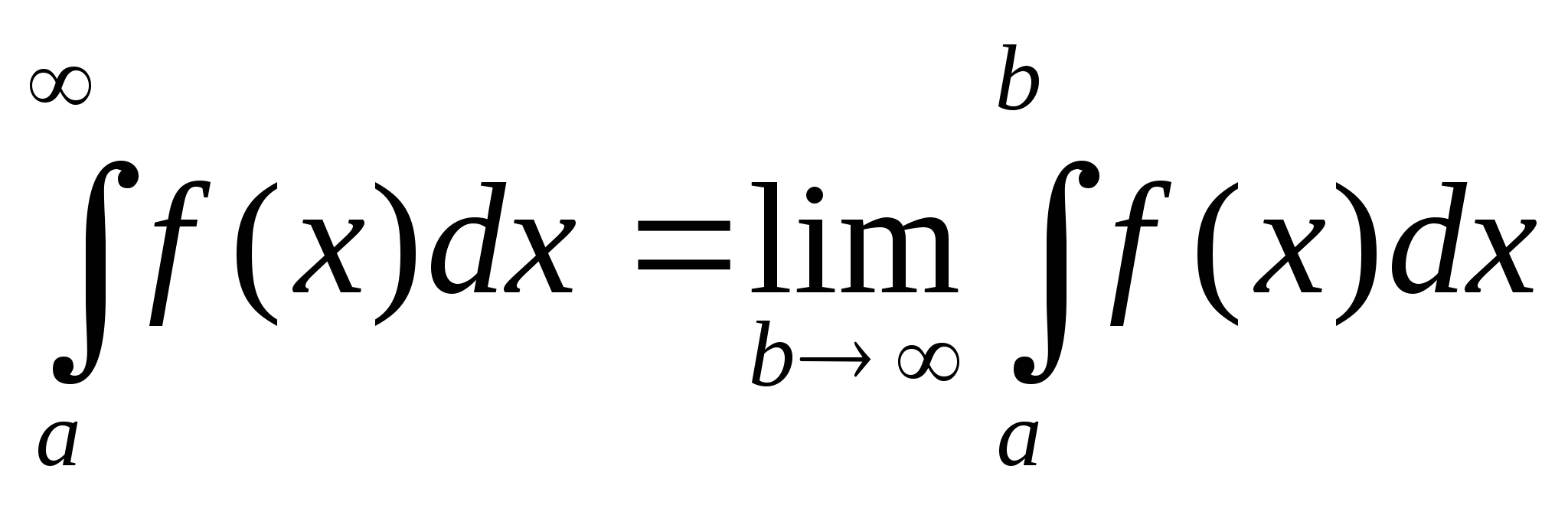
Если данный предел существует, то несобственный интеграл называется сходящимся, а если не существует или равен бесконечности, то расходящимся.
Аналогично определяются несобственные интегралы и для других бесконечных интервалов.
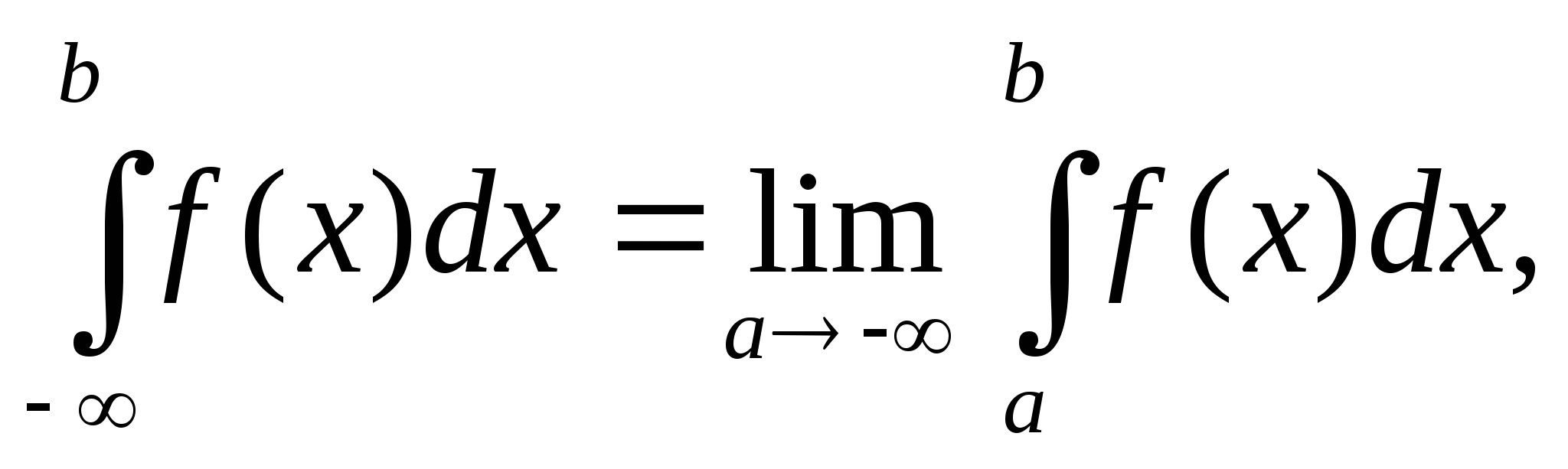
f(x) непрерывна ![]() .
.
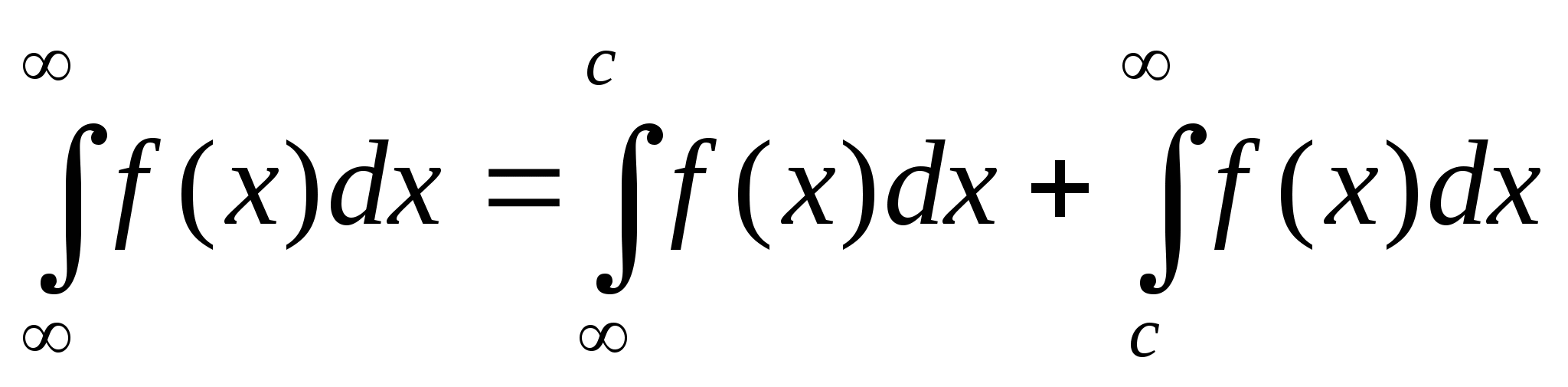 (*)
(*)
f(x) непрерывна ![]() , с - любая точка оси Ох.
, с - любая точка оси Ох.
Замечание. В равенстве (*) интеграл, стоящий слева, сходится только тогда, когда сходятся (существуют) оба интеграла в правой части равенства.
Геометрический смысл сходящегося несобственного интеграла
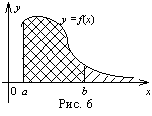
Если ![]() , то
, то 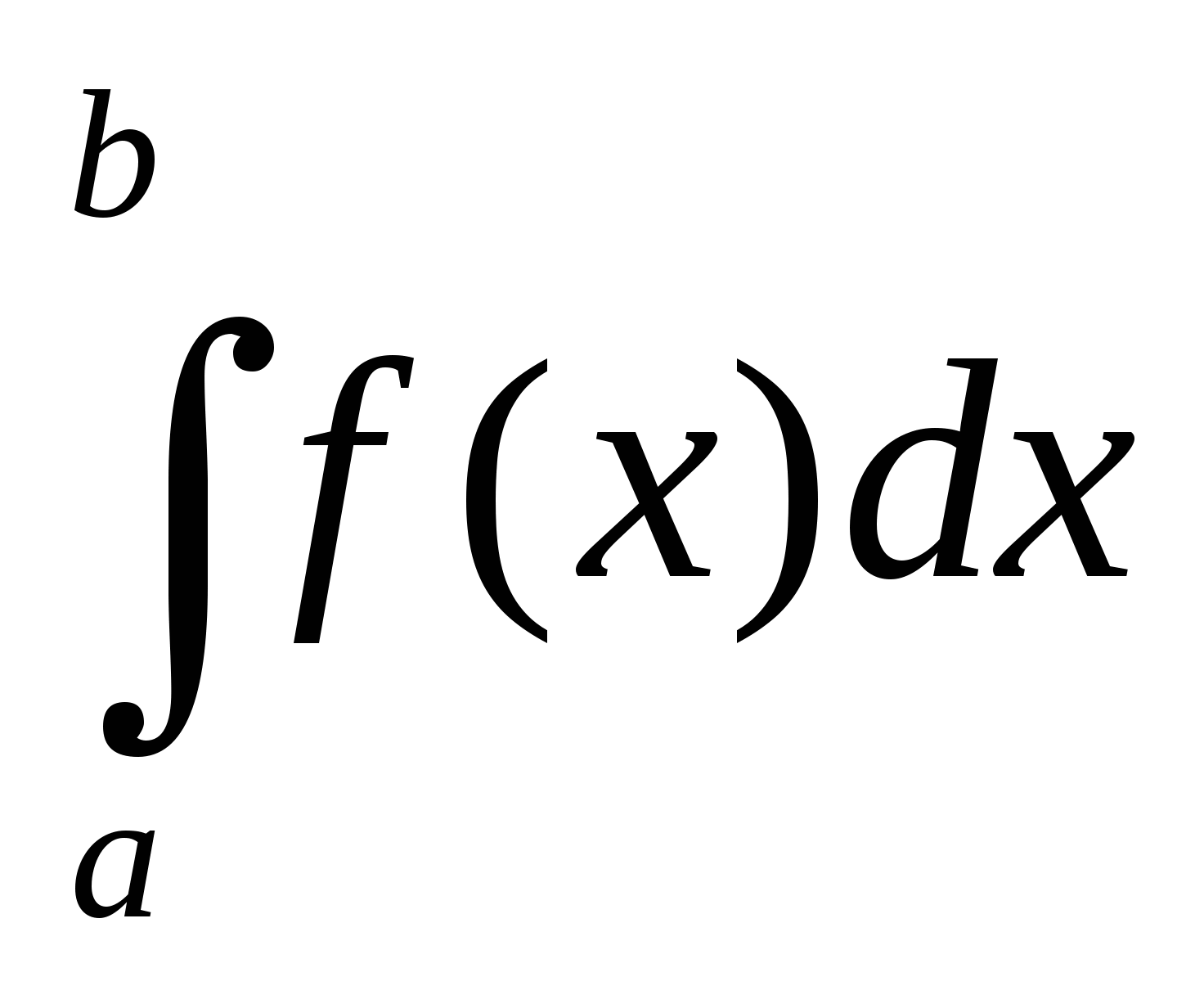 выражает площадь области, ограниченной кривой y=f(x) и прямыми y=0
(ось Ох), x=a, x=b. Поэтому естественно считать, что
выражает площадь области, ограниченной кривой y=f(x) и прямыми y=0
(ось Ох), x=a, x=b. Поэтому естественно считать, что 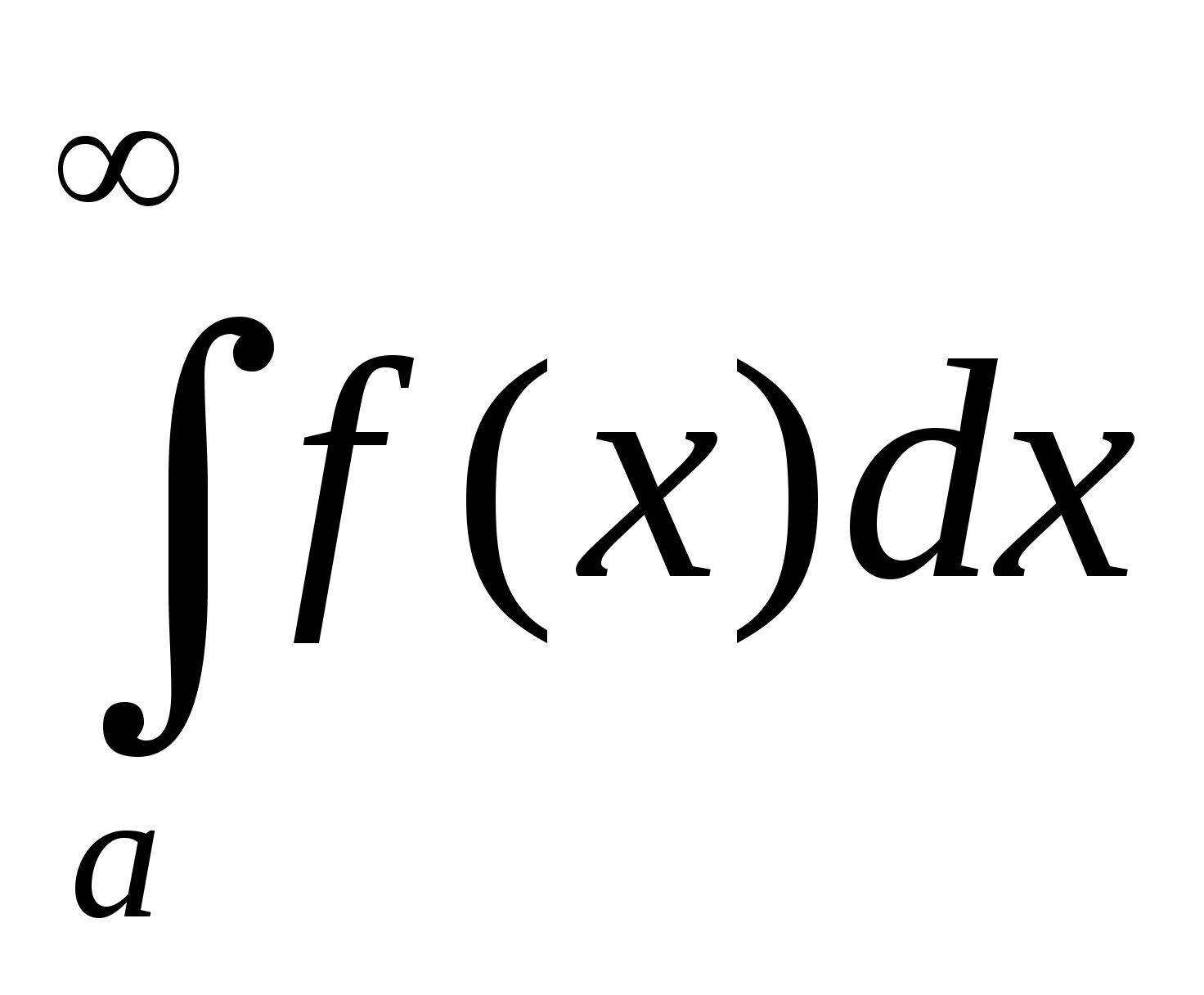 выражает площадь трапеции с бесконечно большим основанием,
заключённой между линиями y=0, x=a и y=f(x).
выражает площадь трапеции с бесконечно большим основанием,
заключённой между линиями y=0, x=a и y=f(x).
Расходящийся несобственный интеграл не имеет какого-либо геометрического смысла.
Иногда бывает достаточно установить, сходится данный интеграл или расходится, и оценить его значение, не вычисляя самого значения. Для этого можно воспользоваться теоремой:
Теорема.
Пусть для всех x (![]() )
выполняется неравенство
)
выполняется неравенство ![]() .
.
Тогда
1. если 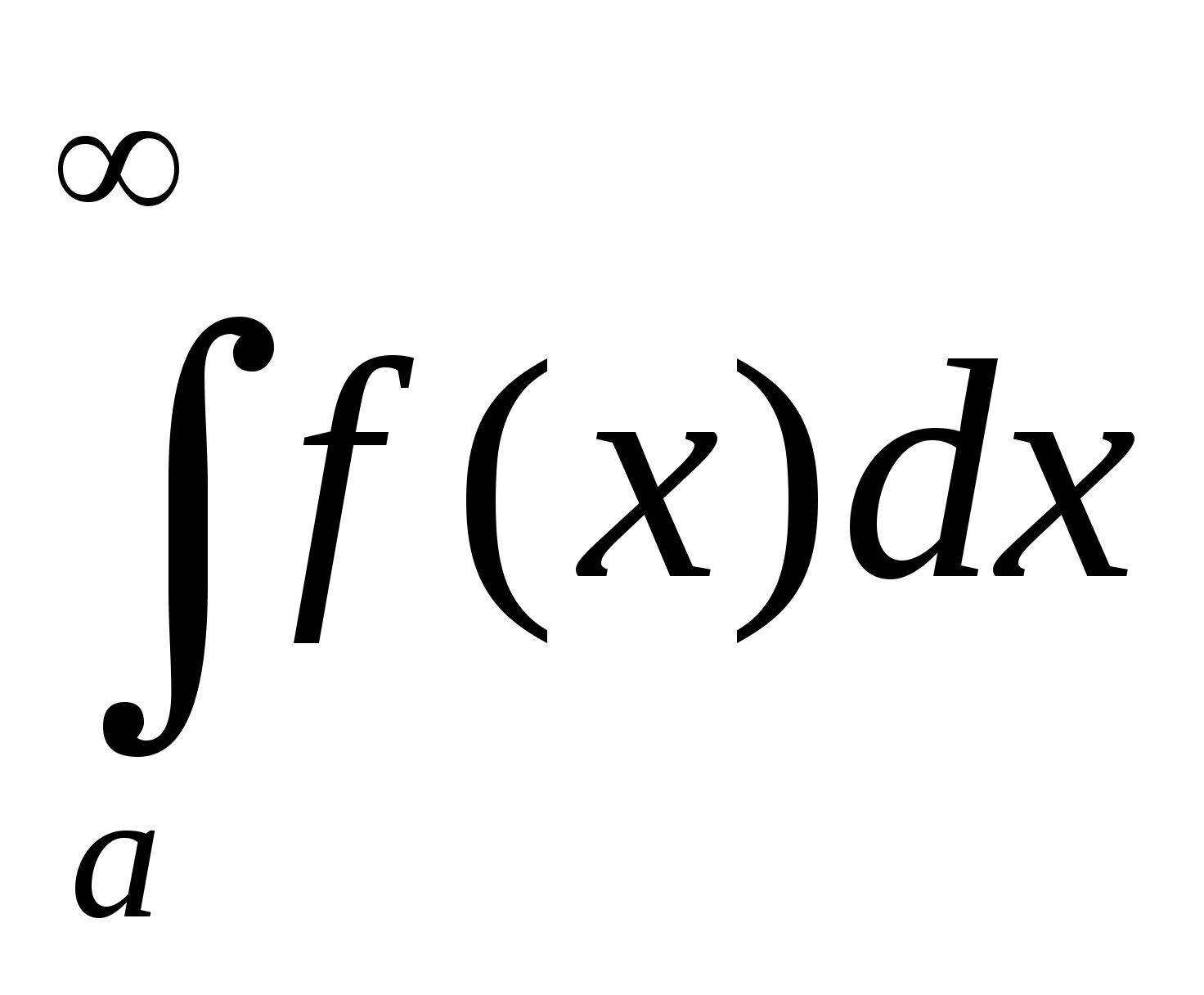 расходится, то расходится и
расходится, то расходится и 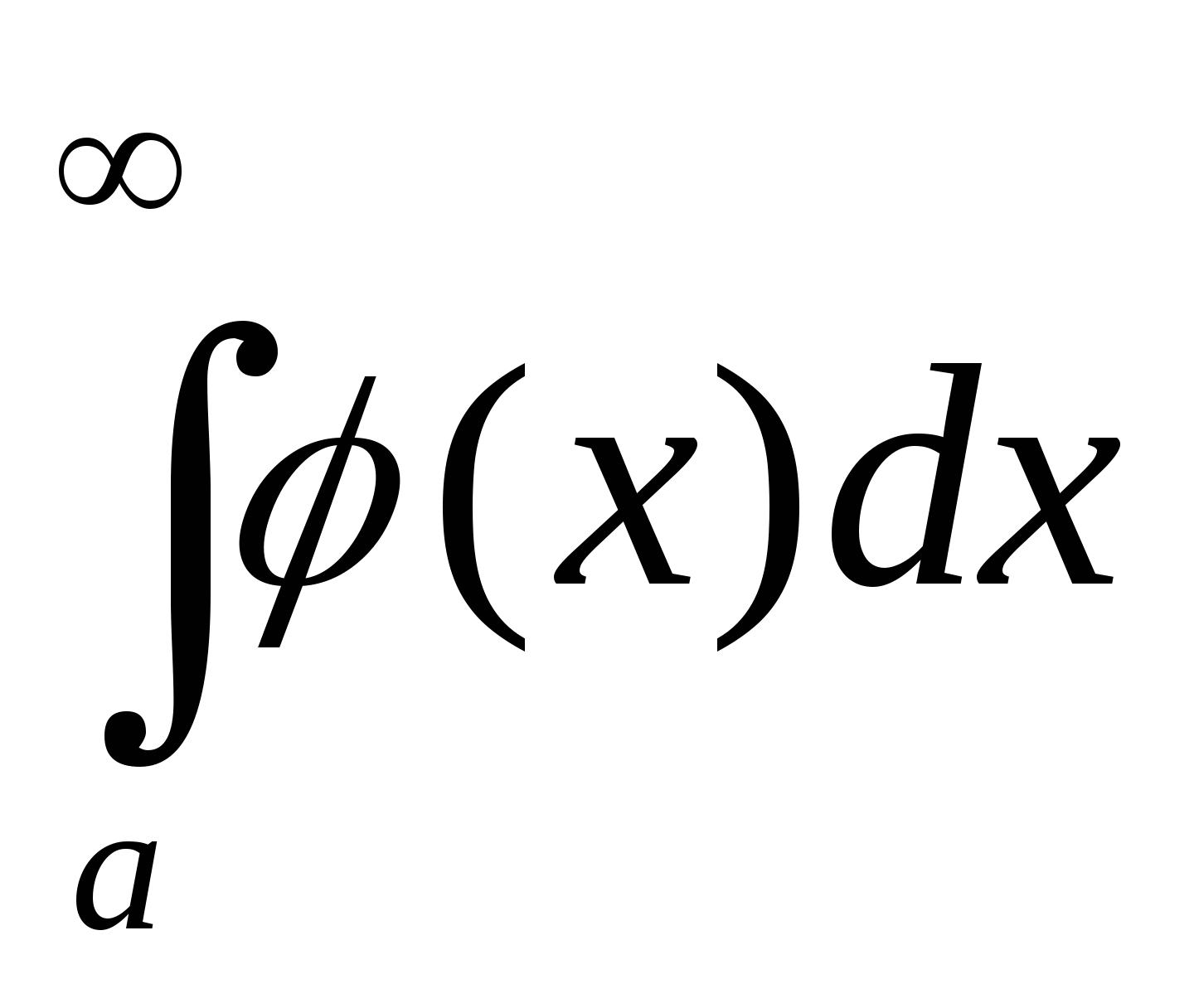 ;
;
2. если 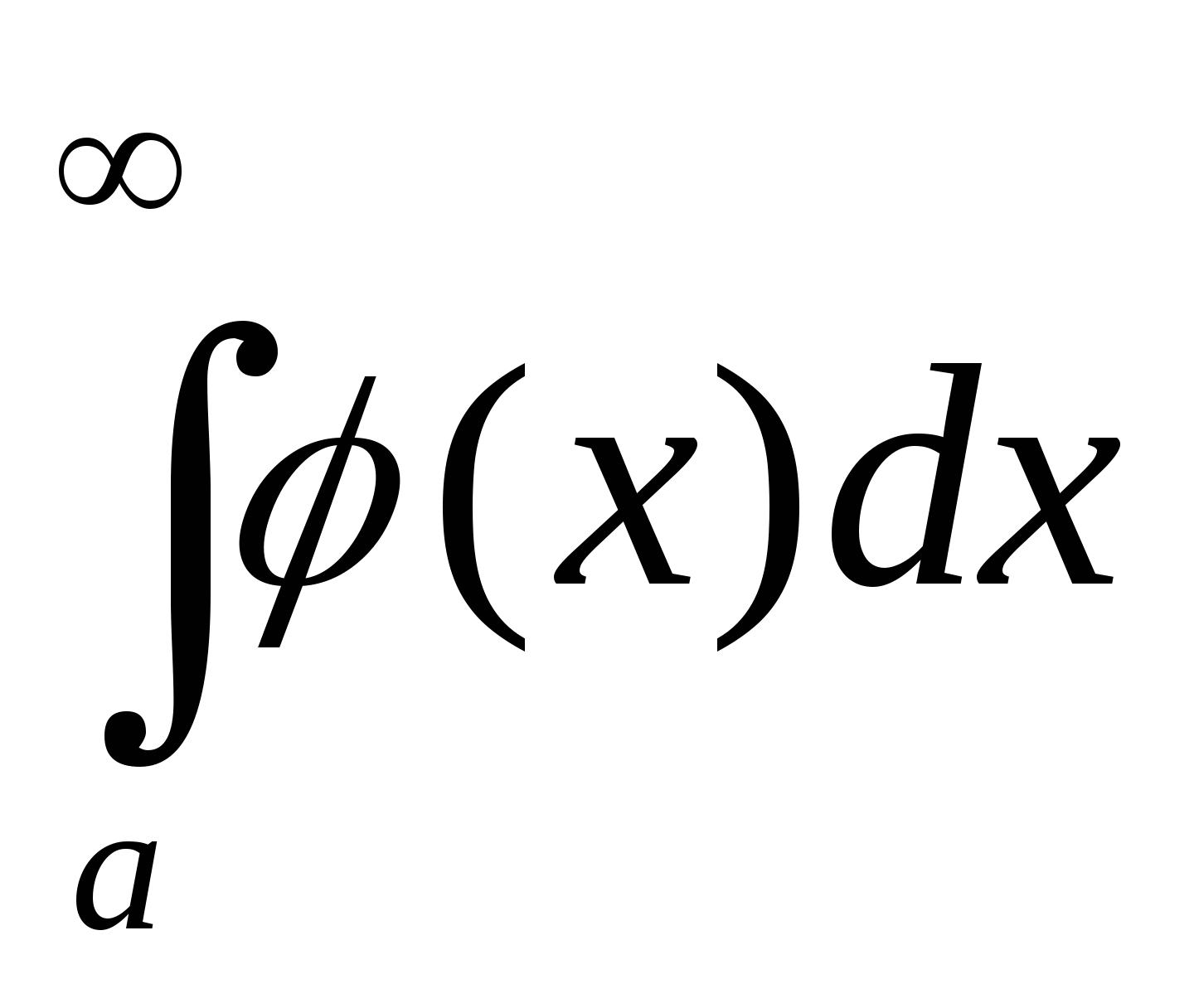 сходится, то сходится и
сходится, то сходится и 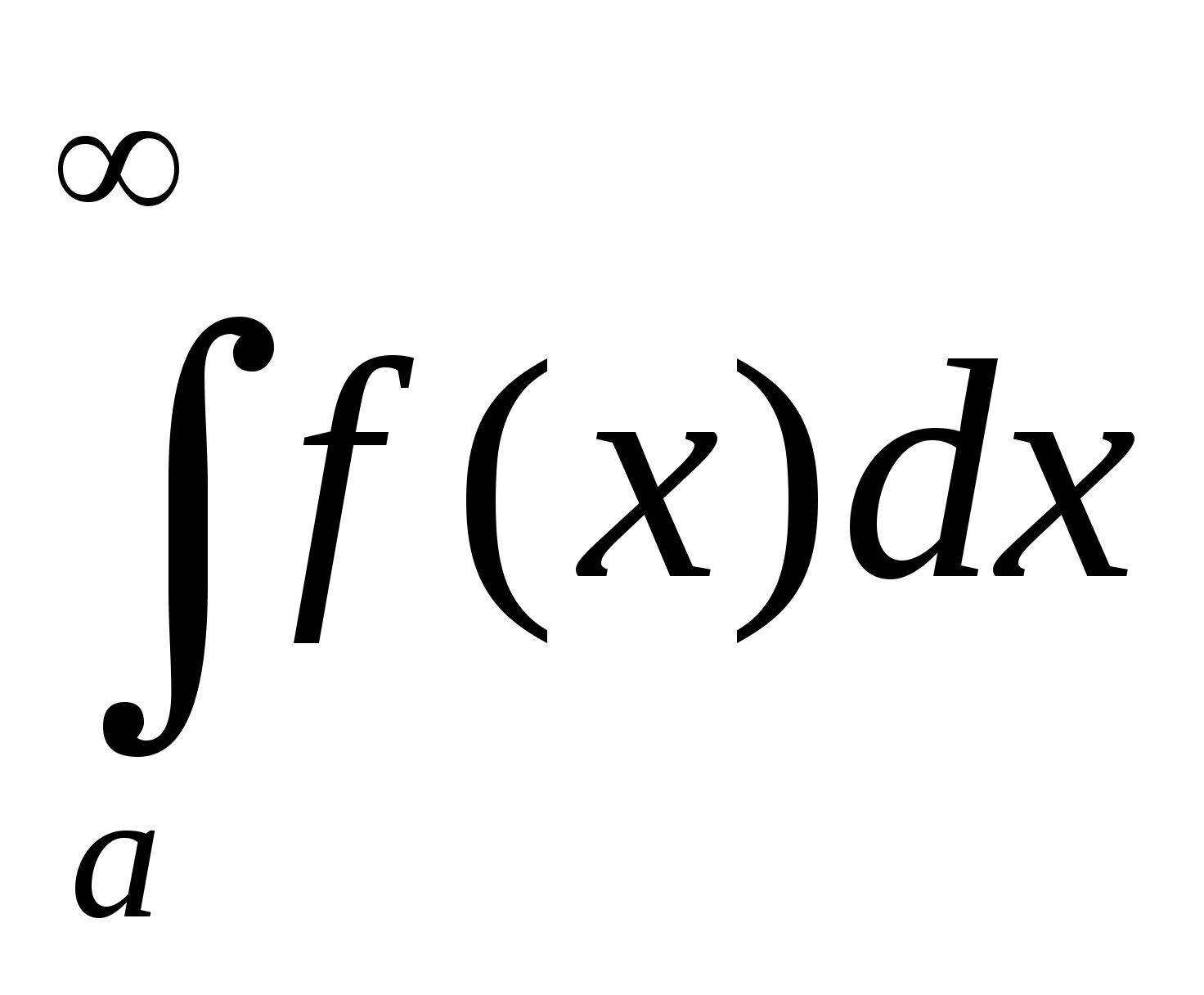 , при этом
, при этом 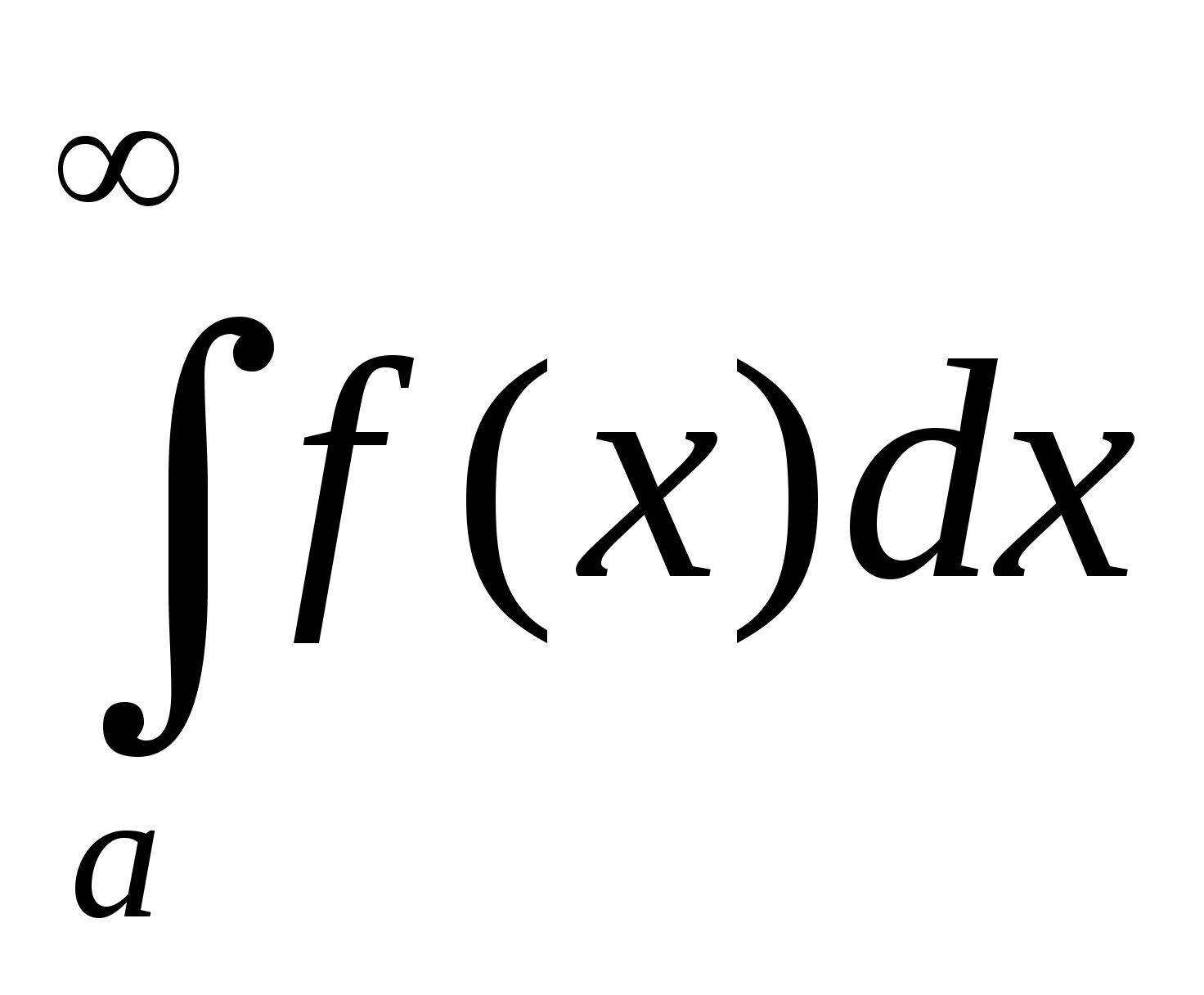
![]()
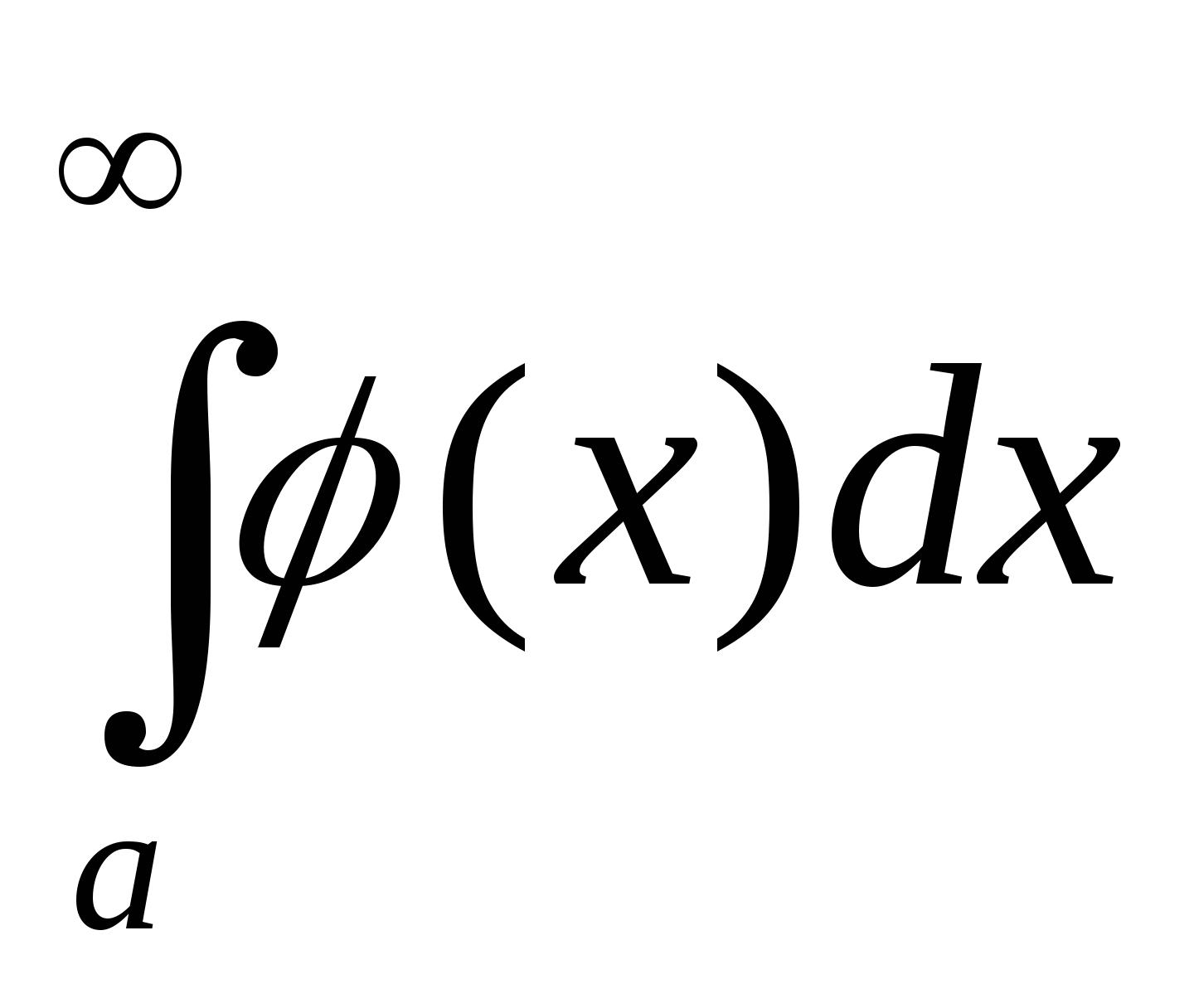 ;
;
3. если ![]() то интегралы
то интегралы 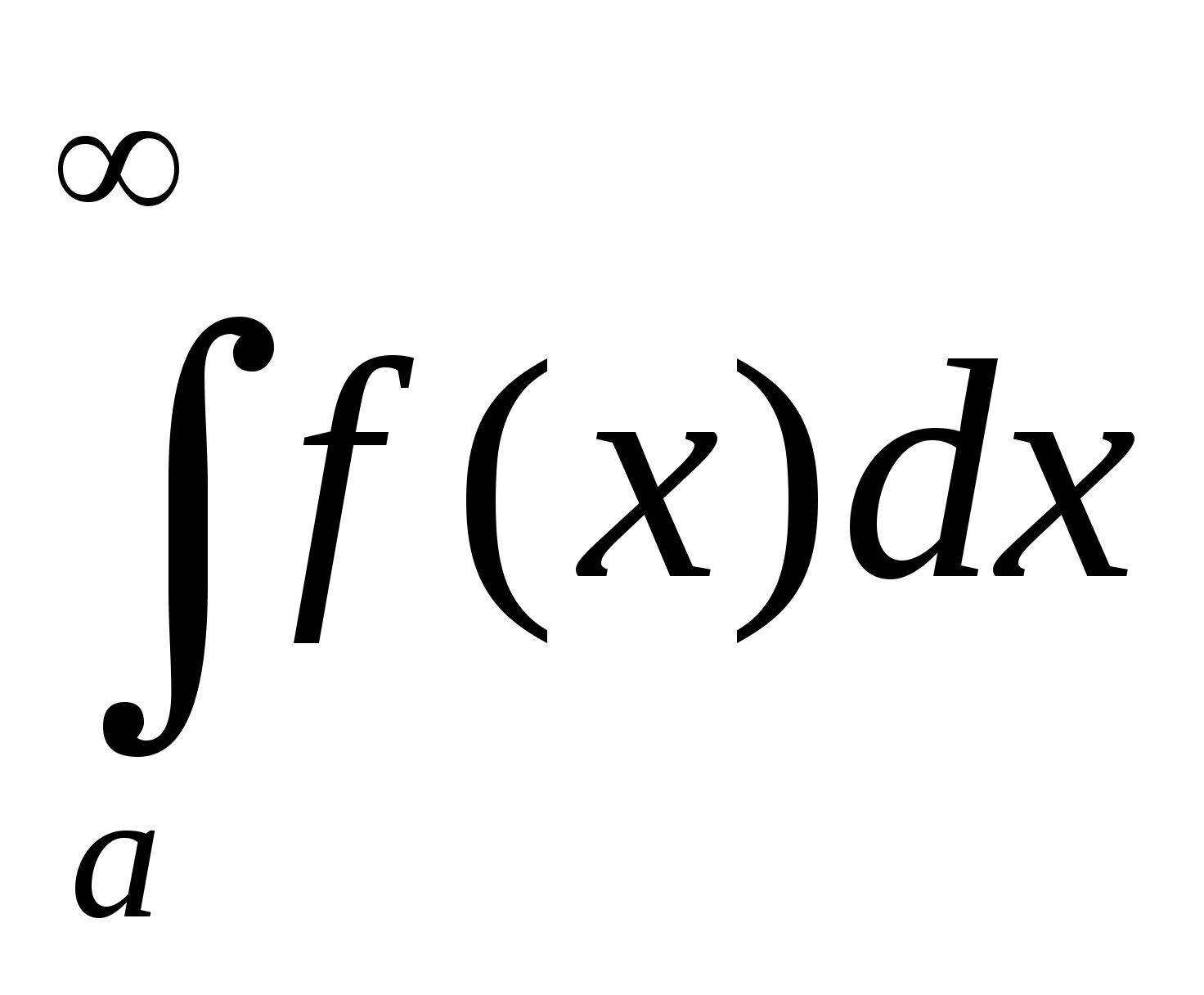 и
и 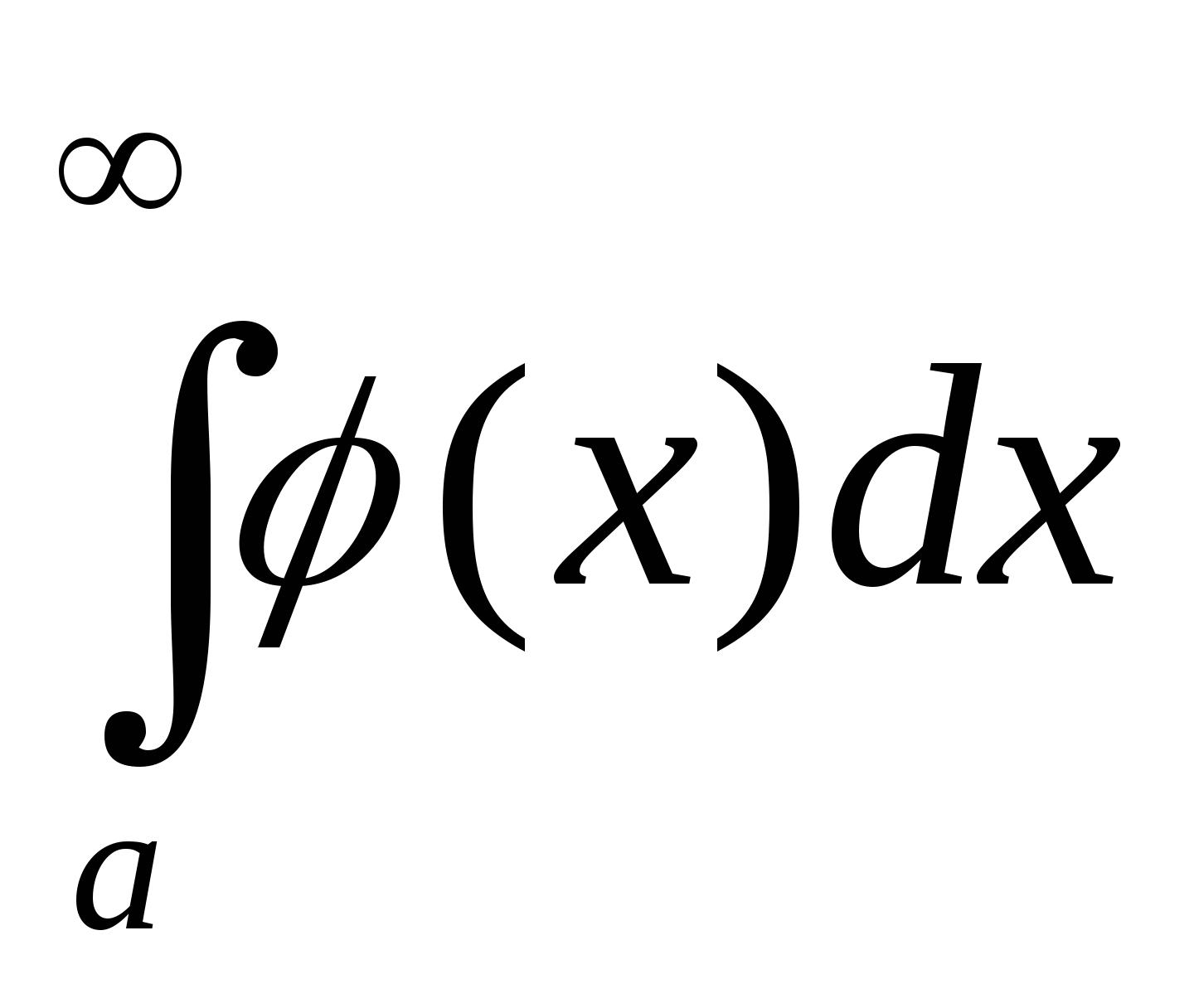
(Либо оба сходятся, либо оба расходятся.)
Несобственные интегралы с бесконечными пределами называют несобственными интегралами I рода.
Интегралы от разрывных функций
Пусть функция y=f(x) для всех значений ![]() , но при x=b претерпевает бесконечный разрыв. Обычное определение
интеграла в этом случае теряет смысл.
, но при x=b претерпевает бесконечный разрыв. Обычное определение
интеграла в этом случае теряет смысл.
Определение. Несобственным интегралом от функции
f(x), непрерывной при ![]() и неограниченной при
и неограниченной при ![]() , называется предел интеграла
, называется предел интеграла 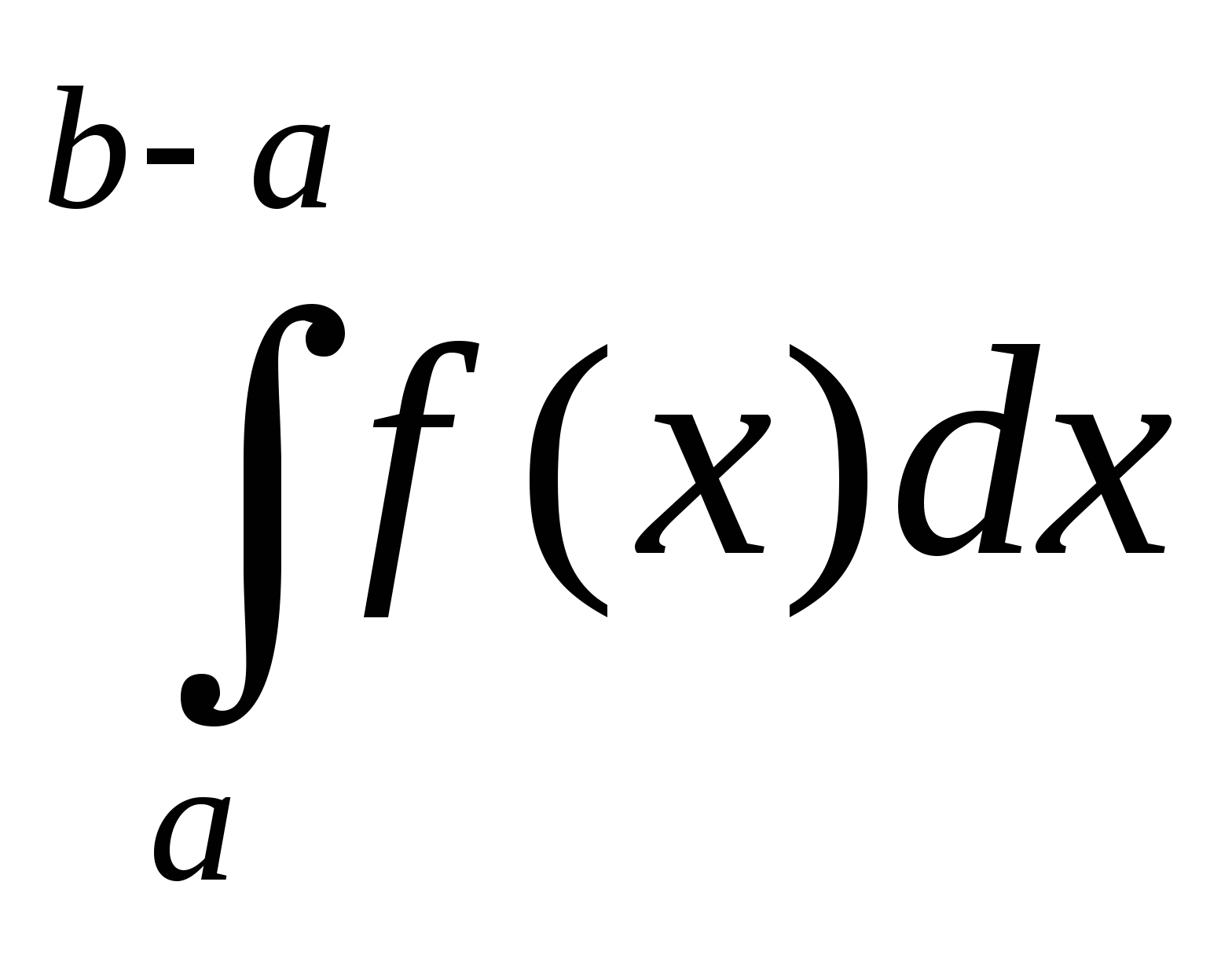 при
при ![]()
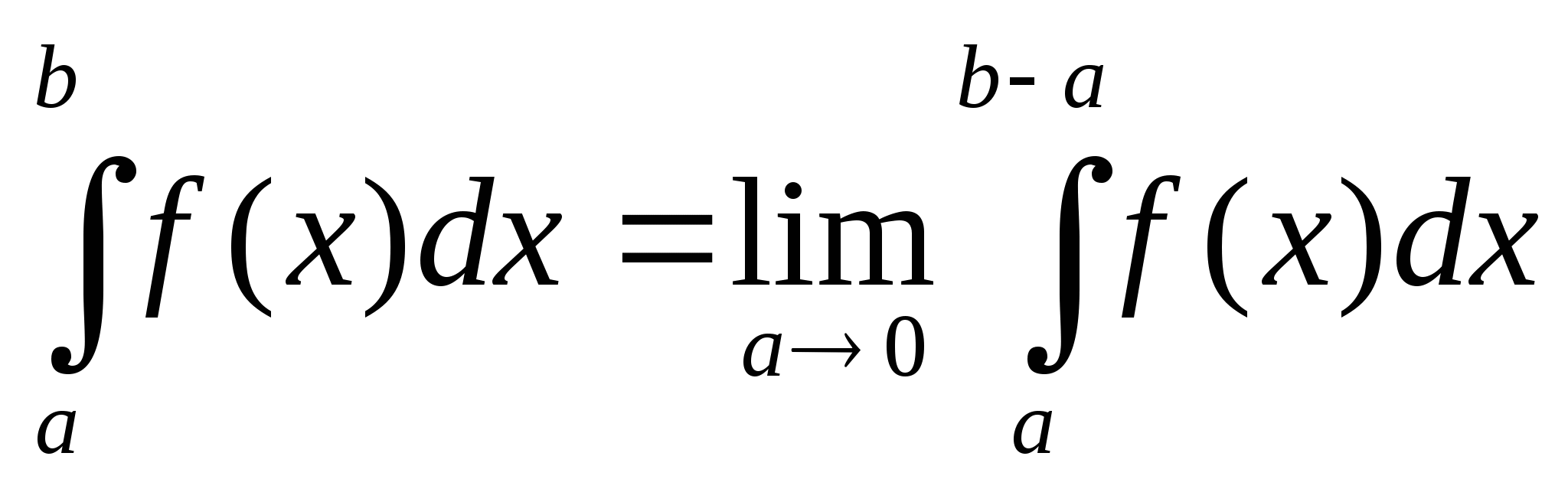
Если данный предел существует, то несобственный интеграл называется сходящимся, а если не существует или бесконечен, то расходящимся.
Аналогично если функция f(x) претерпевает бесконечный разрыв при x=a, то
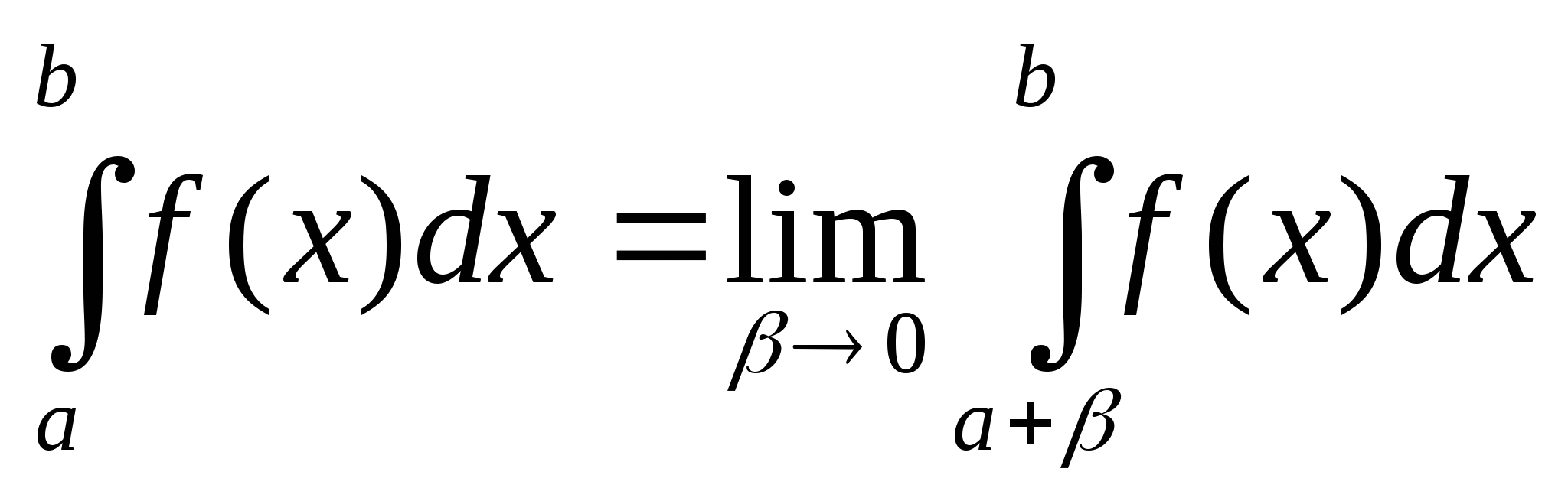
Если же функция имеет бесконечный разрыв в какой-нибудь точке с (a<c<b), то
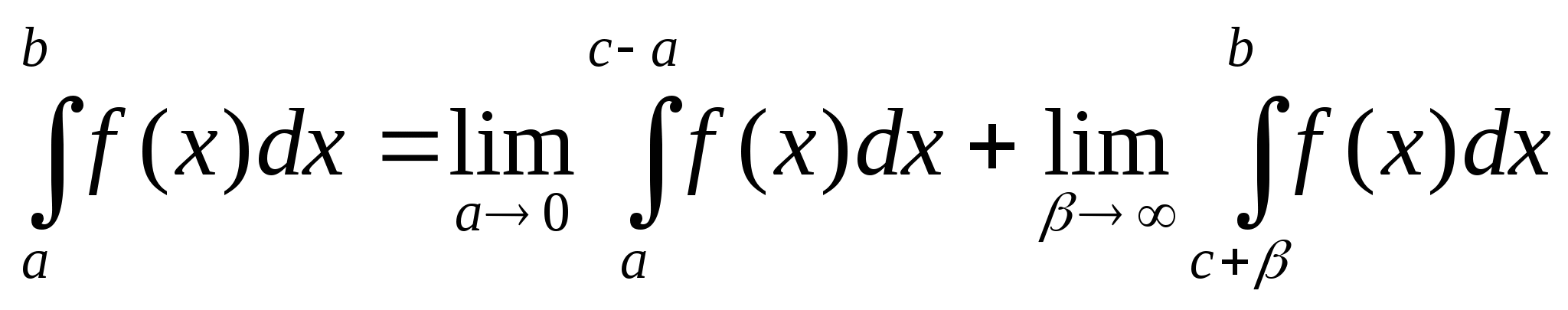 ,
причём a и b стремится к нулю независимо друг от друга.
,
причём a и b стремится к нулю независимо друг от друга.
Для определения сходимости несобственных интегралов от разрывных функций полезно воспользоваться следующей теоремой.
Теорема.
Если на отрезке ![]() функции f(x) и
функции f(x) и ![]() имеют единственную особенность в точке b, причём во всех точках
этого отрезка выполняются неравенства
имеют единственную особенность в точке b, причём во всех точках
этого отрезка выполняются неравенства ![]() то
то
1. если 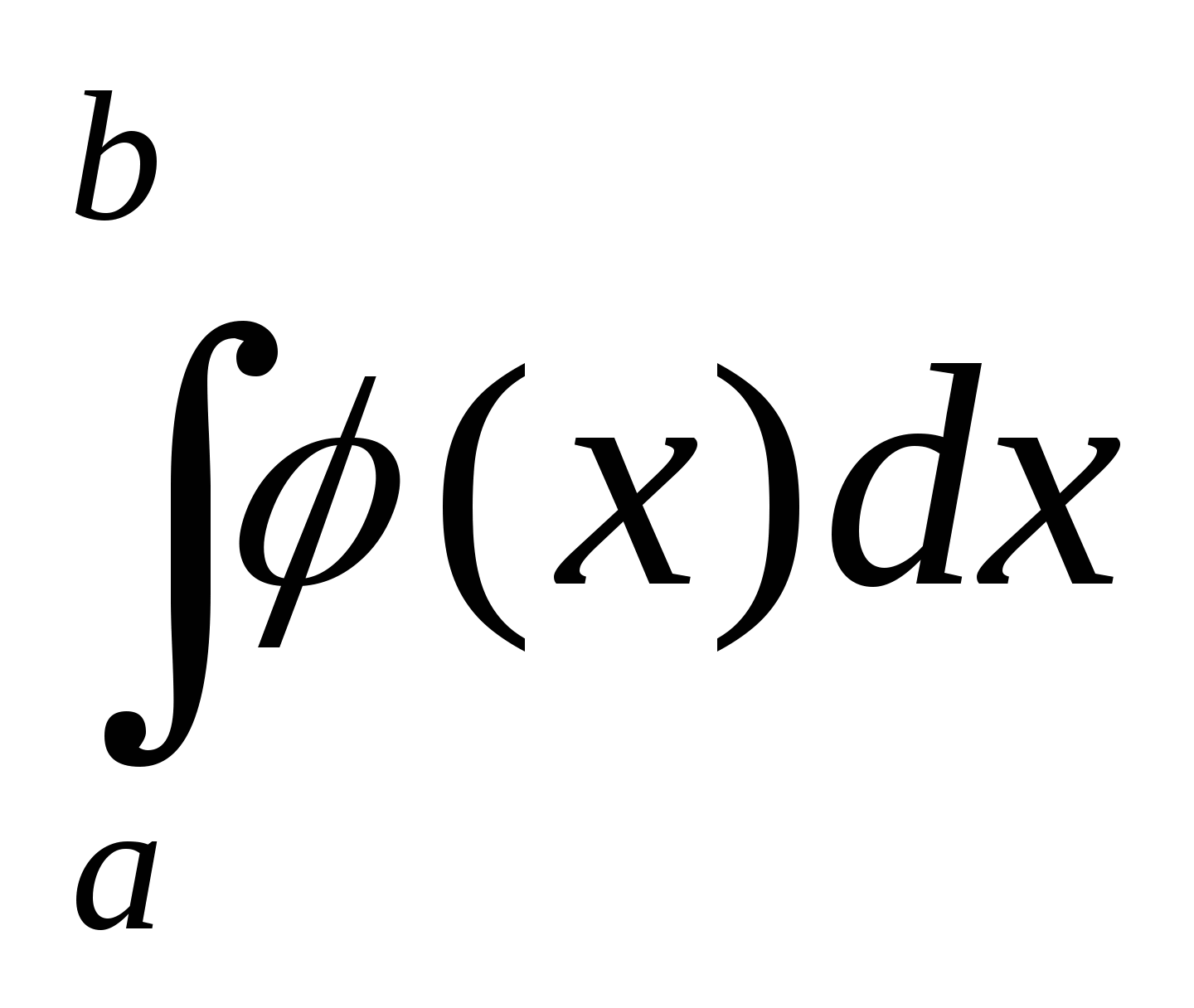 сходится, то сходится и
сходится, то сходится и 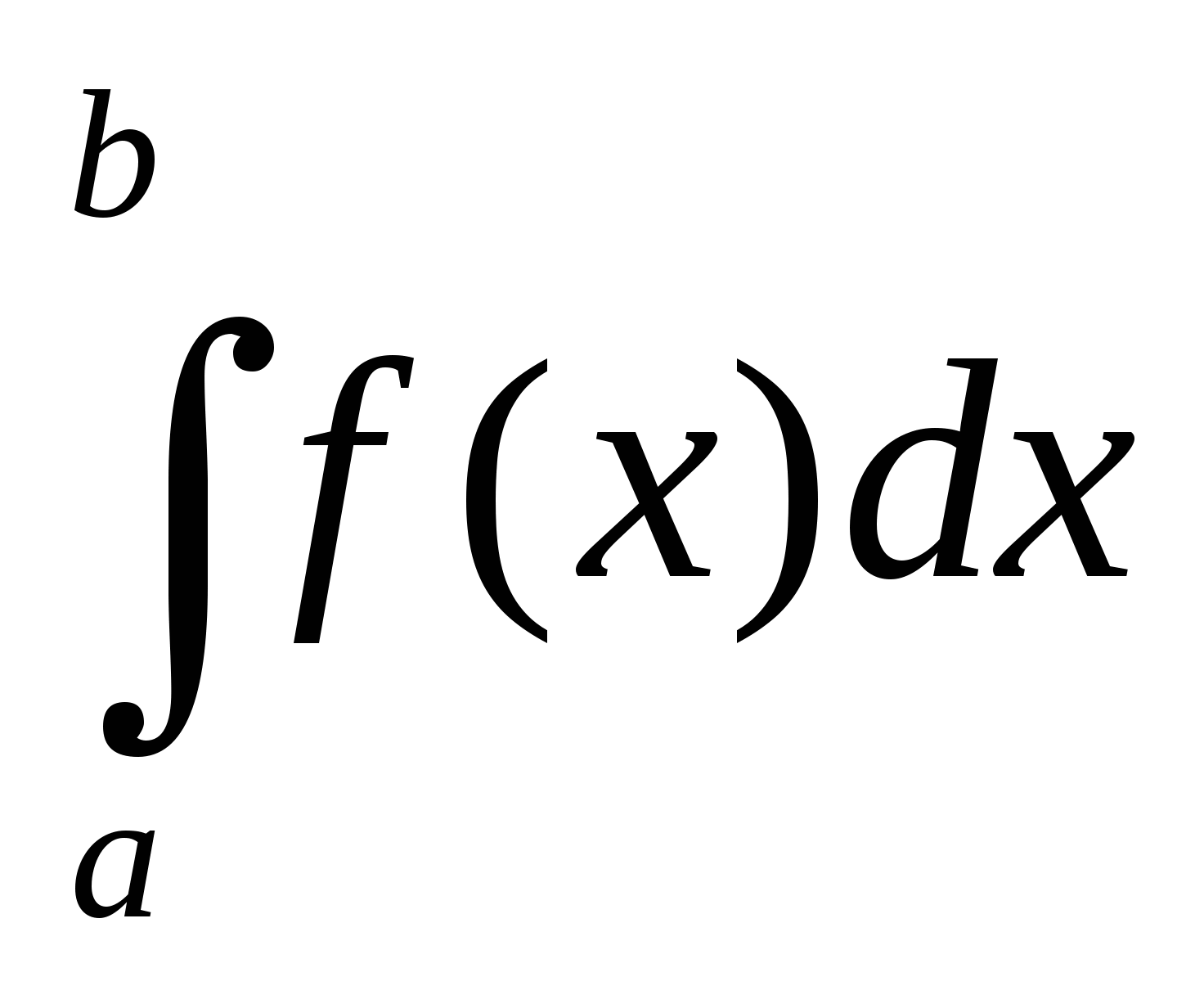 ;
;
2. если 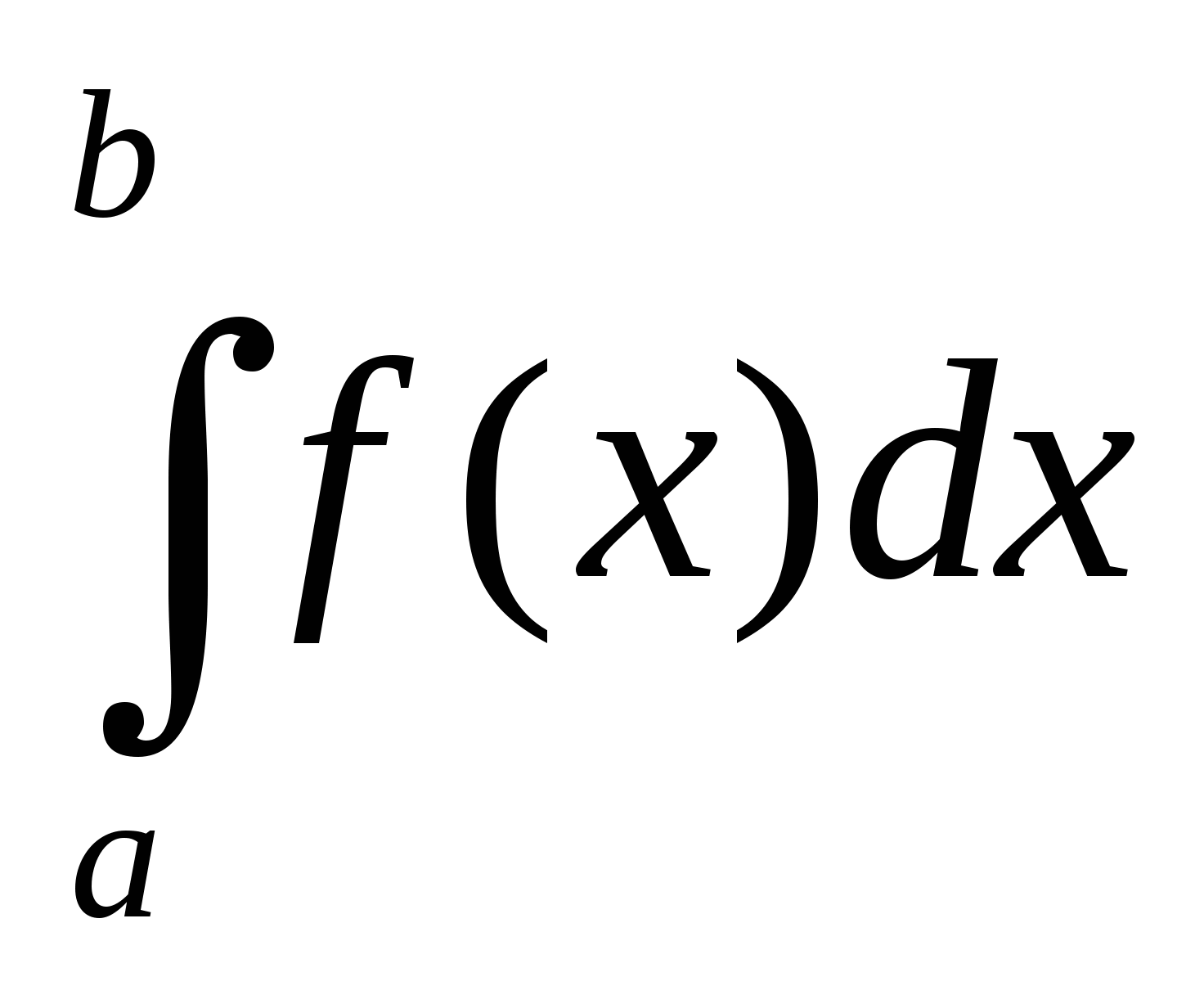 расходится, то
расходится, то 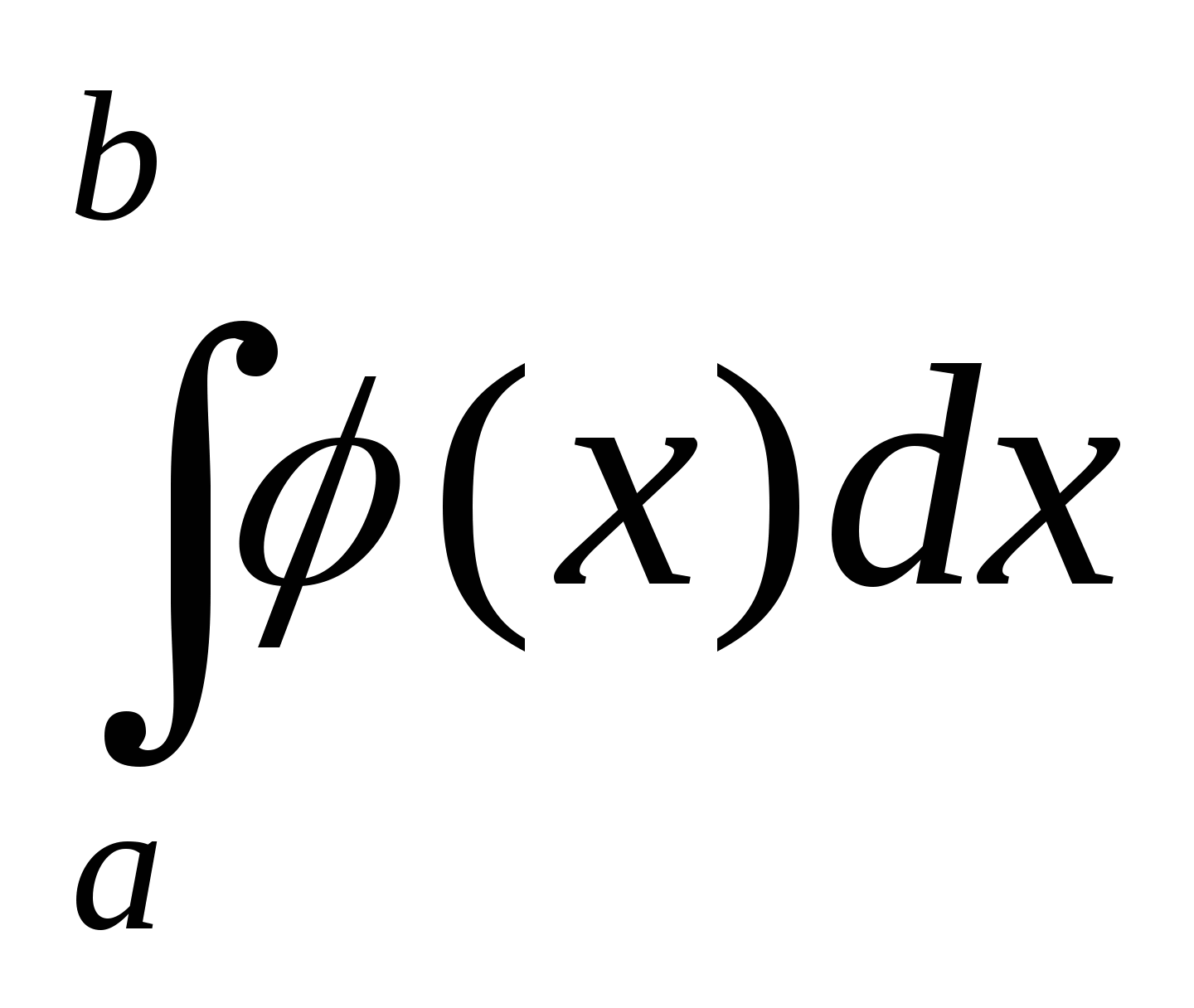 тоже расходится.
тоже расходится.
Несобственные интегралы от разрывных функций называются несобственными интегралами II рода.
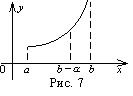
Геометрическая интерпретация сходящегося несобственного интеграла II рода - это площадь криволинейной трапеции с бесконечно большой высотой.
Заключение
В работе рассмотрены вопросы теории интегрального исчисления функции одной переменной, такие как первообразная и её свойства, неопределённый интеграл и его свойства, замена переменной в определённом интеграле, интегрирование по частям, циклический интеграл, интегрирование рациональных дробей, интегрирование тригонометрических функций, интегрирование иррациональностей, приближённое вычисление определённого интеграла, определённый интеграл и его свойства, вычисление площадей плоской области, длина дуги кривой, несобственные интегралы. Составлены и решены тестовые задания по этим темам, причём задания 1-5, 9-17, 27, 29, 43, 58-59 - метод замены переменной и основные свойства неопределённого интеграла; задания 6-8, 18, 23-24 - метод интегрирования по частям; задания 25-26, 28, 41-42, 44 - интегрирование рациональных дробей; задания 30, 46-57 - интегрирование тригонометрических функций; задание 60 - использование стандартной формулы дифференциального бинома; задания 61-66, 86-88 - вычисление определённого интеграла; задания 79-81 - вычисление площади с помощью определённого интеграла; задания 82-84 - вычисление длины дуги; задание 85 - вычисление объёма шара; задания 31-40 - теоретические вопросы по темам: первообразная и её свойства, неопределённый интеграл, его свойства, основные правила интегрирования, замена переменной в неопределённом интеграле, интегрирование по частям, циклический интеграл; задания 67-78 - теоретические вопросы по темам: приближённые методы, определённый интеграл, задачи, приводящие к понятию определённого интеграла: о площади трапеции, свойства определённого интеграла, задания 89-100 - теоретические вопросы по темам: вычисление площадей с помощью определённого интеграла в декартовой системе координат, вычисление длины дуги, вычисление объёма методом параллельных сечений, объём тела вращения, несобственные интегралы.
Предполагается, что все задания имеют базовый уровень сложности.
Тесты
Первообразная и её свойства. Неопределённый интеграл, его свойства. Основные правила интегрирования.
Замена переменной в неопределённом интеграле, интегрирование по частям. Циклический интеграл.
1. ![]()
a)![]() b)
b) ![]()
c) ![]() d)
d) ![]()
Решение задачи 1.
Интегрируем, используя свойства:
![]()
![]()
2. ![]()
a) ![]() b)
b) ![]()
c) ![]() d)
d) ![]()
Решение задачи 2.
Интегрируем методом замены: 6![]()
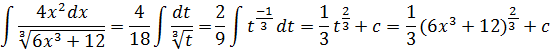
3. ![]()
a) ![]() b)
b) ![]()
c) ![]() d)
d) ![]()
Решение задачи 3.
Используем подстановку: ![]() ,
, ![]()
![]()
4. ![]()
a)![]() b)
b)![]() c)
c) ![]() d)
d)![]()
Решение задачи 4.
![]() =
=![]()
5.![]()
a) ![]() b)
b) ![]() c)
c)![]() d)
d)![]()
Решение задачи 5.
![]()
![]()
![]()
6.![]()
a)- ![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 6.
Пусть u=x, dv=![]() dx
=> du=dx,
dx
=> du=dx, ![]()
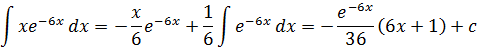
7.![]()
a) ![]() b)
b)![]()
c)![]() d)
d)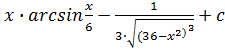
Решение задачи 7.
u=arcsin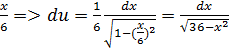 , dv=dx
, dv=dx![]() v=x
v=x
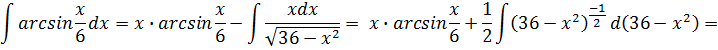
= ![]()
8.![]()
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 8.
Пусть u=![]() ,
du=
,
du=![]() ,
dv=(x-6)dx => v=
,
dv=(x-6)dx => v=![]() =>
=>
![]() =
=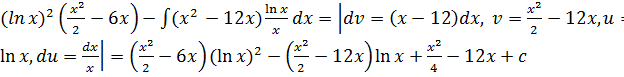
9.![]()
a)![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 9.
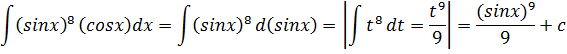
10.![]()
a)![]() b)
b)![]()
c)![]() d)
d)![]()
Решение задачи 10.
В знаменателе присутствует квадратный трёхчлен. Выделяем полный квадрат:
![]()
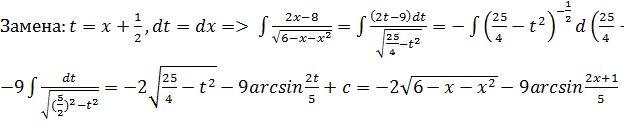
11.![]()
a) ![]() b)
b)![]()
c)![]() d)
d)![]()
Решение задачи 11.
Замена: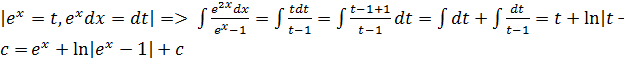
12.Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)sinx+c d)sinx+c
c)sinx+c d)sinx+c
Решение задачи 12.
![]()
13.Чему равен интеграл ![]() ?
?
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 13.
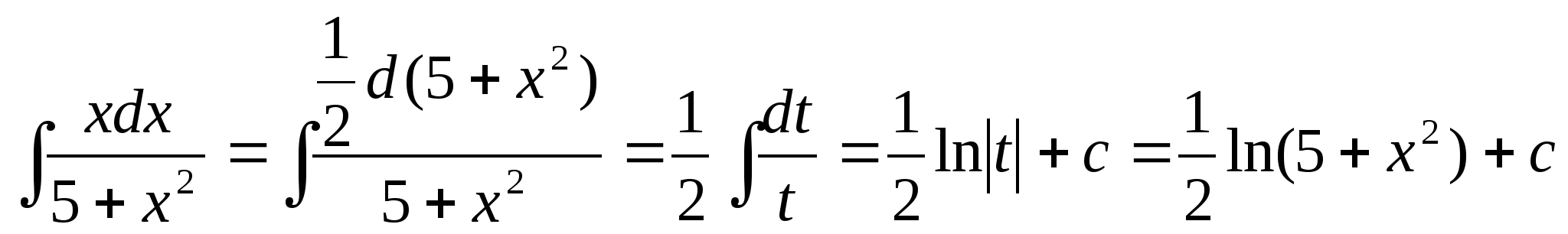
14.Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 14.
![]()
15.Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 15.
![]()
![]()
16.Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 16.
![]() =
=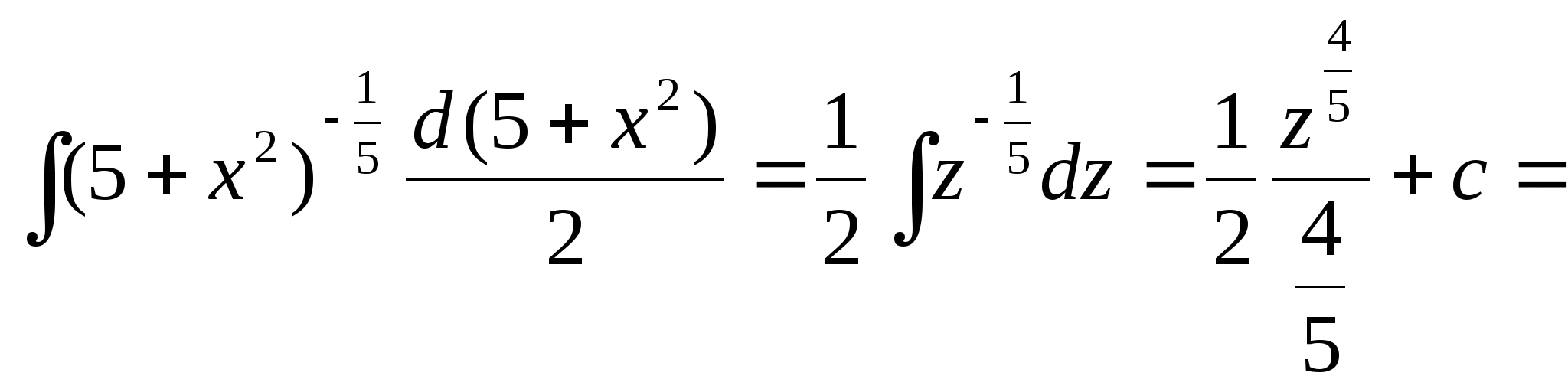
![]()
17.Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 17.
![]()
18.Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 18.
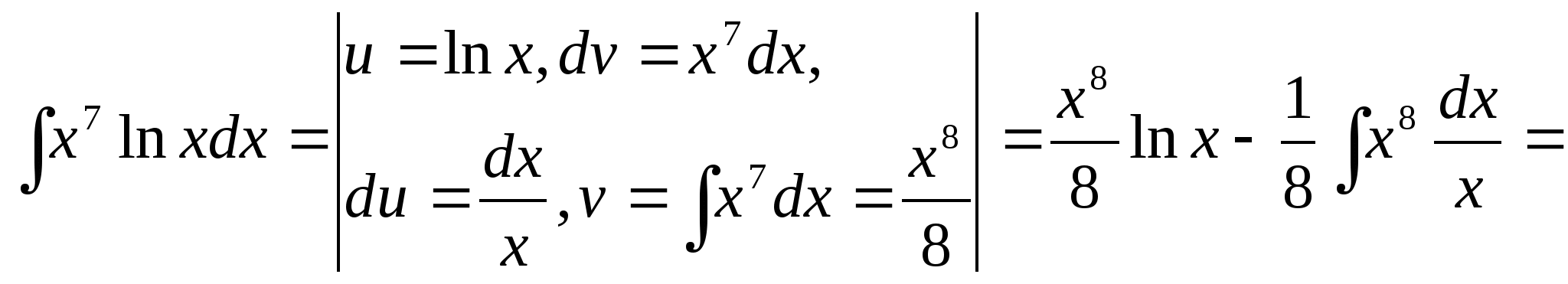
![]()
19. Чему равен интеграл ![]() ?
?
a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 19.
![]()
![]()
20. Чему равен интеграл ![]() ?
?
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 20.
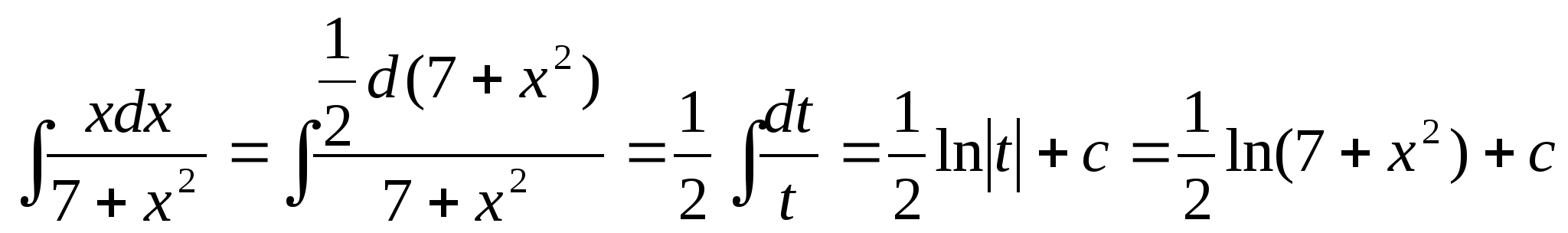
21.Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 21.
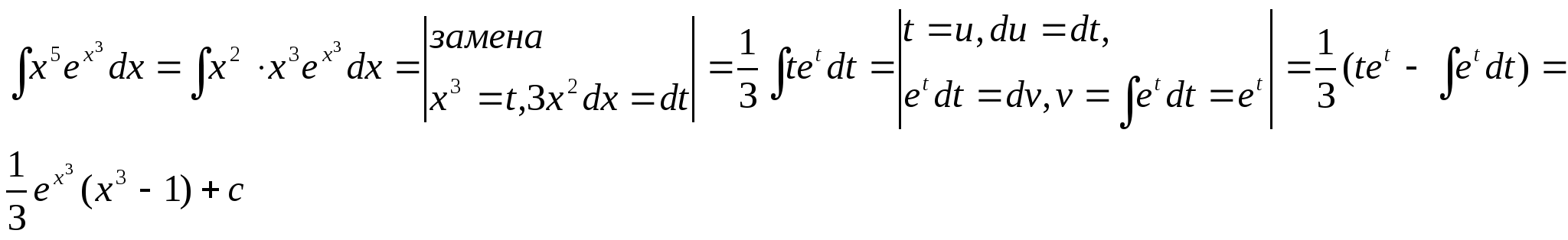
22.Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 22.
Пусть k=1, k+1=2, a=3:
![]()
Последний интеграл табличный: ![]()
![]()
23.Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 23.
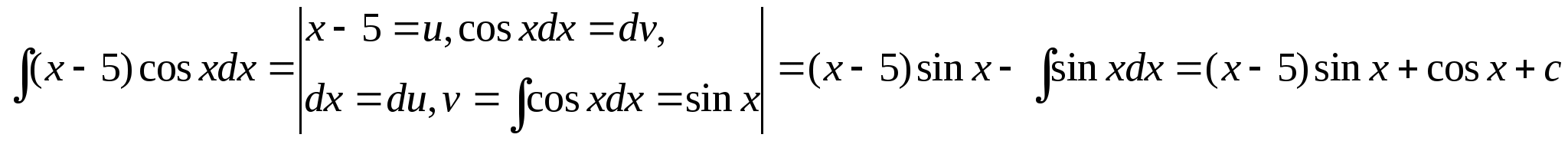
24.Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 24.
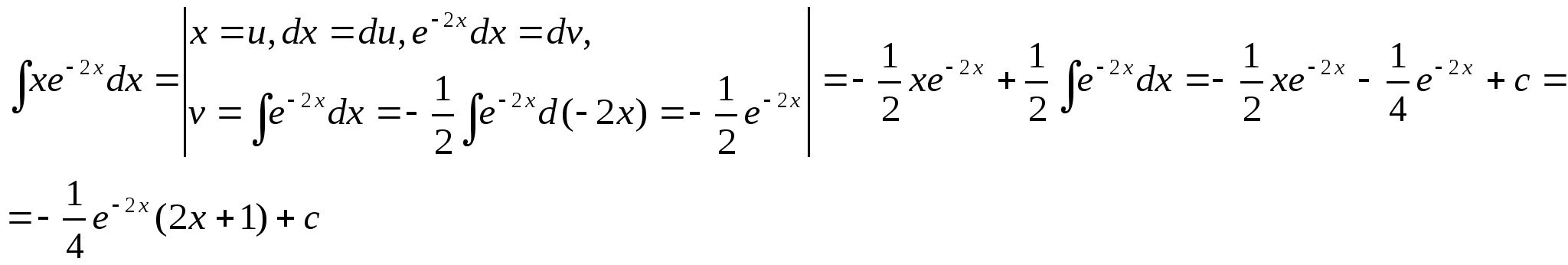
25.Чему равен неопределённый интеграл
![]() ?
?
a)![]()
b) ![]()
c)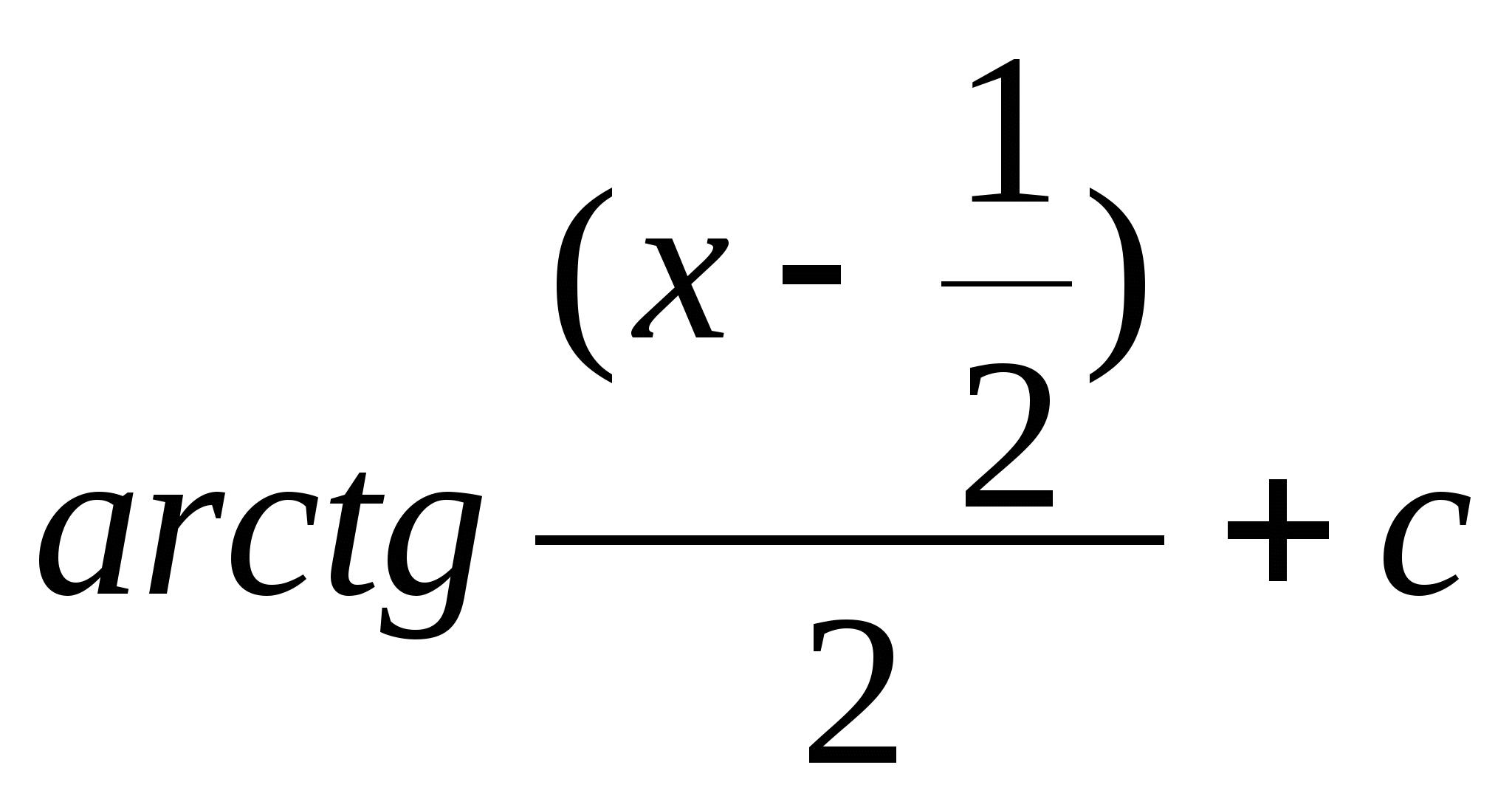
d) 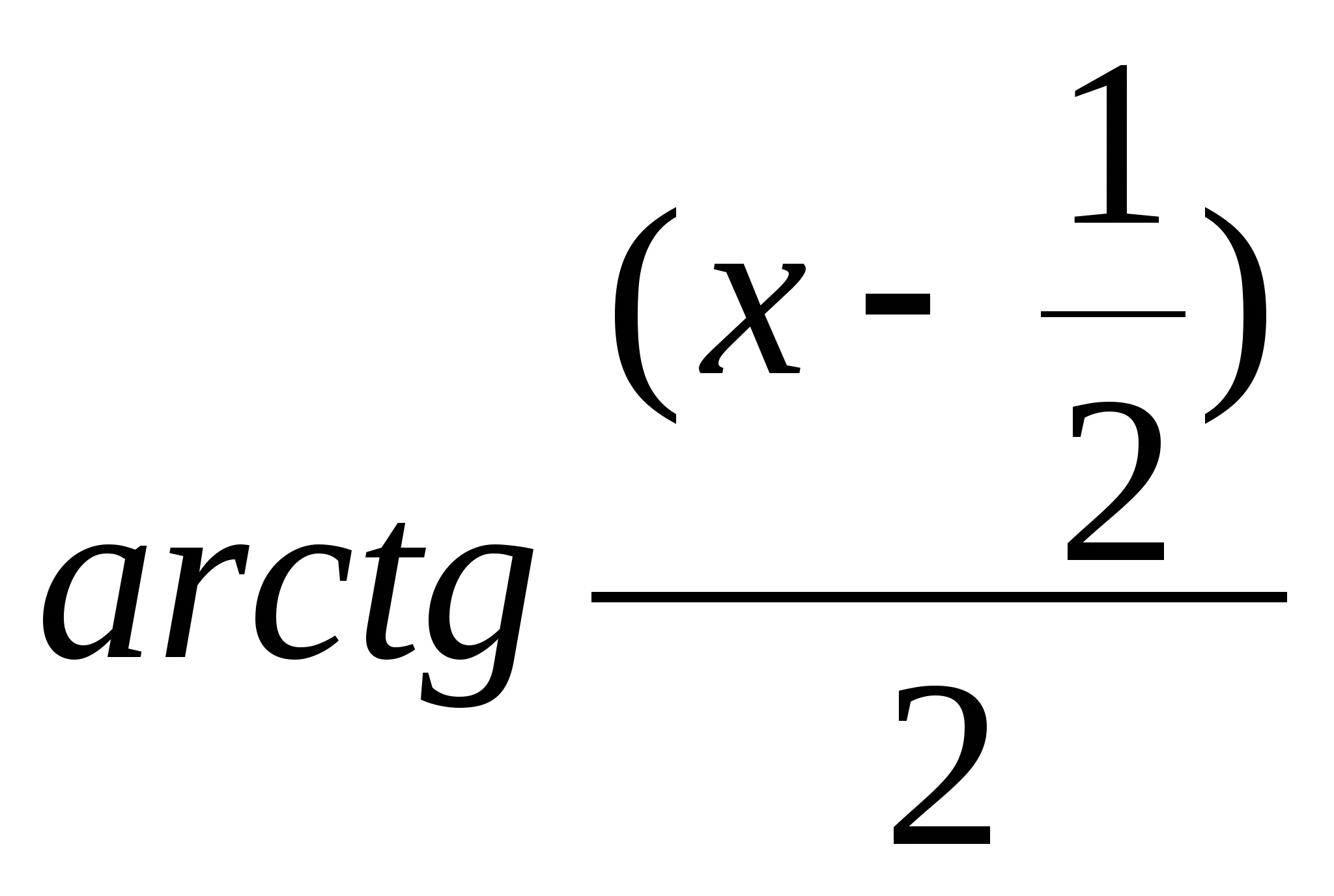
Решение задачи 25.
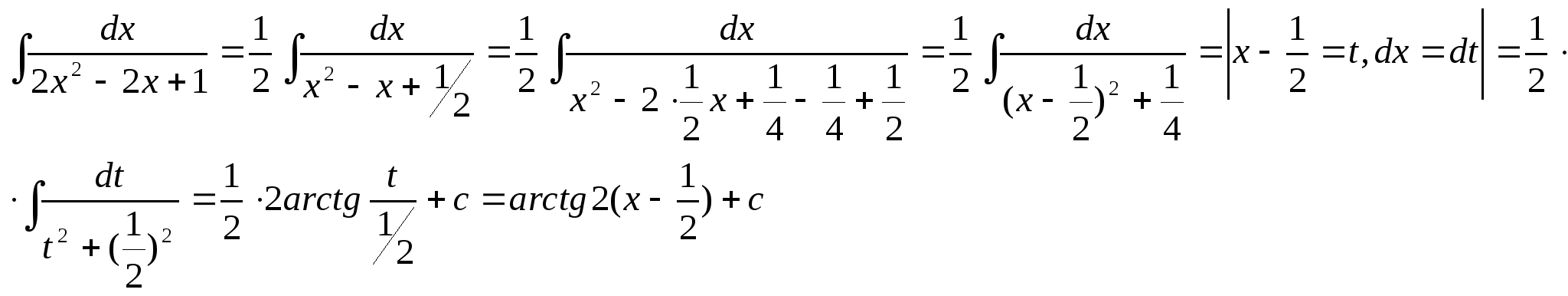
26.Чему равен интеграл ![]()
![]() ?
?
a)![]()
b) ![]()
c) 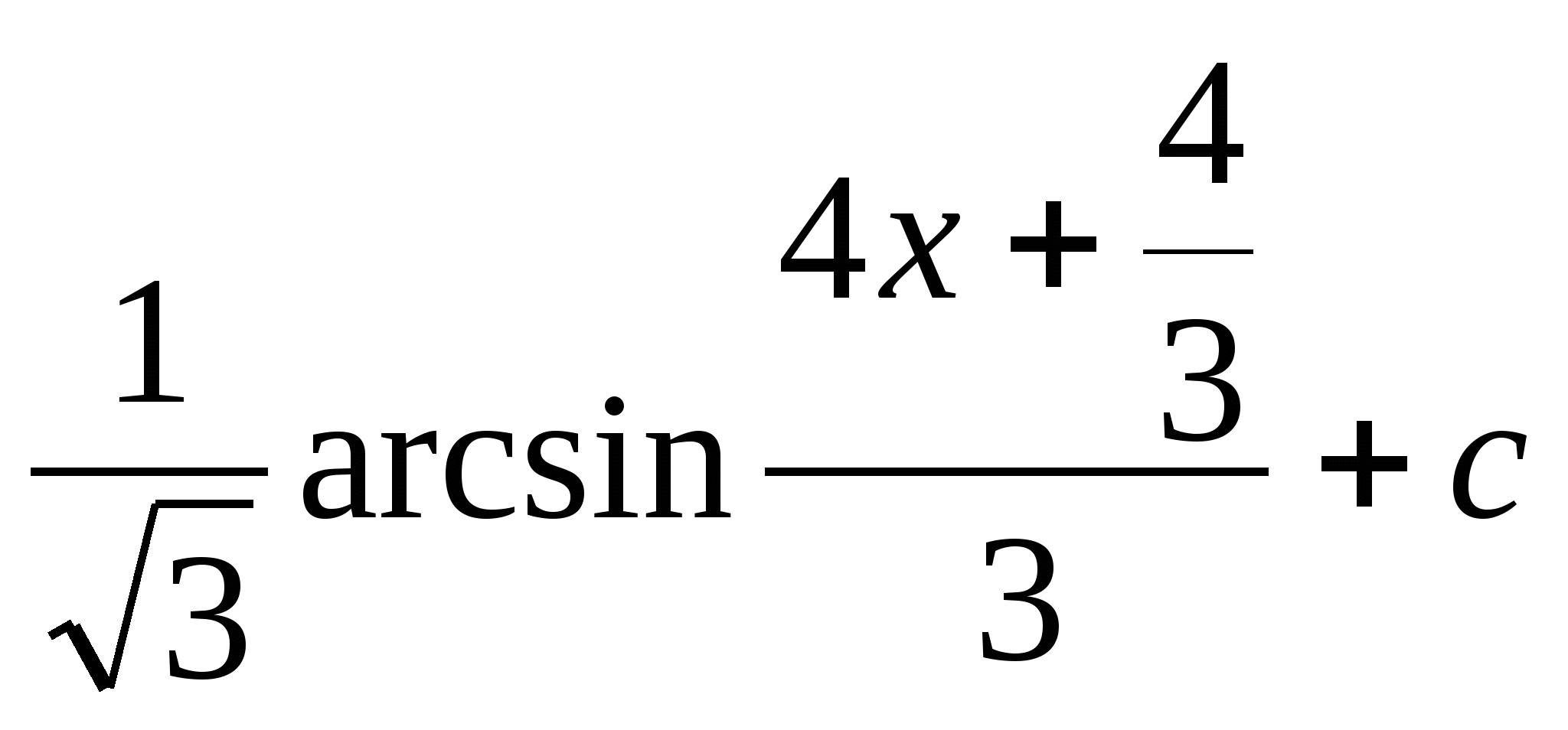
d) 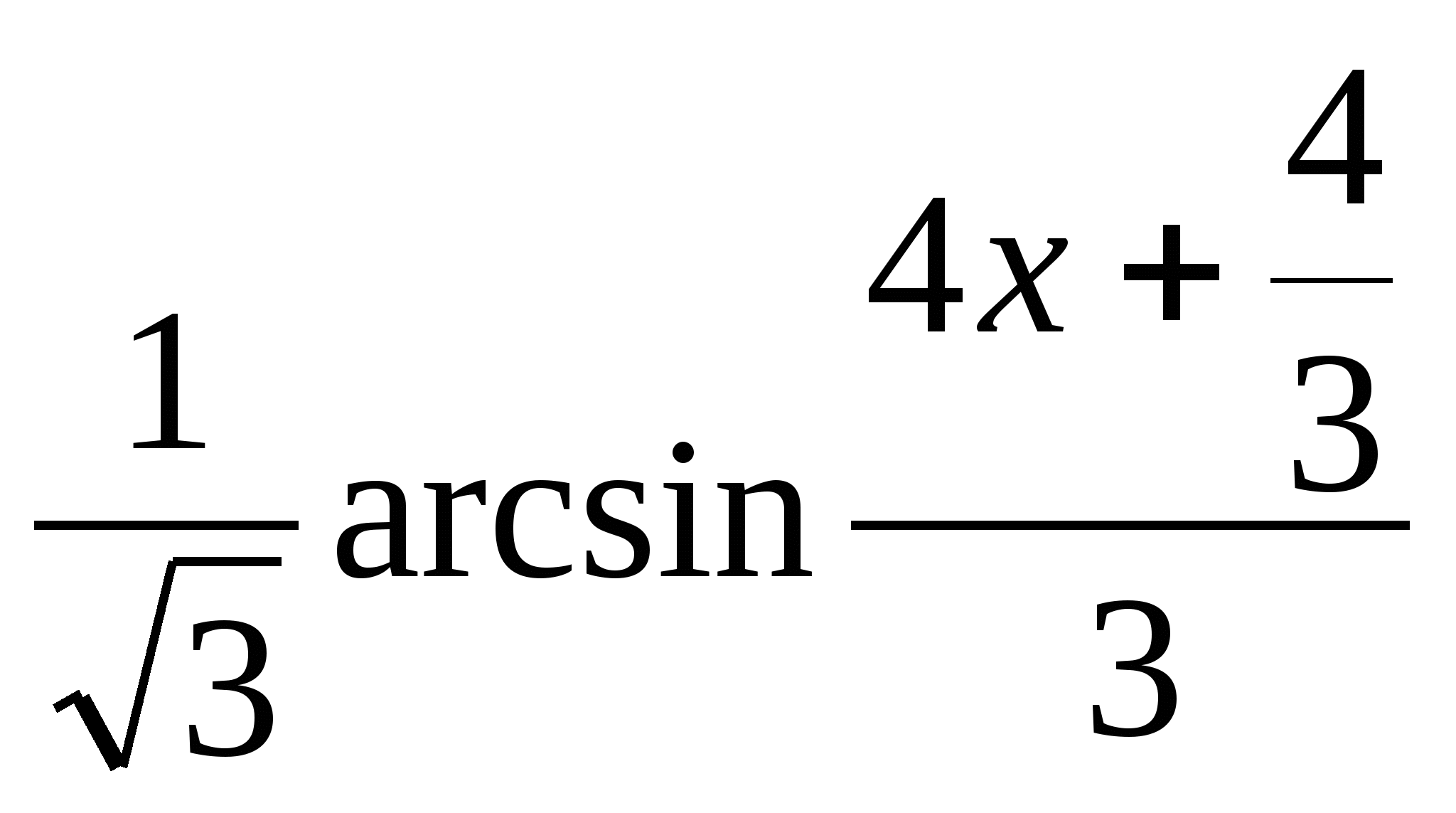
Решение задачи 26.
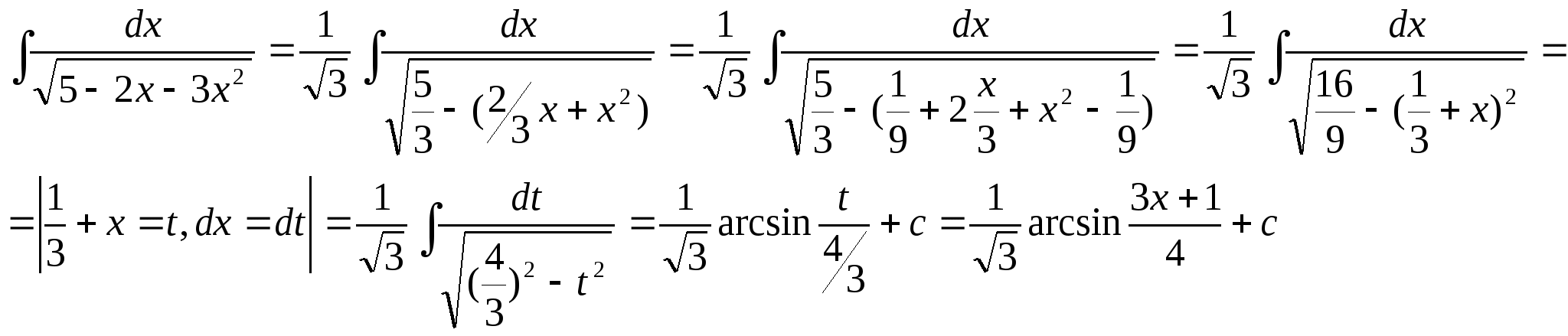
27.Чему равен интеграл ![]() ?
?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 27.
![]()
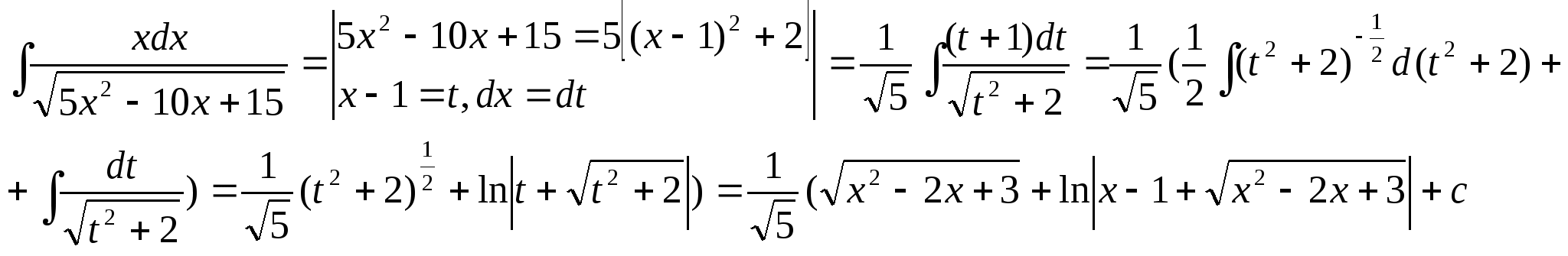
28.Чему равна первообразная ![]() ?
?
a)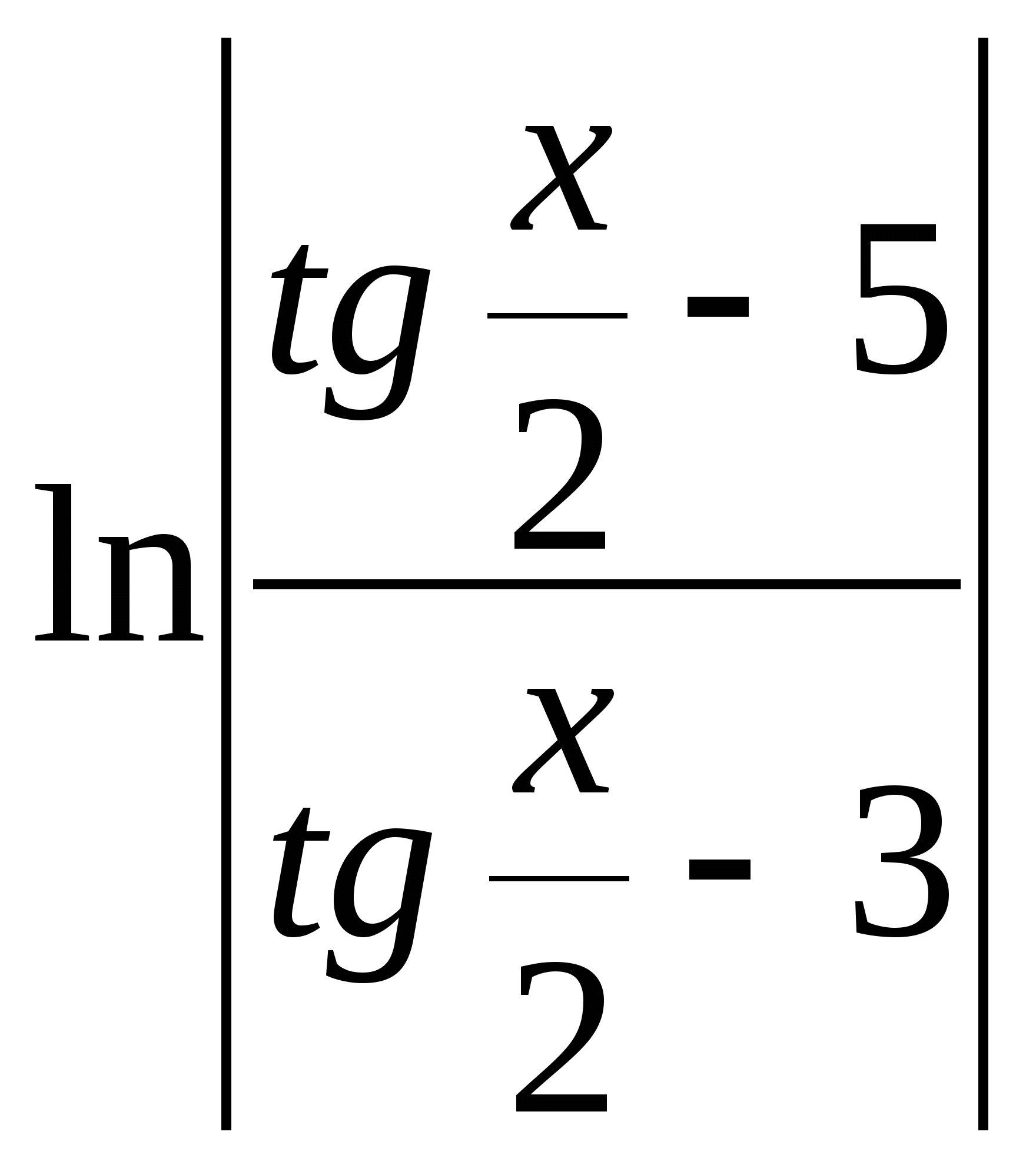 c)
c) 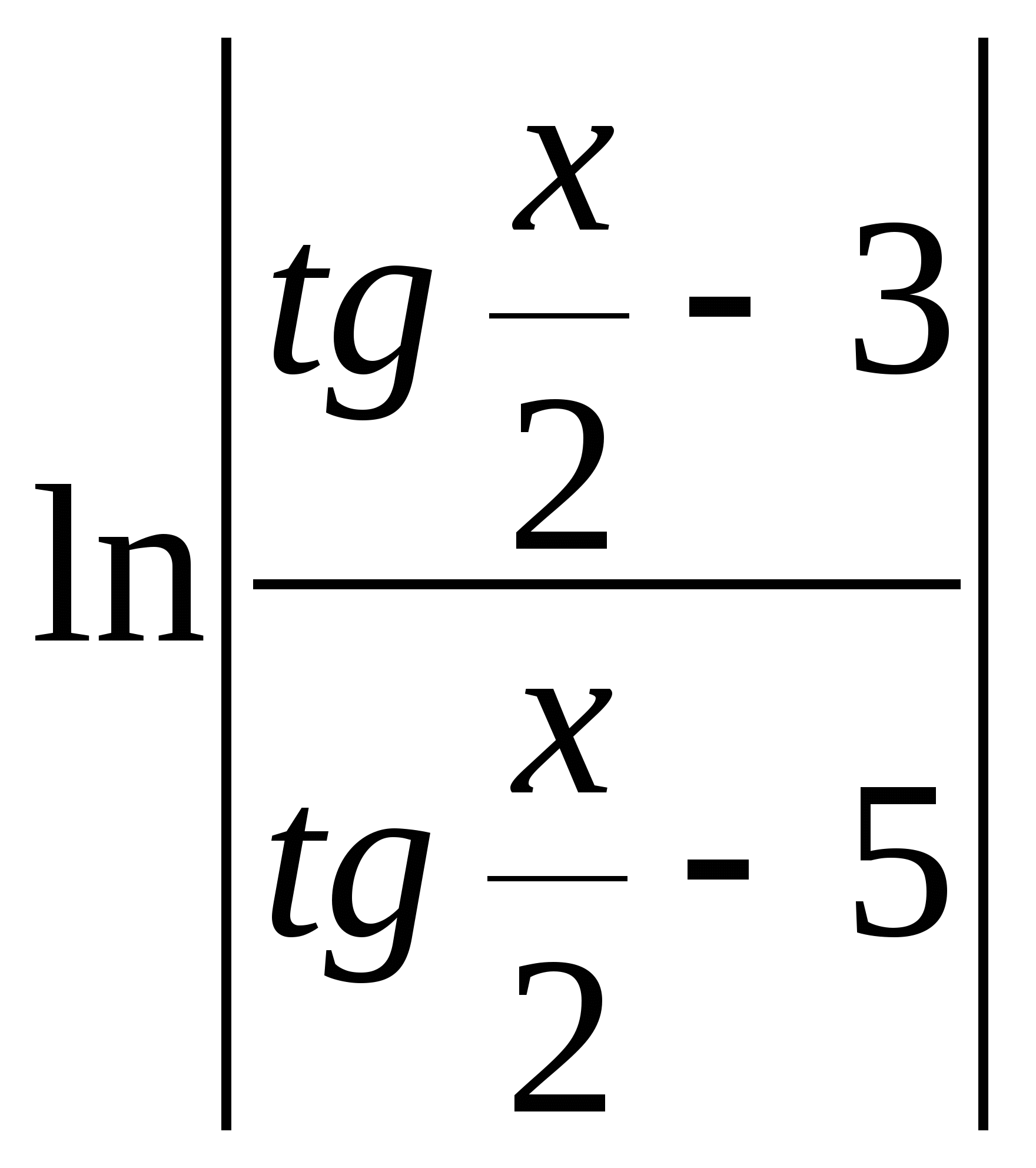
b) 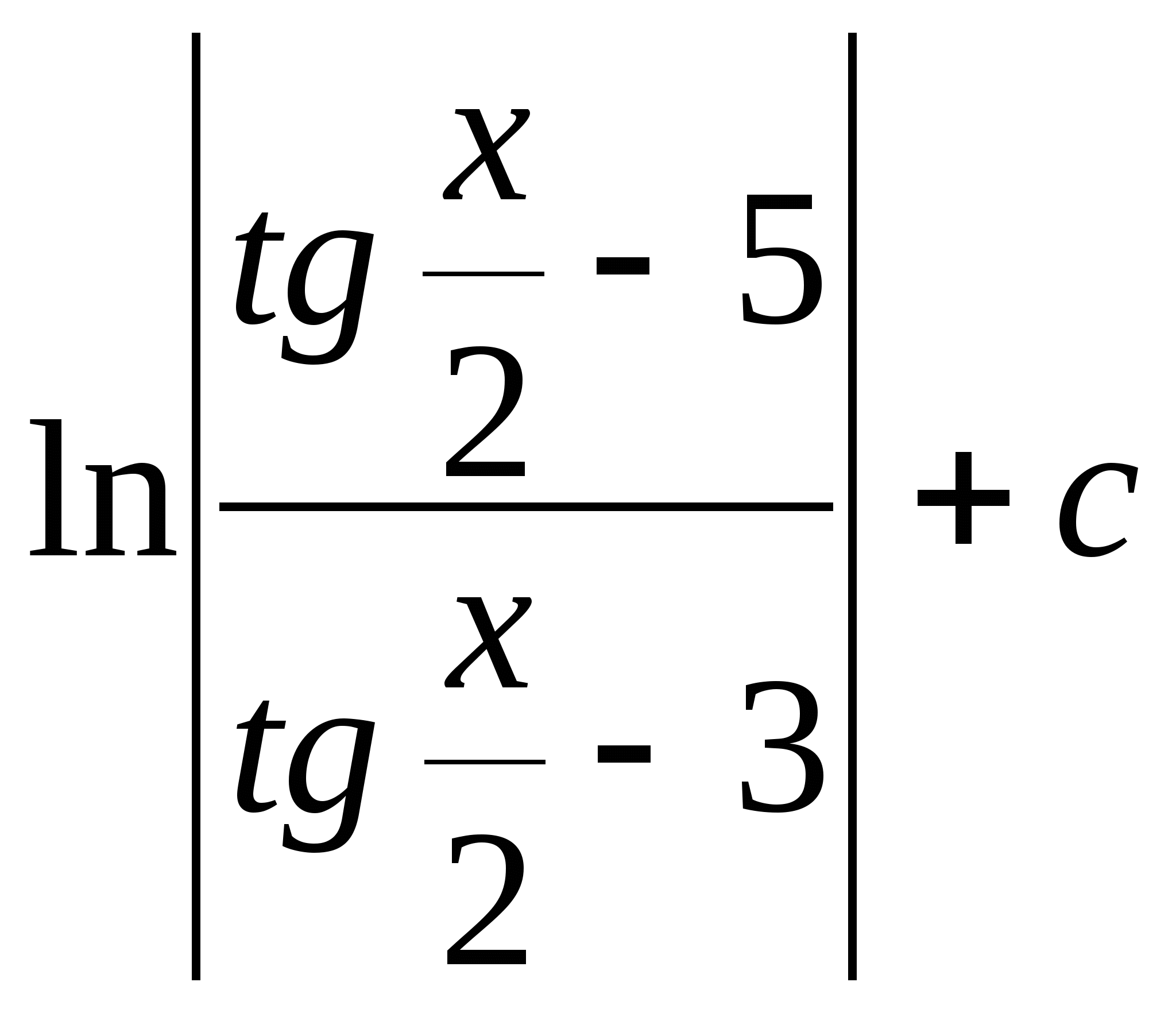 d)
d) 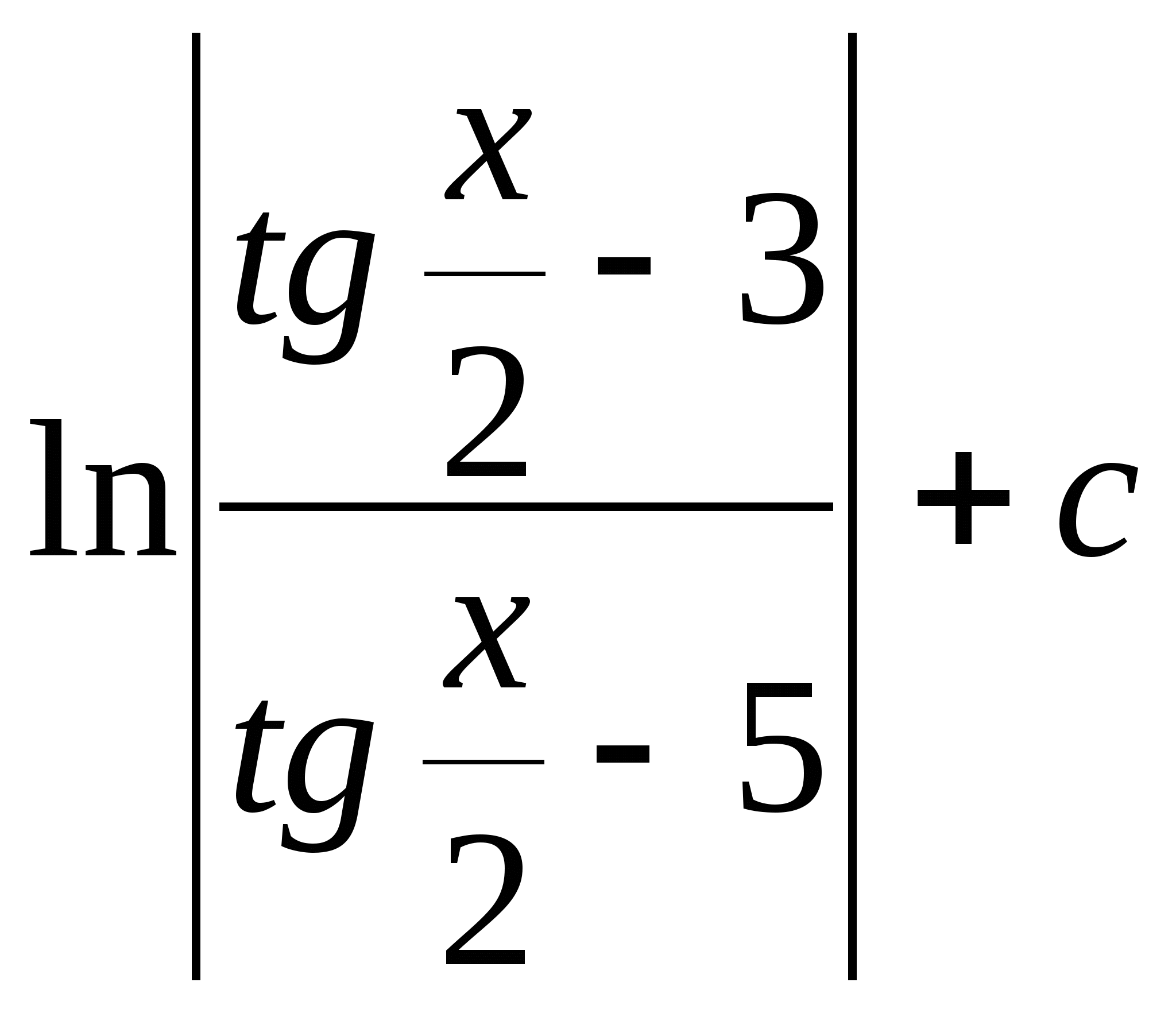
Решение задачи 28.
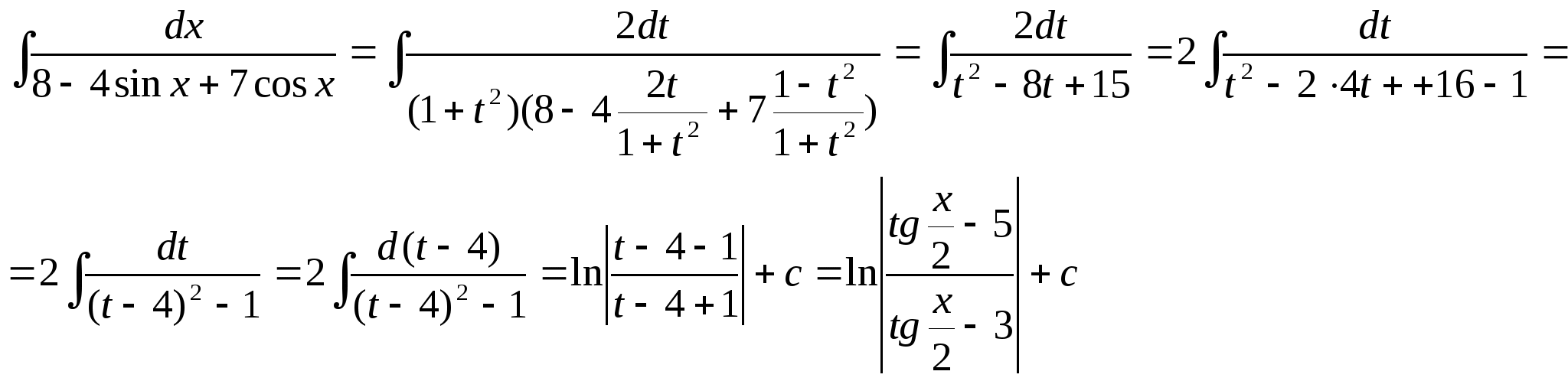
29.Чему равна первообразная ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 29.
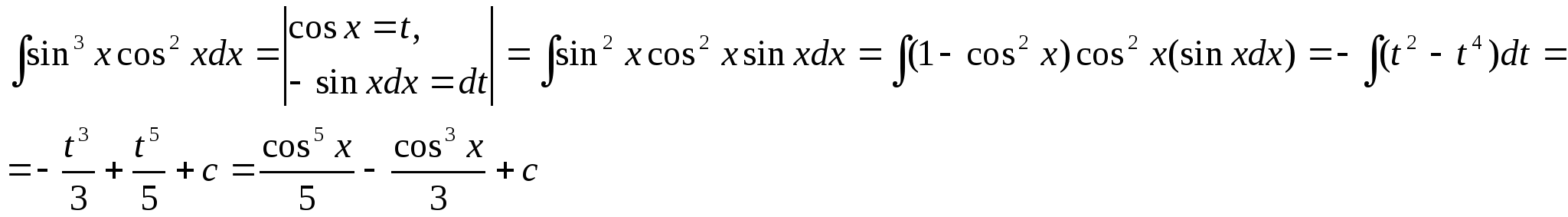
30.Чему равна первообразная ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 30.
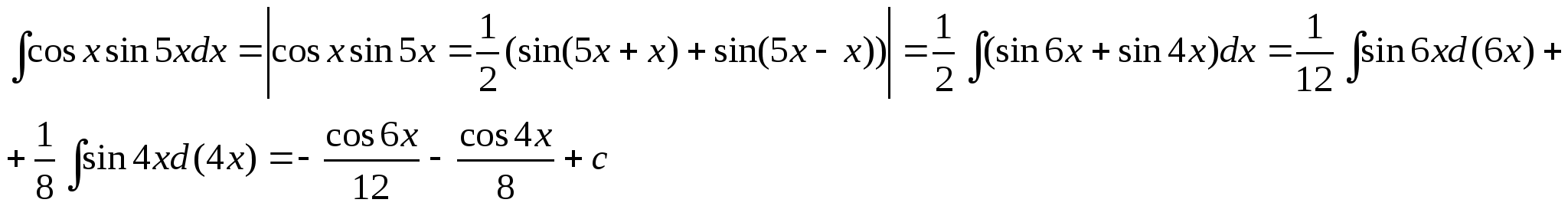
Теория
31. Какая из ниже приведённых формул относится к формуле интегрирования по частям?
a)![]() b)
b)![]()
c) ![]() c)
c)![]()
32. Чему равен интеграл: ![]() ?
?
a)![]() b)
b)![]() c)
c)![]() d )x+c
d )x+c
33. Чему равен интеграл ![]() ?
?
a) sinx+c b)cosx+c c)-sinx d)cosx
34.Закончите теорему: «Если 1. функция x=φ(t) монотонна дифференцируема на (α, β), 2. функция f(x) непрерывна на [а, б], то….»
a)![]()
b)![]()
c)![]()
d)![]()
35. Интегралы вида ![]() называются:
называются:
a) рекуррентными b) циклическими с) определёнными в) неопределёнными
36.Интегралы у которых в процессе применения
формулы ![]()
подынтегральная функция принимает первоначальный вид называются:
a) рекуррентными b) циклическими с) определёнными в) неопределёнными
37.Формула в которой последующий интеграл вычисляется через предыдущий называется:
a) рекуррентной b) циклической с) определённой в) неопределённой
38. Какая из ниже приведённых формул является рекуррентной:
![]()
![]()
c)![]()
![]()
![]()
![]() понижает
порядок k
понижает
порядок k
![]() порядок
k
порядок
k
![]()
d) нет правильного ответа
39.Чему равен интеграл ![]() ?
?
a)![]() c)
c)![]()
40. Операция отыскания первообразной называется:
a) интегрированием b)дифференцированием
с) a) и b) верно в) нет правильного ответа
Рациональные дроби. Тригонометрические функции. Иррациональности
41.![]() dx
dx
a)![]()
b)![]()
c)![]()
d)![]()
Решение задачи 41.
f(x) - неправильная рациональная дробь.
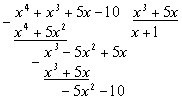
![]() ;
;
![]() ,
, ![]()
![]()
![]() =>A=2,
B=3, C=0.
=>A=2,
B=3, C=0.
![]()
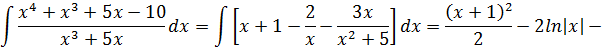
![]()
42. ![]()
a)![]()
b)![]()
c)![]()
d)нет правильного ответа
Решение задачи 42.
F(x) - правильная рациональная дробь. Корни знаменателя: x=0, x=2, x=-2.
![]() ;
;
![]()
![]()
x3: A+C+D=0,
x2: B+2C-2D=1, => ![]()
x1: -4A=6,
x0: -4B=-12
Подставив корни ![]() в уравнение (*), найдём С и D:
в уравнение (*), найдём С и D: ![]()
![]()
![]() =
=![]() .
.
43.Чему равен интеграл ![]() ?
?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 43.
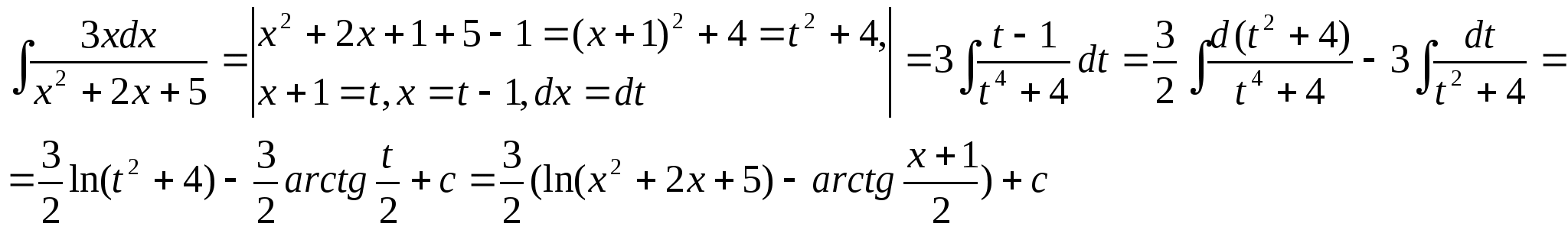
44.Чему равен интеграл ![]() ?
?
a)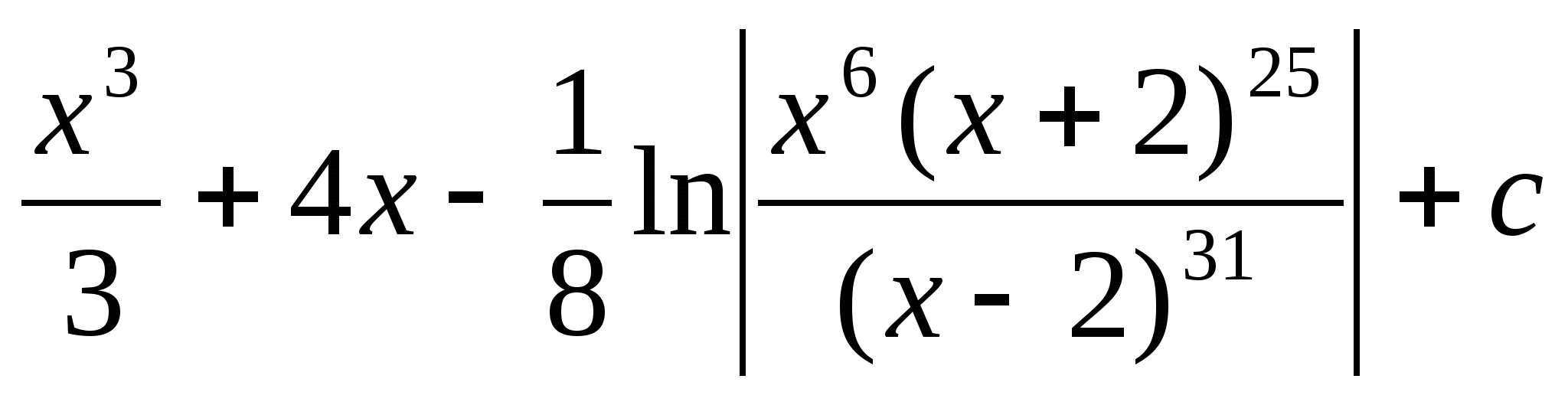
b) 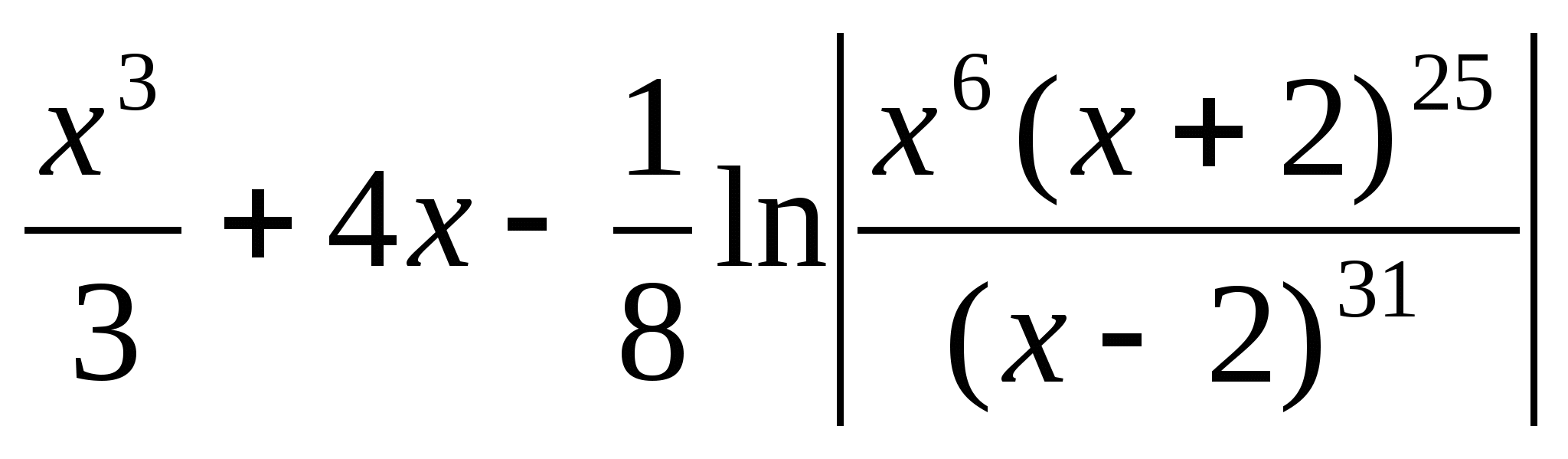
c) 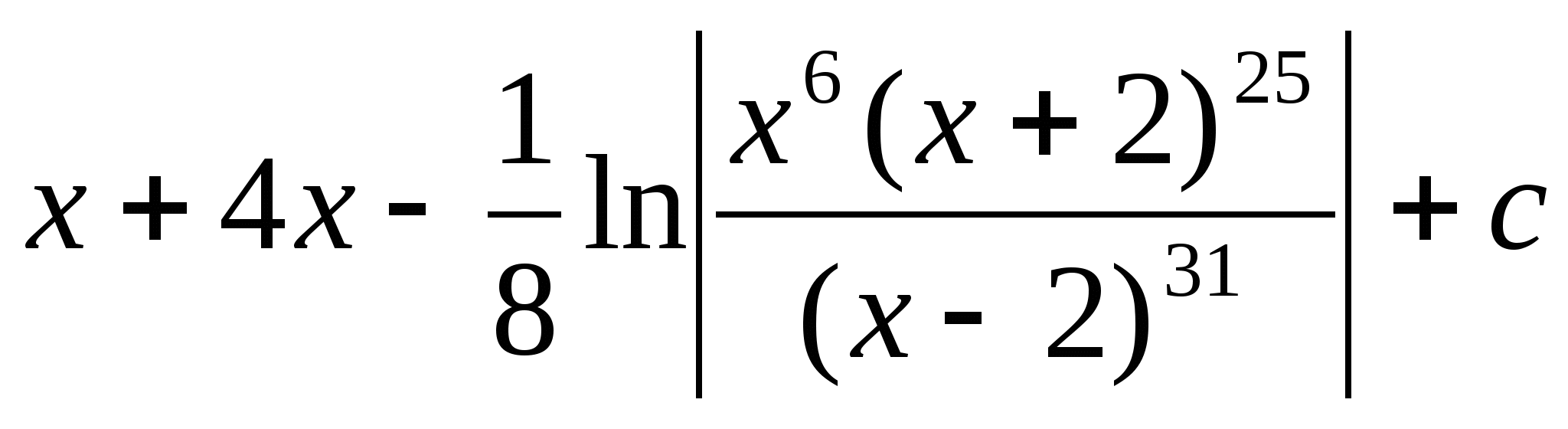
d) 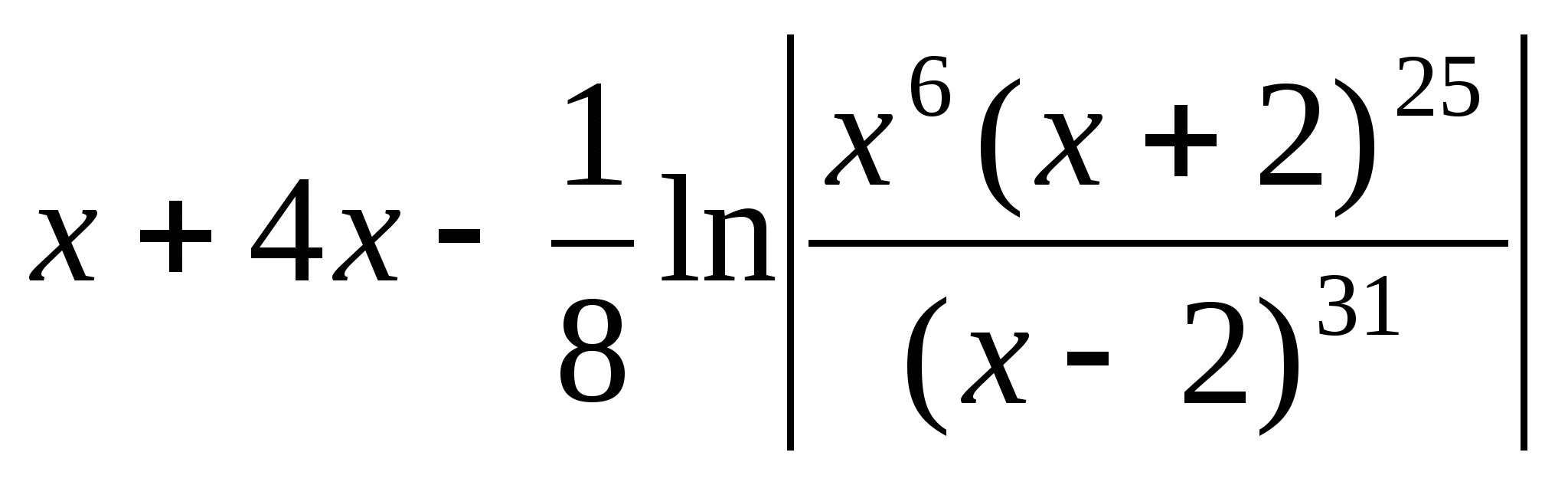
Решение задачи 44.
Дробь рациональная, неправильная. Делим
![]() (уголком):
(уголком):
Получаем ![]()
Последняя дробь правильная, её знаменатель имеет корни:
![]()
Приводим правую часть равенства к общему знаменателю и приравниваем числители левой и правой дробей:
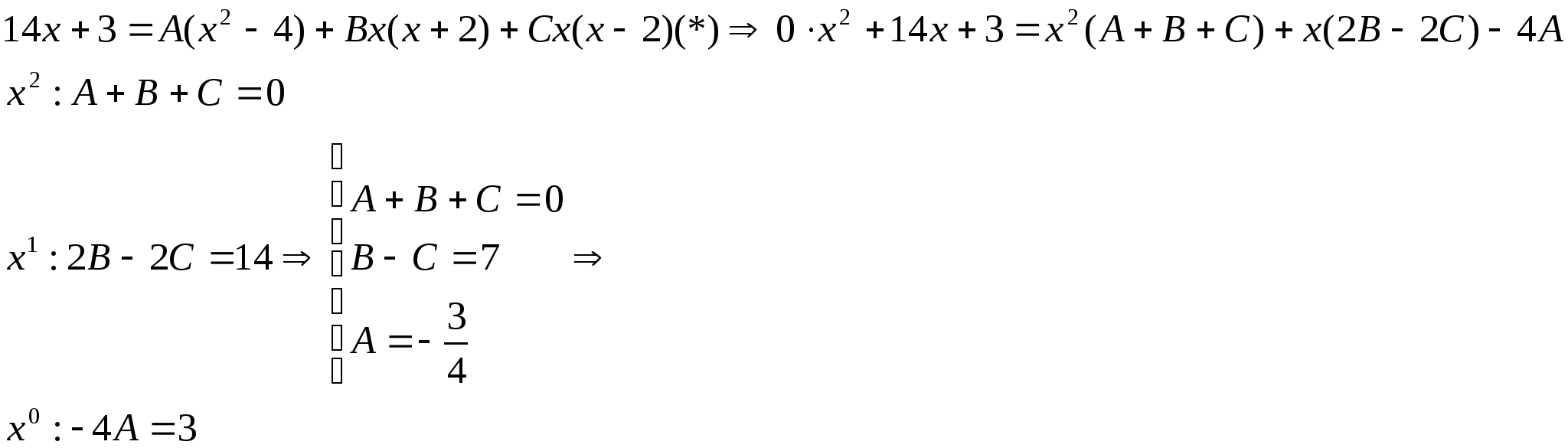
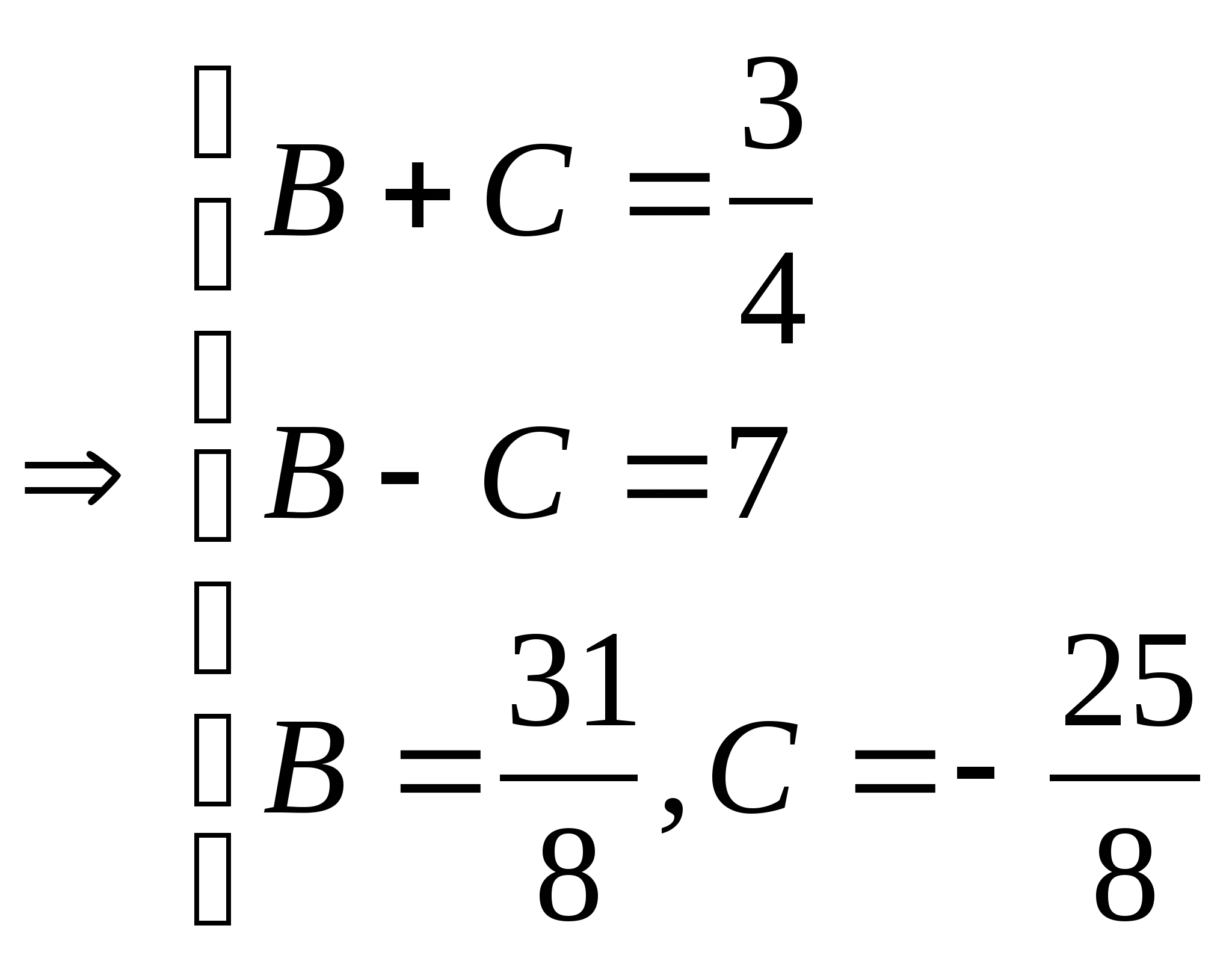
Можно найти коэффициенты, не составляя системы, а подставляя корни знаменателя в равенство (*):
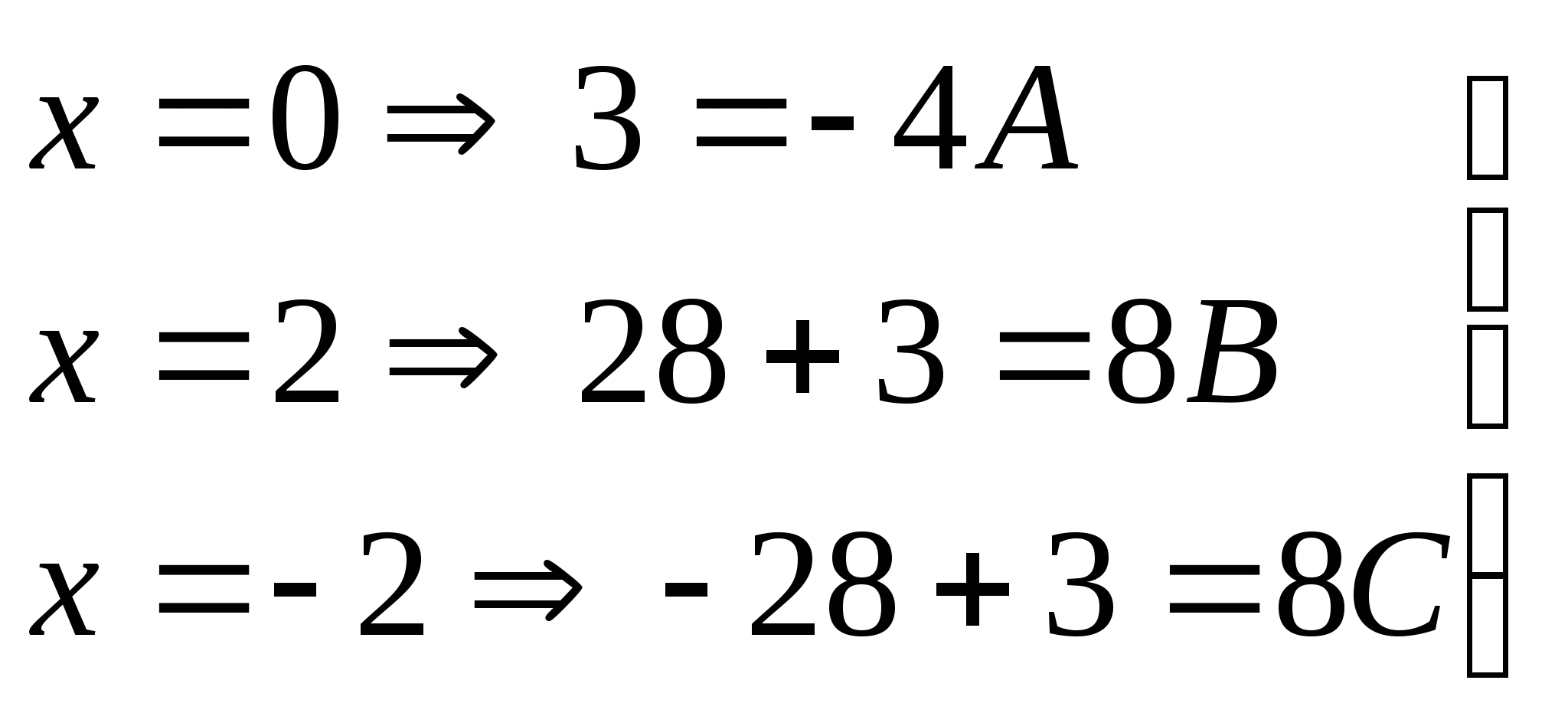
Вернёмся к исходному интегралу: ![]()
![]()
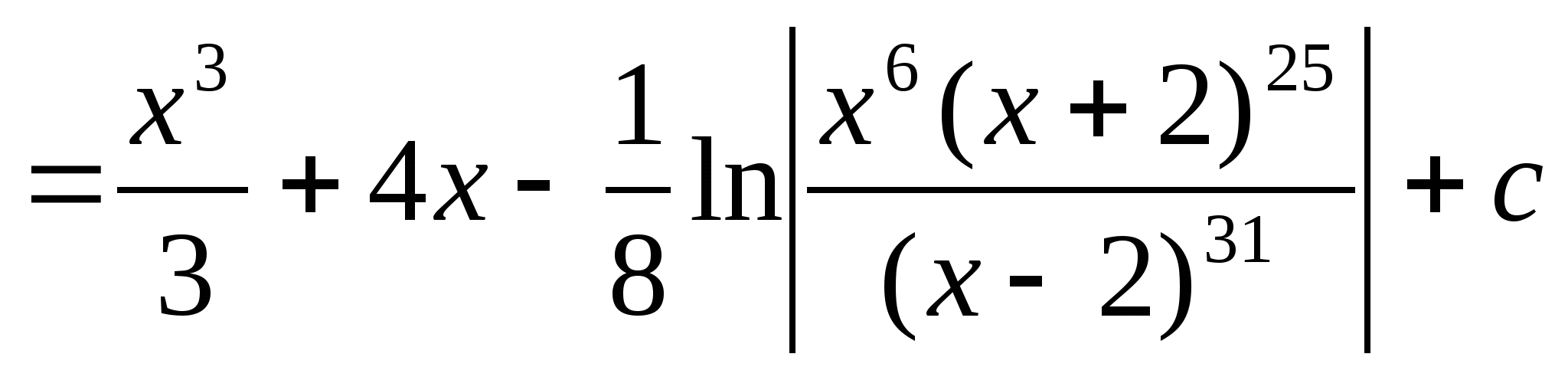
45.![]()
a)![]() b)
b)![]()
c)![]() d) нет правильного ответа
d) нет правильного ответа
Решение задачи 45.
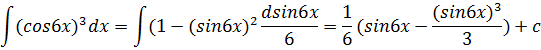
46.![]()
a)![]() b)
b)![]()
c)![]() c)нет правильного ответа
c)нет правильного ответа
Решение задачи 46.
Используем формулу: ![]()
![]()
47.![]()
a)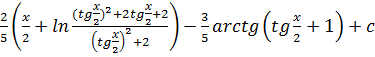
b)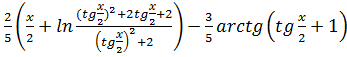
c)![]()
d)нет правильного ответа.
Решение задачи 47.
Выполняем подстановку: ![]()
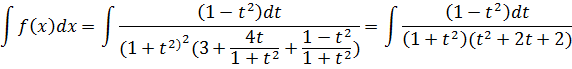
Правильную рациональную дробь разлагаем на сумму простых дробей:
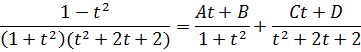
![]()
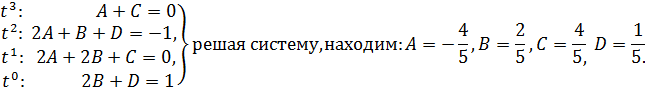
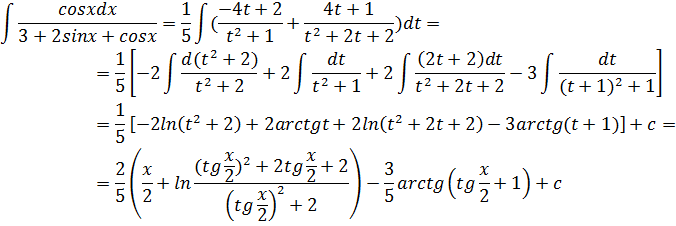
48.![]()
a)![]() b)
b)![]()
c)![]() d)
d)![]()
Решение задачи 48.
![]()
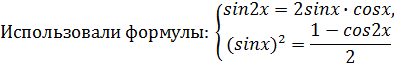
49.![]()
a) ![]() b)
b)![]()
c) ![]() d )
d ) ![]()
Решение задачи 49.
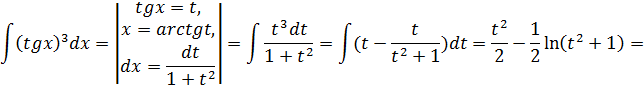
![]()
![]()
50.Чему равен интеграл ![]() ?
?
a)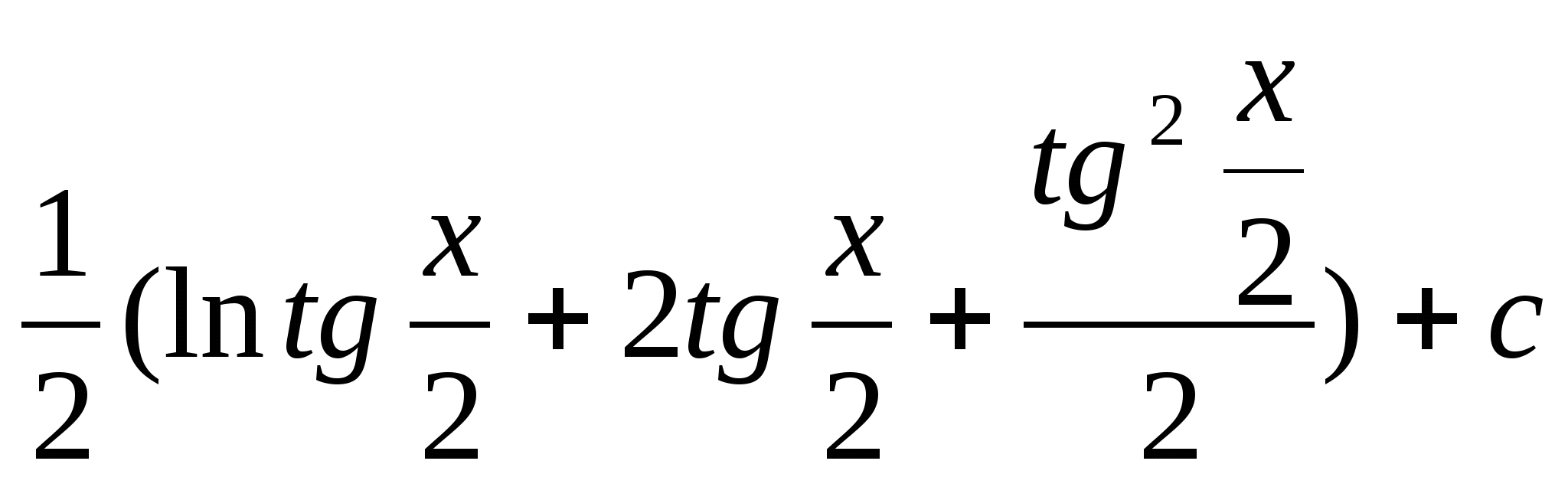
b) 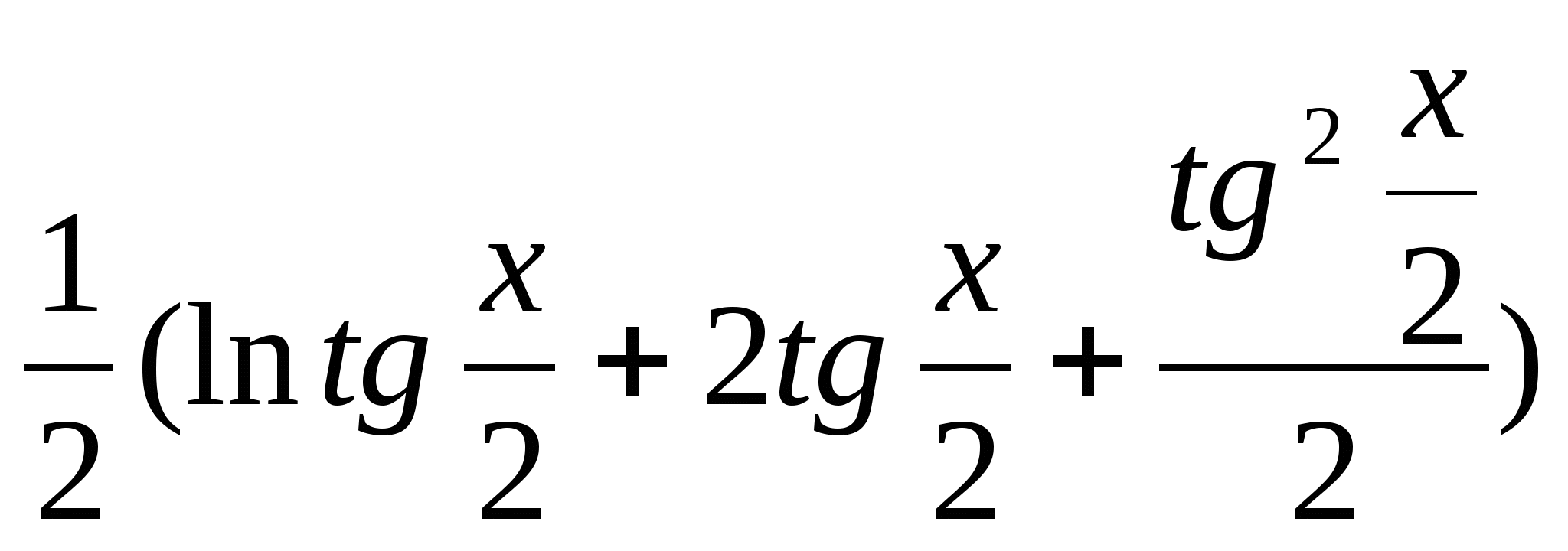
c) ![]()
d) ![]()
Решение задачи 50.
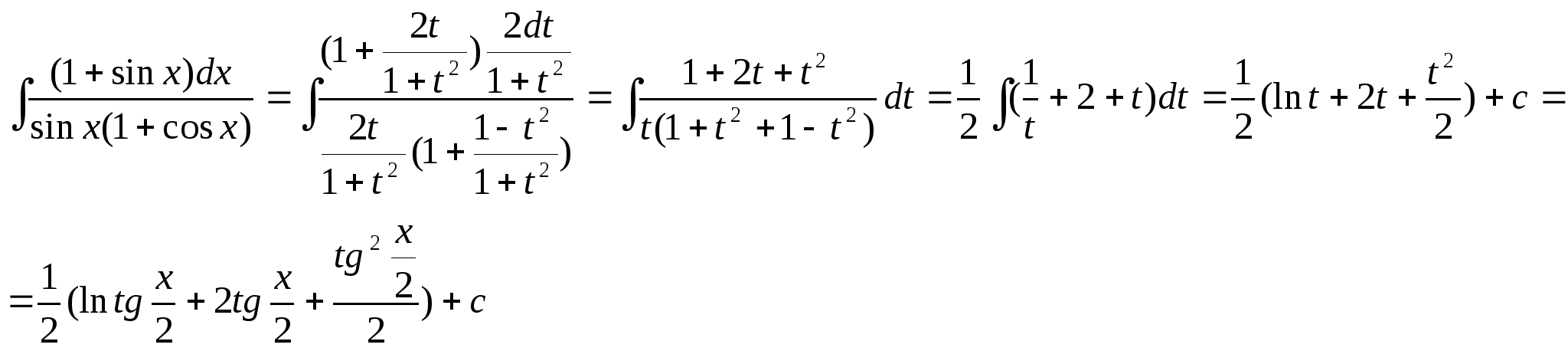
51.Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 51.
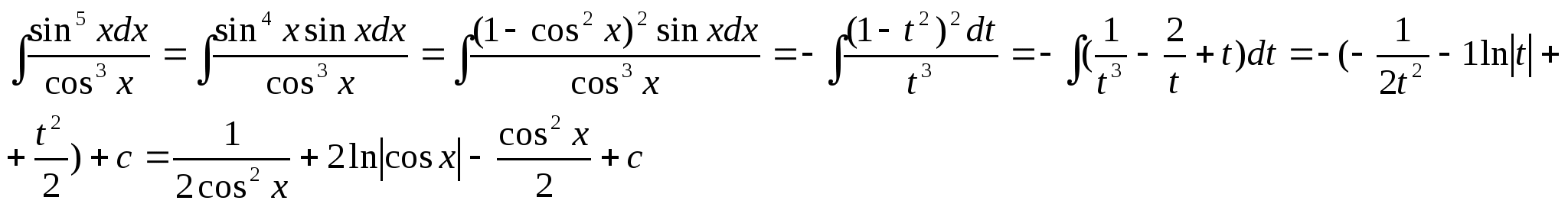 52.Чему
равен интеграл
52.Чему
равен интеграл ![]() ?
?
a)![]()
b)![]()
c) ![]()
d) ![]()
Решение задачи 52.
![]()
![]()
![]()
53.Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c)![]()
d) ![]()
Решение задачи 53.
![]()
![]()
![]()
54. Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 54.
![]()
55. Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c) ![]()
d) ![]()
Решение задачи 55.
![]()
56. ![]()
a)![]() b)
b)![]()
c)![]() d)
d)![]()
Решение задачи 56.
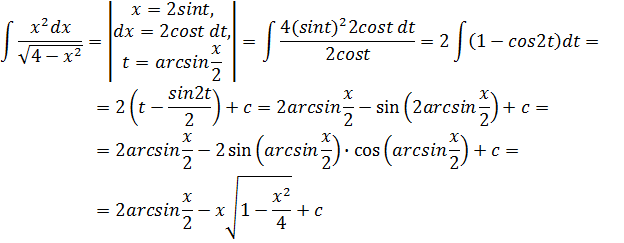
57.![]()
a)![]() b)
b)![]()
c)![]() d)нет правильного ответа
d)нет правильного ответа
Решение задачи 57.
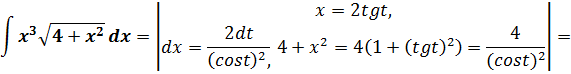
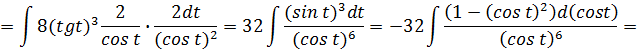
![]()
![]()
58.![]()
a)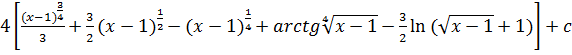
b)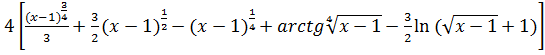
c)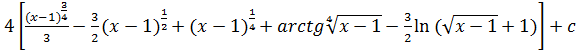
d)нет правильного ответа
Решение задачи 58.
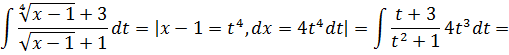
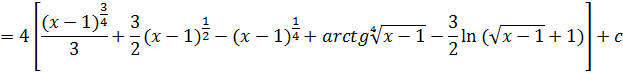
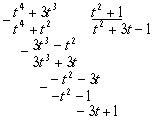
59.![]()
a)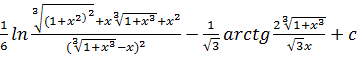
b)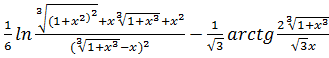
c)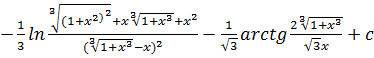
d)нет правильного ответа
Решение задачи 59.
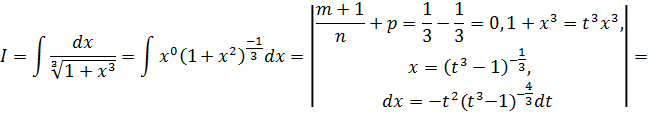
![]()
Корни знаменателя: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
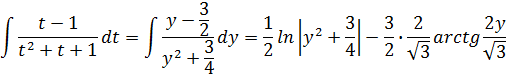
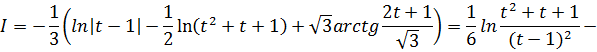
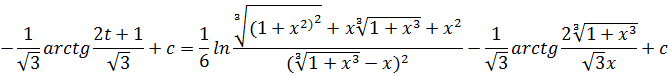
60. Чему равен интеграл ![]() ?
?
a)![]()
b) ![]()
c)![]()
d) ![]()
Решение задачи 60.
Запишем стандартную форму дифференциального бинома:
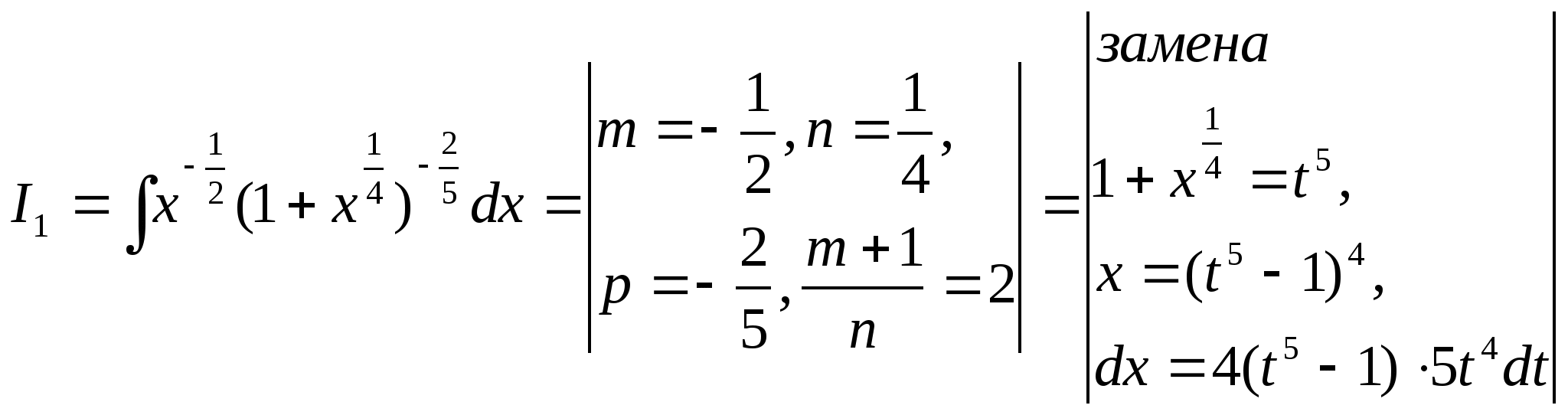
![]()
![]()
Приближённые методы. Определённый интеграл.
Задачи, приводящие к понятию определённого интеграла: о площади трапеции.
Свойства определённого интеграла.
a)![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 61.
Функция ![]() непрерывна всюду. Преобразуем её:
непрерывна всюду. Преобразуем её:
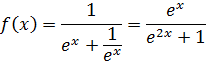
Вычисляем определённый интеграл:
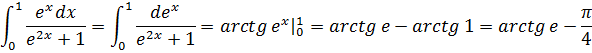
a)![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 62.
Функция ![]() непрерывна всюду.
непрерывна всюду.
Вычисляем определённый интеграл, понижая порядок
функции по формулам: ![]() :
:
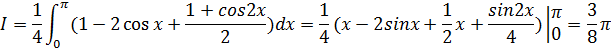
![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 63.
Функция ![]() непрерывна на промежутке интегрирования.
непрерывна на промежутке интегрирования.
Делаем замену: ![]()
Пределы интегрирования: если х=0, t=0, если
x=ln2, ![]()
Вычисляем определённый интеграл:
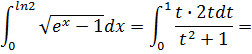
Получили неправильную рациональную дробь. Для выделения целой части применим искусственный приём: добавим единицу и вычтем единицу в числителе, а затем поделим почленно числитель на знаменатель:
![]()
![]()
a)10 b)-5 c)-10 d)5
Решение задачи 64.
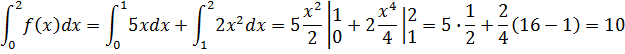
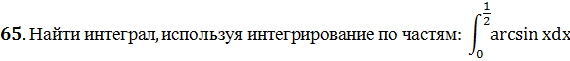
a)![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 65.
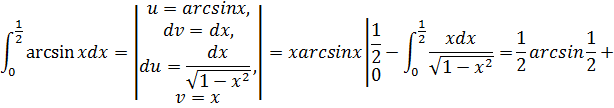
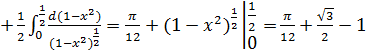
66. Найти интеграл используя замену переменной:
![]()
a)- ![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 66.
![]()
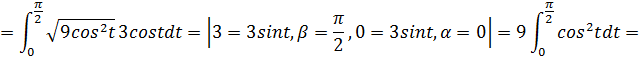
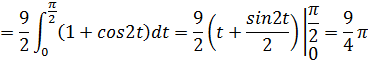
Теория
67. Чему равна площадь криволинейной трапеции приближённо?
a) сумме площадей построенных прямоугольников;
b) сумме площадей построенных трапеций;
c)разности площадей построенных прямоугольников;
d) разности площадей построенных трапеций.
68.Какая из ниже приведённых формул является формулой для нахождения площади криволинейной трапеции?
a)![]()
b)![]()
c) ![]()
d)
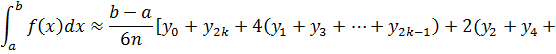
![]()
69. Как называется ниже приведённая формула?
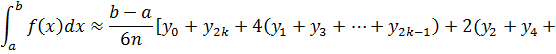
![]()
-
Формулой Симпсона
-
Формулой трапеции
-
Формулой прямоугольников
-
Нет правильного ответа
70. Закончите теорему:
Производная от определённого интеграла с переменным верхним пределом по переменному пределу равна подынтегральной функции …. .
-
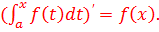
-
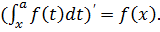
-
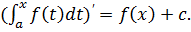
-
Нет правильного ответа
71. Какая из ниже приведённых формул относится к формуле интегрирования по частям в определённом интеграле:
a) ![]()
b)![]()
c)![]()
d)![]()
72. Чему равен интеграл ![]()
a) a-b b)0 c)b-a d)x
73.Как называется ниже приведённая теорема?
Если функция f(x) непрерывна на ![]() , m и M соответственно её наименьшее и наибольшее значения на
, m и M соответственно её наименьшее и наибольшее значения на
![]() , то
, то
![]() .
.
a)Теорема о среднем
b) Теорема об оценке определённого интеграла
с)Основная формула интегрального исчисления
d)Теорема Ньютона-Лейбница
74.Чему равен интеграл ![]()
a)0 b)1 c)a-b d)-f(x)
75. Как называется ниже приведённая теорема?
Если функция f(x) непрерывна ![]() ,то найдётся точка
,то найдётся точка ![]() такая что
такая что ![]()
a)Теорема о среднем
b) Теорема об оценке определённого интеграла
с)Основная формула интегрального исчисления
d)Теорема Ньютона-Лейбница
76. Формула Ньютона-Лейбница служит для вычисления:
a) неопределённых интегралов
b) определённых интегралов
с) неопределённых и определённых интегралов
d)нет правильного ответа
77.![]()
a)![]()
b)![]()
c)![]()
d)![]()
78.Теорема ![]() называется
называется
a)Теорема о среднем
b) Теорема об оценке определённого интеграла
с)Основная формула интегрального исчисления
d)Теорема Ньютона-Лейбница
Вычисление площадей с помощью определённого интеграла в декартовой системе координат.
Вычисление длины дуги.
Вычисление объёма методом параллельных сечений. Объём тела вращения.
Несобственные интеграла.
-
Чему равна площадь фигуры, ограниченной синусоидой
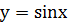 и центральной ветвью тангенсоиды
и центральной ветвью тангенсоиды 
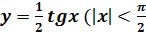
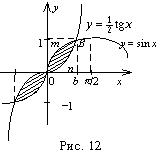
a)![]() b)ln2 c)lne d)
b)ln2 c)lne d)![]()
Решение задач 79.
Фигура, ограниченная заданными кривыми, состит из двух «лепестков», симметричных относительно начала координат, поэтому можно найти площадь одного лепестка и результат удвоить. Площадь области OmBn найдём как разность площадей трапеций OmBb и OnBb. Найдём точки пересечения линий, решив систему уравнений:
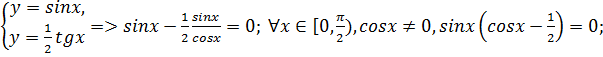
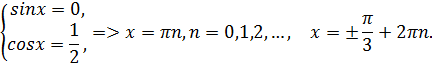
Учитывая условия задачи, выбираем: ![]()
Итак: 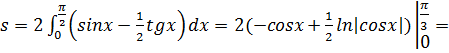
![]()
![]() .
.
80.Чему равна площадь области, ограниченной
эллипсом ![]() ?
?
а)![]() b)
b)![]() c)
c)![]() d)
d)![]()
Решение задачи 80.
В силу симметрии области достаточно найти площадь четвёртой части области, например, расположенную в первой четверти. Полученную величину затем умножить на 4.
Для вычисления площади удобнее уравнение эллипса представить в параметрической форме
![]() (в
первой четверти
(в
первой четверти ![]()
Пределы интегрирования для переменной t:
![]()
![]()
Итак:
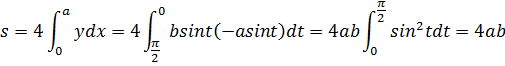
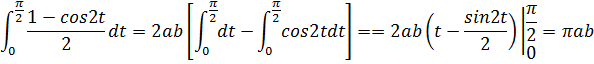
81.Чему равна площадь, ограниченной петлёй декартова листа
![]()
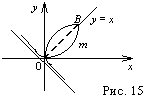
a)![]() b) -
b) -![]() c)
c) ![]() d)
d) ![]()
Решение задачи 81.
Запишем уравнение кривой в полярной системе
координат, используя формулы перехода ![]()
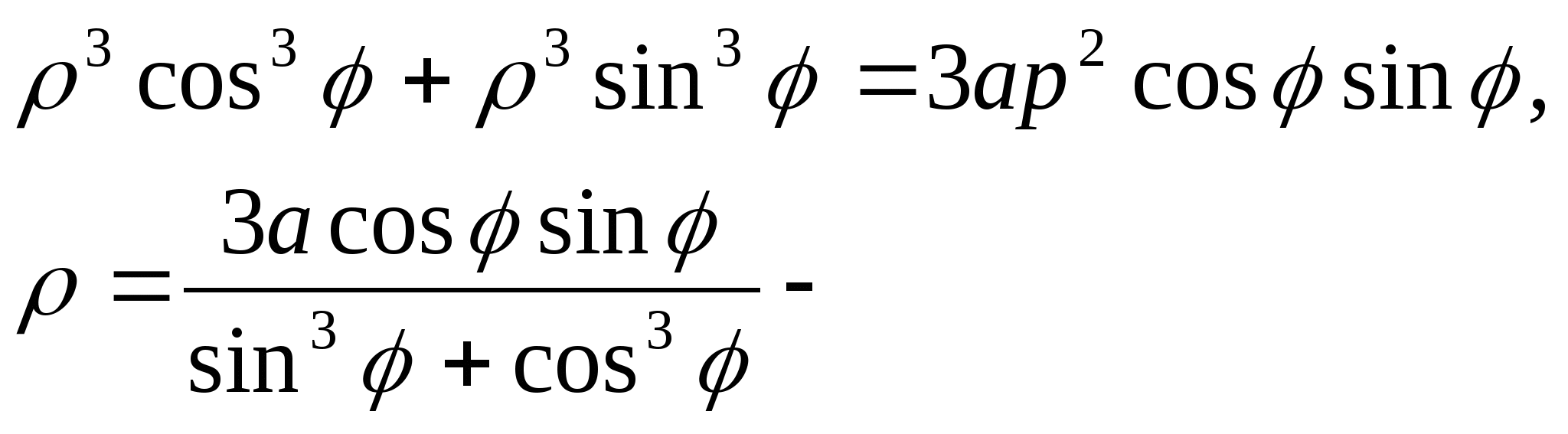
- уравнение кривой в полярных координатах.
Кривая симметрична относительно биссектрисы
первого координатного угла y=x (замена переменных х на у и у на х
не изменяет уравнения), поэтому найдём площадь половины лепестка и
результат удвоим. Если радиус-вектор описывает дугу ОmB, угол φ
изменяется от 0 до ![]() .
.
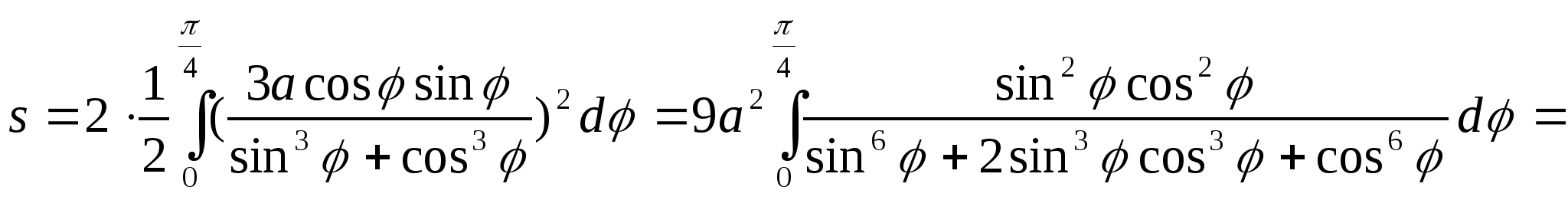
(Разделим числитель и знаменатель на ![]() )=
)=
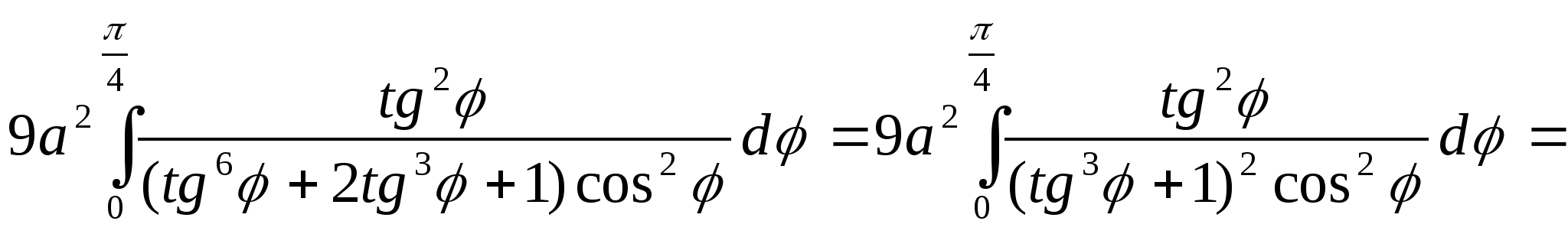
Замена переменной
![]()
![]() новые
пределы
новые
пределы ![]()
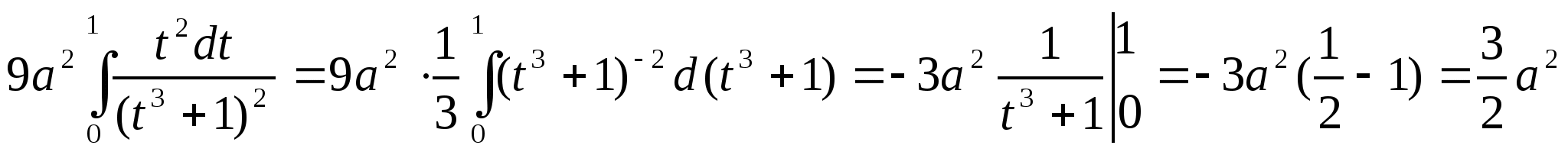
82.Чему равна длина дуги полукубической параболы
![]() заключённой между точками О(о,о) и А(5,
заключённой между точками О(о,о) и А(5, ![]() ).
).
a)![]() b) -
b) -![]() c)
c) ![]() d)
d) ![]()
Решение задачи 82.
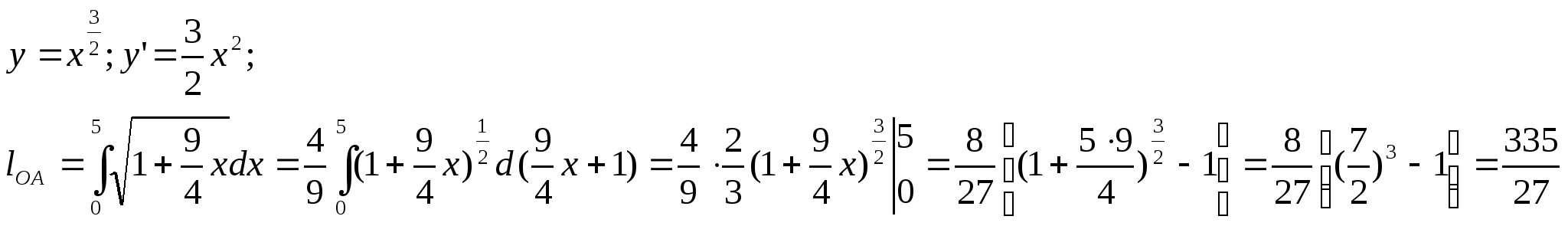 83.
Чему равна длина дуги астроиды
83.
Чему равна длина дуги астроиды ![]()
a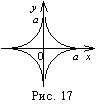 )6a
b)-6a b)0 c)-3a
)6a
b)-6a b)0 c)-3a
Решение задачи 83.
Воспользуемся симметрией кривой и найдём длину дуги, расположенной в первой четверти, затем умножим на 4 полученную величину:
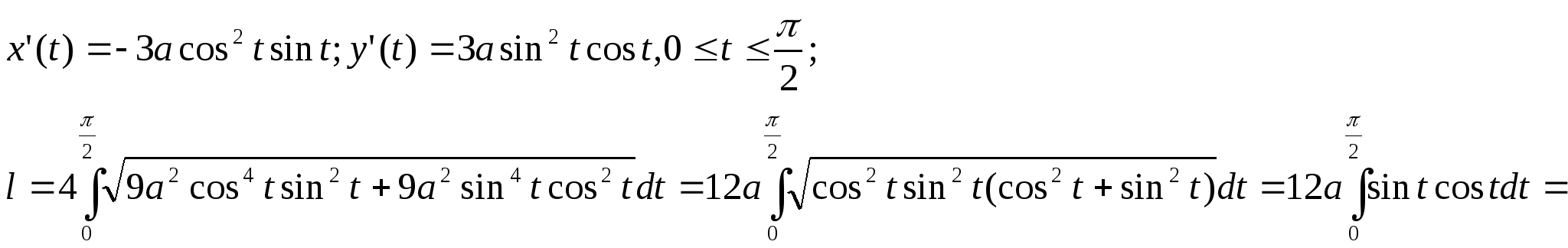
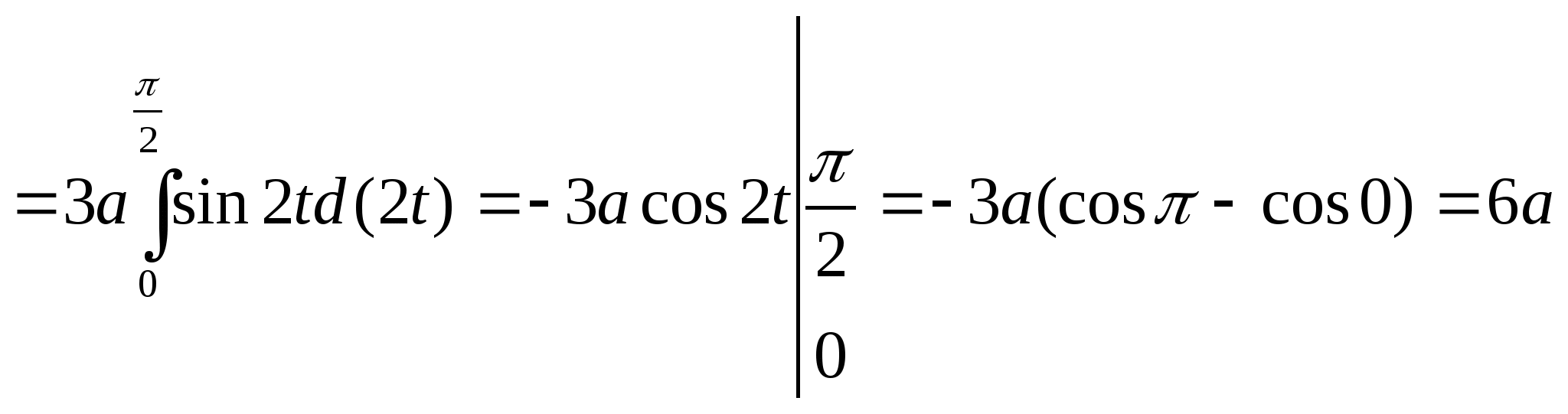
84.Чему равна длина кривой ![]() при изменении угла
при изменении угла ![]() от 0 до
от 0 до![]() ?
?
a)![]() b)-
b)-![]() c)
c) ![]() d)-
d)-![]()
Решение задачи 84.
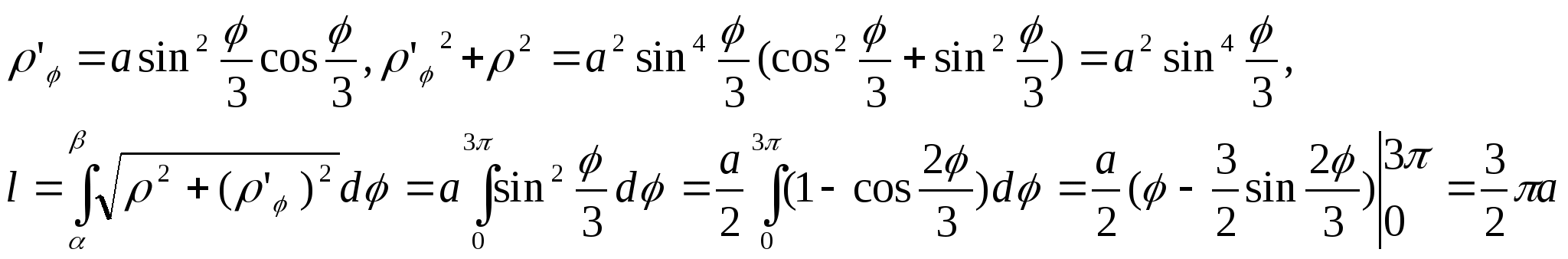
85.Чему равен объём шара радиуса r?

a)![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Решение задачи 85.
Будем рассматривать шар как тело, образованное
вращением полуокружности ![]() вокруг оси Ох.
вокруг оси Ох.
Центр окружности - в начале координат, следовательно, a=-r, b=r.
Для вычисления объёма шара воспользуемся формулой
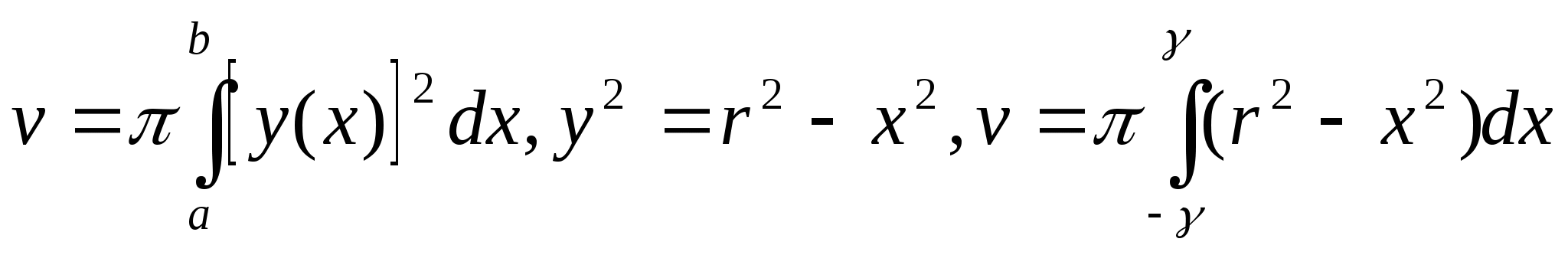
Используем чётность функции на симметричном интервале:
![]()
86.Чему равен интеграл ![]() ?
?
a)![]() b)0 c)
b)0 c)![]() d)
d) ![]()
Решение задачи 86.
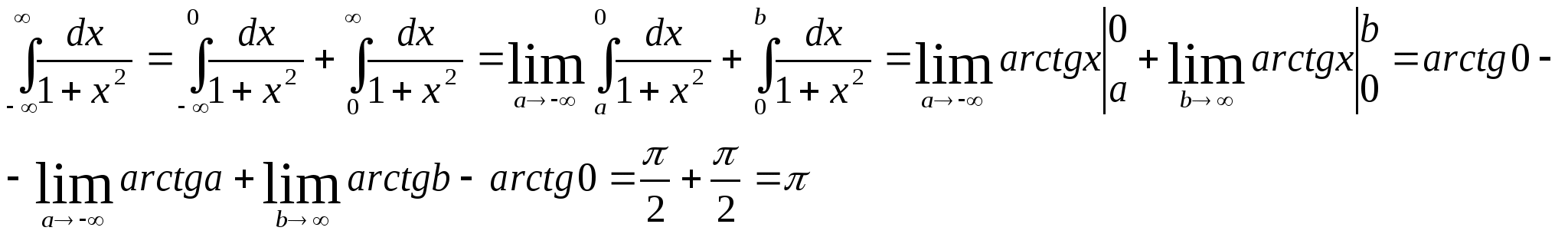
87.Чему равен интеграл 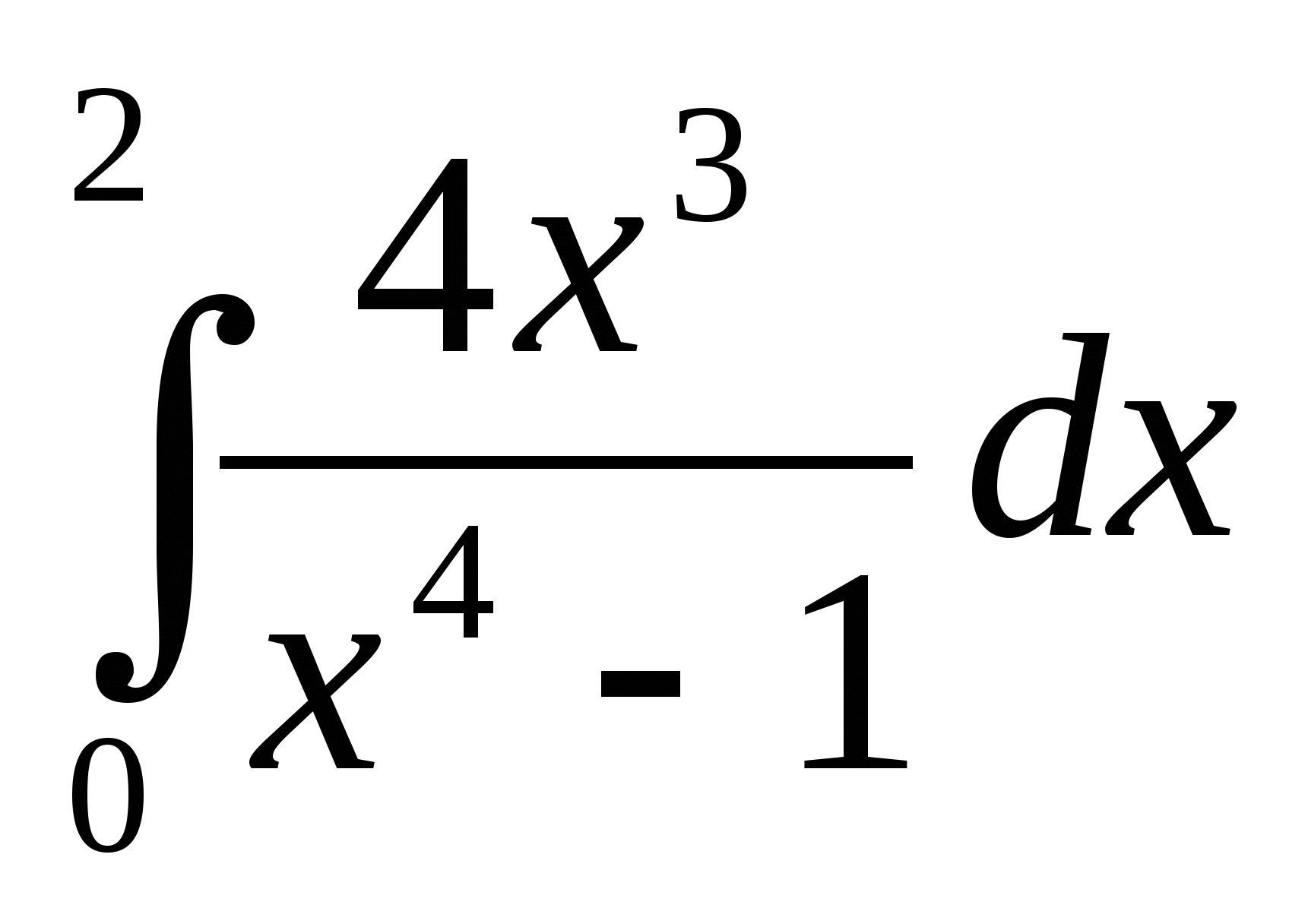 ?
?
a)![]() b)
b) ![]() c)0 d)нет правильного ответа
c)0 d)нет правильного ответа
Решение задачи 87.
В точке x=0 функция ![]() терпит бесконечный разрыв.
терпит бесконечный разрыв.
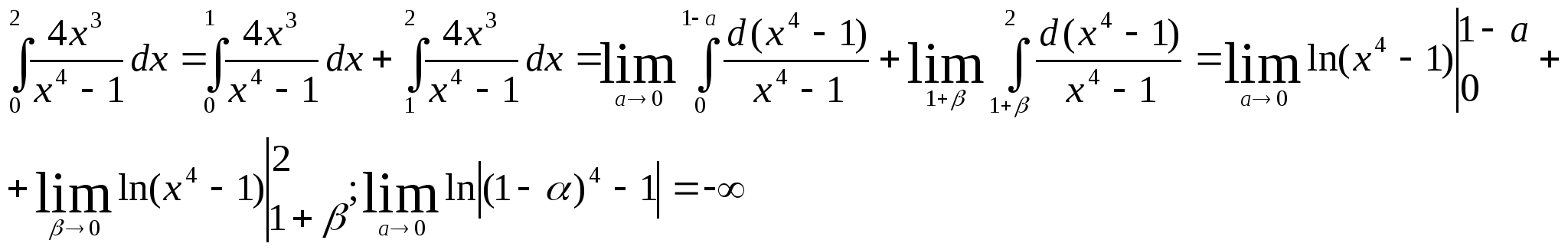
88.Чему равен интеграл 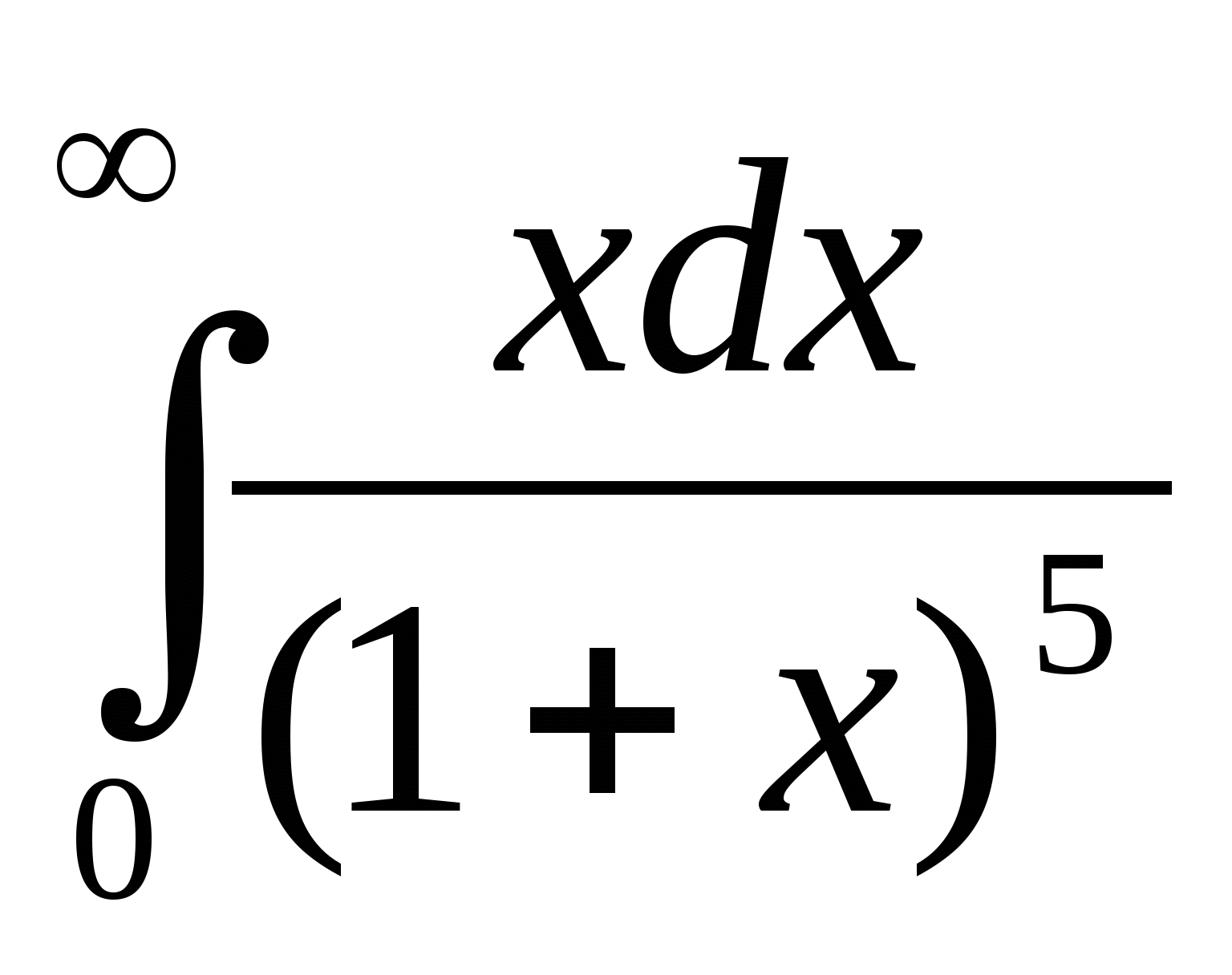 ?
?
a)![]() b)
b) ![]() c)0 d)
c)0 d)![]()
Решение задачи 88.
Интеграл несобственный 1-го рода, функция - правильная рациональная дробь - определена на бесконечном интервале. Разложим дробь на сумму простых дробей, применив искусственный приём.
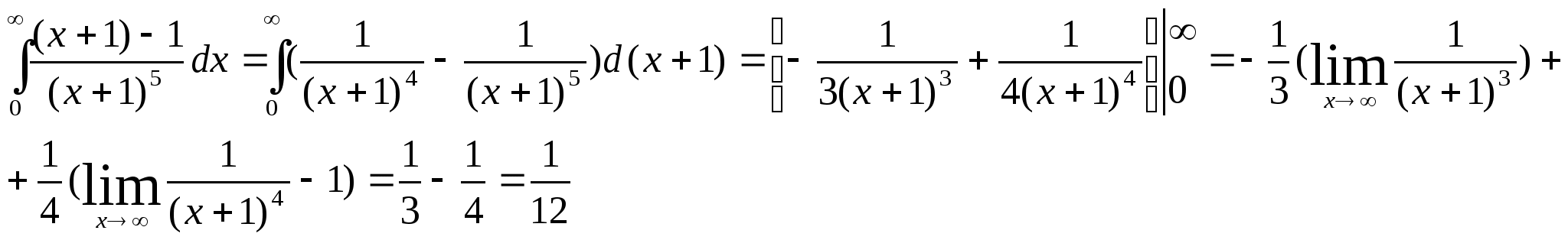
Теория
89.Предел, к которому стремится длина вписанной ломаной линии при условии, что число звеньев неограниченно возрастает и длина наибольшего из них стремится к нулю это:
a) длина дуги
b) длина кривой
с) длина ломанной
d) Нет правильного ответа
90.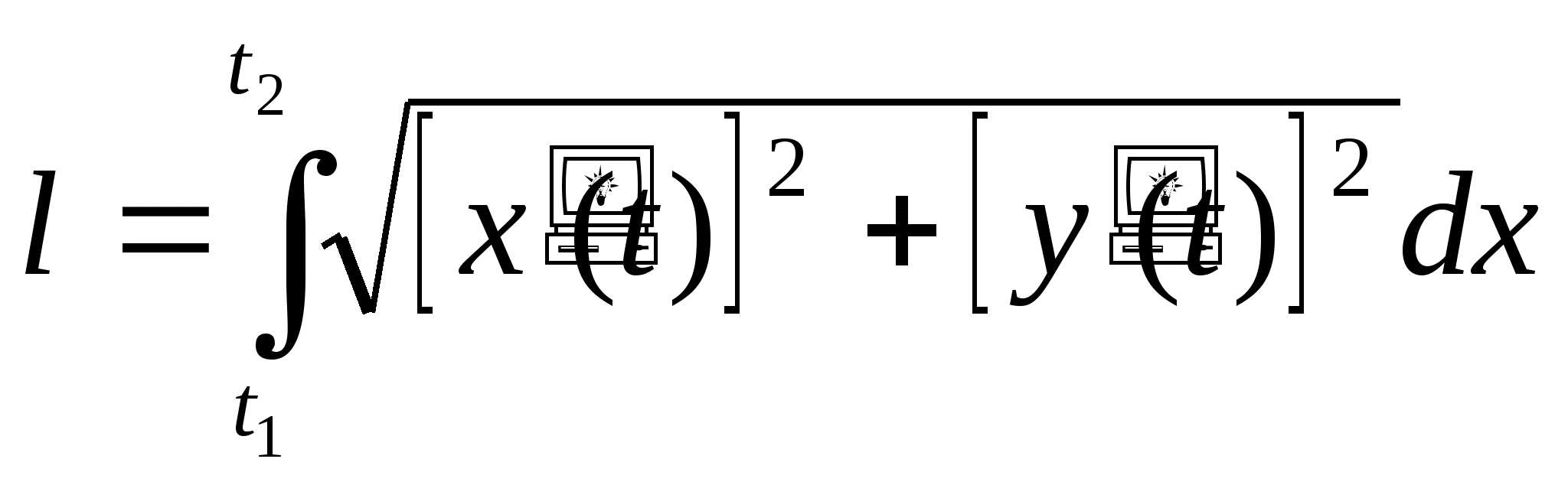 - это формула для вычисления:
- это формула для вычисления:
a) длины дуги, заданной параметрически;
b) длина дуги кривой в полярной системе координат;
с) длина дуги кривой в прямоугольных координатах;
d) длина дуги
91.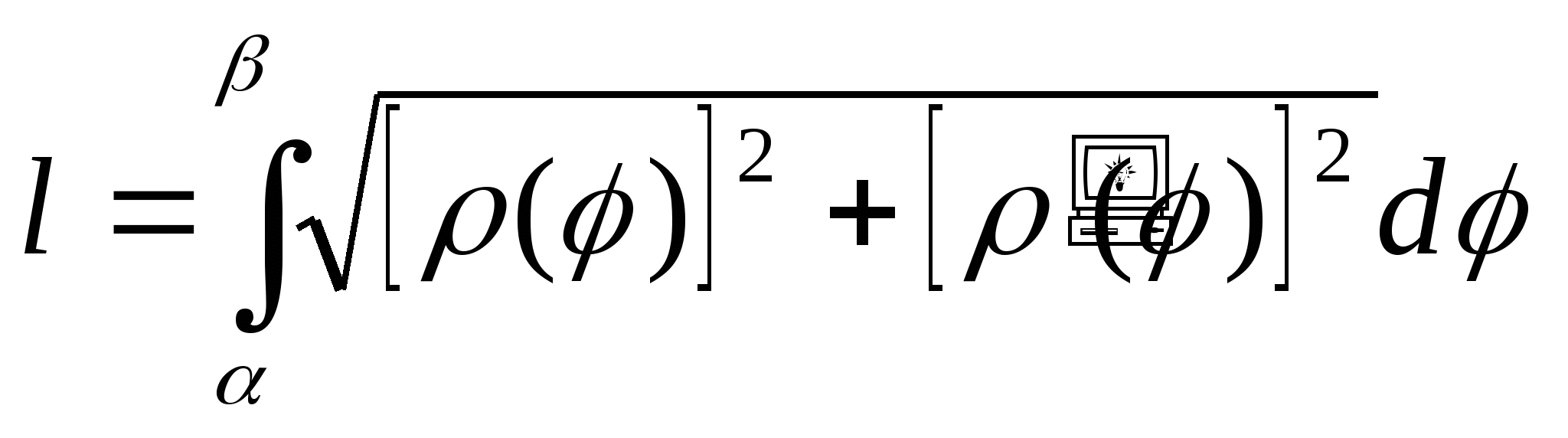 это формула для вычисления:
это формула для вычисления:
a) длины дуги, заданной параметрически;
b) длина дуги кривой в полярной системе координат;
с) длина дуги кривой в прямоугольных координатах;
d) длина дуги
92.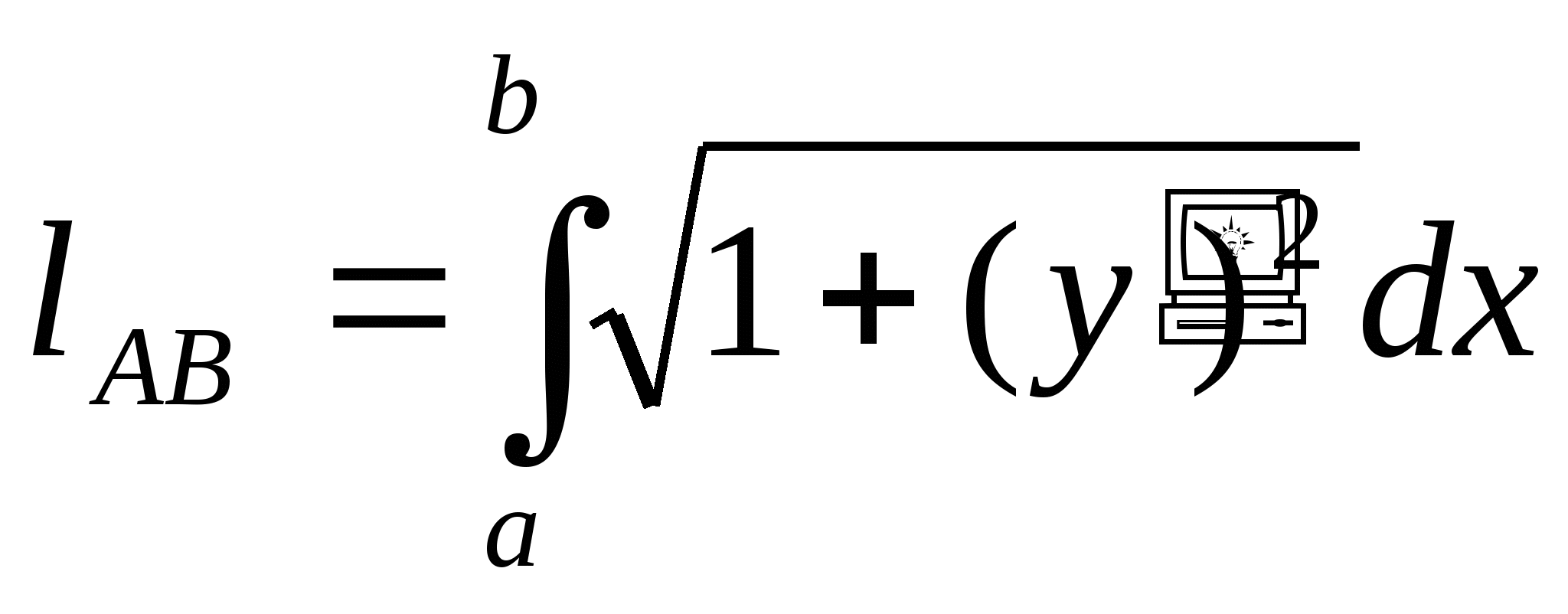
a) длины дуги, заданной параметрически;
b) длина дуги кривой в полярной системе координат;
с) длина дуги кривой в прямоугольных координатах;
d) длина дуги
93.Вставьте в определение недостающее слово:
Несобственным интегралом от функции f(x) в
интервале ![]() называется … интеграла
называется … интеграла 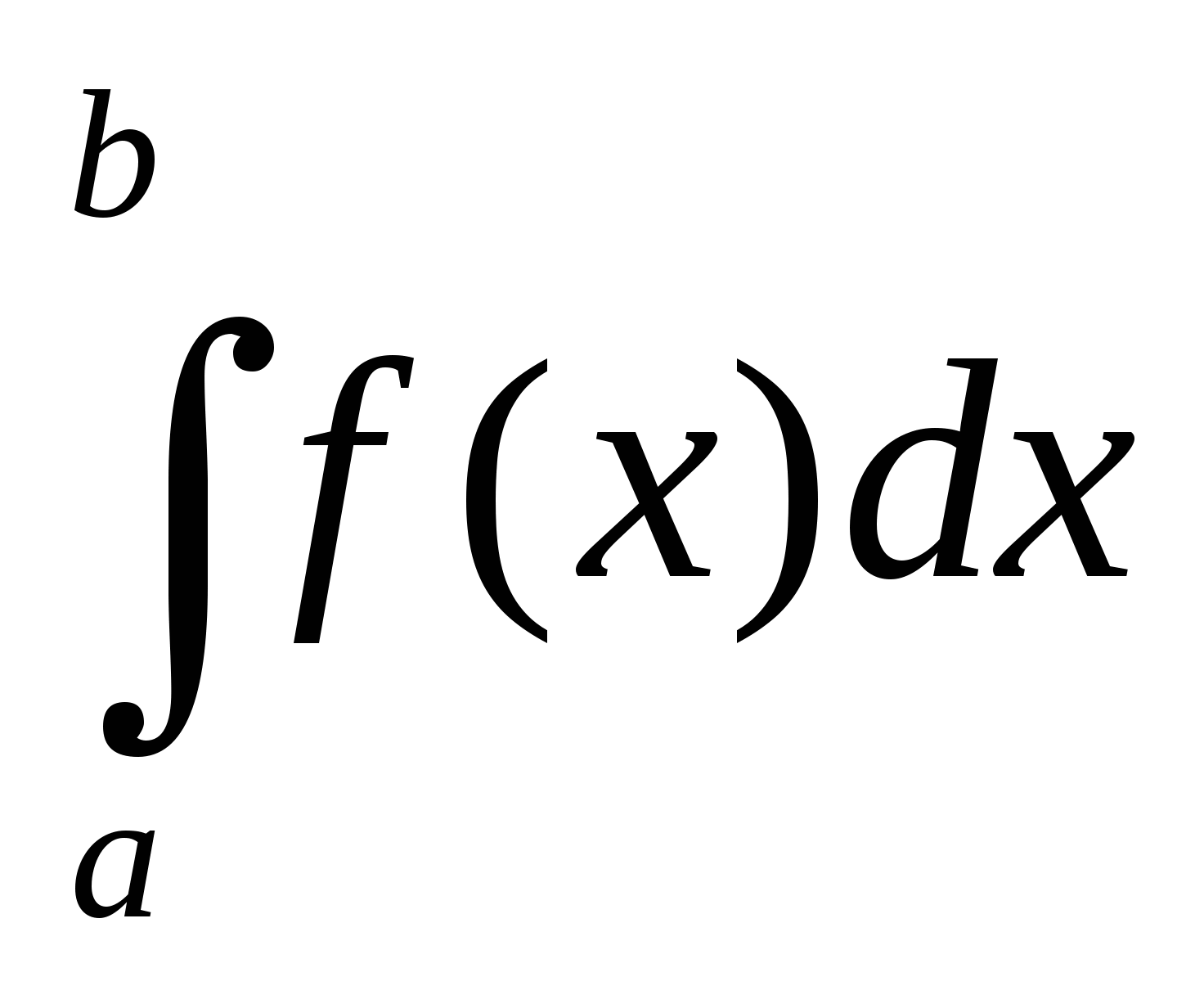 при
при ![]() :
: 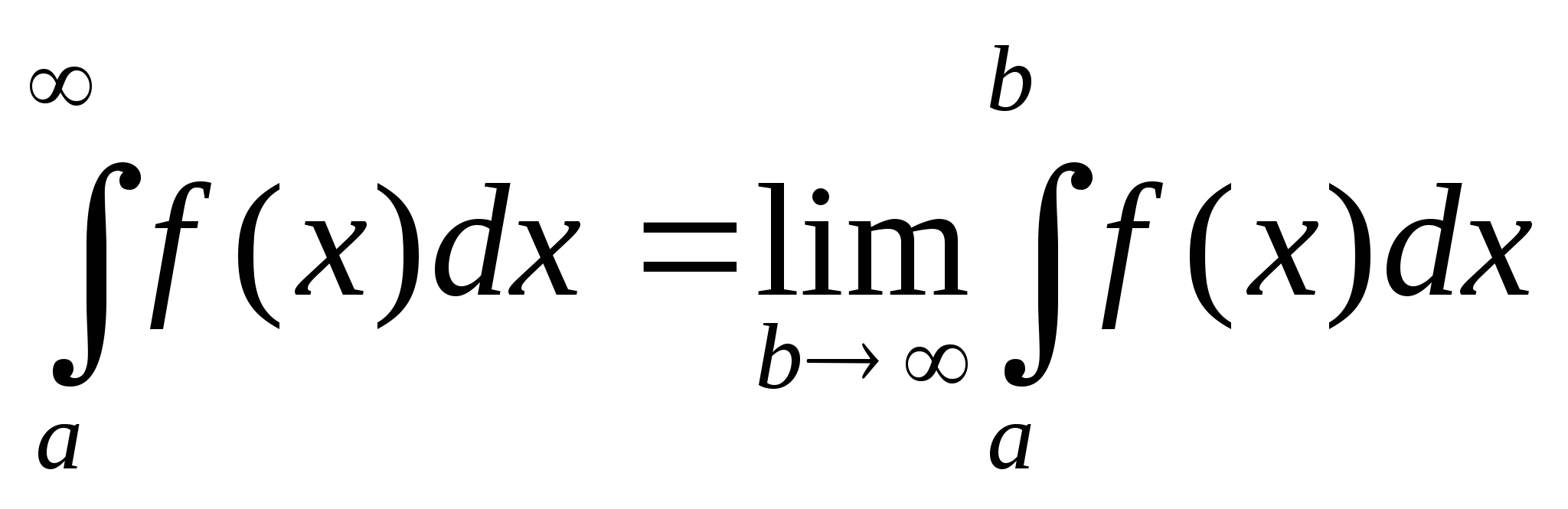 .
.
a)предел
b)интеграл
с)несобственный интеграл
d)собственный интеграл
94.Несобственные интегралы с бесконечными пределами называют несобственными интегралами:
a) II рода
b) I рода
с) III рода
d) нет правильного ответа
95. Какая из ниже перечисленных формул относится к формуле для вычисления площади криволинейной трапеции, ограниченной параметрически заданной кривой?
a)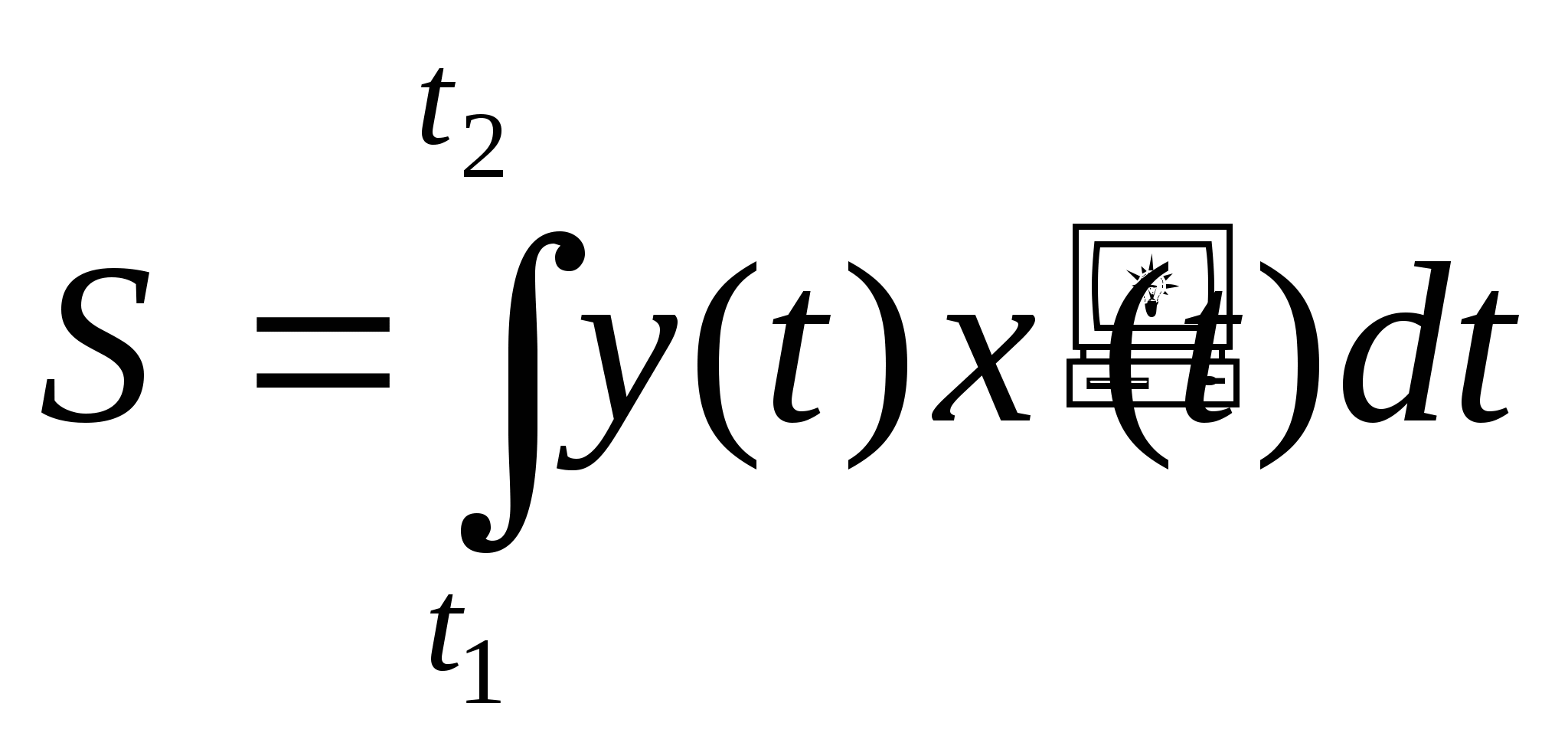
b) 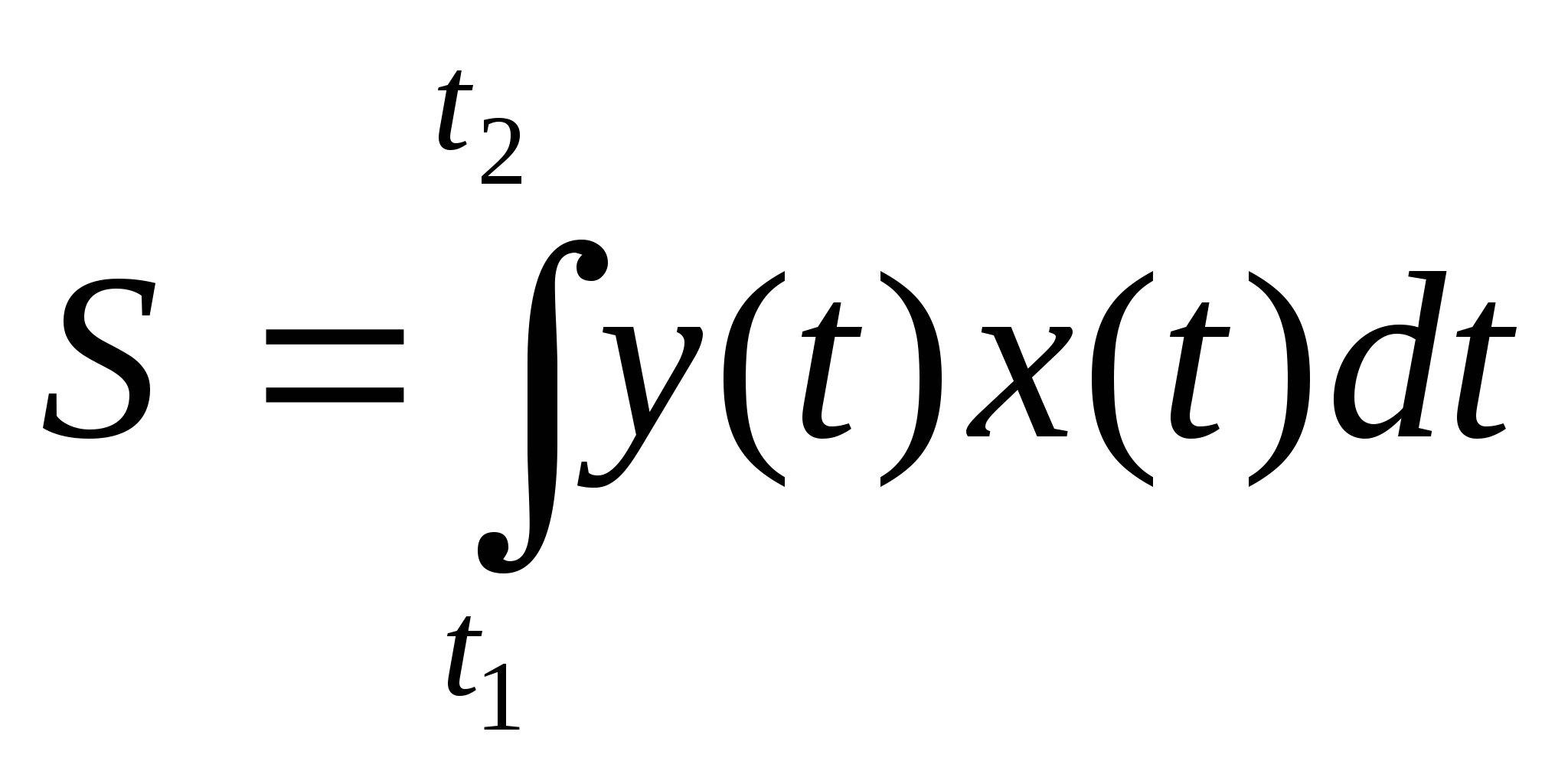
c) 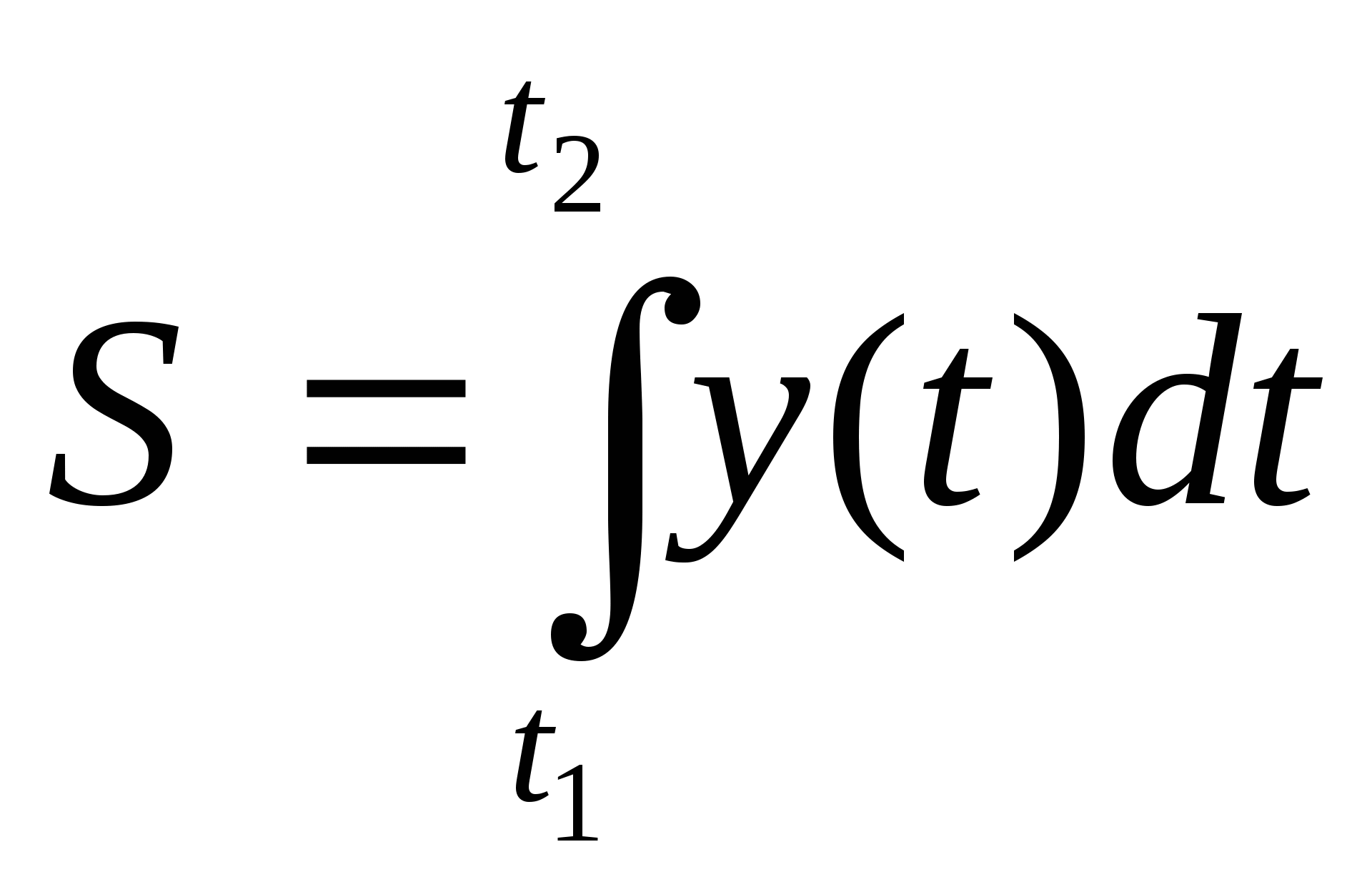
d) ![]()
96.Формула для отыскания площади криволинейного сектора:
a)![]()
b)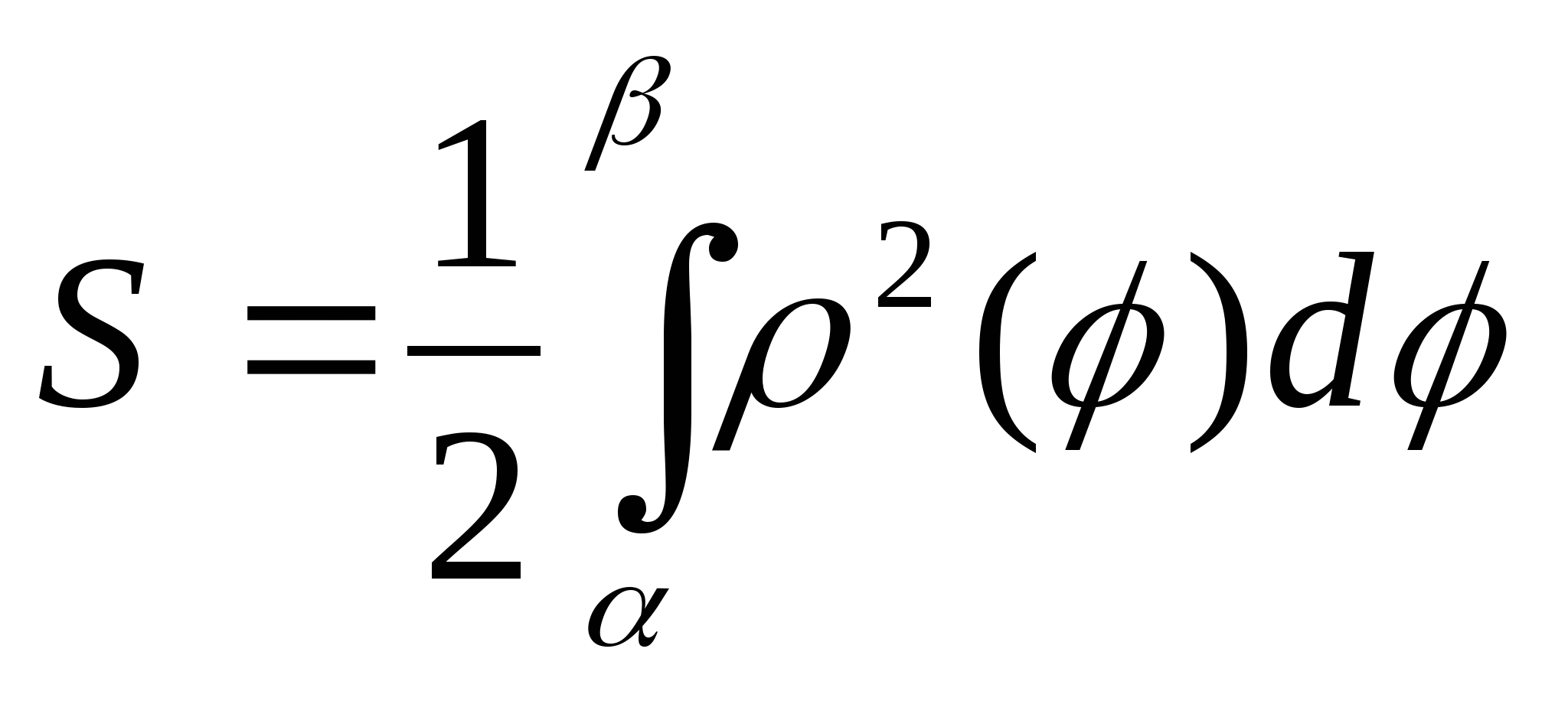
c) 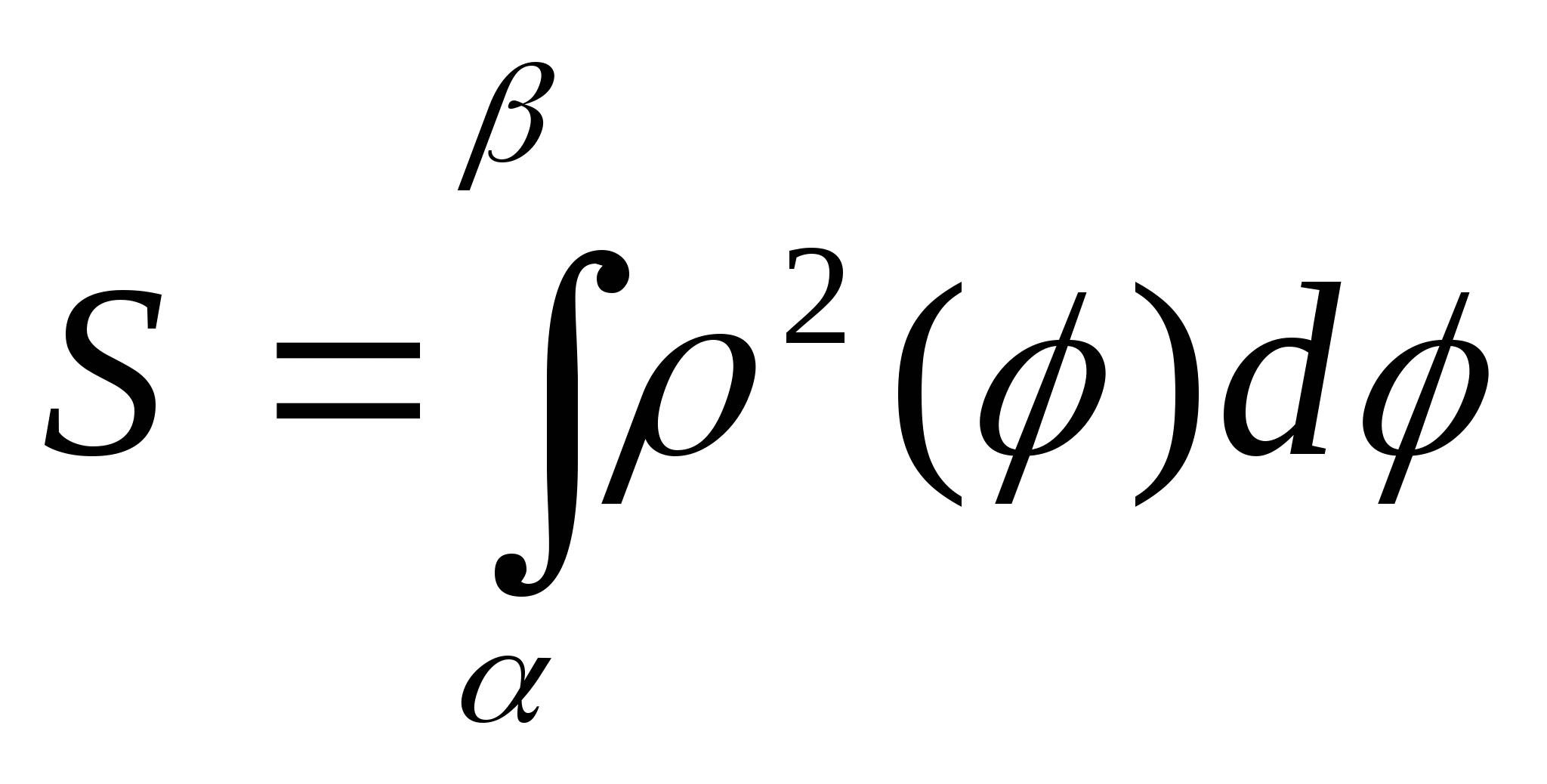
d) ![]()
97.Вставьте недостающее слово:
Криволинейным сектором называется область,
ограниченная лучами ![]()
и линией ![]() , которую любой луч, исходящий из полюса, пересекает не более
чем … .
, которую любой луч, исходящий из полюса, пересекает не более
чем … .
-
в одной точке;
-
в двух точках;
-
в трёх точках
-
в четырёх точках.
98.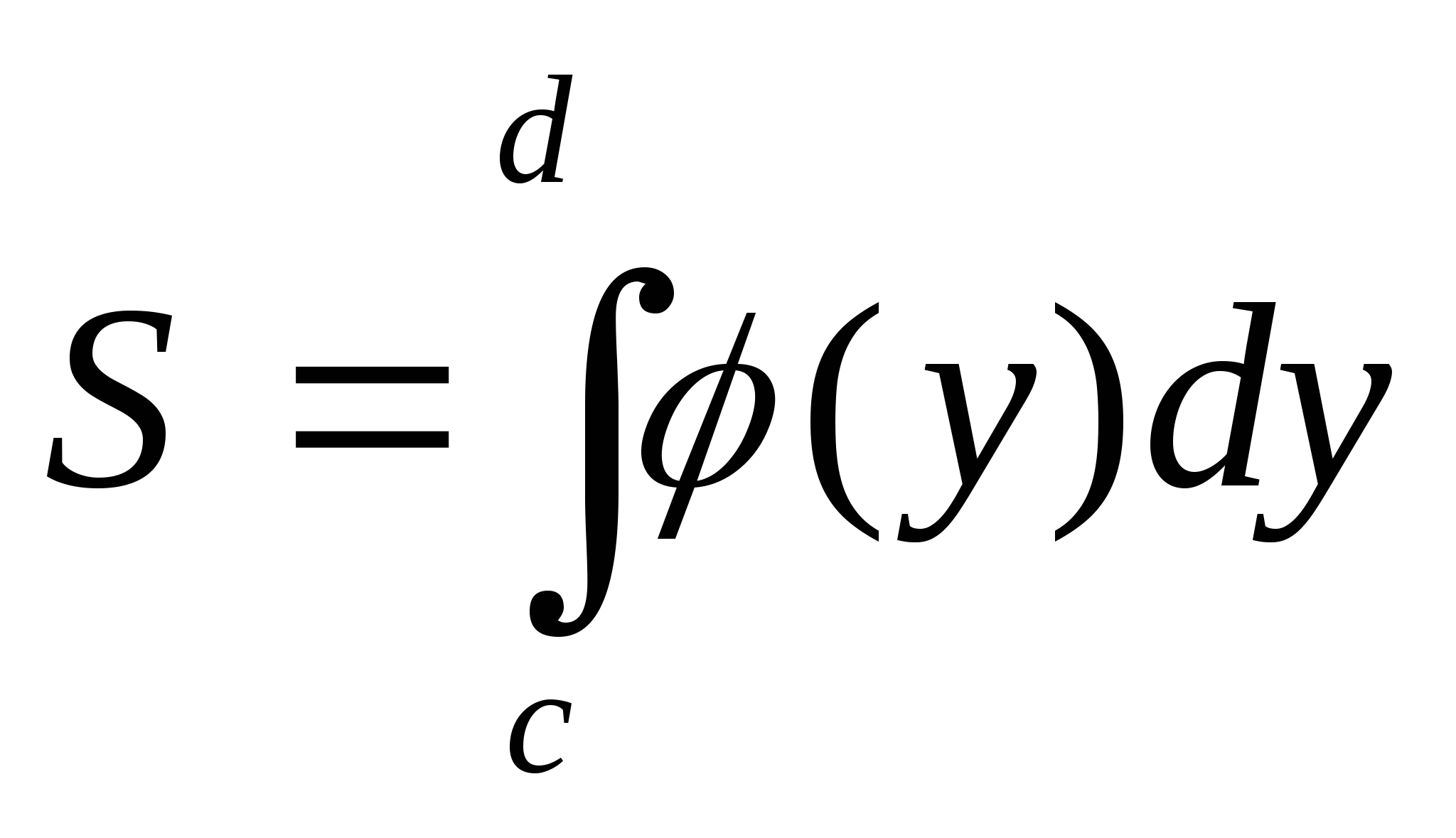 - это формула для вычисления:
- это формула для вычисления:
a) площади фигуры, ограниченной кривыми
![]() и прямыми x=a, x=b;
и прямыми x=a, x=b;
b)площадь трапеции, основанием которой является ось ординат;
с)площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме;
d)площадь криволинейного сектора в полярной системе координат.
99.Какая из ниже перечисленных формул является формулой для определения несобственного интеграла от функции f(x)?
a)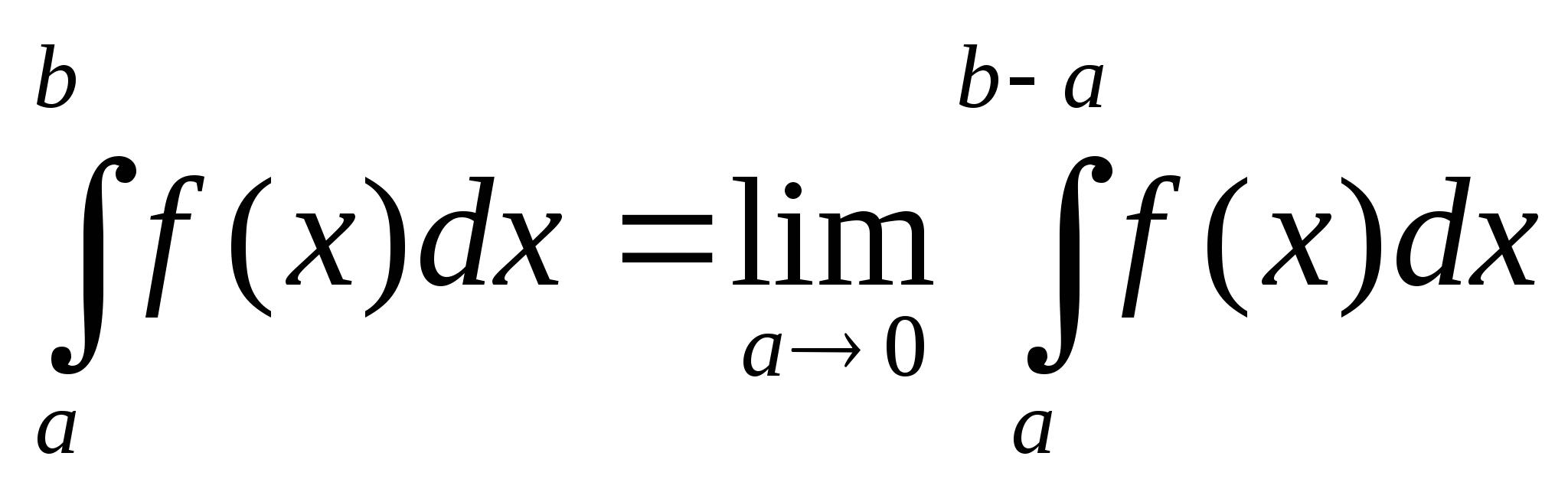
b) 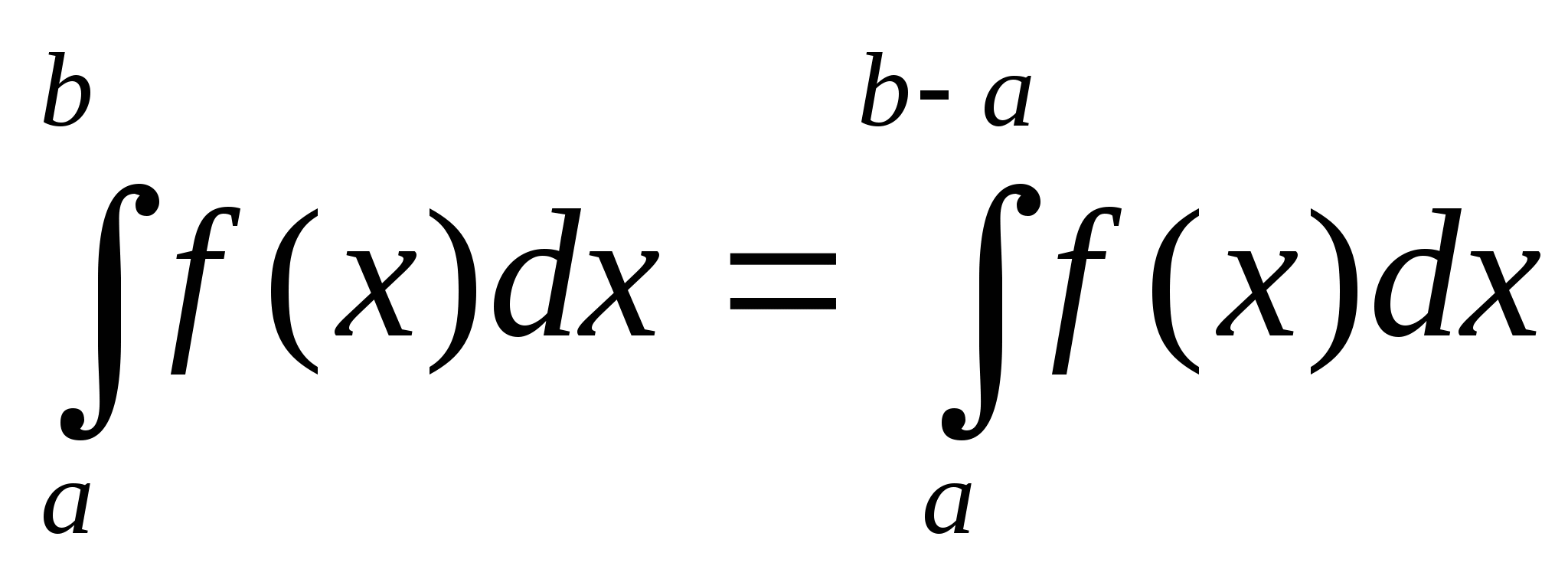
c) 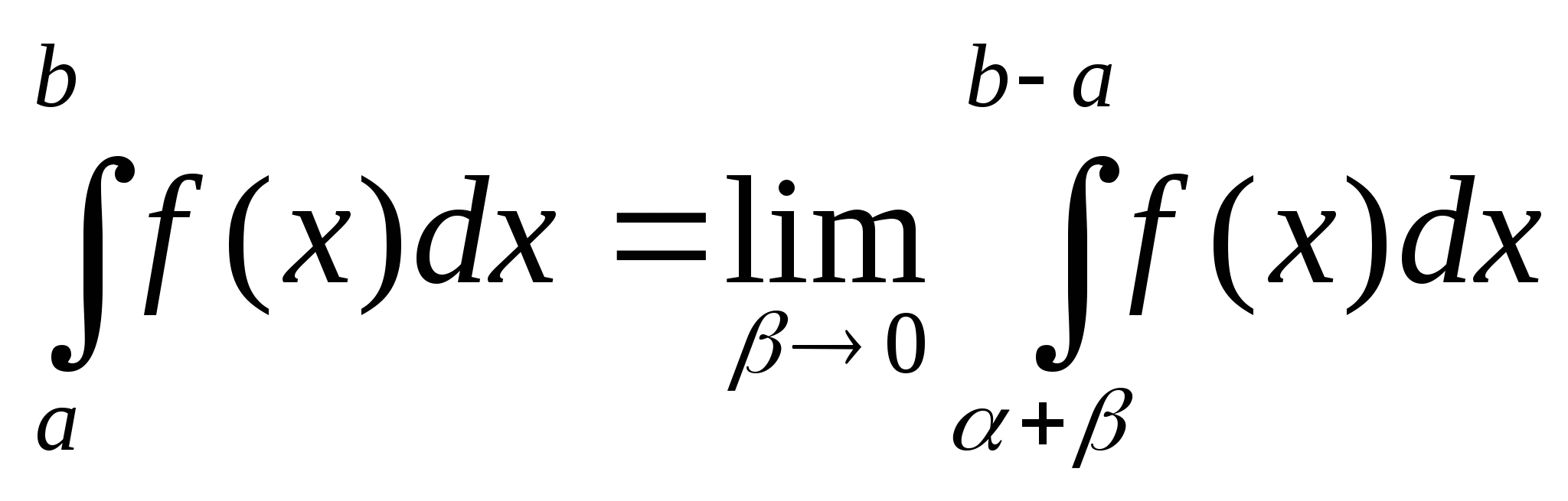
d) 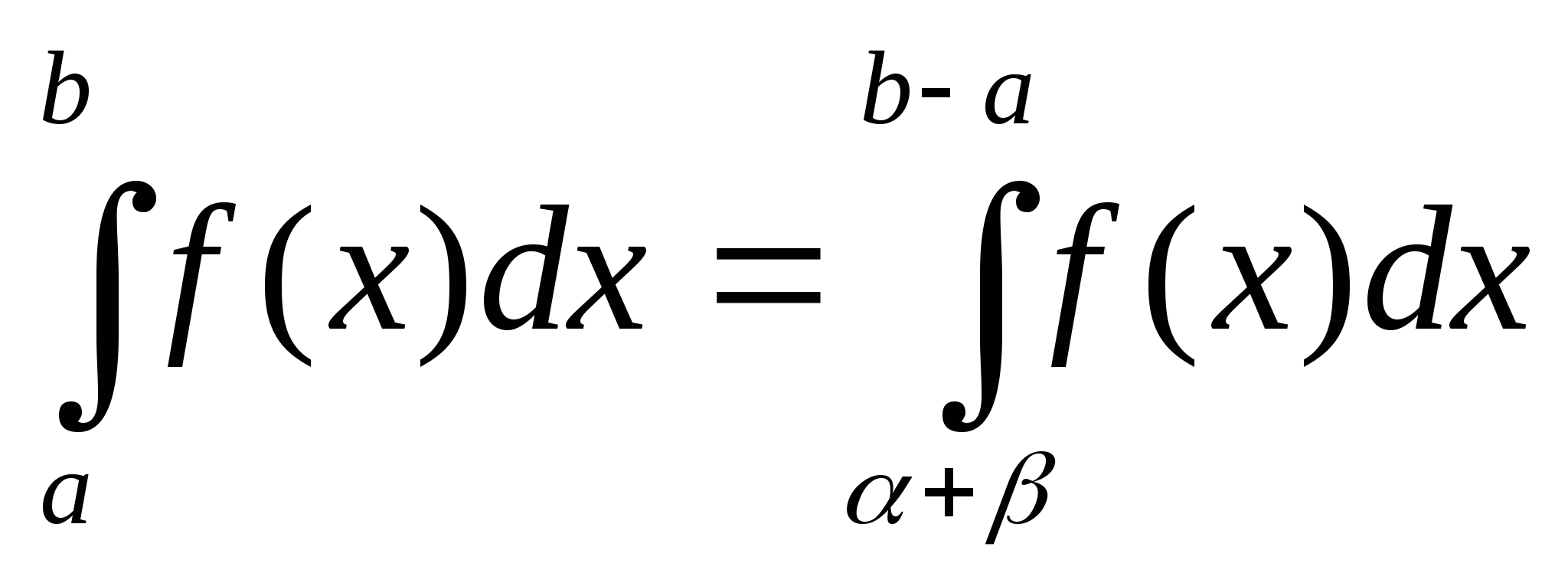
100.Геометрическая интерпретация сходящегося несобственного интеграла 2-го рода это:
a) площадь криволинейной трапеции с бесконечно малой высотой;
b) площадь прямоугольной трапеции;
c) площадь криволинейной трапеции с бесконечно большой высотой;
в) площадь равнобедренной трапеции.
Ключ к тесту
1-a
2-a
3-a
4-a
5-b
6-a
7-a
8-b
9-a
10-c
11-a
12-a
13-c
14-a
15-d
16-c
17-b
18-a
19-d
20-c
21-a
22-a
23-a
24-a
25-a
26-a
27-b
28-b
29-a
30-b
31-c
32-b
33-a
34-b
35-a
36-c
37-a
38-a
39-a
41-a
42-a
43-b
44-b
45-b
46-a
47-a
48-b
49-a
50-a
51-a
52-a
53-a
54-a
55-a
58-a
59-a
60-а
61-a
62-а
63-a
64-a
65-а
66-b
67-a
68-в
69-a
70-a
71-b
72-c
73-b
74-c
75-a
76-b
77-d
78-a
79-a
80-a
81-a
82-a
83-a
84-a
85-b
86-c
87-b
88-a
89-a
90-a
91-c
92-a
93-b
94-b
95-a
96-b
97-a
98-b
99-a
100-c
Список используемой литературы
-
Бугров Я.С. Никольский СМ. Высшая математика: Дифференциальное и интегральное исчисление. М.: Наука, 1984. 432 с.
-
Зорин В.А. Математический анализ: В 2 т. Т. 1. М.: Наука, 1981. 544 с; Т. 2. М.: Наука, 1984. 640 с.
-
Ильин В.А., Позняк Э.Г. Основы математического анализа: В 2 т. Т. 1. М.: Наука, 1982. 616 с; Т. 2. М.: Наука, 1980. 448 с.
-
Кудрявцев Л.Д. Курс математического анализа: В 3 т. М.: Высш. шк., 1988. Т. 1. 712 с; Т. 2. 576 с; Т. 3. 352 с.
-
Уваров В.Б. Математический анализ. М.: Высш. шк., 1984. 288 с.
-
Шилов Г.Е. Математический анализ: Функции одного переменного: В 2 т. Т. 1. М: Наука, 1969. 528с.
91