Применение производной к исследованию функций

Карта - информатор

Тема: Применение производной к исследованию функций.

1. Применение производной к нахождению промежутков возрастания и убывания функции:

Если на промежутке, то функция возрастает на этом промежутке.

Если на промежутке, то функция убывает на этом промежутке.

2. Экстремумы функции:

а) Точки, в которых производная функции равна нулю, называют стационарными.

б) Пусть функция f(x) дифференцируема на интервале (а, в), и

Тогда:

1. если при переходе через стационарную точку 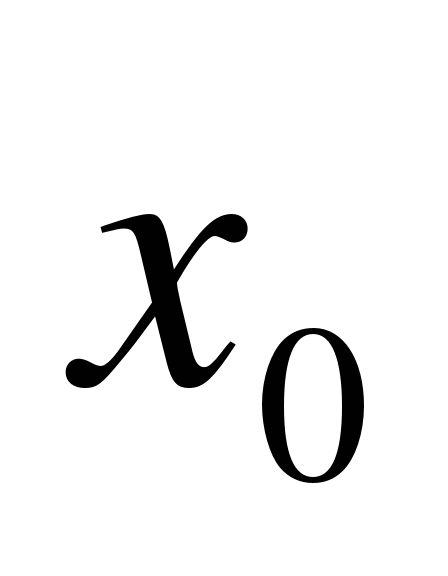функции 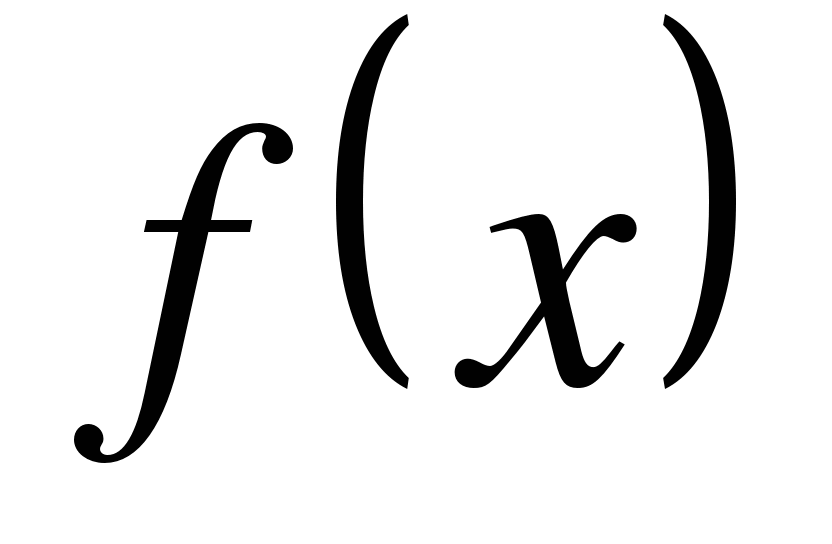ее производная меняет знак с «плюса» на «минус», т.е. справа от точк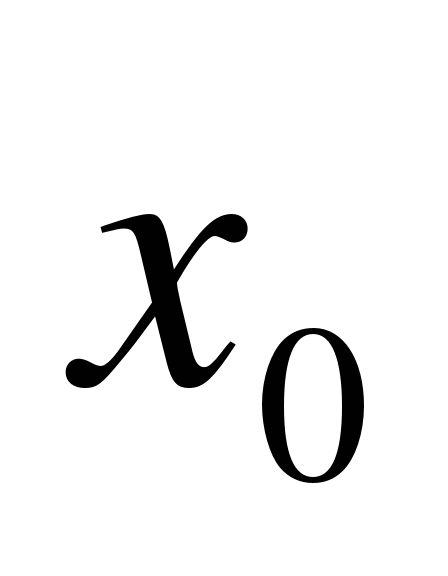и и 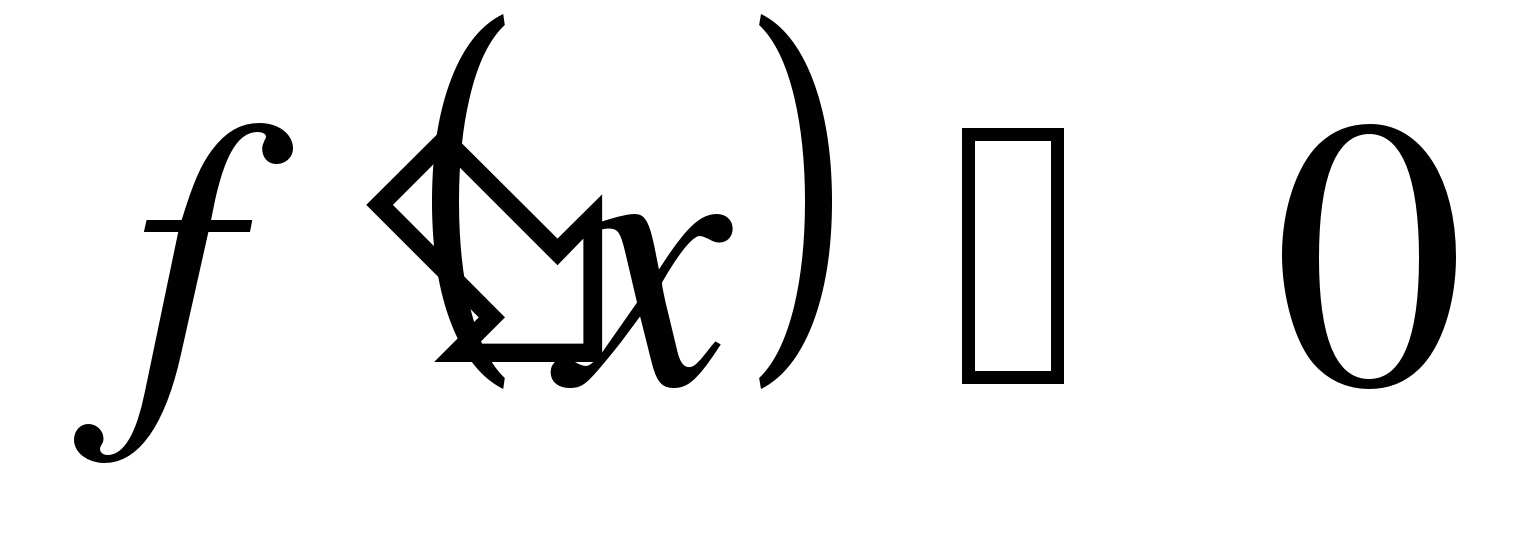слева от точки 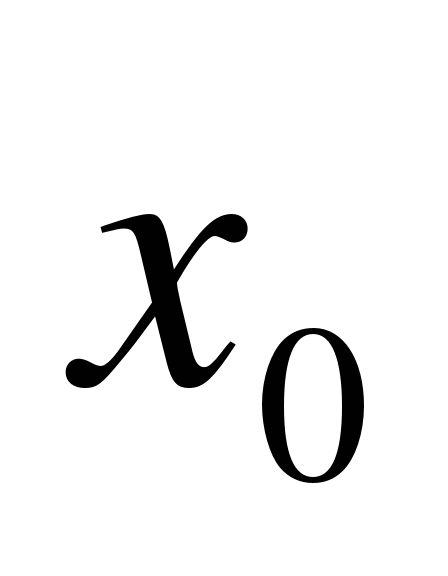, то - точка максимума функции .

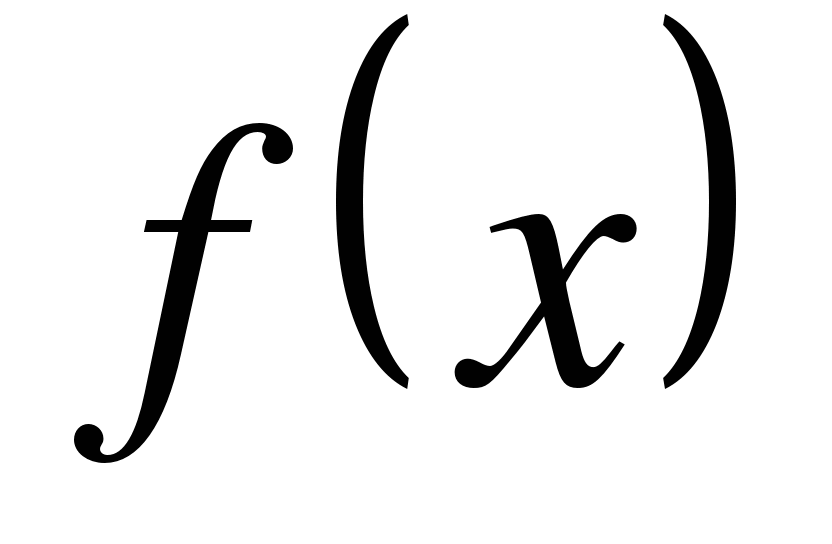2. если при переходе через стационарную точку 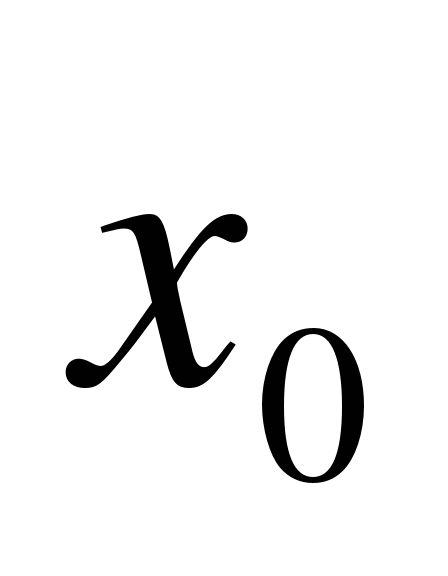функции 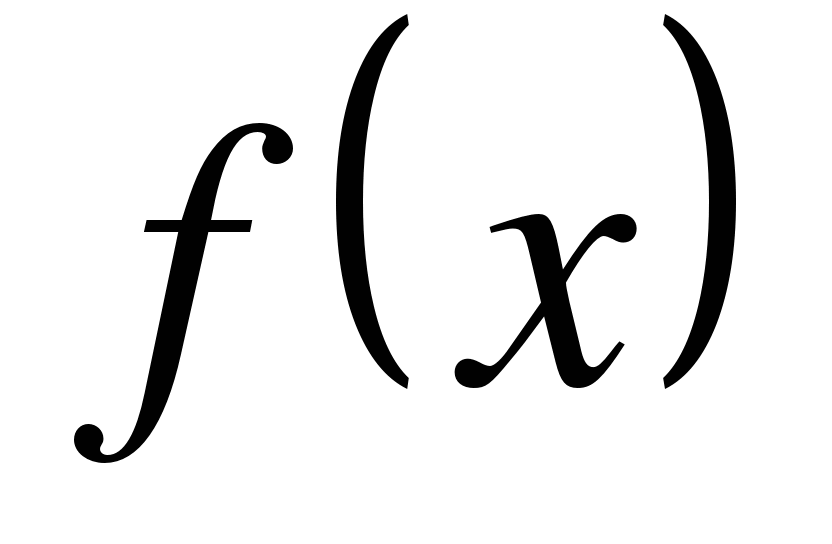ее производная меняет знак с «минуса» на «плюс», то 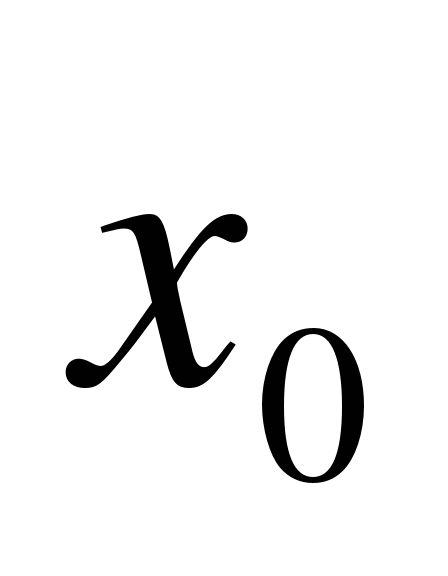- точка минимума функции .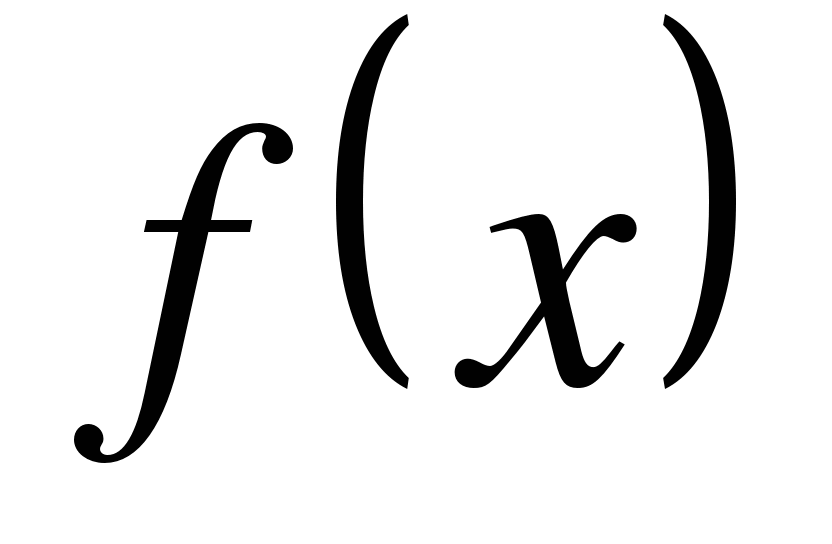

в) Точки минимума и точки максимума называются точками экстремума.

г) Точки, в которых функция имеет производную, равную нулю, или недифференцируема,

называют критическими точками этой функции.

3. Применение производной к построению графиков функций.

План исследования функции:

1. найти область определения функции;

2. найти производную;

3. найти стационарные точки ( решить уравнение );

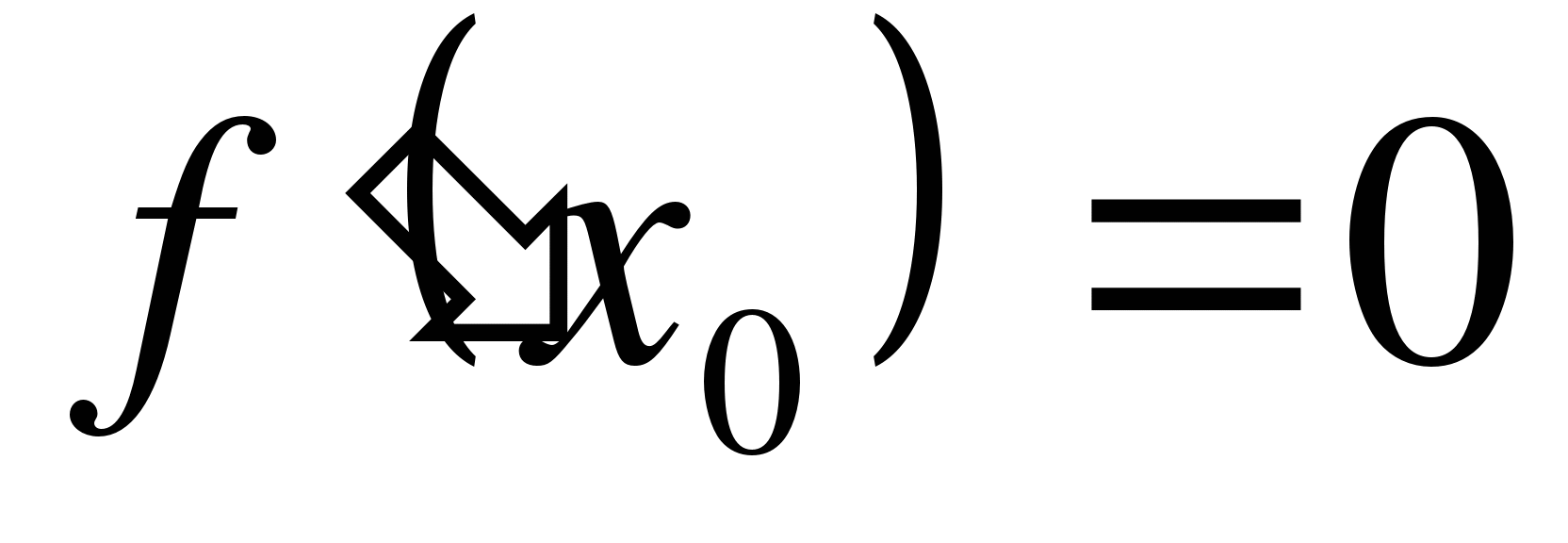4. найти промежутки возрастания и убывания;

5. найти точки экстремума и значения функции в этих точках.

Результаты исследования записать в виде таблицы. Используя таблицу построить график. Для более точного построения найти еще несколько точек графика.

3. Наибольшее и наименьшее значения функции:

Для нахождения наибольшего и наименьшего значений функции на отрезке нужно:

1) найти значения функции на концах отрезка, т.е. числа и .

2) найти ее значения в тех критических точках, которые принадлежат интервалу ;

3) из найденных значений выбрать наибольшее и наименьшее.

Примеры: 1. Найти интервалы возрастания и убывания функции

Решение: решая неравенство находим интервал возрастания, т.е. . Решая неравенство находим интервал убывания, т.е. . Ответ: возрастает на промежутке ; убывает на промежутке ..

2. Найти стационарные точки функции

Решение: Найти производную: Найти стационарные точки, т.е.решить уравнение ; методом интервалов

можно установить, что при при и при

При переходе через точку производная меняет знак с «минуса» на «плюс», точка - точка минимума, при переходе через точку производная не меняет знак, точка не является точкой экстремума.

4.Найти наибольшее и наименьшее значения функции на отрезке

Решение: 1.

2. 3. Стационарные точки: , 4.Интервалу принадлежит одна точка х = 1.

5. Из чисел 0; 2; -2 наибольшее 2, наименьшее -2.