Итоговая контрольная работа по геометрии 10 класс

Вариант 1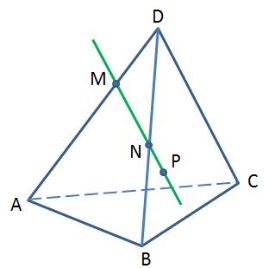

1. Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

2. Точка М не лежащая в плоскости треугольника АВС равноудалена от его вершин, МО - перпендикуляр к плоскости АВС. Точка О является

а) центром вписанной в треугольник АВС окружности;

б) центром описанной возле треугольника АВС окружности;

в) центром тяжести треугольника АВС;

г) точкой пересечения высот треугольника АВС.

3. а Дано: а (АВС),

М АВС - прямоугольный,

С= 90˚

В Доказать: МСВ -

А прямоугольный.

С

4. Через точку А, расположенную по одну сторону от параллельных плоскостей α и β , проведены две прямые, которые пересекают плоскость α в точках В и С, а плоскость β в точках В₁ и С₁ соответственно. Найти длину отрезка ВС, если В₁ С₁ =21 см, АС=3 см, СС₁ =4 см.

5.Из точки к плоскости проведены две наклонные, длины которых относятся как 5:6. Найти расстояние от точки до плоскости, если соответствующие проекции наклонных равны 4 см и см.

6.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

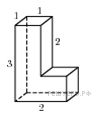
7. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 40, и боковым ребром, равным 55.

8. В правильной треугольной пирамиде боковое ребро равно b, а плоский угол при вершине β. Найти полную поверхность пирамиды.

Вариант 2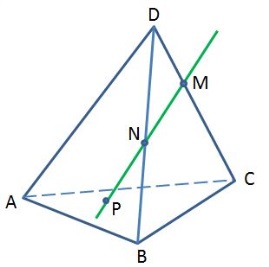

1.Точка Р лежит на прямой МN. Назовите плоскость, которой принадлежит точка Р.

1) АВС 2) DBC 3) DAB 4) DAC

2.Точка М не лежащая в плоскости треугольника АВС равноудалена от его сторон, МО - перпендикуляр к плоскости АВС. Точка О является

а) центром вписанной в треугольник АВС окружности;

б) центром описанной возле треугольника АВС окружности;

в) центром тяжести треугольника АВС;

г) точкой пересечения высот треугольника АВС.

а

3. М Дано: ABCD - ромб,

В С АС ВD = О,

а (АВС).

Доказать: МО ВD.

OOOОО

А D

4.Через точку А, расположенную по одну сторону от параллельных плоскостей α и β , проведены две прямые, которые пересекают плоскость α в точках В и С, а плоскость β в точках В₁ и С₁ соответственно. Найти длину отрезка В₁ С₁, если ВС =10 см, АС=5 см, СС₁ =4 см.

5. Из точки М, взятой вне плоскости, проведены две наклонные, равные 37 см и 13 см. Проекции этих наклонных относятся, как 7:1. Определить расстояние от точки М до плоскости.

6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

7. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 5 и 12, и боковым ребром, равным 17.

8. В основании пирамиды лежит равнобедренный треугольник с углом α при вершине и боковой стороной b. Все боковые ребра наклонены к плоскости основания под углом β. Найти площадь основания и высоту пирамиды.

Вариант 3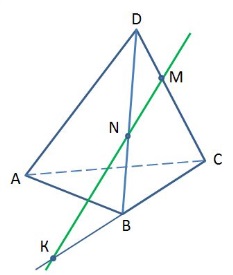

1. Каким плоскостям принадлежит точка К?

1) АВС и ABD 2) ABD и BCD 3) ACD и ABD 4) ABC и BCD

2. Закончите фразу, чтобы получилось верное высказывание:

Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна их линии пересечения, то она …

А) параллельна другой плоскости

Б) пересекается с другой плоскостью

В) перпендикулярна к другой плоскости

Г) не знаю

3. а Дано: ABCD -

М параллелограмм,

В С а (АВС),

МА АD.

Доказать:

А D ABCD - прямоугольник.

4. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А₁, В₁ и М₁. Найдите длину отрезка ММ₁, если отрезок АВ не пересекает плоскость и если: АА₁=3,6 дм, ВВ₁=4,8 дм.

5.Из точки А, удаленной от плоскости на расстояние см, проведены к этой плоскости наклонные АВ и АС под углом 30˚ к плоскости. Их проекции образуют угол 120˚. Найти ВС.

6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

7. Основание прямого параллелепипеда -ромб с острым углом 60˚ и большей диагональю см, меньшая диагональ параллелепипеда образует с плоскостью основания угол 45˚. Найти боковую поверхность параллелепипеда.

8. Основание пирамиды-прямоугольник. Две боковые грани пирамиды содержат ее высоту, которая равна Н, а две другие наклонены к плоскости основания под углами α и β.Найти площадь основания и высоту пирамиды.

Вариант 4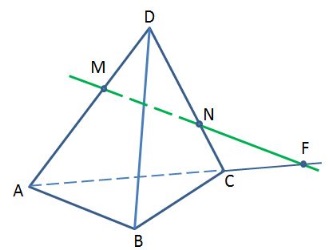

1. Каким плоскостям принадлежит точка F?

1) АВС и ACD 2) ABD и BCD 3) ACD и BCD 4) ABC и BCD

2. На плоскости проведена прямая а и отмечена точка А, не лежащая на этой прямой. Через точку А проведена прямая b, лежащая в этой же плоскости. Каким может быть расположение прямых а и b?

А) они всегда только параллельны Б) они всегда только пересекаются

В) могут быть и параллельными, и пересекающимися Г) не знаю

а Дано: а (АВС),

3. М MD ВС,

В D - середина ВС.

D Доказать: АВ = АС

А

С

4. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В₁ и С₁. Найдите длину отрезка ВВ₁, если СС₁=15 см, АС:ВС=2:3.

5. Из точки к плоскости проведены две наклонные к этой плоскости. Длина одной из них равна см, а длина ее проекции 8 см. Угол между проекциями наклонных равен 60˚, а длина отрезка, что соединяет основания наклонных, равна 7 см. Найти длину второй наклонной.

6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).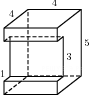

7. В прямом параллелепипеде стороны основания равны см и 5см.Они образуют угол в 45˚, меньшая диагональ параллелепипеда равна 7 см. Определить его полную поверхность.

8. В основании пирамиды лежит прямоугольный треугольник с катетом а и прилежащим острым углом β. Найти площадь основания и высоту пирамиды, если все боковые ребра наклонены к ее основанию под углом α.

Вариант 5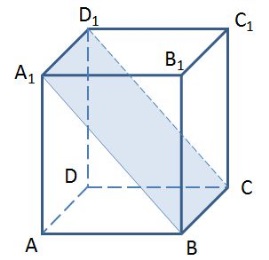

1. Назовите прямую, по которой пересекаются плоскости A₁BC и A₁AD.

1) DC 2) A₁D₁

3) D₁D 4) D₁C

2. Даны две прямые, пересекающиеся в точке С. Лежит ли с ними вместе в одной плоскости любая третья прямая, имеющая с каждой из данных прямых общую точку?

А) всегда да Б) всегда нет В) лежит, но не всегда Г) не знаю

3. а Дано: ABCD -

М прямоугольник,

В С а (АВС),

Доказать: МА АD.

А D

4. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В₁ и С₁. Найдите длину отрезка ВВ₁, если СС₁=8,1 см, АВ:АС=11:9.

5. Из точки, удаленной на расстоянии 4 см от плоскости, проведены две наклонные к этой плоскости длиной 5 см и см. Угол между проекциями этих наклонных равен 60˚. Найти расстояние между основаниями наклонных.

6.

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

7.Стороны основания прямоугольного параллелепипеда равны 5 см и 6 см, а его диагональ см. Найти площадь полной поверхности параллелепипеда.

8. Основанием пирамиды служит прямоугольный треугольник с острым углом α и гипотенузой с. Каждая боковая грань наклонена к основанию под углом β. Найти боковую поверхность пирамиды.

Вариант 6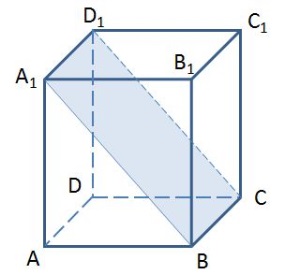

1.Назовите прямую, по которой пересекаются плоскости DCC₁ и A₁BC.

1) DC 2) A₁D₁

3) D₁D 4) D₁C

2.Закончите фразу, чтобы получилось верное высказывание:

Если прямая пересекает одну из двух пересекающихся прямых, то она …

А) лежит в этой же плоскости В) перпендикулярна ко второй прямой

Б) пересекает и вторую прямую Г) не знаю

3. а Дано: а (АВС),

М МВС - прямоугольный,

МСВ= 90˚

В Доказать: АСВ -

А прямоугольный.

С

4. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А₁, В₁ и М₁. Найдите длину отрезка ММ₁, если отрезок АВ не пересекает плоскость и если: АА₁=8,3 см, ВВ₁=4,1 см.

5. Из точки к плоскости проведены две наклонные, которые равны по см каждая. Угол между наклонными 60˚, а угол между их проекциями-прямой. Найти расстояние от этой точки до плоскости.

6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

7. Найти площадь полной поверхности прямой призмы, в основании которой лежит равнобедренный треугольник с основанием 8 см и проведенной к ней высотой, равной 3см, если высота призмы равна 6 см.

8. Основанием пирамиды служит прямоугольный треугольник с острым углом α. Высота пирамиды Н. Каждое боковое ребро составляет с ее основанием угол β. Найти площадь основания.

Вариант 7

1.Выберите верные высказывания:

1) Любые четыре точки лежат в одной плоскости.

2) Через прямую и не лежащую на ней точку проходит только одна плоскость.

3) Если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости .

4) Две плоскости могут иметь только одну общую точку.

2. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Можно ли утверждать, что прямые а, b и с лежат в одной плоскости?

А) да Б) нет В) не всегда Г) не знаю

а

3. М Дано: ABCD - ромб,

В С АС ВD = О,

а (АВС).

Доказать: МО AC.

OOOОО

А

D

4. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А₁, а сторону ВС в точке В₁. Найдите длину отрезка А ₁В _1,если АВ = 8 см, АА₁ : А₁С = 5 : 3.

5. Из точки к плоскости проведены две наклонные, длины проекций которых на плоскость равны по 3 см каждая. Угол между наклонными 60˚, а угол между их проекциями-прямой. Найти расстояние от этой точки до плоскости.

6. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

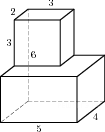
7. В основании прямой призмы лежит прямоугольный треугольник, гипотенуза которого равна 10 см, а один из катетов-6 см. Найти площадь полной поверхности призмы, если ее высота равна 8 см.

8. В правильной треугольной пирамиде боковое ребро равно b и образует с высотой пирамиды угол α. Найти площадь основания и высоту пирамиды.