- Учителю
- Конспект урока по математике на тему 'Решение линейных неравенств с одной переменной' (6 класс)
Конспект урока по математике на тему 'Решение линейных неравенств с одной переменной' (6 класс)
























 Тема урока: Решение линейных неравенств с одной переменной.
Тема урока: Решение линейных неравенств с одной переменной.
Цель урока: освоение обучающимися базисных основ математики, формирование у них высокой культуры межличностного общения.
Задачи урока: 1) организовать урок таким образом, чтобы учащиеся смогли оценить собственный уровень освоенности данной темы, увидеть свои достижения и расширить знания в ходе совместной работы в группах;
2) выявить недочеты для дальнейшего их устранения;
3) оценить знания каждого учащегося по данной теме.
Тип урока: урок-путешествие
Ход урока:
Этапы
Деятельность учителя
Деятельность учащихся
1.
Здравствуйте, садитесь. Подпишите информационные листы, запишите число и тему урока «Решение линейных неравенств с одной переменной». Сформулируйте и запишите, какую цель вы ставите для себя на этом уроке.
На партах лежать листы
Цель, которую я ставлю перед собой:
- узнать …
- расширить свои знания…
- применить…
- связать…
- вспомнить…
- задать вопрос…
- найти…
- установить …
- оспорить …
- структурировать …
- выяснить …
- оценить …
Приветствуют учителя, садятся за парты. Подписывают информационные листы, записывают число и тему урока.
Формулируют и записывают цель урока.
Несколько человек озвучивают свою цель урока.
2.
Прежде чем научиться решать неравенства, вы научились решать уравнения путём их преобразования. Решите уравнение и узнаете, чему будет посвящен наш урок.
В группе нужно решить уравнение и на доске расположить букву соответственно получившемуся ответу.
Уравнения:
О)  ;
;
Л)  ;
;
И)  ;
;
М)  ;
;
П)  ;
;
А)  ;
;
Д) 39.
39.
15,5
-90
-2
2
70
-2
-50
-2,5
-50
О
Л
И
М
П
И
А
Д
А
Решают уравнения в группах, записывают решение каждый на информационном листе.
Составляют на доске слово «Олимпиада»
3.
Мы отправляемся в путешествие по объектам зимней олимпиады. Старт нашему путешествию положен и вы можете занести первый результат в таблицу личных достижений. За правильно решенное уравнение 5 б.
Выполнив второе задание, вы повторите числовые промежутки и узнаете, куда же отправиться наша делегация.
Установите соответствие:







 Г
Г
 В
В
 Д
Д
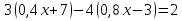 Р
Р
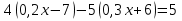 А
А
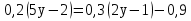 Б
Б
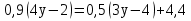 С
С
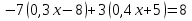 Й
Й
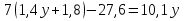 К
К
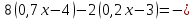 О
О
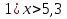 Е
Е
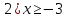 Ш
Ш
Взаимопроверка в парах.
1-5; 2-8; 3-7; 4-6; 5-11; 6-4; 7-1
Мы находимся во дворце зимнего спорта «Айсберг». Здесь начались самые первые соревнования по командному фигурному катанию за 2 дня до открытия олимпиады. Архитектурные очертания объекта соответствуют его названию.
Прежде чем приступить к решению неравенств, давайте вспомним алгоритм решения линейных неравенств с одной переменной.
Ледовая арена «Шайба» - своеобразный символ хоккея. По характерному кличу «Шайбу!» в любой точке мира, где проходят соревнования по хоккею можно узнать русских болельщиков. Поэтому такое название Ледовой Арены делает ещё один акцент на том, что Олимпийские игры принимает Россия.
А вам необходимо в группах собрать домино и разгадать шифрограмму.
Домино:
Старт
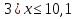
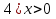
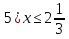
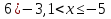
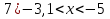
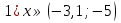
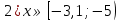
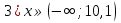
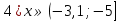
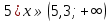
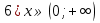
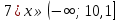
Финиш
Наше домино закончилось числом 17. А чем этот номер примечателен для хоккея? Кто играл под этим номером?
Сейчас мы с вами посетим горнолыжный центр «Роза-Хутор», где нас ждёт скоростной спуск, но не по одному, а целой командой.
Испорченный телефон:
Команда, получившая верный ответ получает 1 б, а команда, которая быстрей всех справиться с этим заданием получает дополнительный 1 б.
Когда участник вашей команды будет записывать ответ у доски, команда должна изобразить езду на лыжах.
Заносят результат в таблицу
(максимум 5 б)
Устанавливают соответствие между неравенством и числовым промежутком.
Собирают слово «Айсберг»
Проверяют работу соседа по парте, заносят результат в таблицу (максимум 7 баллов)
5 человек выходят к доске, собирают алгоритм.
Собирают слово «Шайба»
В группах собирают домино и разгадывают шифр, проверяет другая группа.
Заносят результат в таблицу (максимум 6 баллов)
Играют в испорченный телефон, зарабатывают дополнительные баллы (максимум 2 балла)
4.
А мы отправляемся на «Русские горки» - это комплекс для прыжков с трамплина. Здесь трамплины различной высоты и различной сложности. Каждый из вас будет участвовать в индивидуальном зачете. Вам предстоит решить в течение 5 минут неравенства различной сложности. Это и будет своего рода трамплином, который вам нужно преодолеть. Высоту трамплина каждый выбирает сам. Кроме того у нас будут назначены консультанты, к которым вы сможете обратиться 1 раз.
I вариант
1) 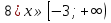 ;
;
2) 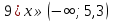 ;
;
3) 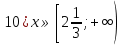 .
.
II вариант
1) 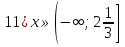 ;
;
2) 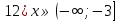 ;
;
3) 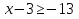 .
.
Давайте проверим результат.
На этом наше путешествие закончилось. Надо подвести итог и оценить свою работу.
28-30 б - «5»
23-27 б - «4»
18-22 б - «3»
меньше 18 - «штрафной круг»
Решают неравенства.
Проверяют работу одноклассника, заносят баллы в таблицу (максимум 10 б)
Подсчитывают баллы, выставляют оценки.
5.
Откройте дневники, запишите домашнее задание. Решить задачу:
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
Записывают домашнее задание
6.
Перед вами пьедестал почёта. Как вы считаете, какого места вы сегодня достойны и на какой ступеньке находитесь вы?
Итак, в копилку Казахстана добавились … и в общем зачете мы выходим на первое место!!!
А кто сегодня был успешнее всех, кто добился высоких результатов? В чем секрет вашего успеха?
Урок закончен. До свидания!
Располагаются на пьедестале
Прощаются с учителем.
Информационный лист ____________________________________________
Тема урока: _______________________________________________________
________________________________________________________
Цель урока: _______________________________________________________
Таблица личных достижений
-
№
Задание
Максимальное
кол-во баллов
Набранное кол-во баллов
1
Старт
5 б
2
Дворец зимнего спорта
7 б
3
Ледовая арена
6 б
4
Скоростной спуск
2 б
5
Русские горки
10 б
Финиш
Результат
1. Решите уравнение ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
2. Установите соответствие







 Г
Г
 В
В
 Д
Д
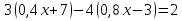 Р
Р
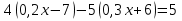 А
А
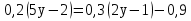 Б
Б
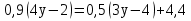 С
С
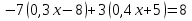 Й
Й
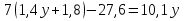 К
К
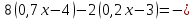 О
О
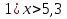 Е
Е
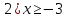 Ш
Ш
1) -
2) -
3) -
4) -
5) -
6) -
7) -
3. Решите неравенство
I вариант
1) 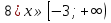 ;
;
2) 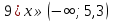 ;
;
3) 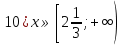 .
.
II вариант
1) 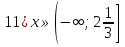 ;
;
2) 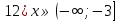 ;
;
3) 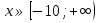 .
.
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Приложения к уроку
О
Л
И
М
П
И
А
Д
А
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В обеих частях неравенства выполнить тождественные преобразования
Ш
Перенести слагаемые, содержащие неизвестную, в левую часть, а свободные члены в правую
А
Привести
подобные
слагаемые
Й
Разделить обе части неравенства на коэффициент при неизвестном
Б
Найти решение неравенства и записать его в виде числового промежутка
А
Старт
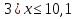
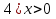
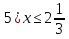
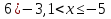
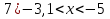
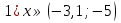
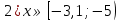
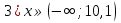
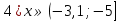
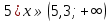
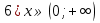
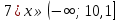
Финиш
Старт
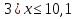
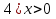
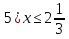
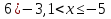
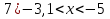
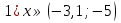
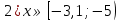
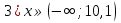
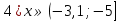
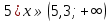
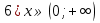
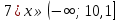
Финиш
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков. |
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|
| Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
| Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков. |
|
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков. |
Биатлонист выстрелил в мишень 10 раз. Если за каждое точное попадание он получит 5 очков, то при каждом промахе он теряет 3 очка. Оцените, сколько точных попаданий в мишень должен сделать биатлонист, чтобы в конце гонки получить больше 34 очков.
|