Переводная аттестация по математике в форме ОГЭ в 8 классе.

</ ПЕРЕВОДНАЯ АТТЕСТАЦИОННАЯ РАБОТА ПО МАТЕМАТИКЕ

В ФОРМЕ ОГЭ 8 КЛАСС

Составитель: Щёголева Л. Ф. , учитель высшей категории.

ВАРИАНТ 1.

Задание 2 № 205776.) Какое из чисел отмечено на координатной прямой точкой A?

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

Задание 3 № 137272.) Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 2) 3) 4) 4

Задание 4 № 137381.) Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

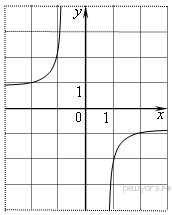
Задание 5 № 193092.) Найдите значение по графику функции , изображенному на рисунке.1)

2)

3)

4)

Задание 7 № 140.) Упростите выражение , найдите его значение при ; . В ответ запишите полученное число.

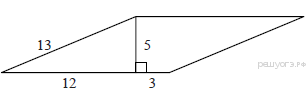
Задание 11 № 91. ) Найдите площадь параллелограмма, изображённого на рисунке.

Задание 12 № 323618.) Найдите тангенс угла AOB, изображённого на рисунке.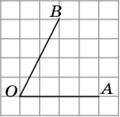

Задание 13 № 197.) Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Задание 17 № 322903.) Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?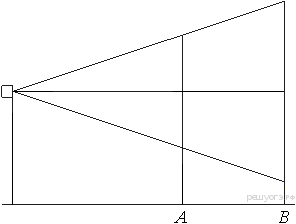

Задание 20 № 311543.) Площадь любого выпуклого четырехугольника можно вычислять по формуле , где - длины его диагоналей, а угол между ними. Вычислите , если .

ВАРИАНТ 2.

Задание 2 № 314146. Одна из точек, отмеченных на координатной прямой, соответствует числу

Какая это точка? В ответе укажите номер правильного варианта.

1) точка A 2) точка B 3) точка C 4) точка D

Задание 3 № 137281. Вычислите:

В ответе укажите номер правильного варианта.

1) 2) 3) 4)

Задание 4 № 137382. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

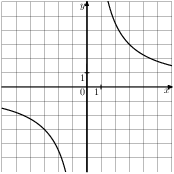
Задание 5 № 203719. Найдите значение по графику функции , изображенному на рисунке.

Задание 7 № 311329. Упростите выражение и найдите его значение при . В ответ запишите полученное число.

Задание 11 № 117. Найдите площадь трапеции, изображённой на рисунке.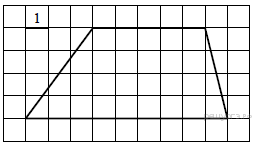

Задание 12 № 314836. Найдите тангенс угла В треугольника ABC, изображённого на рисунке.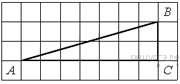

Задание 13 № 169926. Какие из следующих утверждений верны?

1) Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник.

2) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм - ромб.

3) Если один из углов, прилежащих к стороне параллелограмма, равен 50°, то другой угол, прилежащий к той же стороне, равен 50°.

4) Если сумма трех углов выпуклого четырехугольника равна 200°, то его четвертый угол равен 160°.

Задание 17 № 324943. Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.

Задание 20 № 311541. Объём пирамиды вычисляют по формуле , где - площадь основания пирамиды, - её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?

ВАРИАНТ 3.

Задание 2 № 322293. На координатной прямой отмечены точки A, B, C, D. Одна из них соответствует числу Какая это точка?

В ответе укажите номер правильного варианта.

1) точка A 2) точка B 3) точка C 4) точка D

Задание 3 № 137285. Найдите значение выражения .

Задание 4 № 137383. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

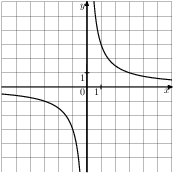
Задание 3 № 203729. Найдите значение по графику функции , изображенному на рисунке.

Задание 7 № 311352. Упростите выражение и найдите его значение при . В ответ запишите полученное число.

Задание 11 № 323436. Найдите площадь треугольника, изображённого на рисунке.

Задание 12 № 311344. На рисунке изображена трапеция. Используя рисунок, найдите косинус угла АВН.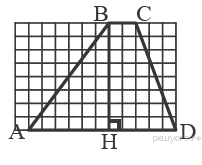

Задание 13 № 169924. Какие из следующих утверждений верны?

1) Сумма углов выпуклого четырехугольника равна 180°.

2) Если один из углов параллелограмма равен 60°, то противоположный ему угол равен 120°.

3) Диагонали квадрата делят его углы пополам.

4) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник - параллелограмм.

Задание 17 № 314914. Человек, рост которого равен 1,8 м, стоит на расстоянии 16 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).

Задание 20 № 311920. Центростремительное ускорение при движении по окружности (в м/c² ) можно вычислить по формуле где - угловая скорость (в с⁻¹), а R - радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с⁻¹, а центростремительное ускорение равно 45 м/c².

ВАРИАНТ 4.

Задание 2 № 205997. Какое из чисел отмечено на координатной прямой точкой A?

1) 2) 3) 4)

Задание 3 № 317389. Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 5 2) 3) 4) 40

Задание 4 № 311446. Найдите корни уравнения .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

Задание 5 № 34. Установите соответствие между графиками функций и формулами, которые их задают.

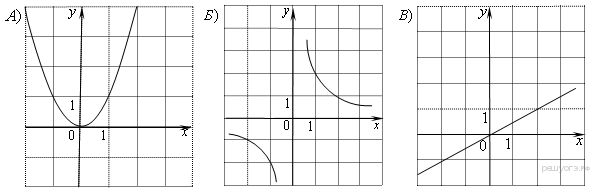
1) 2) 3) 4)

Задание 7 № 311372. Упростите выражение и найдите его значение при . В ответ запишите полученное число.

Задание 11 № 323159. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.

Задание 12 № 311914. Найдите синус острого угла трапеции, изображённой на рисунке.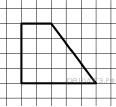

Задание 13 № 169922. Какие из следующих утверждений верны?

1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.

2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.

3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.

4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

Задание 17 № 132754. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 15 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?

Задание 20 № 311337. Длину окружности можно вычислить по формуле , где - радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать ).

ВАРИАНТ 5.

Задание 1 № 206009. Какое из чисел отмечено на координатной прямой точкой A?

1.

2.

3.

4.

Задание 3 № 337339. Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 198 2) 3) 3564 4) 2178

Задание 4 № 314495. Найдите корни уравнения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

Задание 5 № 193097. На одном из рисунков изображена парабола. Укажите номер этого рисунка.

1)

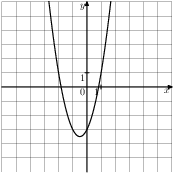
2)

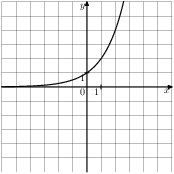
3)

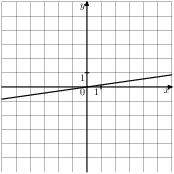
4)

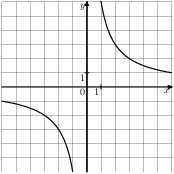
Задание 7 № 311451. Упростите выражение и найдите его значение при . В ответе запишите найденное значение.

Задание 11 № 311957.

Найдите площадь параллелограмма, изображённого на рисунке.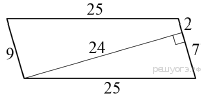

Задание 12 № 311683. Найдите тангенс угла AOB, изображенного на рисунке.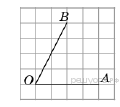

Задание 13 № 169933. Какие из следующих утверждений верны?

1) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

2) Любые два равнобедренных треугольника подобны.

3) Любые два прямоугольных треугольника подобны.

4) Треугольник ABC, у которого AB = 3, BC = 4, AC = 5, является тупоугольным.

Задание 17 № 132755. В 60 м одна от другой растут две сосны. Высота одной 31 м, а другой - 6 м. Найдите расстояние (в метрах) между их верхушками.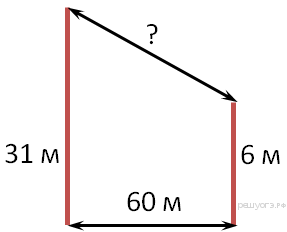

Задание 20 № 311348. Площадь ромба можно вычислить по формуле , где - диагонали ромба (в метрах). Пользуясь этой формулой, найдите диагональ , если диагональ равна 30 м, а площадь ромба 120 м².

ВАРИАНТ 6.

Задание 2 № 157. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?

1) точка M 2) точка N 3) точка P 4) точка Q

Задание 3 № 337462. Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 360 2) 3) 4)

Задание 4 № 314538. Найдите корни уравнения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

Задание 5 № 339114. Установите соответствие между функциями и их графиками. А)

Б)

В)

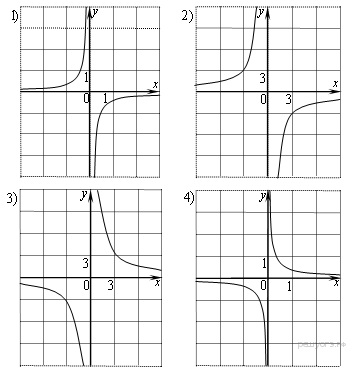
Задание 7 № 311463. Представьте в виде дроби выражение и найдите его значение при . В ответ запишите полученное число.

Задание 11 № 39. Найдите площадь трапеции, изображённой на рисунке.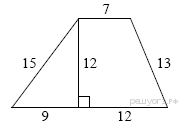

Задание 12 № 196. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.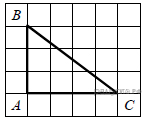

Задание 13 № 169938. Какие из следующих утверждений верны?

1) Площадь многоугольника, описанного около окружности, равна произведению его периметра на радиус вписанной окружности.

2) Если диагонали ромба равна 3 и 4, то его площадь равна 6.

3) Площадь трапеции меньше произведения суммы оснований на высоту.

4) Площадь прямоугольного треугольника меньше произведения его катетов.

Задание 17 № 314820. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?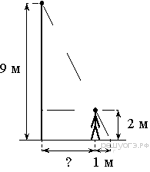

Задание 20 № 311535. Радиус вписанной в прямоугольный треугольник окружности можно найти по формуле , где и - катеты, а - гипотенуза треугольника. Пользуясь этой формулой, найдите , если и .

ВАРИАНТ 7.

Задание 2. № 206005. Какое из чисел отмечено на координатной прямой точкой A?

1.

2.

3.

4.

Задание 3 № 337692. Найдите значение выражения (1,7 · 10^− 5)(2 · 10^− 2).

В ответе укажите номер правильного варианта.

1) 0,0000034 2) 34000000000 3) 0,000000034 4) 0,00000034

Задание 4 № 338915. Решите уравнение

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

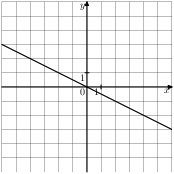
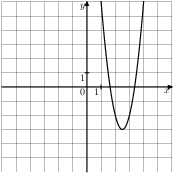
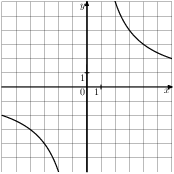
Задание 5 № 201145. На одном из рисунков изображен график функции . Укажите номер этого рисунка.

1)

2)

3)

4)

Задание 7 № 314312. Упростите выражение и найдите его значение при В ответе запишите найденное значение.

Задание 11 № 169840. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.

Задание 12 № 311366. На рисунке изображен параллелограмм. Используя рисунок, найдите синус угла BDC.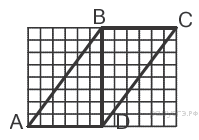

Задание 13 № 311915. Укажите номера верных утверждений.

1) Площадь трапеции равна половине высоты, умноженной на разность оснований.

2) Через любые две точки можно провести прямую.

3) Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.

Задание 17 № 132752. Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?

Задание 20 № 311528. Площадь треугольника можно вычислить по формуле , где - сторона треугольника, - высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону , если площадь треугольника равна , а высота равна 14 м.

ВАРИАНТ 8.

Задание 2 № 314153. Одна из точек, отмеченных на координатной прямой, соответствует числу Какая это точка?

1) точка A 2) точка B 3) точка C 4) точка D

Задание 3 № 337700. Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 2) 3) 4) 90

Задание 4 № 341350. Решите уравнение 8x² − 12x + 4 = 0. Если корней несколько, запишите их через точку с запятой в порядке возрастания.

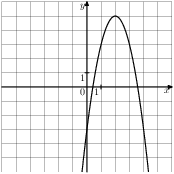
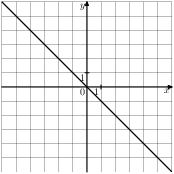
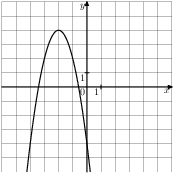
Задание 5 № 201295. На одном из рисунков изображена парабола. Укажите номер этого рисунка.1.

2.

3.

4.

Задание 7 № 314315. Упростите выражение и найдите его значение при и В ответе запишите найденное значение.

Задание 11 № 323445. Найдите площадь треугольника, изображённого на рисунке

Задание 12 № 40. Найдите тангенс угла AOB, изображенного на рисунке.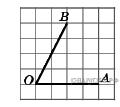

Задание 13 № 314814. Какие из данных утверждений верны? Запишите их номера.

1) Вокруг любого треугольника можно описать окружность.

2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм - квадрат.

3) Площадь трапеции равна произведению средней линии на высоту.

Задание 17 № 70. От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.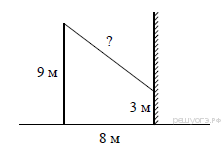

Задание 20 № 311530. Площадь трапеции можно вычислить по формуле , где - основания трапеции, - высота (в метрах). Пользуясь этой формулой, найдите высоту , если основания трапеции равны и , а её площадь .

ВАРИАНТ 9.

Задание 2 № 105. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?

1) точка А 2) точка В 3) точка С 4) точка D

Задание 3 № 341194. Найдите значение выражения

В ответе укажите номер правильного варианта.

1) 2600000 2) 0,000026 3) 0,0000026 4) 0,00026

Задание 4 № 311439. Решите уравнение .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

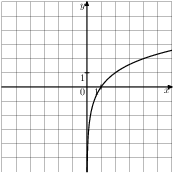
Задание 5 № 202195. На одном из рисунков изображена гипербола. Укажите номер этого рисунка. 1)

2)

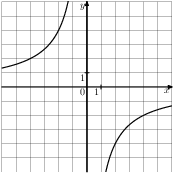
3)

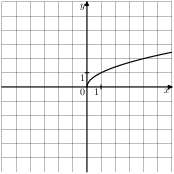
4)

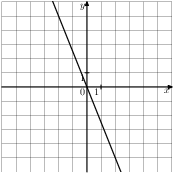
Задание 7 № 341704. Найдите значение выражения

при a = 7,7.

Задание 11 № 65. Найдите площадь параллелограмма, изображённого на рисунке.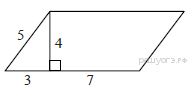

Задание 12 № 92. Найдите тангенс угла B треугольника ABC, изображённого на рисунке.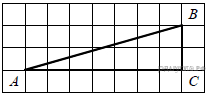

Задание 13 № 314818. Какие из данных утверждений верны? Запишите их номера.

1) Каждая из биссектрис равнобедренного треугольника является его медианой.

2) Диагонали прямоугольника равны.

3) У любой трапеции боковые стороны равны.

Задание 17 № 311509. Глубина крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.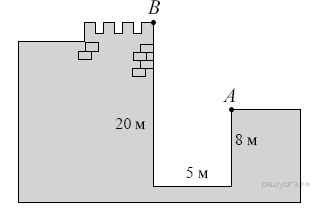

Задание 20 № 338052. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R, где I - сила тока (в амперах), R - сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 180 Вт, а сила тока равна 6 А.

ВАРИАНТ 10.

Задание 2 № 314157.) Одна из точек, отмеченных на координатной прямой, соответствует числу Какая это точка?

1) точка M 2) точка N 3) точка P 4) точка Q

Задание 3 № 341700.) Найдите значение выражения 1)

2) −5

3)

4) 5

Задание 4 № 338958. ) Найдите корни уравнения

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

Задание 5 № 314772.) Установите соответствие между графиками функций и формулами, которые их задают.

А)

Б)

В)

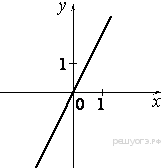
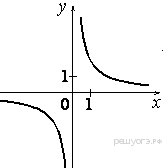
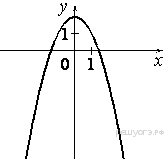
1)

2)

3)

Задание 7 № 311352.) Упростите выражение и найдите его значение при . В ответ запишите полученное число.

Задание 11 № 311682.) Найдите площадь трапеции, изображённой на рисунке.

Задание 12 № 40.) Найдите тангенс угла AOB, изображенного на рисунке.

Задание 13.)

Задание 17 № 132764). Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?

Задание 20 № 338089.) Закон Джоуля-Ленца можно записать в виде Q = I²Rt, где Q - количество теплоты (в джоулях), I - сила тока (в амперах), R - сопротивление цепи (в омах), а t - время (в секундах). Пользуясь этой формулой, найдите время t (в секундах), если Q = 2187 Дж, I = 9 A,R = 3 Ом.

1 вариант (ΙΙ часть)

22.

23.

24.

25.

2 вариант (ΙΙ часть)

22.

23.

24.

25.