- Учителю
- Урок-зачет по теме: “Первообразная и интеграл.”
Урок-зачет по теме: “Первообразная и интеграл.”
МОУ Ветлужская школа №1
Урок-зачет по теме:
"Первообразная и интеграл."
Дисциплина : «Математика»
(групповая форма организации деятельности учащихся)
Автор: Назарова О.Н.,
учитель математики
Рассмотрено на
заседании МО__________
г. Ветлуга,2015г.
Счастливый случай.
Тема: Первообразная и интеграл.
Цель зачета: 1) проверка уровня обладания учащимися изученного материала по данной теме.
2) способность учащихся реализовать полученные знания при выполнение заданий различного уровня сложности.
3) формирования у учащихся таких черт личности как чувство взаимоответственности и самоутверждения, самоанализа, самооценки.
Метод проведения: урок-зачет в форме игры «Счастливый случай».
Оборудование: сигнальные часы, карточки с заданиями, листы учета знаний семьи (индивидуальный). На доске табло по подведению каждого гейма, цветные мелки.
Ход урока
Организационный момент
Группа делится на 4 «семьи», выбирается глава «семьи» (до начала занятия). «Семьи» садятся за свои столы.
На столе каждой «семьи» лежит «Лист учета знаний», где глава «семьи» напротив каждой фамилии ставит (в случае правильного ответа) знак «+».
По итогам каждого гейма подсчитываются знаки «+» и в строке «Всего» ставится их количество на «семью».
В строке напротив фамилии суммируются знаки «+» и можно выставить оценку каждому за работу на уроке.
Лист учета знанийп/п
Ф.И.
Геймы
Сумма плюсов
Оценка за урок
I
II
III
IV
V
1
2
3
4
5
6
7
Всего
Первый гейм «Разминка»
Отгадывание кроссворда. Здесь учащиеся должны показать свои теоретические знания на минимальном уровне. Кроссворд пишется на отдельных листах и выдается каждой «семье». За каждое правильно угаданное слово «семья» получает 1 балл. Это задание на скорость и «семья», которая первая отгадала кроссворд, получает 4 дополнительных балла.
Максимальное число баллов, которое может получить «семья», равно 16.
Время выполнения задания - 5 минут.
В листе учета знаний ставится в строке «Всего» число баллов, заработанных «семьей». Этот результат заносится в табло на доске.
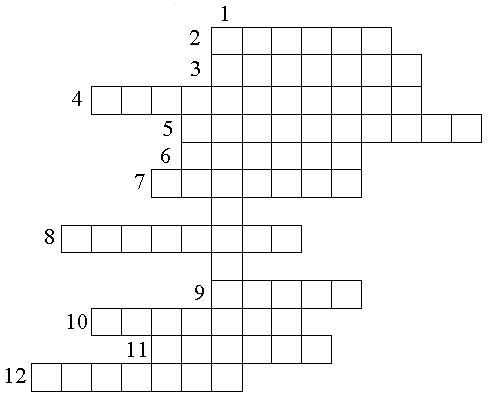
1. Как называется функция F(x)?
2. Что является графиком функции у=ах+b?
3. Самая низкая школьная оценка.
4. Какой урок обычно проходит перед зачетом?
5. Синоним слова дюжина?
6. Есть в каждом слове, у растения и может быть у уравнения.
7. Что можно вычислить при помощи интеграла?
8. Одно из важнейших понятий математики.
9. Форма урока, на котором проводится проверка знаний.
10.Немецкий ученый, в честь которого названа формула,
связывающая площадь криволинейной трапеции и интеграл.
11. Множество точек плоскости с координатами (x, f(x)), где х пробегает область определения функции f.
12.Соответствие между множествами Х и Y, при котором каждому значению множества Х поставлено в соответствие единственное значение из множества Y, носит название ....
Ответы: 1. Первообразная. 2. Прямая. 3. Единица. 4. Контроль. 5. Двенадцать. 6. Корень. 7. Площадь. 8. Интеграл. 9. Зачет. 10. Лейбниц. 11. График. 12. Функция.
Второй гейм «Дальше, дальше…»
Это гейм индивидуальный, т.е. каждый учащийся пишет ответы в своей тетради. Время выполнения задания - 15 мин. По окончании этого времени учитель зачитывает ответы. Учащиеся у себя в тетрадях обводят правильный ответ в кружок и подсчитывают количество кружков (столько плюсов ставят главы «семей» в «Лист учета знаний»), и каждый получает оценку за этот этап. Главы «семей» подсчитывают средний балл и сообщают преподавателю, который ставит эти данные в табло.
1. Что называется первообразной?
2. Как читается основное свойство первообразной?
3. Как можно вычислить площадь криволинейной трапеции при помощи интеграла?
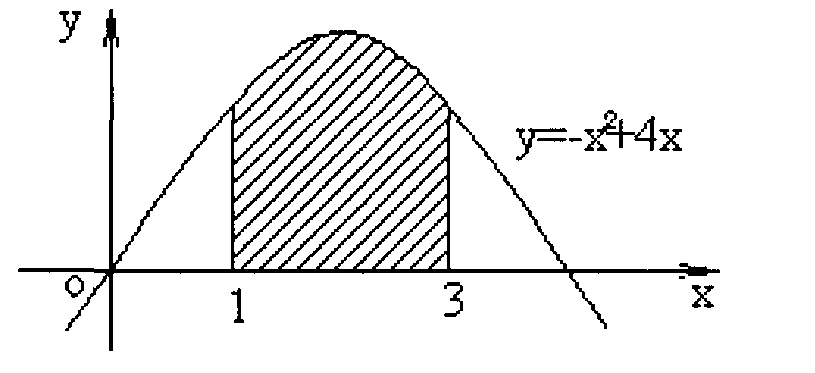
4. Запишите с помощью интеграла площадь фигуры изображенной на рисунке:
5. Найти первообразные для функций: а) 10х; б) х2; в) -sin(2x);
г) cosx; д) х4; е) 3х2.
6. Истинны ли равенства:
а) 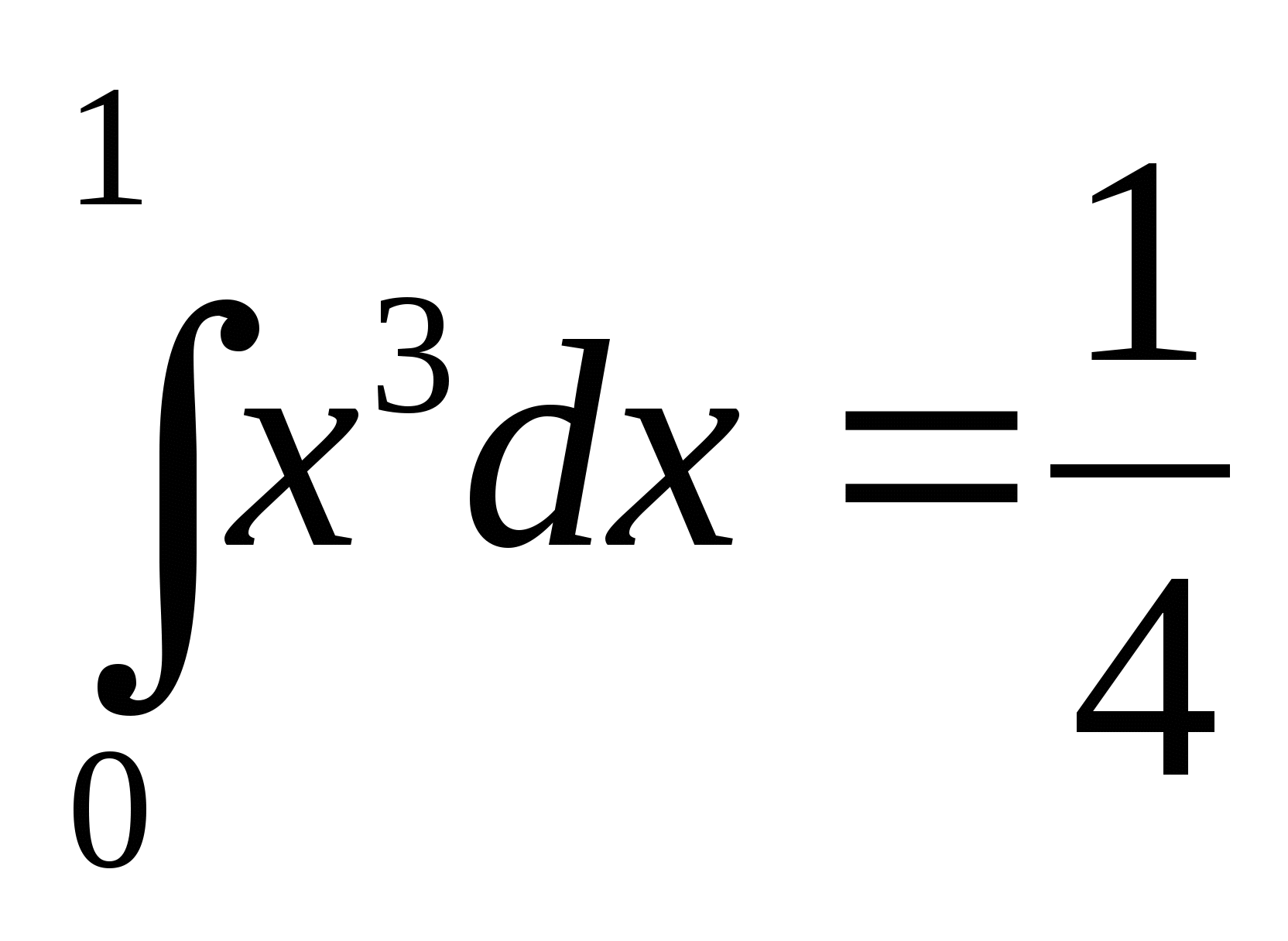 ; б)
; б) 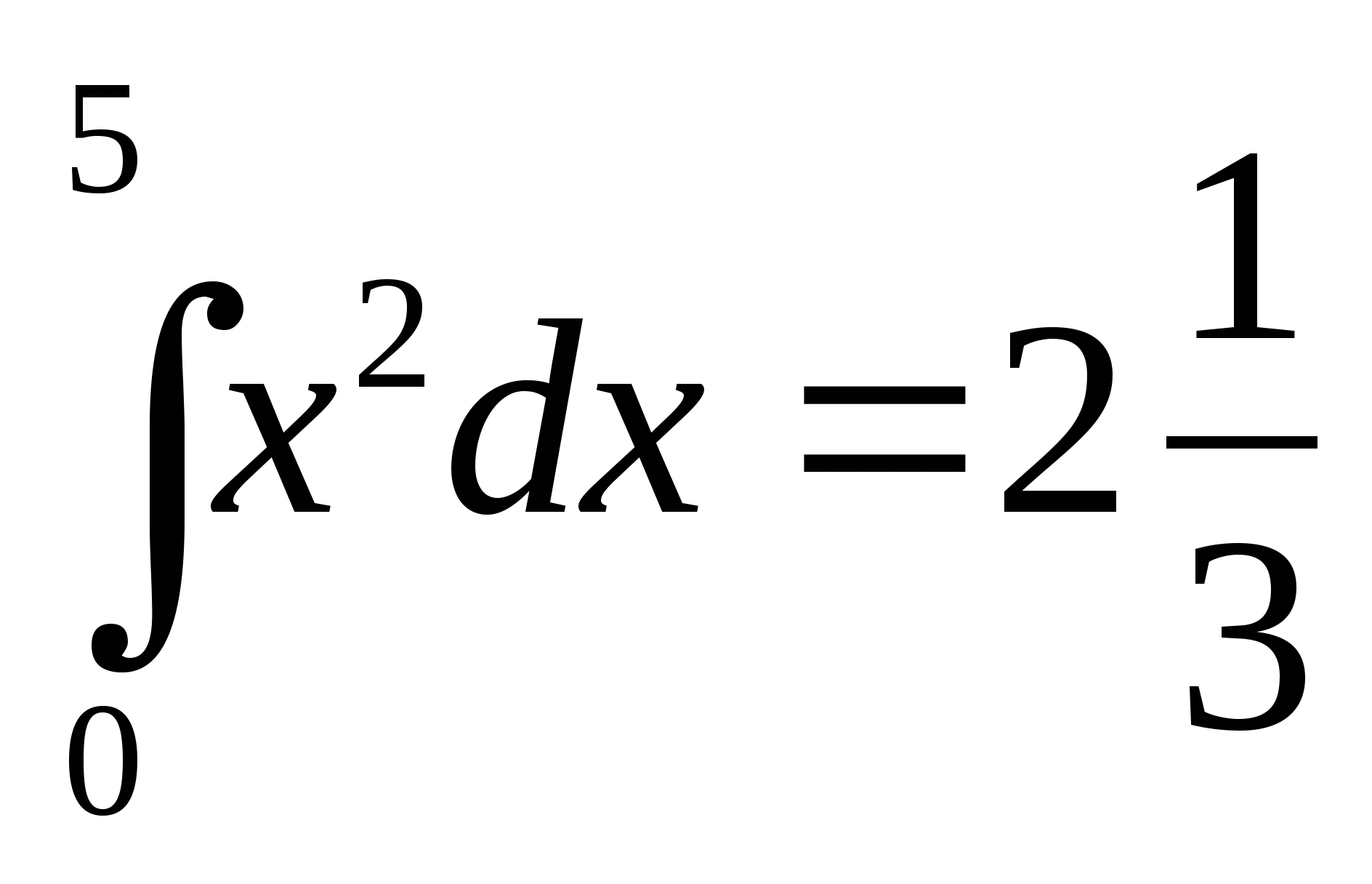 ; в)
; в) ![]() ;
;
г) 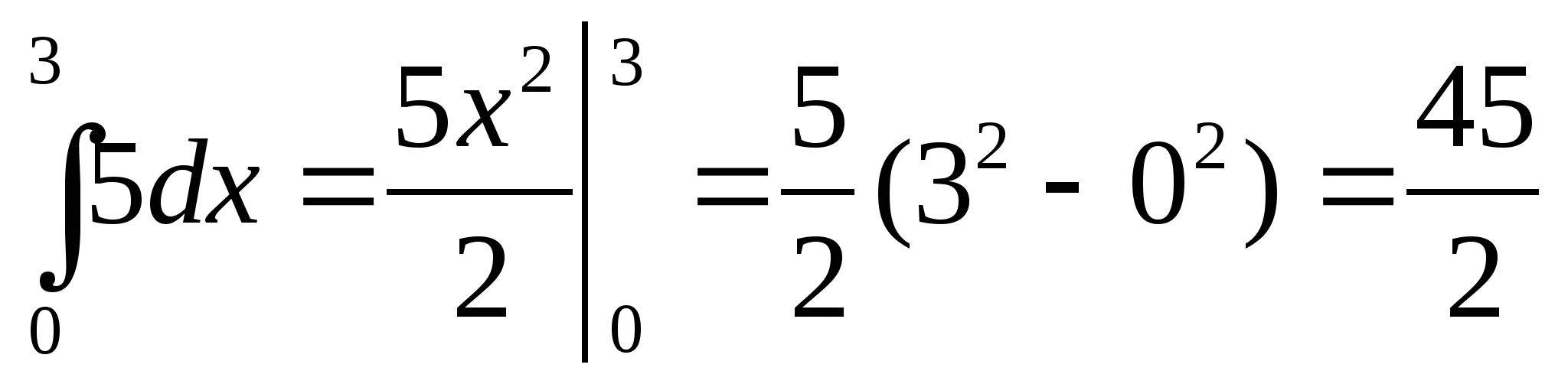 ;
;
д) 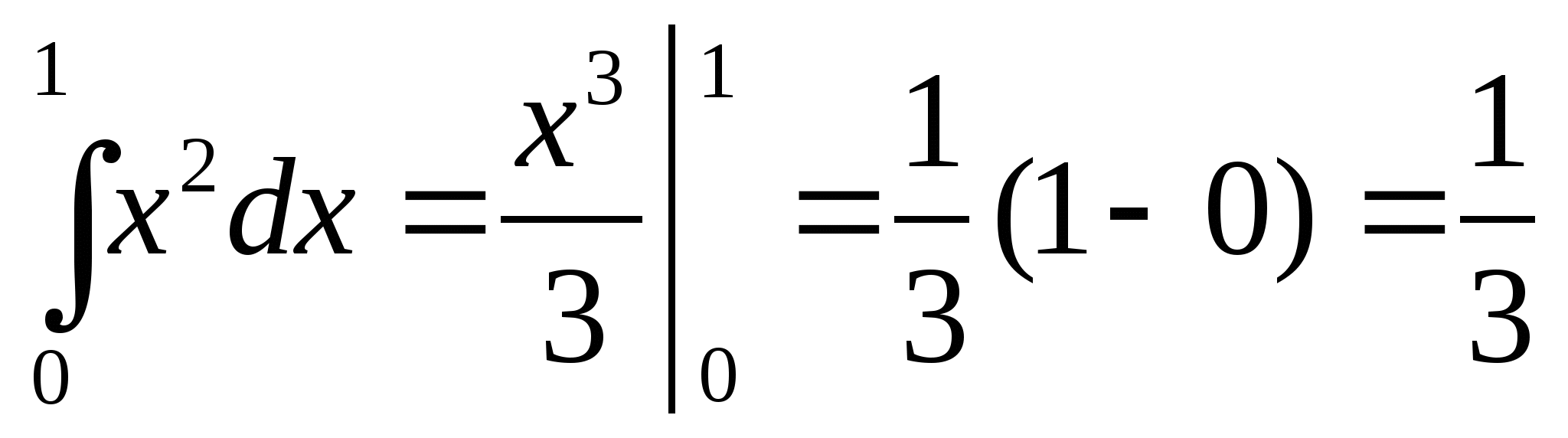 ;
;
е) 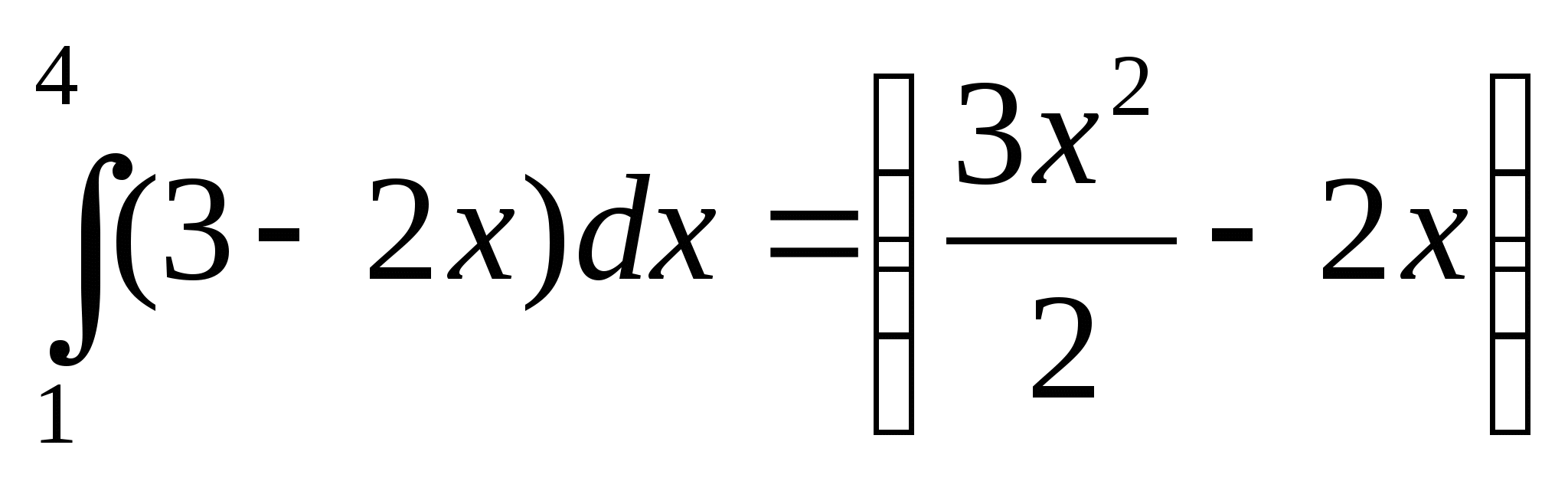 ?
?
Ответы:
1. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка F'(х) = f(х).
2. Любая первообразная для функции f на промежутке может быть записана в виде F(х)+С, где F(х) одна из первообразных для функции f(x) на заданном промежутке, а С произвольная постоянная.
3. 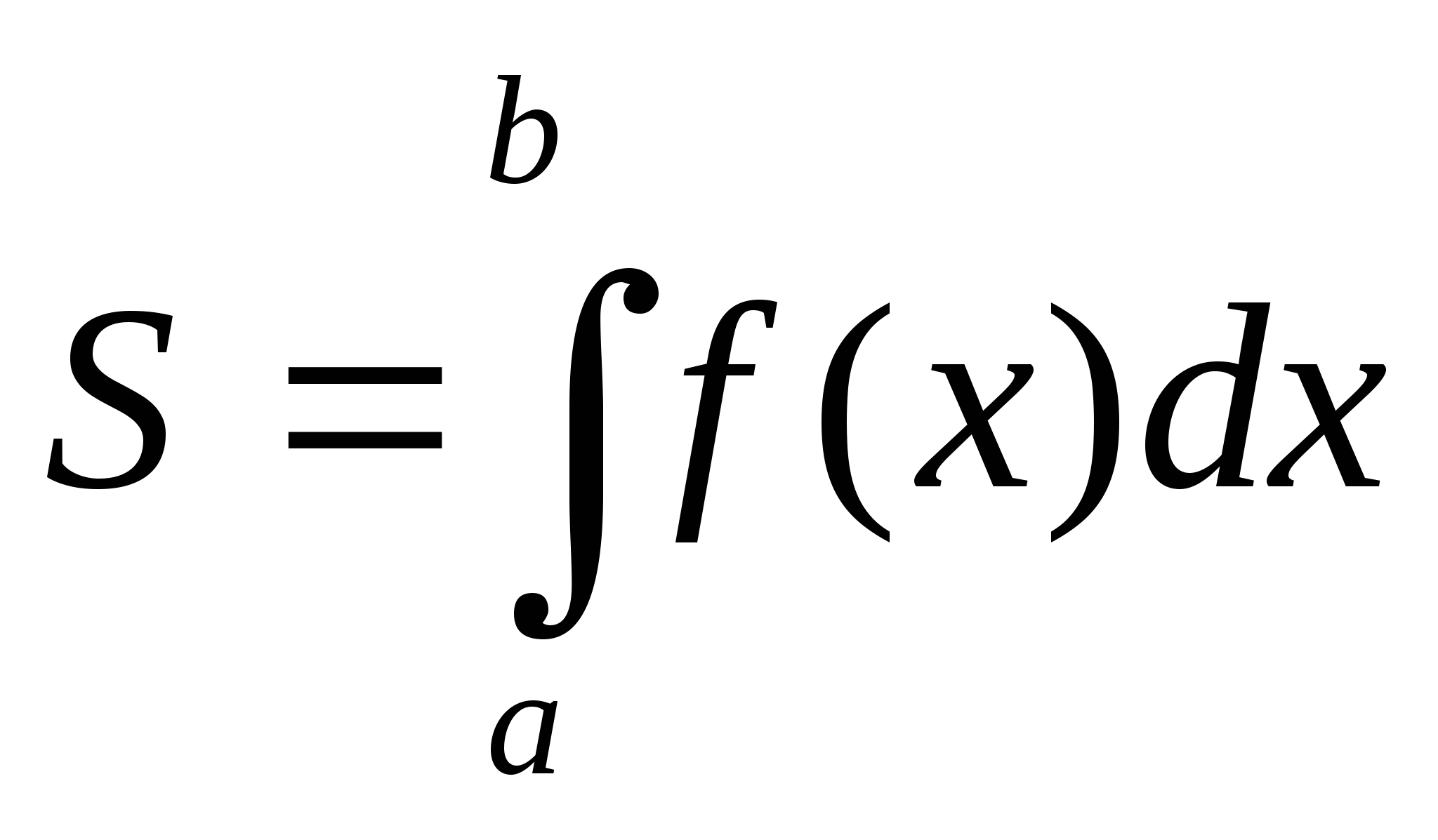
4. ![]()
5. а) 5x2+ C; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
x3+C.
; е)
x3+C.
6. а) истинно; б) ложно; в) ложно; г) ложно; д) истинно; е) ложно.
Третий гейм «Спешите видеть»
Каждая «семья» получает карточку с заданием. 1 и 3 «семьи» получают одинаковые карточки, 2 и 4 -тоже. Это задание на скорость и оно выполняется на отдельных листах. Время выполнения задания 5 минут. «Семья», первая выполнившая задание, получает 1 дополнительный балл. За правильное выполнение задания «семья» получает 1 балл. В задании требуется изобразить криволинейную трапецию, ограниченную:
а) графиком функции у =4х - х2, осью ОХ и прямой у=4 - х;
б) графиком функции у = 4 - х2, осью ОХ и прямой у=4 - х.
О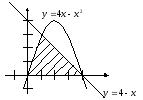
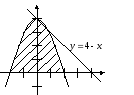 твет: а) x б) x
твет: а) x б) x
4 4
![]()
1 y=0 1 y=0
0 1 4 y -2 -1 0 1 2 4 y
Четвертый гейм «Составьте фразу»
Каждой «семье» выдается 7 карточек, на каждой из которых написано по 4 интеграла. Задача «семьи»: вычислить все 28 интегралов; найти на доске правильный ответ, под которым написана буква. Сопоставив результат вычисления интеграла и букву, учащиеся должны получить фразу. «Семья», которая первая отгадает фразу, получает дополнительный балл. Баллы начисляются команде за каждую правильно найденную букву. Время выполнения задания 20 минут.
Задание
Вычислите интеграл:
1) ![]() ; 2)
; 2) 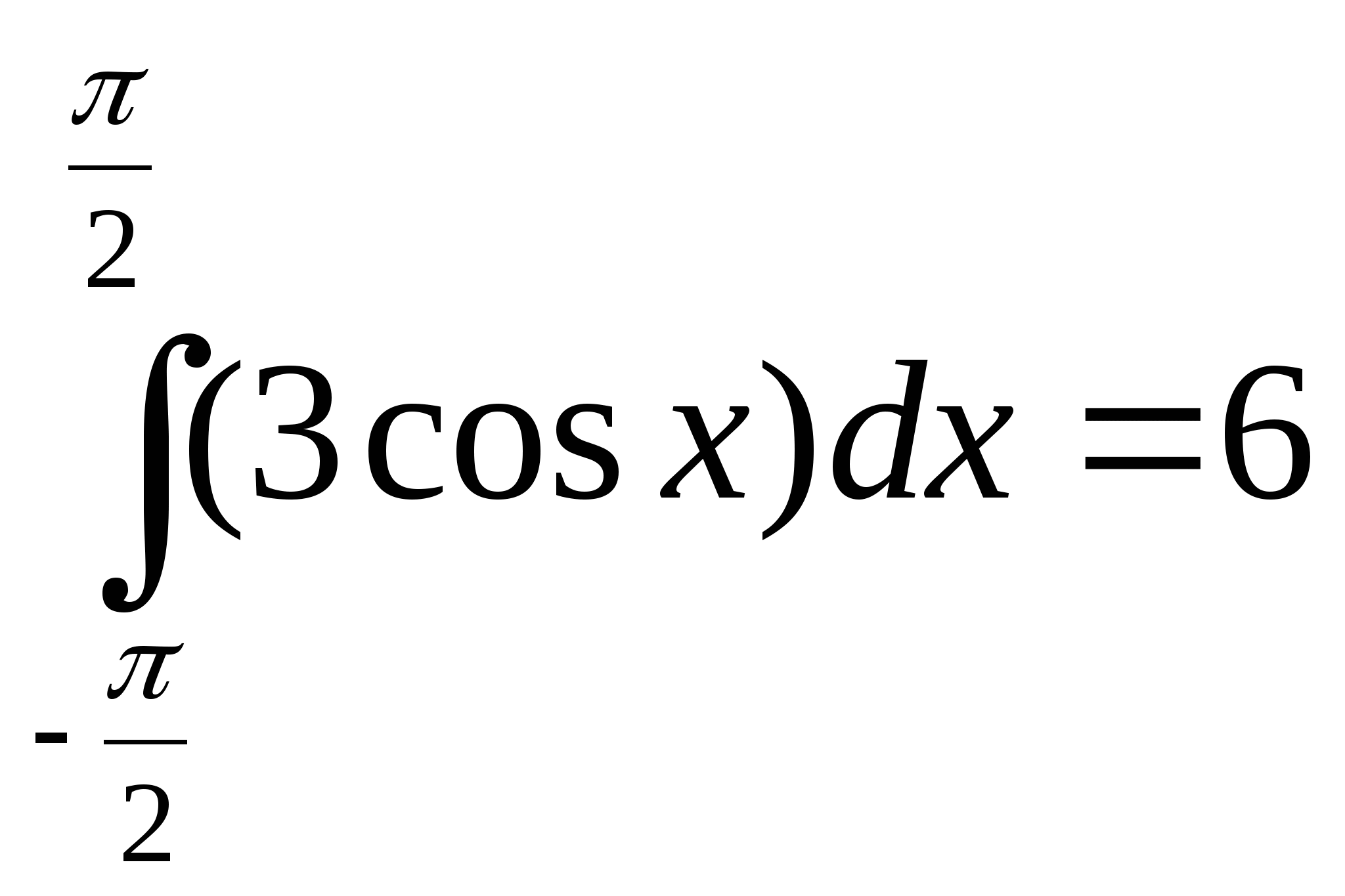 ; 3)
; 3) ![]() ; 4)
; 4) 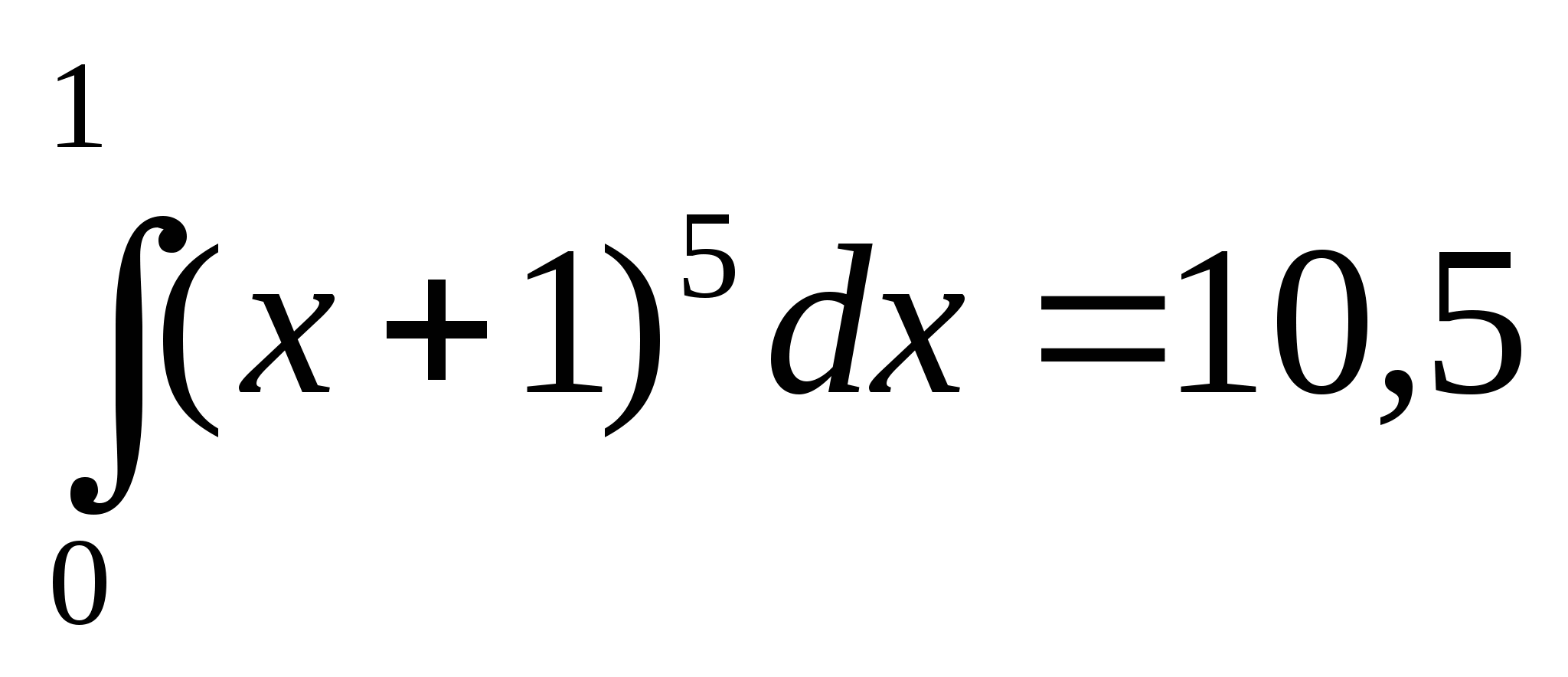
5) 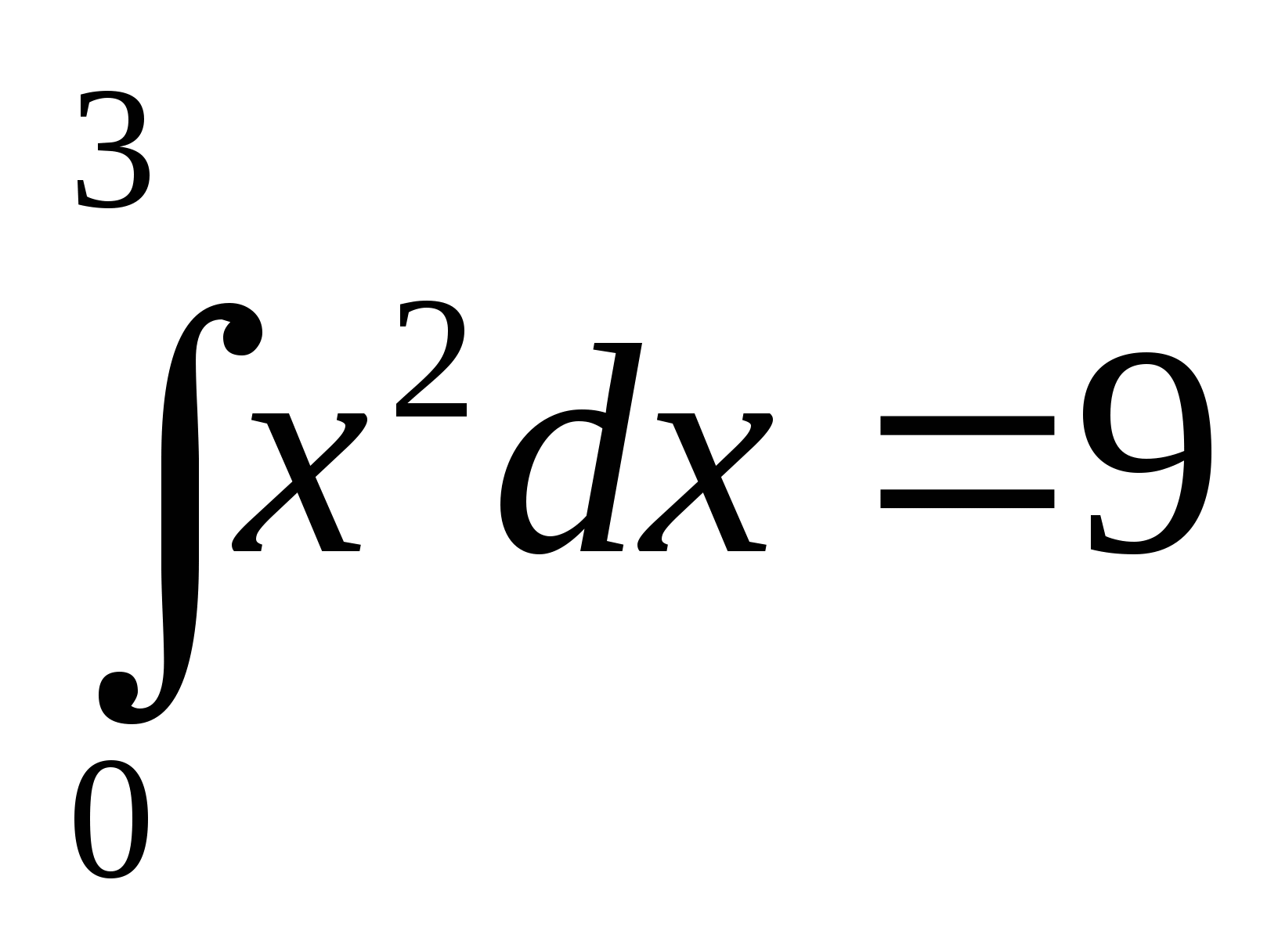 ; 6)
; 6) 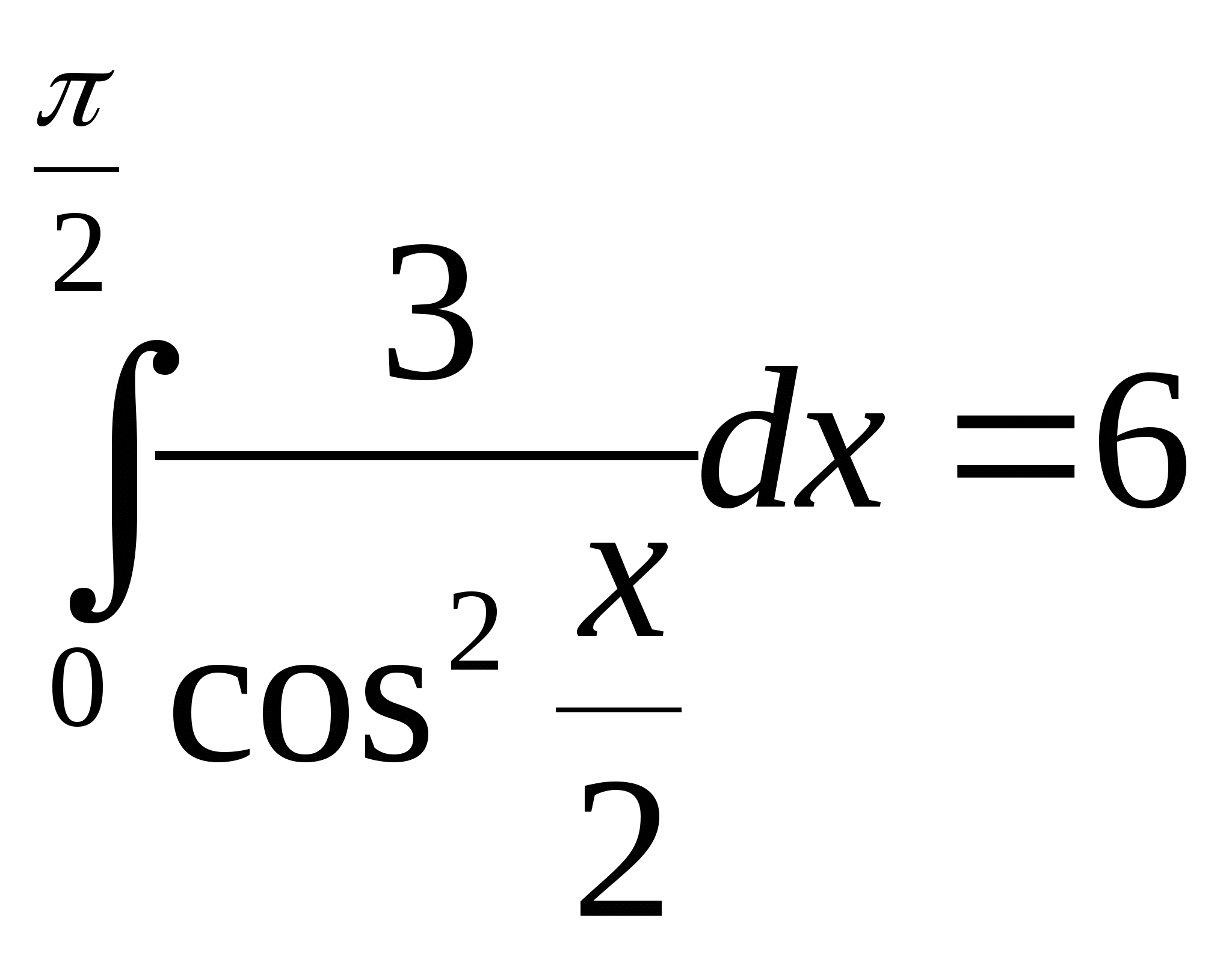 ; 7)
; 7) 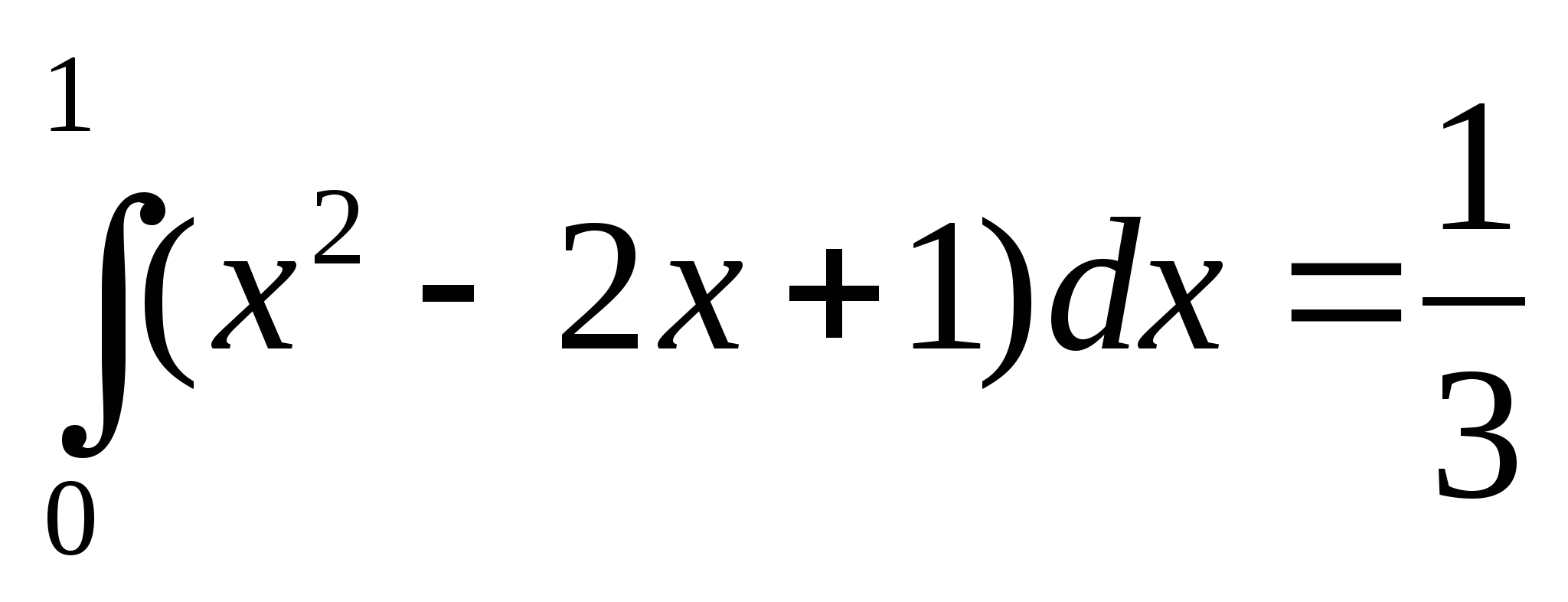 ; 8)
; 8) 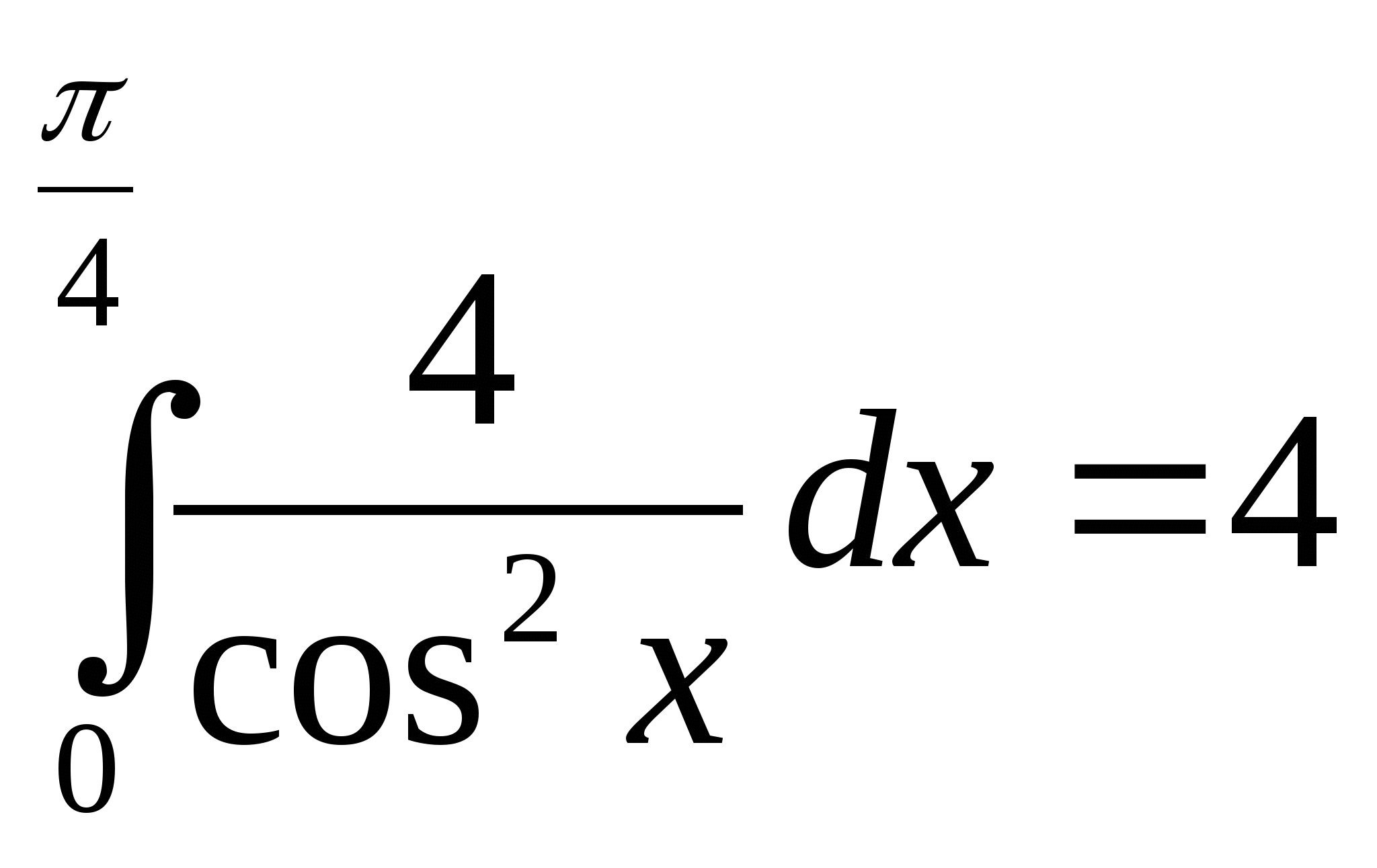
9) 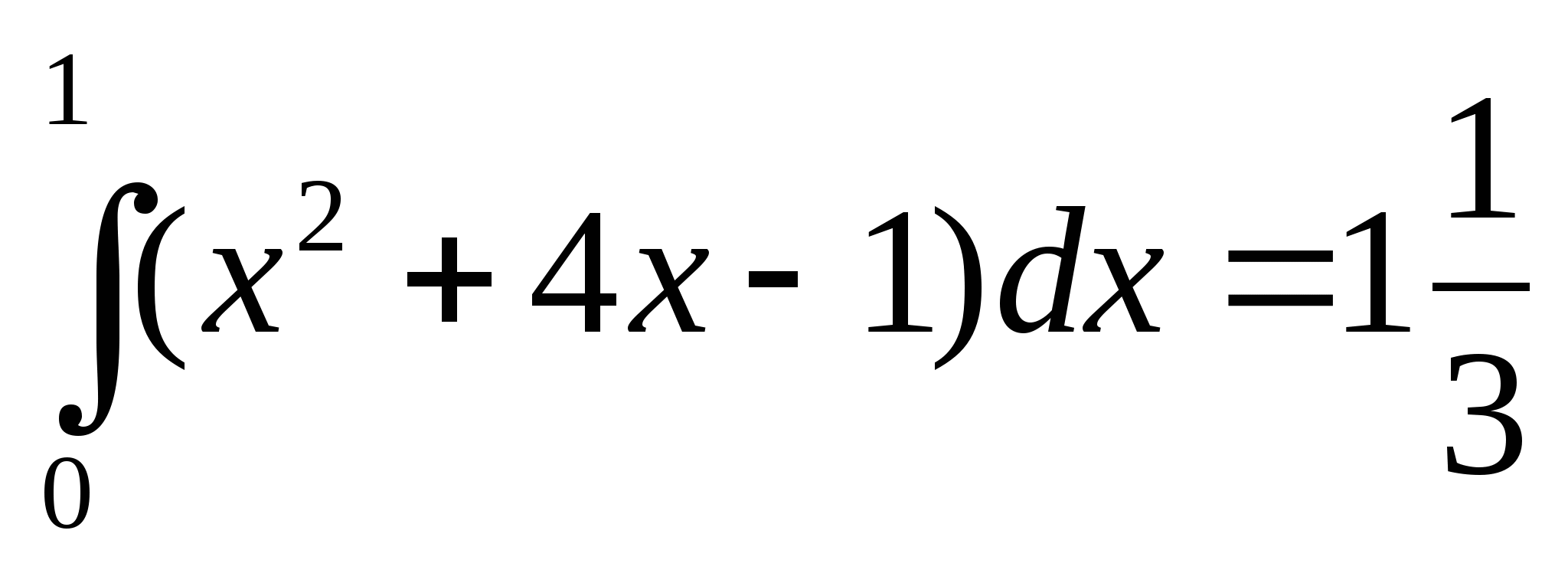 ; 10)
; 10) 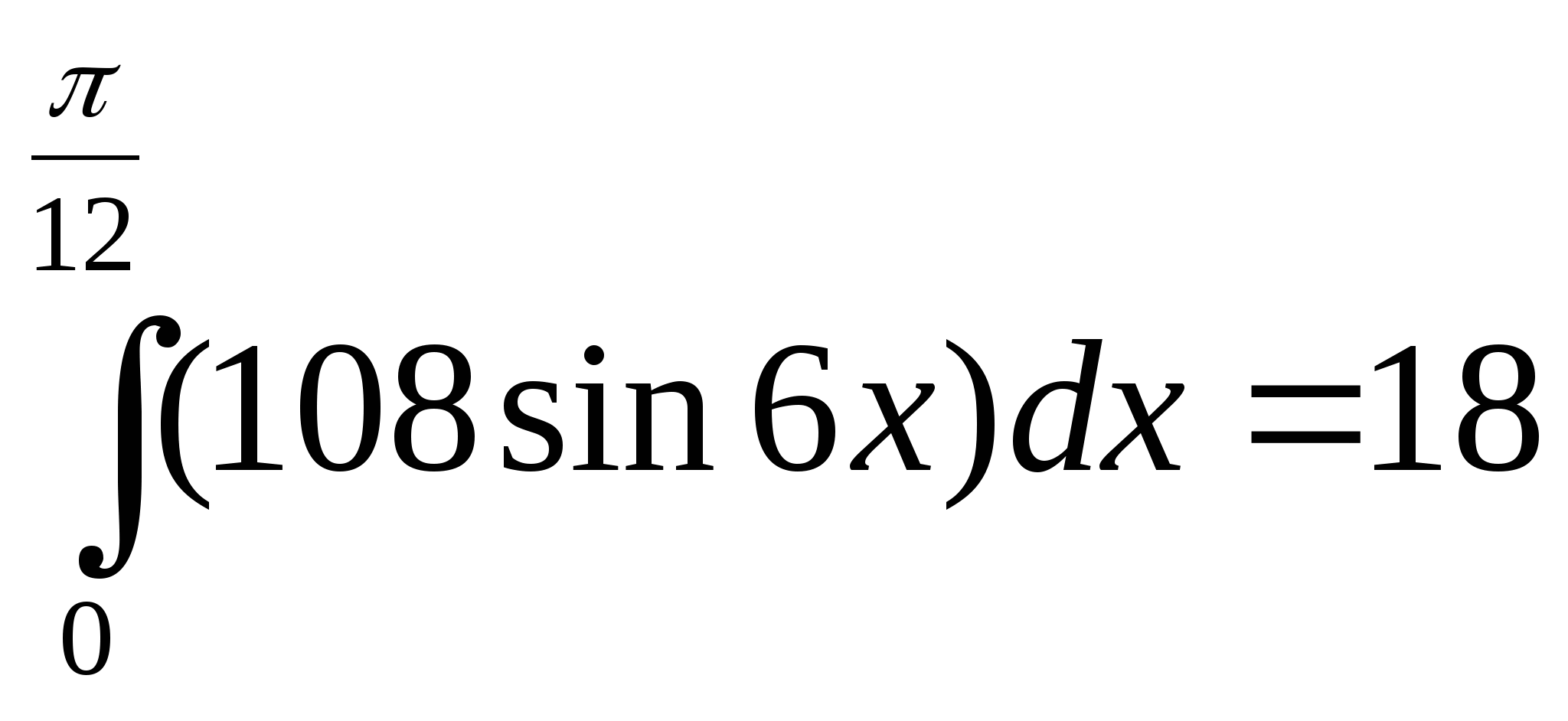 ;
;
11) 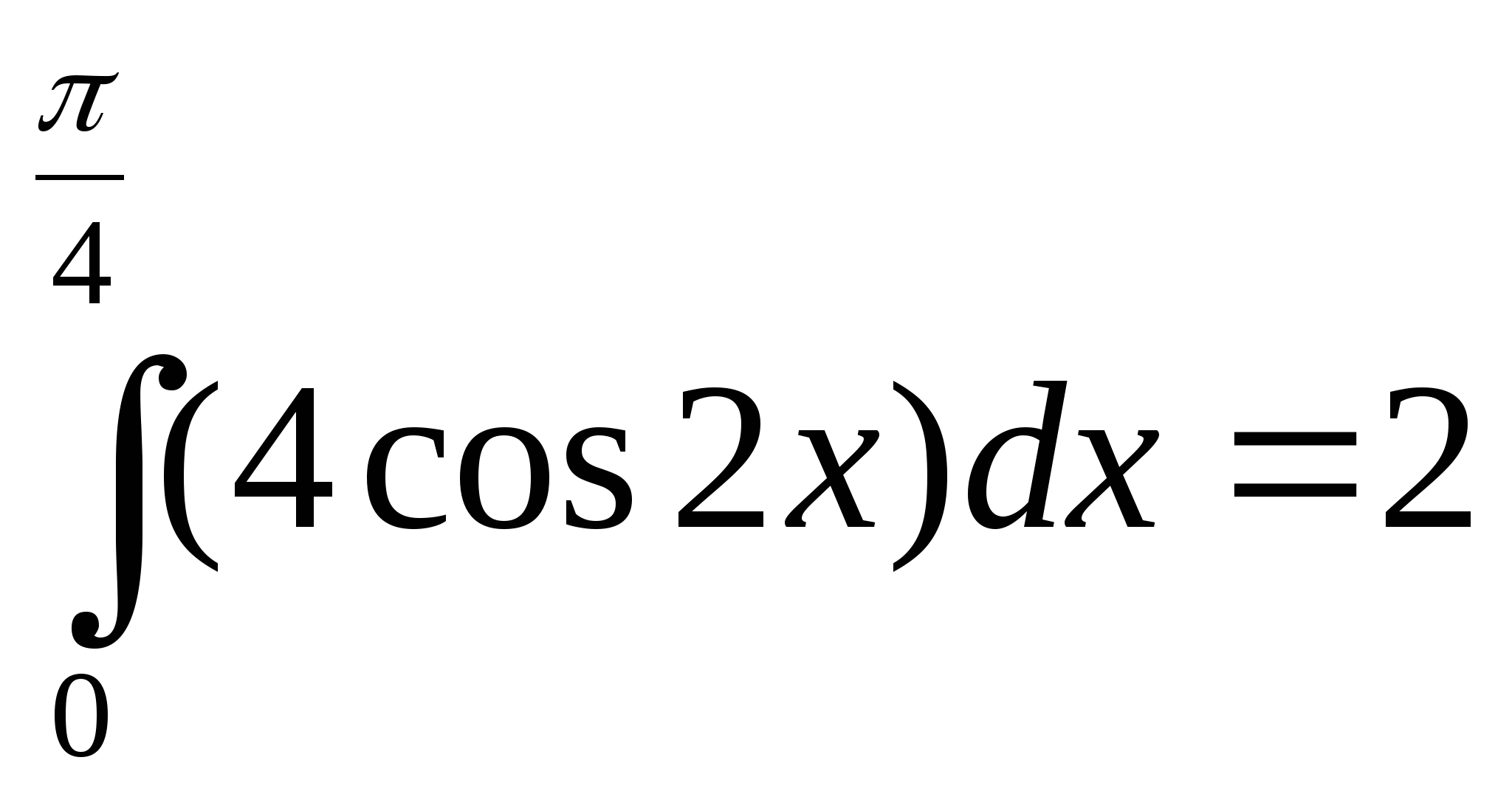 ; 12)
; 12) 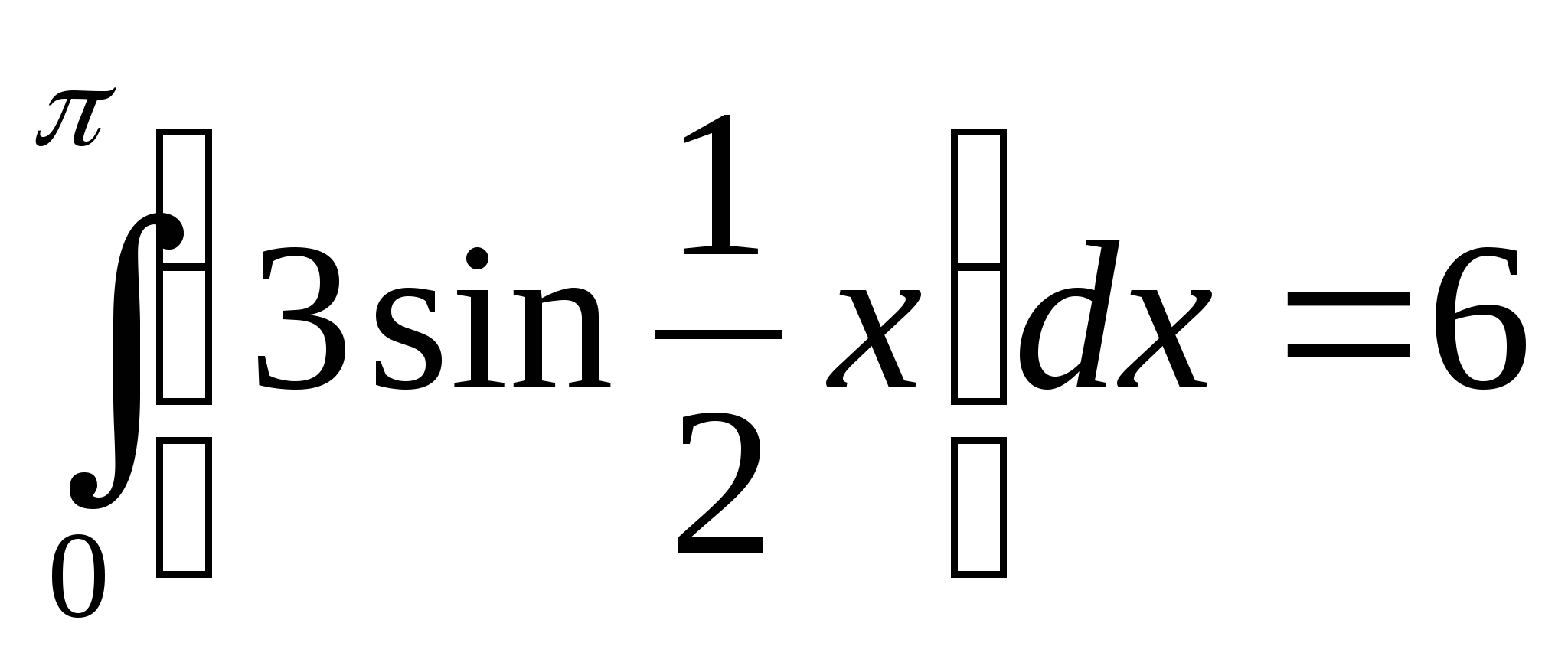
13) ![]() ; 14)
; 14) ![]() ;
;
15) 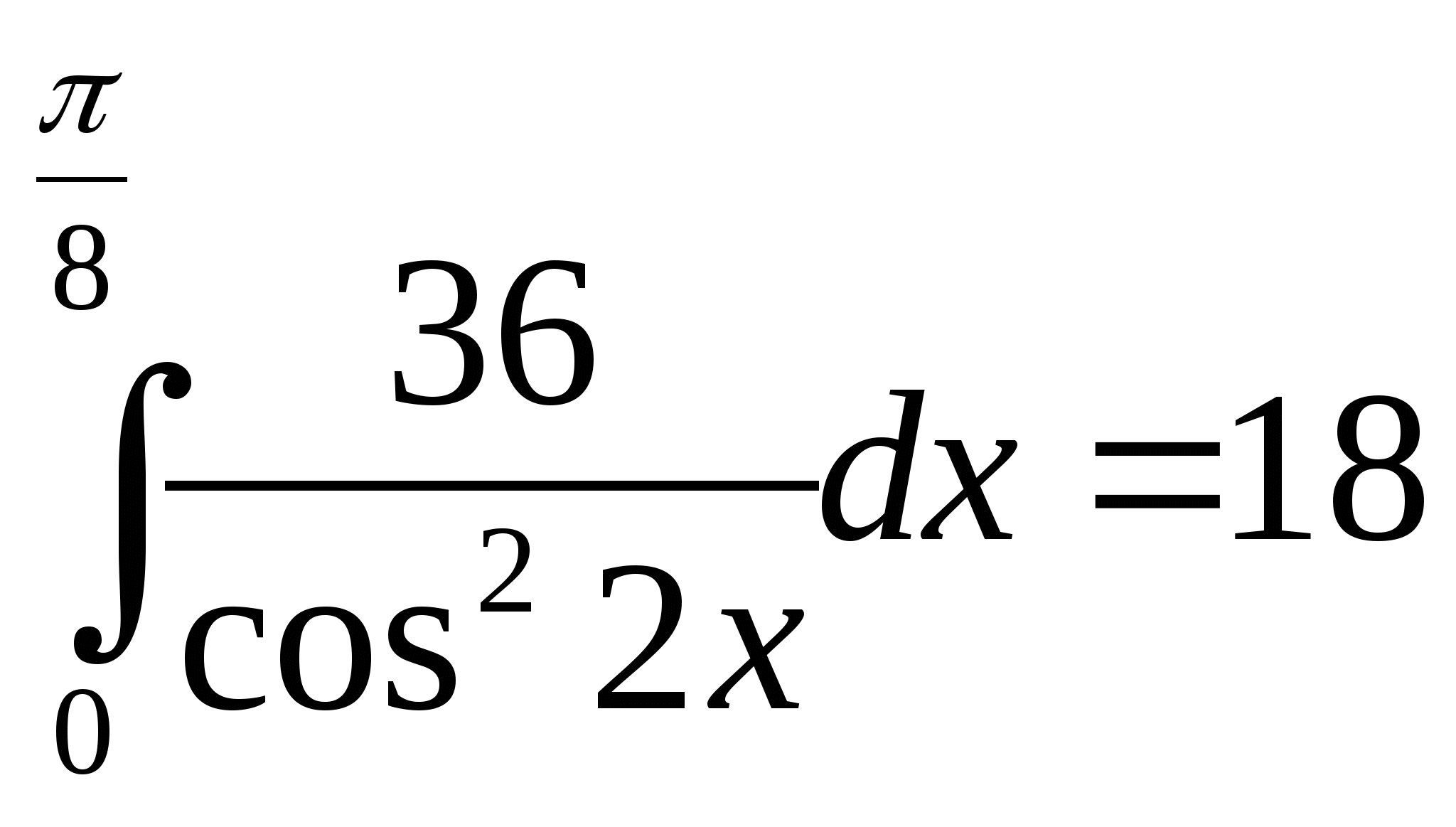 ; 16)
; 16) 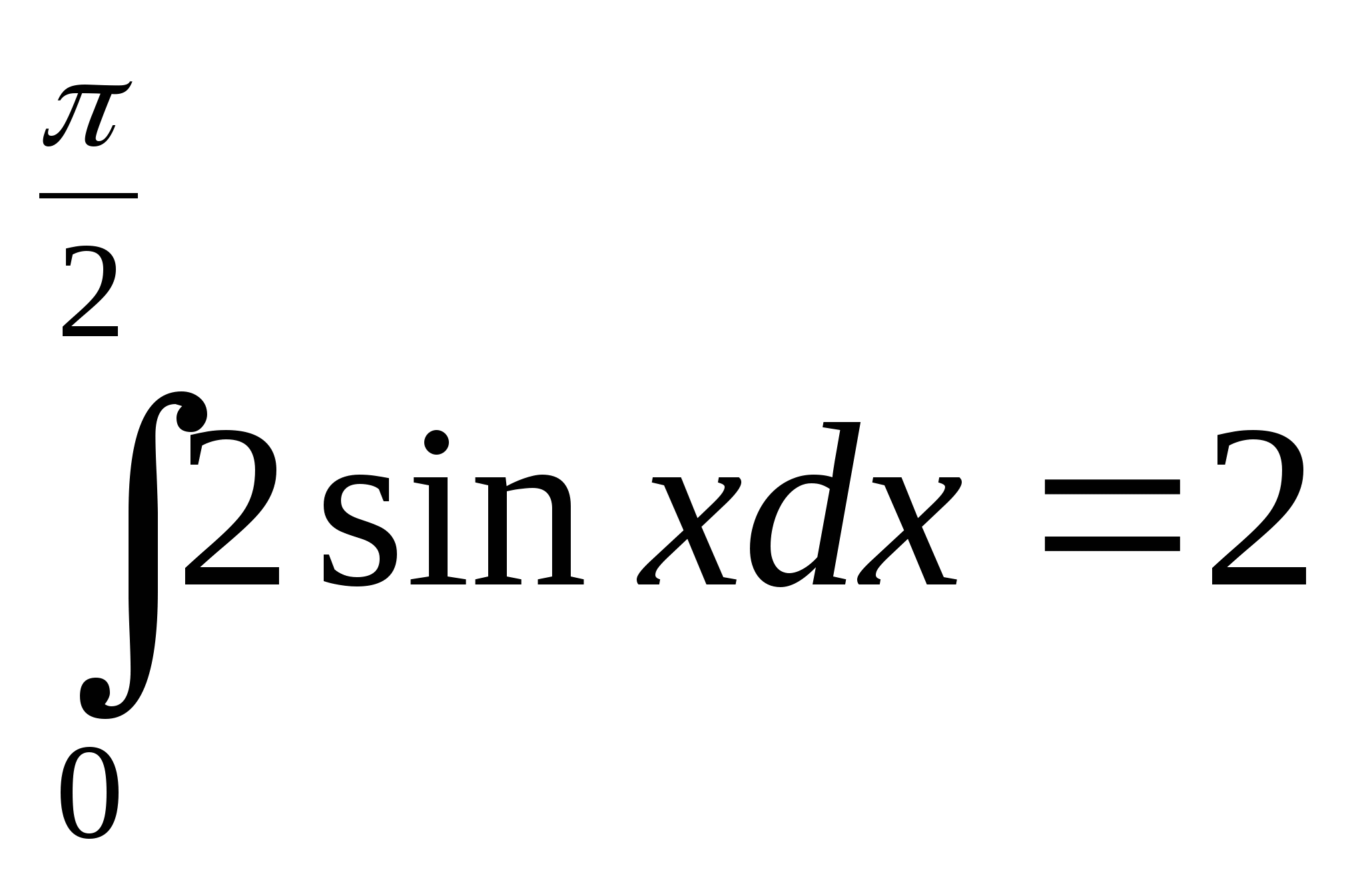 ;
;
17)![]() ; 18)
; 18) ![]() ; 19)
; 19) 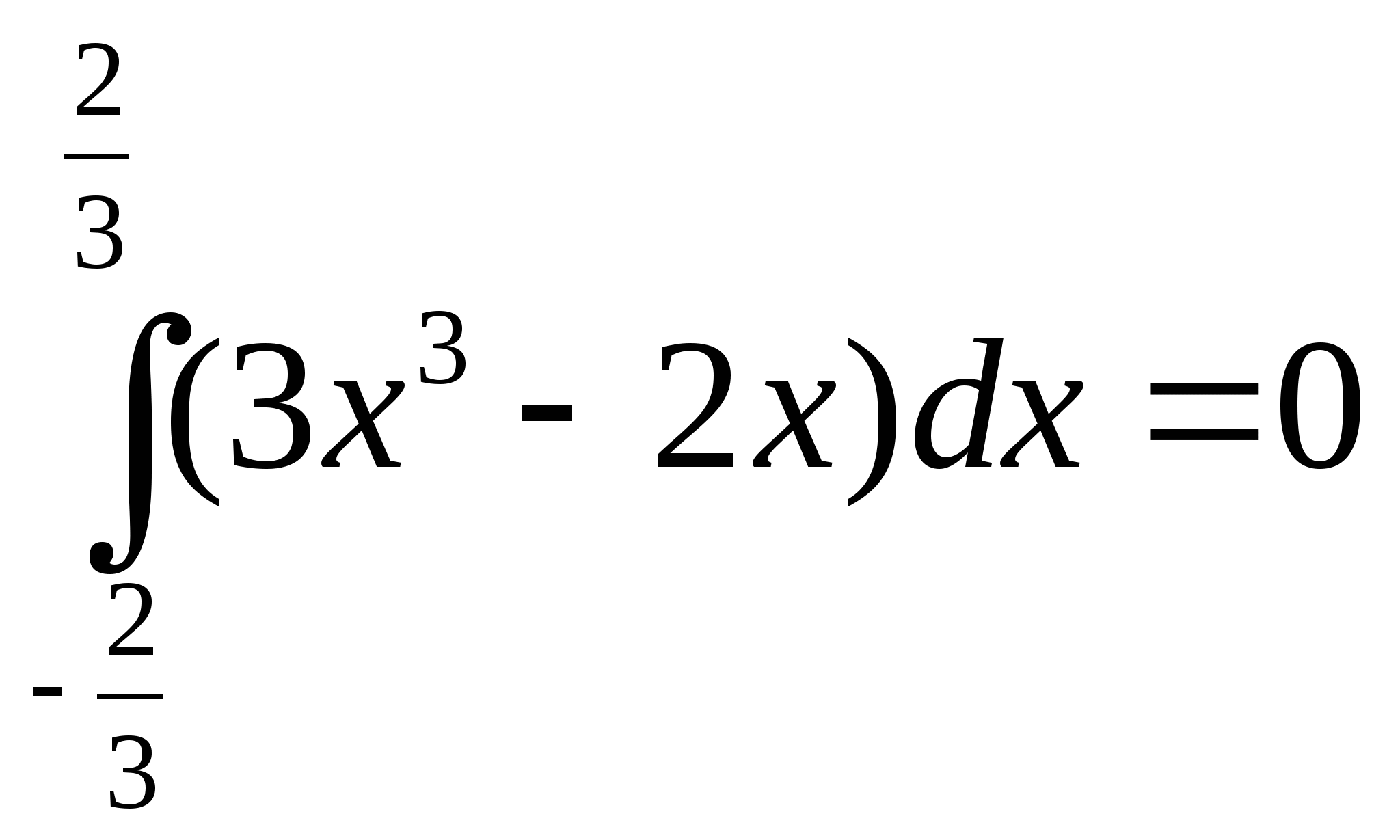 ; 20)
; 20) 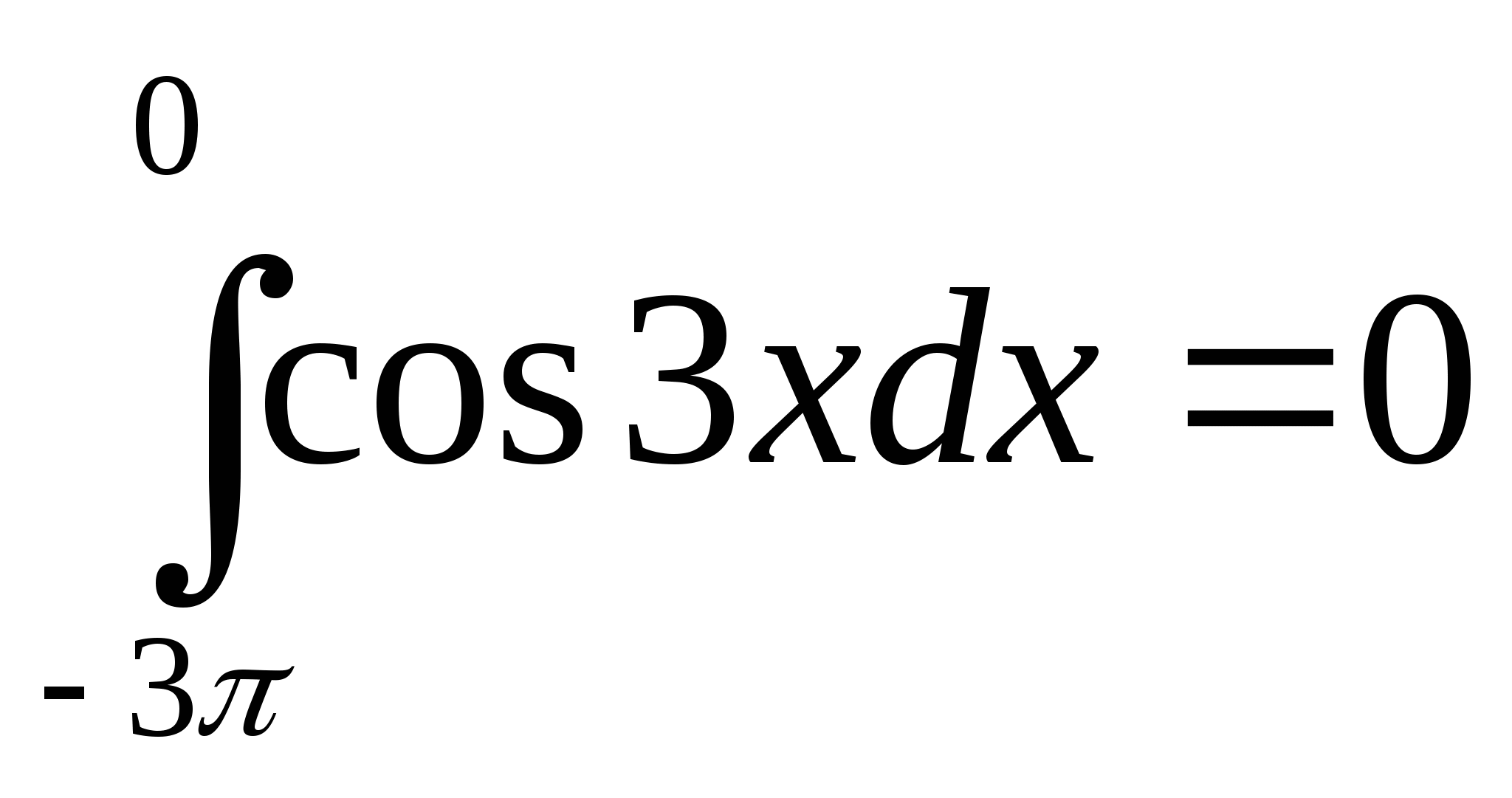
21) 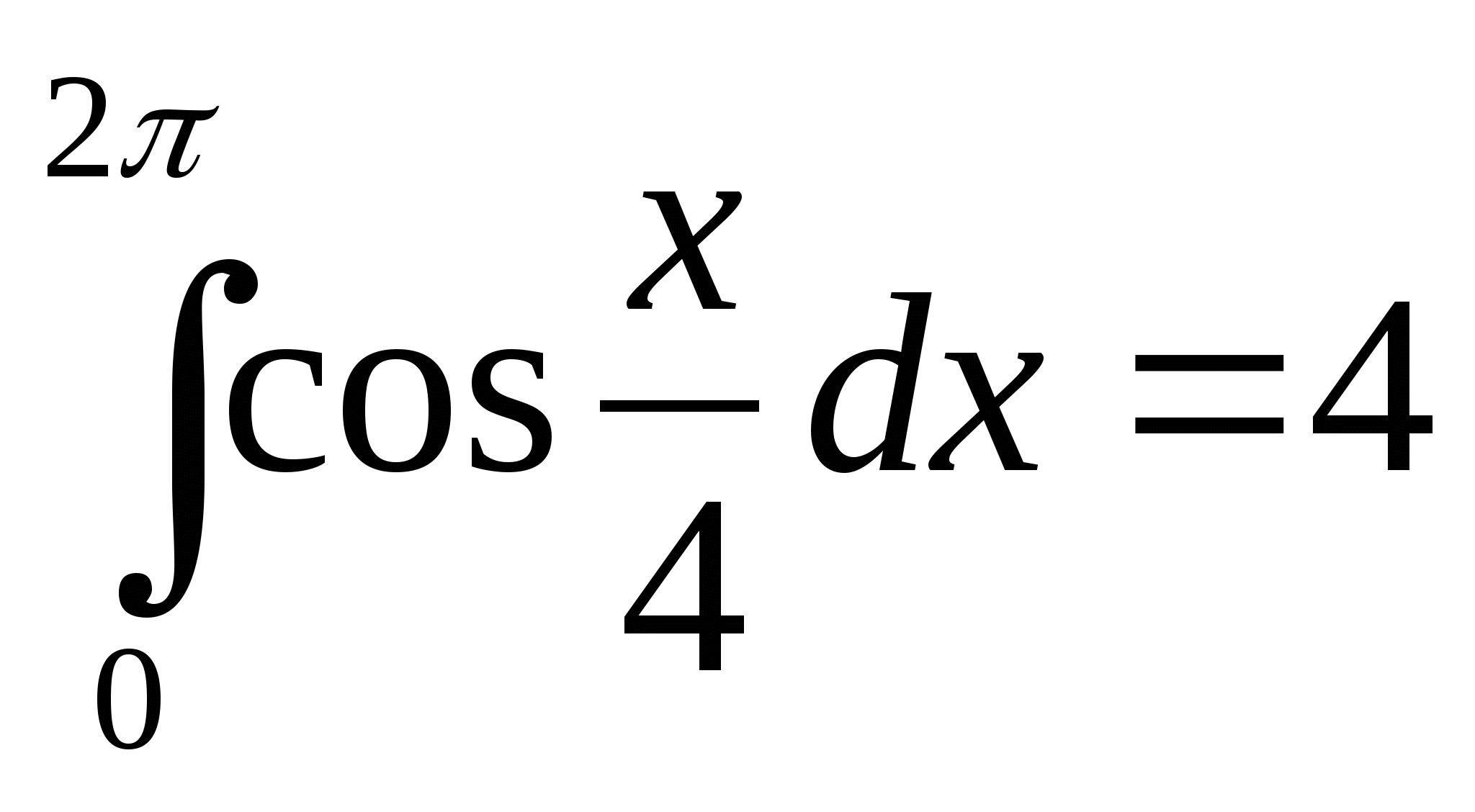 ; 22)
; 22) ![]() ; 23)
; 23) ![]() ; 24)
; 24) ![]()
25) ![]() ; 26)
; 26) 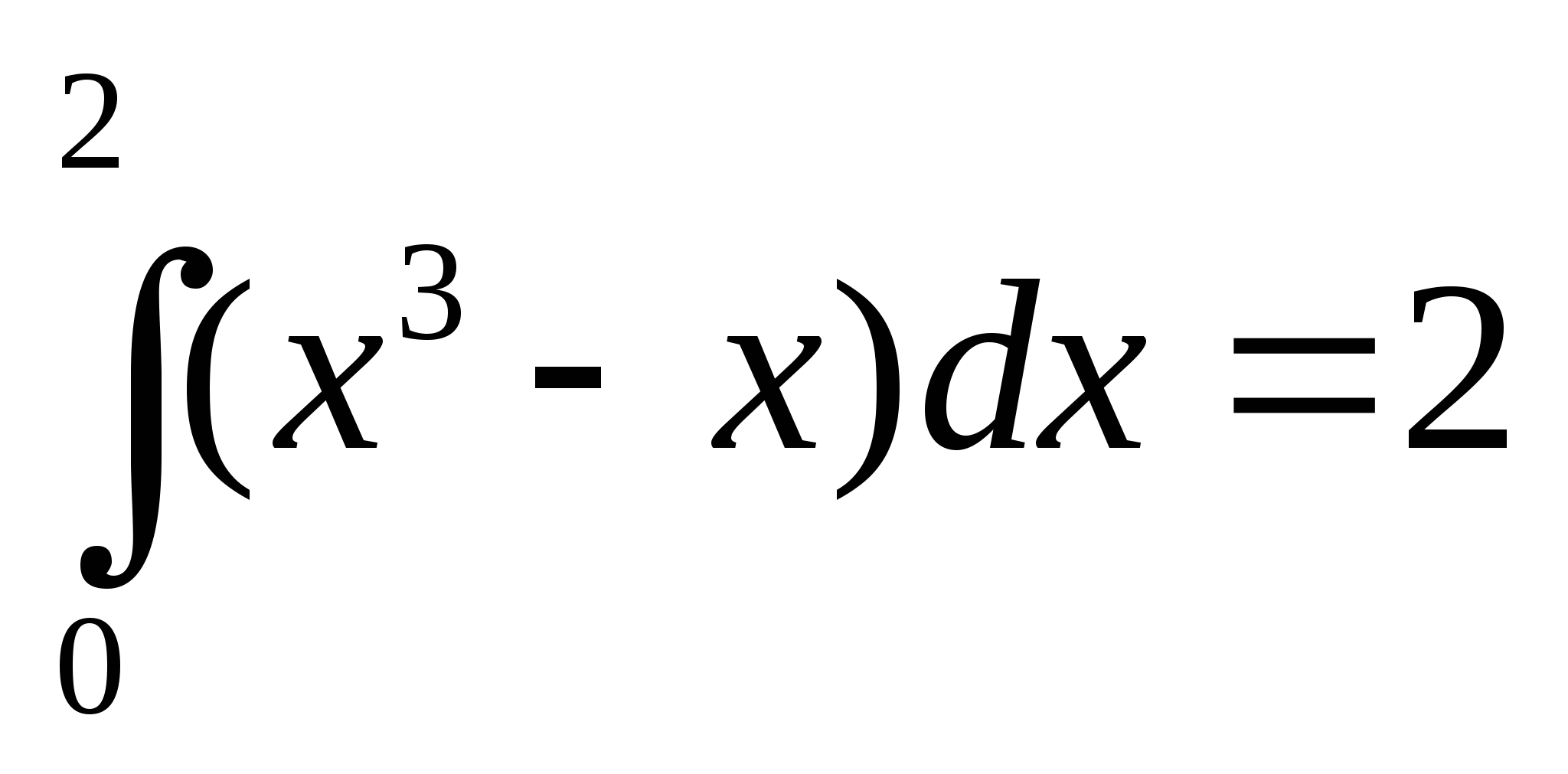 ; 27)
; 27) ![]() ; 28)
; 28) ![]() .
.
Ответы:
![]() - в; 6 - и;
- в; 6 - и;
![]() - я ;
- я ;
2 - з; 6,2 - ж; 18 - е;
0 - т; ![]() - а; 24,2 -
к;
- а; 24,2 -
к;
![]() - д; 9 - ь; 48 -
л;
- д; 9 - ь; 48 -
л;
2 - р; 10,5 - н; 63,75 - ю.
4 - о;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
ж и з н ь и д о в е р и е т е р я ю т
20 21 22 23 24 25 26 27 28
т о л ь к о р а з
Пятый гейм «Гонка за лидером»
Каждая «семья» получает карточку. 1 и 3 «семьи» получают карточку 1, 2 и 4 - карточку 2. В каждой карточке по два задания: одно - в форме теста, другое - своеобразный кроссворд.
За верно решенное 1 задание «семья» получает 1 балл, за 2 задание - 3 балла. Время выполнения задания 20 минут.
Карточка 1
Задание 1.
Для функции f(х)=![]() найти
первообразную, график которой
найти
первообразную, график которой
проходит через точку М(4;5).
А) F(х)=![]() +3; Б)
F(х)=2
+3; Б)
F(х)=2![]() +1; В)
F(х)=2
+1; В)
F(х)=2![]() +3; Г)
F(х)=
+3; Г)
F(х)=![]() +5.
+5.
Ответ: Б
Задание 2
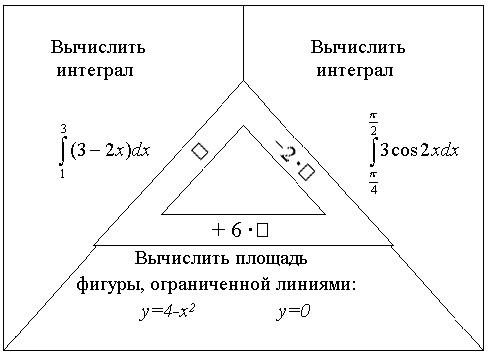
Ответ 65.
Карточка 2
Задание 1
Для функции ![]() найти
первообразную, график которой
найти
первообразную, график которой
проходит через точку М(1;3).
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
Ответ: В.
Задание 2.
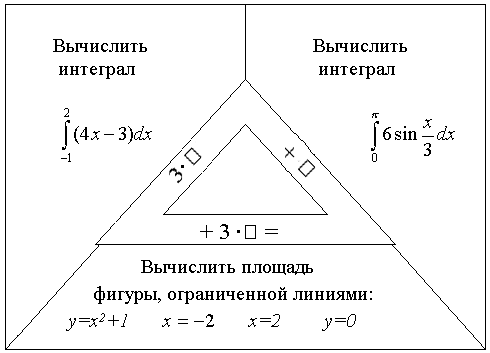
Ответ: 28.
Подведение итогов
На табло подсчитываются баллы, полученные каждой «семьей» и распределяются места. Каждый участник «семьи», занявшей 1 место получает оценку 5. Кроме этого, все учащиеся получают оценку за индивидуальное задание и за работу в коллективе.
Каждая «семья» должна ответить на 3 вопроса:
1. Что вам понравилось в зачете такого рода?
2. Какие цели были достигнуты на этом уроке?
3. Что вам не понравилось и что бы вы изменили?