Исследовательская работа по метематике для 10 класса на тему «Решение тригонометрических уравнений»

Российская Федерация

Ямало-Ненецкий автономный округ

муниципальное образование пуровский район

МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ШКОЛА-ИНТЕРНАТ СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ»

с. САМБУРГ ПУРОВСКОГО РАЙОНА

Исследовательская работа

Автор:

Худи Татьяна, ученица 10б класса

Научный руководитель:

Вовк Ирина Анатольевна,

учитель математики

Самбург, 2012

Содержание

1. Введение..........................................................................................................2

2. Методы решения тригонометрических уравнений………………………..4

2.1. Иррациональные тригонометрические уравнения…………………4

2.2. Решение уравнений понижением степени………………………….6

2.3. Использование ограниченности функции…………………………..8

3. Заключение…………………………………………………………………...9

4. Список литературы ……………….…………………………………………9

5. Приложение…………………………………………………………………10

1. Введение

При изучении тригонометрических уравнений в общеобразовательной школе не хватает времени на рассмотрение уравнений, решаемых нетрадиционными способами. Поэтому мне стало интересно рассмотреть решения таких уравнений, тем более такие уравнения я встречала на олимпиадных заданиях и эти знания мне пригодятся в дальнейшем.

С точки зрения стандартных школьных методов решения тригонометрических уравнений, рассмотрю новые методы, не изучаемые в школьном курсе. Задача называется стандартной, если при ее решении применяется известный алгоритм или ее можно решить по образцу.

Задача называется нестандартной, если при ее решении трудно сказать на какой теоретический материал она опирается, если неизвестно каким способом она решается. В ходе решения таких задач необходимо сначала провести поиск плана решения задачи, определить теоретический материал, который дает ключ к решению задачи. Решать такие задачи интересно и увлекательно. С помощью нестандартных задач можно самостоятельно установить какой-либо математический факт, более глубоко вникнуть в теоретический материал. Решение задач творческого характера помогают развивать математическое мышление, ведь математика - это наука для молодых, она - гимнастика ума.

Многим школьникам изучать математику нелегко. Это напряженная, сложная работа. Для ее выполнения нужны физические и умственные усилия, усилия воли, памяти и воображения. А еще нужно вдохновение! У выдающихся математиков есть немало высказываний о красоте математики.

Александров А.Д.: «В науке и технике, в формулах и тонких экспериментах, в теоретических построениях и машинах есть своя внутренняя красота и поэзия».

Жуковский Н.Е.: « В математике тоже есть своя красота, как в живописи и поэзии».

Поль Дирак: «Общие законы природы, когда они выражены в математической форме, обладают математической красотой в очень высокой степени».

Заинтересовавшись темой решения тригонометрических уравнений, я самостоятельно стала пробовать решать уравнения из сборников по математике повышенной сложности, сборников олимпиадных задач и поняла, что моих знаний не хватает для решения многих типов тригонометрических уравнений. Постараюсь как можно лучше раскрыть нестандартные методы решения тригонометрических уравнений путем приведения решений таких уравнений.

Тема исследования: «Решение тригонометрических уравнений оригинальными способами».

Объект исследования: учебный процесс при изучении темы «Тригонометрические уравнения» в средней школе.

Предмет исследования: организация деятельности учащихся по овладению методами решения тригонометрических уравнений.

Гипотеза: если научиться решать тригонометрические уравнения различными способами, то результаты обучения будут лучше и расходы времени на решение будут минимальными.

Цель исследования: овладеть методами решения тригонометрических уравнений, не рассматриваемых в школьном курсе математики.

Задачи:

1. Изучить учебную, научно-популярную литературу.

2. Выявить, изучить, описать методы решения тригонометрических уравнений.

3. Создать методический и дидактический материалы.

Применяемые методы исследования:

1. эмпирические: изучение литературы; обработка материалов и результатов;

2. теоретические: сравнение; классификация; анализ; обобщение.

Новизна исследования состоит в том, что показана возможность эффективного решения отдельных тригонометрических уравнений. Данная проблема в пределах Самбурга исследовалась впервые.

Этапы исследования:

1. изучение учебной, научно-популярной литературы;

2. сбор и решение нестандартных тригонометрических уравнений;

3. анализ и обобщение результатов исследования, составление рекомендаций, методических и дидактических материалов.

База исследования: муниципальное казенное общеобразовательное учреждение «Школа-интернат среднего (полного) общего образования» с.Самбург, 10б класс (2011-2012 учебный год).

Структура работы: работа состоит из введения, двух глав, заключения, списка литературы и приложения.

2. Методы решений тригонометрических уравнений

Лучше всего организовать работу, посвященную решению нестандартных тригонометрических уравнений, основываясь на решении разнообразных уравнений.

1. Иррациональные тригонометрические уравнения

При решении иррациональных тригонометрических уравнений обычно применяется метод равносильных преобразований. Следует внимательно следить за соблюдением всех сформированных в ходе решения задачи условий, например за соблюдением условия 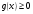при переходе от уравнения 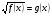к уравнению 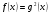. Вместе с тем решать неравенство 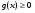не нужно. Надо лишь отобрать среди решений уравнения 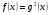те значения , для которых .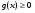

Пример № 1. Решить уравнение .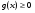

Решение.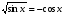

Сделаем в уравнении 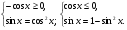замену 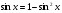и отметим, что 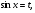Получим 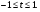Корни этого уравнения: 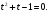и 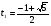. Корень 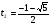посторонний, так как 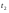. Следовательно, получаем уравнение 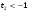. Общая формула его решений: 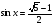Однако здесь общая формула неудобна, её следует разбить на две серии решени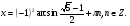й: и 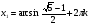Так как должно выполняться неравенство 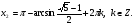, то уравнению удовлетворяет 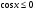и не удовлетворяет .

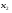Ответ: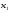

Пример № 2. Решить уравнение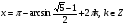

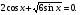
Т.к. 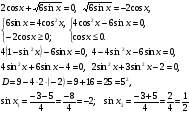то значение - 2 не подходит.

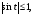
Это решение разобьем на две серии: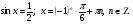

Условию 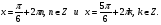удовлетворяет только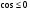

Ответ: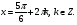

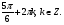
_{Пример № 3. Решите уравнение}

О Д З : (x + 18) cos x  0.

Возведем обе части уравнения в квадрат:

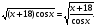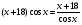, =0.

Решим данное уравнение (cosx  0,см. ОДЗ).

cos² x (x + 18) - (x + 18) = 0,

(cos² x - 1) (x + 18) = 0,

cos x = + 1, cos x = - 1 или x = - 18.

x = 2k, k  Z. x =  + 2m, m  Z.

Произведем отбор корней в соответствии с О Д З.

1) х = -18, (18 + 18) cos 18  0, cos 18  0 (заметим, что угол, выраженный в радианах, принадлежит четвертой четверти, 18  5,7 ).

cos 18  0 - верно.

2) х = 2к, (2k + 18) cos2k  0,

т.к. cos 2k = 1, то

2k  - 18,

2k  - 5,7 ,

k  - 2,85

k = -2,-1, 0, 1,… .

3) х =  + 2m, ( + 2m + 18) cos ( + 2m )  0,

т.к. cos ( + 2m ) = -1, то

 +2m + 18  0,

 +2m  - 18,

2m  - 5,7  - ,

m  -3,35

m = -4, -5 , -6,… .

Ответ: - 18, 2к, к = -2, -1, 0, 1 ,…;  + 2m, m = -4, -5, -6, -7,… .

2.2. Решение тригонометрических уравнений понижением степени

Тригонометрических уравнений очень много и все они решаются различными способами. Довольно часто анализ уравнения показывает, что трудность его решения бывает связана с высокими степенями, с которыми тригонометрические функции входят в уравнение. Отсюда формулируется дополнительная задача понизить степень уравнения. В том случае, если степени четные, то понижение может быть выполнено с помощью формул понижения степени:

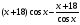
Третью степень можно понизить, опираясь на формулы:

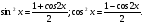
Пример № 1. Решить уравнение sin²x + cos²2x + sin²3x = 1,5.

sin²x + cos²2x + sin²3x = 1,5,

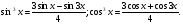
1 - cos2x + 1 + cos4x + 1 - cos6x = 3, (cos2x + cos6x) - cos4x = 0.

Воспользуемся формулой cosx + cosy = 2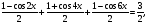coscos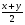

2cos4x cos(-2x) - cos 4x = 0, cos4x (2cos2x - 1) = 0,

cos4x = 0 или 2cos2x - 1 = 0

4x = 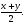cos2x =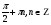

x = 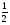2x =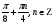

x =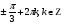

Ответ: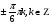

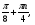
Пример № 2. Решить уравнение sin⁸x - cos⁸x = 0,5cos²2x - 0,5cos2x.

sin⁸x - cos⁸x = 0,5cos²2x - 0,5cos2x,

(sin⁴x - cos⁴x)(sin⁴x + cos⁴x) = 0,5cos2x(cos2x - 1),

(sin²x - cos²x)(sin²x + cos²x)((sin²x)² + 2sin²xcos²x + (cos²x)² - 2sin²xcos²x) = 0,5cos2x(cos2x - 1),

- cos2x ((sin²x + cos²x)² - 2sin²xcos²x) = 0,5 cos2x (- 2 sin²x),

- cos2x (1 - 0,5sin²2x) = - 0,5cos2x 2sin²x,

0,5cos2x sin²2x - cos2x + cos2x sin²x = 0; cos2x (0,5sin²2x - 1 + sin²x) = 0,

cos2x (0,5sin²2x - cos²x) = 0; cos2x (2 sin²x cos²x - cos²x) = 0,

cos2x cos²x (2sin²x - 1) = 0,

cos2x = 0 или cos²x = 0 или 2sin²x = 1

2x = 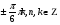х = 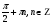sin²x = 0,5

x = 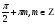sinx = - 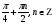или sinx =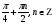

x = (-1)^k+1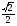 x= (-1)^k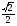

Ответ: 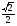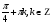(-1)^k+1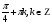(-1)^k.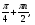

Пример № 3. Решить уравнение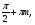

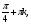
По формулам понижения степени получаем

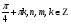
Еще раз применив формулу понижения степени, получим 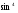, отсюда

; ,

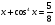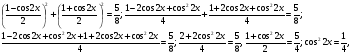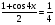
_Ответ: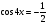

2.3. Использование ограниченности функции

При решении уравнений свойство ограниченности снизу или сверху на некотором множестве часто играет определяющую роль. Например, если для всех х из некоторого множества М справедливы неравенства f(х)>А и g(х)<���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������

���� № 1. Решите уравнение sin(х³+2х²+1)=х²+2х+3.

Для любого действительного числа х имеем sin(х³+2х²+1)≤1, х²+2х+3=(х+1)²+2≥2. Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда больше либо равна двум, то данное уравнение не имеет решений.

Ответ: нет решений.

Пример № 2. Решить уравнение х³ - х - sinпх=0.

Очевидно, что х=0, х=1, х= - 1 являются решениями данного уравнения. Для нахождения других решений уравнения (1) в силу нечетности функции f(х)=х³ - х - sinпх достаточно найти его решения в области х > 0, х ≠ 1, поскольку если х_о > 0 являются его решением, то и (- х_о) также являются его решением.

Разобьем множество х>0, х≠1, на два промежутка: (0;1) и (1;+∞).

Перепишем данное уравнение в виде х³ - х=sinпх. На промежутке (0;1) функция g(х)=х³ - х принимает только отрицательные значения, поскольку х³< х, а функция h(х)= sinпх только положительные значения, значит на этом промежутке уравнение не имеет решений.

Пусть х принадлежит промежутку (1;+∞). Для каждого из таких значений х функция g(х)=х³ - х принимает положительные значения, функция h(х)= sinпх принимает значения разных знаков, причем на промежутке (1;2] функция h(х) = sinпх неположительная, значит на промежутке (1;2] уравнение решений не имеет.

Если же х>2, то │sinпх│≤ 1, х³ - х = х(х² - 1) > 2*3=6, а это означает, что и на промежутке (2;+∞) уравнение (1) также не имеет решений. Итак, х=0, х=1 и х= - 1и только они являются решениями исходного уравнения.

Ответ: - 1, 0,1.

Пример № 3. Решить уравнение х + 5 sin x = x + 5.

Данное уравнение равносильно совокупности систем

x  - 5, или x < -5,

(x+5) sin x = x+5. - (x+5) sin x = x+5.

Решением первой системы является Решением второй системы являются

х = -5, а также корни уравнения корни уравнения sin x = -1

sin x = 1, удовлетворяющие удовлетворяющие условию

условию x  -5,т.е. х < -5, т.е.

sin x = 1, sin x = -1,

x = /2 + 2k, k  Z. x = - /2 + 2m, mZ.

/2 + 2k  -5, полагая - /2 + 2m < -5, полагая

5  5/3 , имеем -5  -5/3, имеем

/2 + 2к  - 5 /3, - /2 + 2m < -5/3,

2к  -5/3 - /2, m < - 7/12, mZ.

к  -13/12, k  Z. m = -1 ,-2, -3,… .

к = -1, 0, 1, … .

Ответ: -5; /2 + 2к, к = -1, 0, 1 ,…; -/2 + 2m,  = -1, -2, -3,….

3.Заключение

Исследование показало, что школьникам нравится та работа, которая пронизана творческими элементами, учение наполняется радостью, когда приходится самостоятельно думать, искать, находить. Учащихся привлекает активная работа мысли, поиск правильного и красивого решения, участие в творческой работе, преодоление трудностей.

Проделав данную исследовательскую работу, я пришла к выводу, что данные методы во многих случаях очень удобны, так как позволяют избежать громоздких преобразований и исключают потерю корней.

Не хочу останавливаться на достигнутом и в будущем планирую изучение других методов решения тригонометрических уравнений.

4.Используемая литература

1. Н.И.Зильберберг «Методы решения тригонометрических уравнений», Псков, 1994 год.

2. А.Н.Коломогоров «Алгебра и начала анализа», Москва, «Просвещение», 2008 год.

3. Вавилов В. В., Мельников И. И., Олехник С. Н.. «Задачи по математике. Уравнения и неравенства».

4. Боревский Л.Я. «тригонометрия». Курс математики для школьников и абитуриентов. - М.; ИНТЭК ЛТД, 1997 - 160 с.

5. Игудисман О. С. «Математика на устном экзамене».

6. Лурье М. В., Александров Б. И. «Задачи на составление уравнений».

7. Олехник С. Н., Потапов М. К., Пасиченко П. И. «Уравнения и неравенства».

8. Потапов М. К., Олехник С.Н., Нестеренко Ю. В. «Математика. Методы решения задач».

9. Смолич Б. А., Ефимов Г. Н., Соловьёв А. Ф. «Уравнительные вычисления».

Приложение

Для самостоятельного решения

Решите уравнения:

1. 2 cos 3x + 4 sin x/2 = 7

2. 3 cos 3x + cos x = 4

3. sin x sin 3x = - 1

4. cos 2x + cos 3 x / 4 - 2 = 0

5. cos²(2x + /3 ) + cos²(/12 - x) = 0

6. cos 6x + sin 5x / 2 = 2

7. х + 3sin x = х + 3

8. x - 6  cos x = x - 6

9. cos²3x + cos⁴4x + cos²5x = 1,5

10. sin²6x + sin²x = 1

11. 6 cos²x + 2 cos²2x = 5.