Контрольная работа № 1 по теме «Числовая окружность»

Контрольная работа № 1 (1 час)

Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.

Вариант 1

1. Задает ли указанное правило функцию

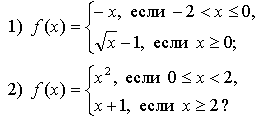
В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках 0, 1, 3, -1;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

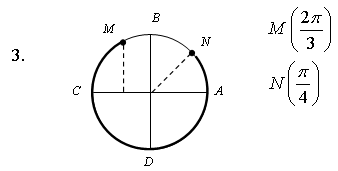
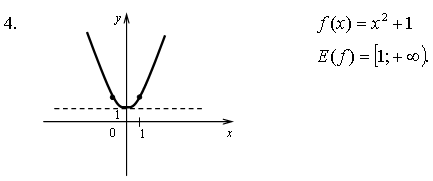
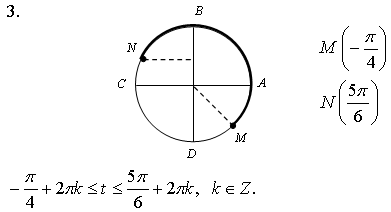
3. На числовой окружности взяты точки 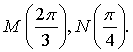Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.

4. Задайте аналитически и постройте график функции у которой

5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция убывает на R. Решите неравенство

Вариант 2

1. Задает ли указанное правило функцию

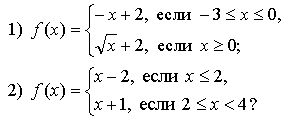
В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках -4, -2, 0, 4;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

3. На числовой окружности взяты точки 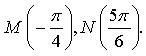Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN. Сделайте чертёж.

4. Задайте аналитически и постройте график функции у которой

5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция возрастает на R. Решите неравенство

Вариант 3

1. Задает ли указанное правило функцию

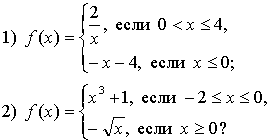
В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках -1, 0, 2, 5;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

3. На числовой окружности взяты точки 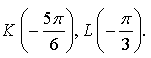Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге KL. Сделайте чертёж.

4. Задайте аналитически и постройте график функции у которой

5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция убывает на R. Решите неравенство

Вариант 4

1. Задает ли указанное правило функцию

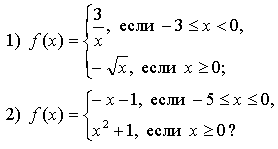
В случае положительного ответа:

а) найдите область определения функции;

б) вычислите значения функции в точках -6, -3, 0, 4;

в) постройте график функции;

г) найдите промежутки монотонности функции.

2. Исследуйте функцию на четность.

3. На числовой окружности взяты точки 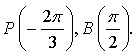Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге PB. Сделайте чертёж.

4. Задайте аналитически и постройте график функции у которой

5. Найдите функцию, обратную функции Постройте на одном чертеже графики этих взаимно обратных функций.

6. Известно, что функция возрастает на R. Решите неравенство

Рекомендации по оцениванию контрольной работы

Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума - до первой черты, задания среднего уровня - между первой и второй чертой, задания уровня выше среднего - после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума - оценка «3»; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) - оценка «4»; за успешное выполнение заданий всех трех уровней - оценка «5». При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).

Решение контрольной работы

Вариант 1

1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.

В случае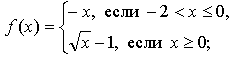

условия не соблюдаются: f(0) = 0 и f(0) = -1.

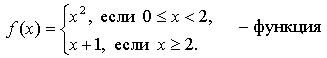
б) - не определено;

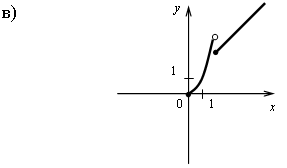
г) на [0; 2) и на [2; +) функция возрастает, в точке х = 2 функция имеет разрыв.

2. - симметрична относительно начала координат.

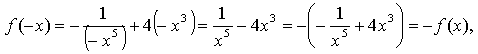значит, функция f(х) - нечетная.

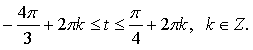
5. у = 2 - х² Квадратичная функция определена и убывает при х  0, значит, существует обратная функция: у = 2 - х²;

Функция

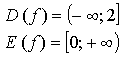
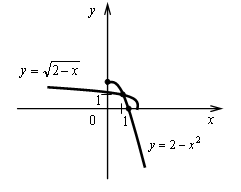
6. у = f(х) убывает на R.

значит, неравенство верно при Возведем обе части в квадрат:

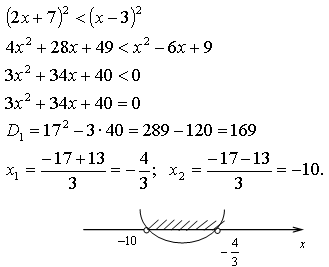
Ответ: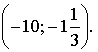

Вариант 2

1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.

В случае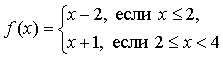

условия не соблюдаются: f(2) = 0 и f(2) = 3.

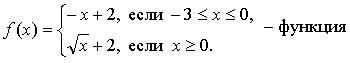
б) f(-4) - не определено;

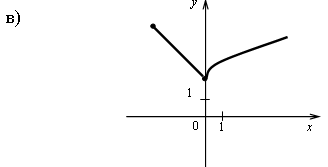
г) на функция убывает; на функция возрастает.

2. - не симметрична относительно начала ординат, значит, функция ни четная, ни нечетная.

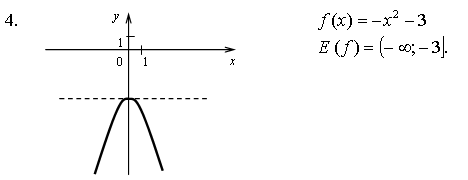
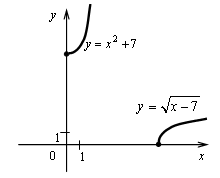
5. у = х² + 7. Квадратичная функция определена и возрастает при х  0, значит, существует обратная функция: у = х² + 7;

Функция

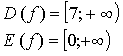
6. f(х) возрастает на R.

значит, неравенство верно при

Возведем обе части в квадрат:

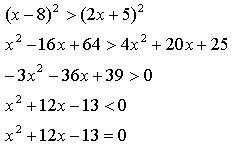
По теореме Виета х₁ = -13; х₂ = 1.

Ответ: (-13; 1).

Вариант 3

1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.

В случае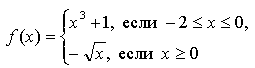

условия не соблюдаются: f(0) = 1 и f(0) = 0.

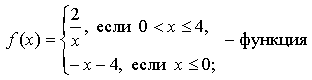
б) - не определено.

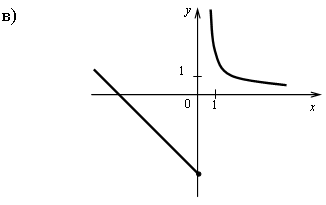
г) на (-; 0] и на (0; 4] функция убывает, в точке х = 0 функция имеет разрыв.

2. - симметрична относительно начала координат.

значит, функция f(х) - четная.

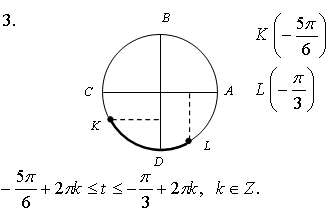
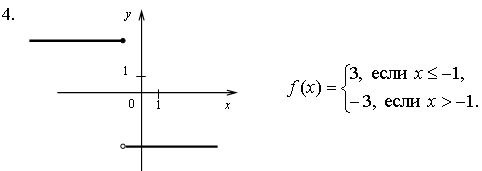
5. Функция определена и возрастает на [2; +∞), значит, существует обратная функция, определенная на [0; +∞):

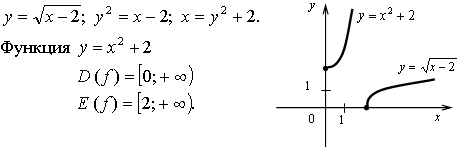
6. у = f(х) убывает на R.

значит, неравенство верно при

Возведем обе части в квадрат:

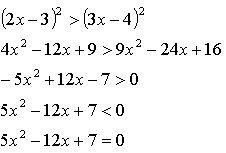
По теореме Виета

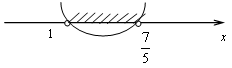
Ответ: (1; 1,4).

Вариант 4

1. Правило задает функцию, если, во-первых, можно выполнить действия, а во-вторых, соблюдается однозначность функции.

В случае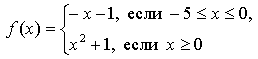

условия не соблюдаются: f(0) = -1 и f(0) = 1.

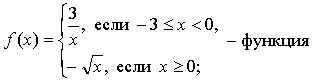
б) f(-6) - не определено;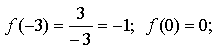

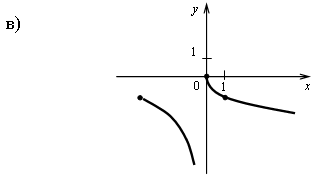
г) на [-3; 0) и на [0; +) функция убывает, в точке х = 0 функция имеет разрыв.

2. - симметрична относительно начала координат.

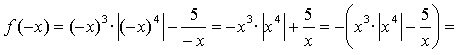-f(х), значит,

функция f(х) - нечетная.

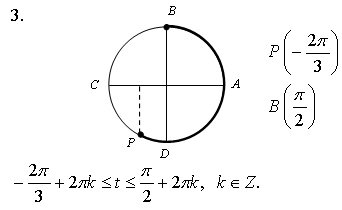
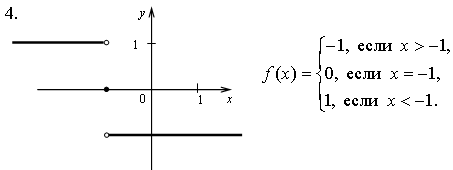
5. Функция определена и возрастает на [-3; +∞), значит, существует обратная функция, определенная на [0; +∞).

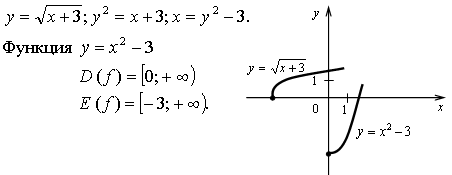
6 у = f(х) возрастает на R.

значит, неравенство верно при

Возведем обе части в квадрат:

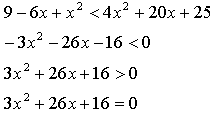
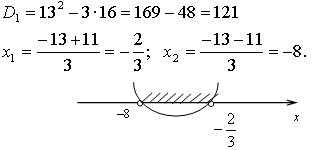
Ответ: