Конспект урока по математике на тему 'Статистические методы обработки информации. Вероятность и геометрия'

Конспект по алгебре и началам анализа.

Учитель: Денисенко Н. В.

Тема: Статистические методы обработки информации. Вероятность и геометрия.

Класс: 11.

Цели:

1. Познакомить учащихся со статистическими методами обработки информации.

2. Обучить составлению и анализу таблиц статистических данных (провести эксперимент).

3. Показать связь теории вероятностей с геометрией.

4. Повторить изученные ранее понятия из теории вероятностей (событие, совместные и несовместные события, классическое определение вероятности).

5. Расширить культуроведческую компетенцию школьников.

6. Научить построению геометрических моделей для нахождения вероятностей и работе с ними.

План:

1. Вступительное слово учителя.

2. Проведение эксперимента, составление статистической таблицы.

3. Анализ полученной статистической таблицы.

4. Работа с многоугольниками распределения и гистограммами.

5. Раскрытие связи между вероятностями и геометрией посредством решения задачи.

6. Самостоятельная работа.

7. Заключительное слово учителя, подведение итогов урока.

8. Домашнее задание.

Оборудование: тетрадь, интерактивная доска, карточки.

Организация: вступительное слово учителя, эксперимент, работа с таблицами и гистограммами, решение задачи, самостоятельная работа по карточкам, заключительные выводы по теме.

Ход урока:

1. Организационный момент.

2. Вступительное слово учителя.

Вы уже имели знакомство с теорией вероятностей в прошлом году. Сегодня мы продолжим знакомиться с этим разделом математики, рассмотрим связь вероятности с геометрией, а также поговорим о статистике.

Знакомясь с теорией вероятностей, мы проводили опыты и измерения, вычисляли вероятности конкретных событий. Но данные большого числа измерений имеют одно неприятное свойство. Оно состоит в том, что информация имеет огромный объем. Например, данные о результатах Единого государственного экзамена в нашем городе. Так вот одна из основных задач статистики состоит в надлежащей обработке информации. Данные упорядочивают и группируют, составляют таблицы распределения, затем графики распределения и, наконец, делают выводы на основании проведенного исследования.

На практике реализация этих шагов проводится с помощью различных компьютерных программ обработки и анализа данных. Существуют специальные статистические программы: «Statistica», «MiniTab» и другие. Но наша цель сегодня - познакомится с тем, что происходит с информацией при ее статистической обработке.

2. Проведение эксперимента, составление статистической таблицы.

Для этого проведем эксперимент. Закройте, пожалуйста, глаза, сосредоточьтесь и загадайте число от 0 до 9. Запишите его в тетрадь, но пока никому не показывайте. Психологи проводили исследования и сделали вывод о том, что о человеке можно судить по тому, какое число он выбирает. Этого, конечно, недостаточно, чтобы судить о человеке, но мнение это довольно популярно.

К доске приглашается ученик, который с первой строке записывает все числа от 0 до 9, а во второй под каждой цифрой - количество человек, загадавших ее. По мере заполнения таблицы можно комментировать каждую цифру следующим образом.

0. - оригинальность.

1. - лидерство.

2. - уравновешенность.

3. - талант и веселость.

4. - устойчивость и прочность.

5. - склонность к риску.

6. - надежность.

7. - таинственность.

8. - материальное благополучие.

9. - успешность.

Первая строка дает нам представление о вариантах, вторая - о кратностях каждой варианты, которые можно записать и в процентах, третьей строкой.

Таблица будет иметь следующий вид.

Варианта

0

1

2

3

4

5

6

7

8

9

Всего вариант:

Кратность

Сумма =

Частота

Сумма =

Частота, %

Сумма = %

3. Анализ полученной статистической таблицы.

Сколько у нас всего вариант?

10

Чему равна сумма всех кратностей?

Она равна единице

Чему равна сумма всех кратностей в процентах?

100%

Какую цифру в вашем классе загадывали чаще всего?

4. Работа с многоугольниками распределения и гистограммами.

По данной статистической таблице данных мы можем составить многоугольник распределения кратностей, если варианту и соответствующую ей кратность возьмем за координаты точки на плоскости.

На интерактивную доску выводятся рисунок.

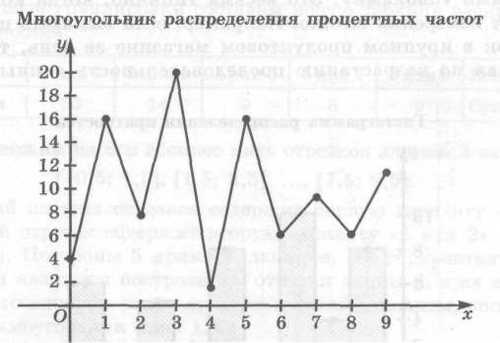
Если же по оси ординат брать значение в десятичных дробях, а не в процентах, мы получим иной многоугольник распределения.

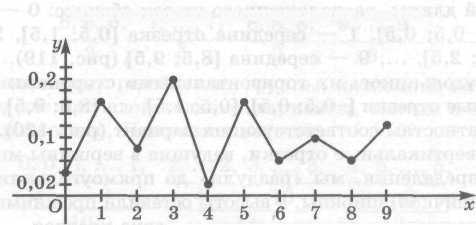
По таким многоугольникам распределения строятся так называемые гистограммы распределения кратностей, примеры которых вы можете видеть на интерактивной доске.

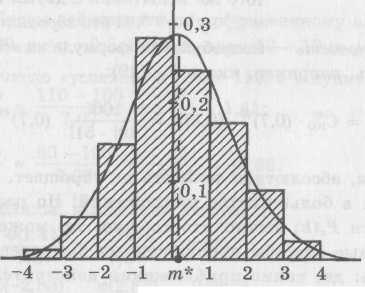
Гистограммы дают четкое представление о каком-либо процессе, по ним удобно анализировать результаты исследования. По этой причине они часто используются в статистике.

5. Раскрытие связи между вероятностями и геометрией посредством решения задачи.

Вы уже знаете классическое определение вероятности события.

Назовите элементы этой формулы.

Она может быть применена только в том случае, если количество испытаний - конечное число. Но как быть, если число опытов - бесконечно? Когда это возможно?

В этом случаи можно воспользоваться связью между теорией вероятностей и геометрий. Тогда для нахождения вероятности используют следующую формулу:

,

где - площадь области, где состоится событие А, площадь всей области, где возможно событие А.

Приведем пример.

Задача о шпионах.

Два шпиона назначили встречу у зоомагазина «Хомячок». Каждый из шпионов может сказать только одно - он появится у назначенного места с 12-00 до 13-00. Но у шпионов существует негласное правило: ждать встречи только 15 минут, после чего уходить. Какова вероятность того, что шпионы встретятся?

Прежде, чем решать подобные задачи, необходимо создать геометрическую модель, и только после этого - работать с ней.

Приступим к первому этапу.

Вводим систему координат и выбираем удобные для данной задачи единицы измерения. Шпионы могут появиться по условию только в течение одного часа. Возьмем один час за единицу измерения.

Дадим шпионам имена.

Пусть приходу первого соответствует ось абсцисс, а времени прихода второго - ось ординат. Тогда что представляет собой точка с координатами ?

Возможное время прихода первого, как и второго, шпиона - в рамках одного часа. Раньше 12-00 они не придут, позже 13-00 - тоже. Тогда квадрат ОАВС на нашем чертеже - область возможного времени прихода шпионов.

Но что означает тот факт, что шпионы не ждут больше 15 минут?

Разность во времени прихода не должна превышать 15 минут. Только в этом случае шпионы встретятся. При этом не важно, кто придет из шпионов первым, а кто вторым.

В нашей системе координат как представляется 15 минут?

Можем записать:

Отсюда получим два неравенства, которые должны выполняться одновременно:

Дадим геометрическую интерпретацию этим неравенствам на чертеже.

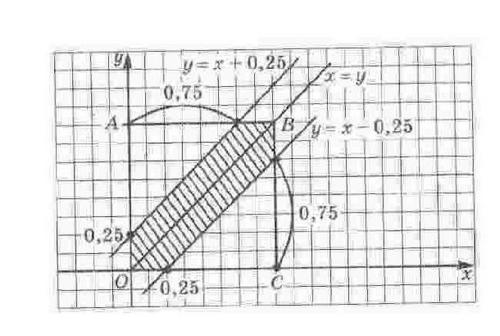
Заштриховав область, которая показывает, в каких случаях встреча состоится, применим формулу геометрической вероятности.

Как найти площадь заштрихованной области?

Из площади квадрата вычесть площади двух равных треугольников.

Получим:

6. Самостоятельная работа.

Два варианта, два задания. На дополнительную оценку дается задание более сложного уровня.

0. вариант.

№ 1.

Заполните таблицу.

Варианта

№1

№2

№3

№4

Всего: 4 варианты

Кратность

5

Сумма =

Частота

0,45

0,1

Сумма =

Частота, %

25

20

Сумма = %

№ 2.

Какова вероятность того, что решения неравенства

будут являться решениями неравенства

0. вариант.

№ 1.

Заполните таблицу.

Варианта

№1

№2

№3

№4

Всего: 4 варианты

Кратность

8

Сумма =

Частота

0,35

0,15

Сумма =

Частота, %

40

10

Сумма = %

№ 2.

Какова вероятность того, что решения неравенства

будут являться решениями неравенства

Дополнительное задание.

Варианта

№1

№2

№3

№4

№5

№6

Всего: 6 вариант

Кратность

291

113

Сумма =

Частота

0,122

0,193

Сумма =

Частота, %

29,1

20,2

7,9

Сумма = %

7. Заключительное слово учителя, подведение итогов урока.

8. Домашнее задание.

Задачник Мордковича: № 22.1 (в, г), № 22.2 (а, б), № 22.12, № 22.21.