- Учителю
- Конспект урока математики в 8 классе на тему 'Рациональные уравнения'
Конспект урока математики в 8 классе на тему 'Рациональные уравнения'
Муниципальное бюджетное образовательное учреждение Новодмитриевская средняя общеобразовательная школа
Методическая разработка
урока математики.
8 класс
«Рациональные уравнения»
Выполнил: учитель математики
1 квалификационной категории
Перова Марина Константиновна
2012 год.
Тема: «Рациональные уравнения»
Класс: 8
Форма проведения: Урок с использованием ИКТ.
Цель: Повторить алгоритм решения рациональных уравнений; рассмотреть решение рациональных уравнений различного уровня сложности, а так же биквадратные уравнения и уравнения, решаемые с помощью замены переменной; развивать умение решать рациональные уравнения.
Задачи:
-
Образовательная.
-
Закрепить вычислительные навыки учащихся при решении рациональных уравнений, в зависимости от дискриминанта.
-
Развивающие.
-
Развивать у учащихся память, внимание, логическое мышление для нахождения корней рационального уравнения при различных видах деятельности на уроке.
-
Работа над развитием математической речи учащихся, направленная на четкое, логическое обоснование своих ответов.
-
-
Воспитательные.
-
Создание на уроке творческой атмосферы и положительного настроя каждого ученика.
-
Воспитывать аккуратность в оформлении письменных заданий.
-
Создание ситуации успеха для детей.
-
План урока.
-
Организационный момент. (1 минута)
-
Актуализация опорных знаний.
-
проверка домашней работы. (5 минут)
-
устная работа. (6минут)
-
Закрепление изученного материала по теме: «Решение рациональных уравнений». Выполнение упражнений при работе в группах. (10 минут)
-
Самостоятельная работа. (14 минут)
-
Домашнее задание. (2 минуты)
-
Заключительный этап урока. (2 минуты)
Конспект урока.
-
Организационный момент.
Деятельность учителя
Деятельность ученика
Урок начинается с названия темы, записанной на доске: «Рациональные уравнения» и сообщение цели урока.
Учащиеся внимательно записывают тему урока в тетрадь и прослушивают цель урока.
-
Актуализация опорных знаний.
-
проверка домашней работы.
-
№ 26.5(а); №26.14(а)
Дополнительное задание по группам.
Смотри приложение.
Учащиеся комментируют свое решение, используя компьютер.
-
устная работа.
Индивидуальная работа у доски 3 учащихся.
Найдите ошибки и исправьте их.
а)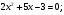
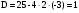 >0
>0
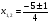
х =
=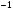 ; х
; х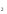 =
=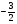 .
.
Ответ: х =
=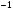 ; х
; х =
=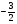 .
.
б)3х²+7х+2=0
 >0
>0
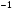
х =2; х
=2; х =
=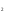 .
.
Ответ: х =2; х
=2; х =
= .
.
в)х²-9х-10=0
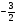 <0.
<0.
Ответ: действительных корней нет
Класс работает устно.
На мониторе записано:
1)Найти дискриминант уравнения:
2х²-3х-14=0
2)Сколько корней имеет уравнение:
х²+10х+25=0
3)Найдите коэффициент «к» для уравнения х²+кх-30=0, если один из корней равен -6.
а) 5; б) -5; в) 1; г) -1.
4)Сформулировать алгоритм решения рациональных уравнений.
Какие из чисел 2;1;3;-4 не могут являться корнями уравнения:
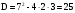
1)D=121.
2) (х+5) ²=0,х=-5.
3)36-6к-30=0,к=1.
Ответ: «в».
4)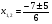 , х
, х =2; х
=2; х =
= .
.
Ответ: 1;3;-4.
III. Закрепление изученного материала по теме: «Решение рациональных уравнений». Выполнение упражнений при работе в группах.
I группа. Найдите сумму корней уравнения:
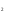
1) 3; 3) -3;
2) 0; 4) 1.
Решите и прокомментируйте решение.
решение:
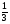 ,
,

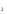 ,
, 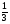
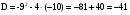 ,
, 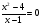
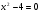

проверка:
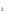
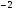
3+0=3
Ответ: (1).
II группа. Укажите промежуток, которому принадлежит сумма корней уравнения:
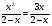
1)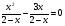 ; 2)
; 2)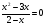 ; 3)
; 3)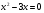 );4)
);4) 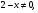 .
.
решение:
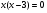 ,
,
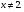 ,
,
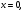 ,
, 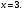
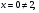
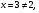 ,
,
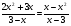 ,
,
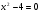
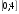
проверка:
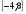
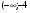
0+(-4)=-4
Ответ: (2).
III группа. а) Найдите координаты точек пересечения графиков функций:
у=5х и у=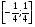 .
.
б) Решите уравнение, используя метод введения новой переменной:
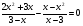
решение:
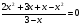
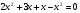
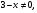
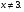
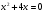
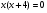
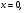
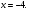
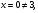
х =2; х
=2; х =
=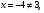 .
.
проверка:
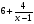
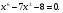
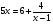
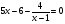
Ответ: (2;10), 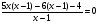
решение: пусть 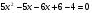 тогда
тогда
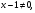 , D=81
, D=81
t =8; t
=8; t =-1
=-1
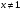
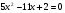
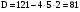
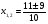
Ответ: х=2; х=-1.
-
Самостоятельная работа.
Каждая группа выполняет тестовое дифференцированное задание. Учитель следит за работой учащихся. Предлагает прокомментировать правильно выполненные задания, используя компьютер.
Выполнение заданий (смотри приложение).
Проверяют выбранные ответы, используя компьютер.
-
Домашнее задание.
I группа 26.2(б ) . 26.15(а)
II группа 26.7(г), 26.16(б)
III группа 26.8(в), 26.22(а)
Задание, аналогичное выполненному на уроке.
Запись в дневнике.
-
Итог урока.
Выставление оценок за работу на уроке, их комментирование.
Выявление заданий, которые вызвали интерес к их выполнению.
Домашнее задание к уроку.
I группа. Решите уравнение:

решение:
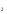
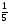
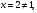
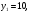
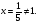
х =0; х
=0; х =2.
=2.
Ответ: х =0; х
=0; х =2.
=2.
II группа. Найдите произведение корней (или корень, если он единственный) уравнения:
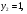
решение:
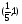
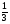
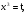
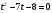

х =2; х
=2; х =
=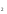 .
.
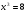 - не удовлетворяет условию
- не удовлетворяет условию 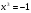
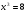 - посторонний корень.
- посторонний корень.
Ответ: х = .
.
III группа. Найдите среднее арифметическое корней уравнения:
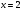
решение:
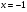
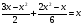
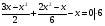
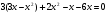
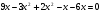
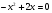
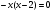


Проверка выполнения условия 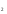
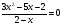
Ответ: 24.
I группа. Найдите сумму корней уравнения:

1) 3; 3) -3;
2) 0; 4) 1.
решение:
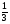 ,
,
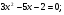
 ,
, 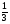
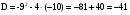 ,
, 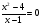
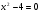

3+0=3
Ответ: (1).
II группа. Укажите промежуток, которому принадлежит сумма корней уравнения:
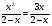
1)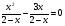 ; 2)
; 2)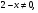 ; 3)
; 3)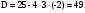 ; 4)
; 4) 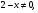 .
.
решение:
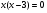 ,
,
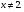 ,
,
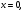 ,
, 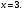
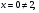
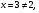 ,
,
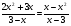 ,
,
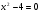
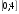
0+(-4)=-4
Ответ: (2).
III группа. 1)Решите уравнение, используя метод введения новой переменной:
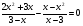
решение: пусть 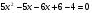 тогда
тогда
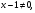 ,
, 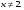
t =8; t
=8; t =-1
=-1
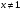
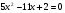
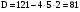
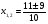
Ответ: 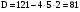 ;
; 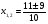 .
.
2)Найдите координаты точек пересечения графиков функций:
у=5х и у=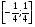 .
.
решение:
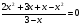 ,
,
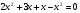 ,
,
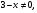 ,
,
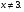 ,
, 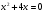
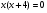
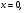 ,
,
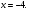
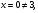
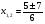

проверка:
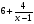
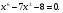
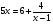
Ответ: 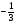
Самостоятельная работа (тест).
I группа.
А1.Какие из чисел 2;5;-3;1 не могут являться корнями уравнения:
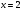
1)2;5;1; 2)-3;1; 3)2;5;-3; 4)5;-3.
А2.Найдите произведение корней (или корень, если он единственный) уравнения:
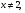
1)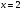 ; 2)
; 2)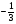 ; 3)
; 3)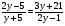 ; 4)
; 4) 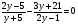 .
.
В1.Решите уравнение:
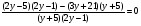
1)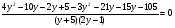 ; 2)
; 2)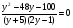 ; 3)
; 3)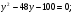 ; 4)
; 4) 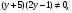 .
.
II группа.
А1.Какие из чисел 2;5;-3;1 не могут являться корнями уравнения:
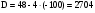
1)2;5; 2)-3;2;5; 3)-3;-1; 4)2;-1;5.
А2.При каком значении переменной «а» уравнение 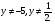 имеет 1 корень.
имеет 1 корень.
1)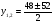 ; 2)
; 2)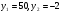 ; 3)
; 3)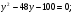 ; 4)
; 4) 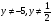 .
.
В1.Решите уравнение:
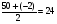
III группа.
А1.Какие из чисел 2;5;-3;1 не могут являться корнями уравнения:
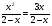
1) 5;-3; 2)2; 3)-3;2;5;1; 4)-3;1.
А2.Решите уравнение:
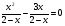
1)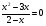 ; 2)
; 2)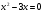 ; 3)
; 3)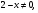 ; 4)
; 4) 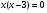 .
.
В1.Решите уравнение:
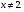
Самостоятельная работа (тест).
I группа.
А1 (3),
А2 (2),
В1 (1).
II группа.
А1 (2),
А2 (1),
В1 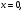
решение:
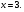
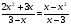
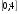
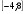

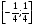
Ответ: 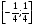
III группа.
А1 (3),
А2 (2),
В1 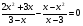
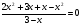
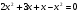
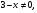
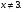
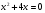
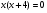
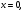
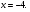
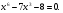
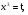
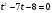
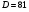

Ответ: -4;1;-2;-1.
Технические средства: мультимедийный проектор
Дидактические материалы:
-карточки для работы в группах;
-карточки для самостоятельной работы;
-презентации для самопроверки и самокоррекции (домашнее задание, самостоятельная работа).
Используемая литература:
-
Учебник : Алгебра 8 кл. А.Г.Мордкович.
-
Т.А.Иванова Современный урок математики. Н. Новгород. 2010г.
-
Контрольно-измерительные материалы. Составитель: Л.Ю.Бабушкина. 2011г.
Интернет ресурсы:
- festival. 1september.ru
фестиваль педагогических идей «открытый урок» («первое сентября»)
- www. problems.ru
база данных задач по всем темам школьной математики.