- Учителю
- Конспект урока по геометрии по теме «Сумма углов треугольника» (7 класс)
Конспект урока по геометрии по теме «Сумма углов треугольника» (7 класс)
Тема урока: «Сумма углов треугольника»
Тип урока: урок повторения, комплексного применения знаний, умений и навыков.
Цель урока:
-
осмысление изученного материала, воспроизведение и применение знаний с целью их углубления;
-
развитие наблюдательности, логического мышления;
-
формирование общих трудовых умений;
Оборудование:
1) карточки-задания "Закончи предложение";
2) карточки для устного счета.
План урока:
1. Организационный момент
2. Актуализация опорных знаний
3. Устное решение задач по готовым чертежам
4. Повторение теории
5. Самостоятельная работа
6. Домашнее задание
7. Итоги урока
Каждому ученику хочется знать оценку своего труда на уроке, причем сразу, после окончания урока.
Чтобы активизировать учащихся, оценить работу каждого, за верный ответ выдаю жетоны - один или два в зависимости от сложности вопроса. 1 жетон оценивается в 1 балл.
У каждого ученика имеется конверт, в который складываются жетоны и небольшие самостоятельные работы, с подсчитанным количеством баллов за работу.
На доске записывается сколько баллов нужно набрать, чтобы получить "5", "4" или "3" за работу на уроке.
В конце урока конверты сдаются учителю.
На доске: 10 б и более - "5"
8 - 9 б - "4"
6 - 7 б - "3"
Ход урока
-
Организационный момент
Сегодня на уроке мы будем применять теоретические знания к решению задач. Решение задач - практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь.
"Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их", - говорил выдающийся математик Д.Пойа.
II. Актуализация опорных знаний
Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию.
Трое учащихся на доске показывают различные способы решения задачи по заранее подготовленным рисункам.
Дано: ΔАВС, АВ=ВС, ВD - биссектриса угла СВК
Доказать: ВD || АС.
Доказательство:
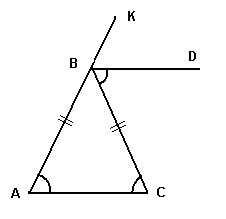
I способ
-
т.к.
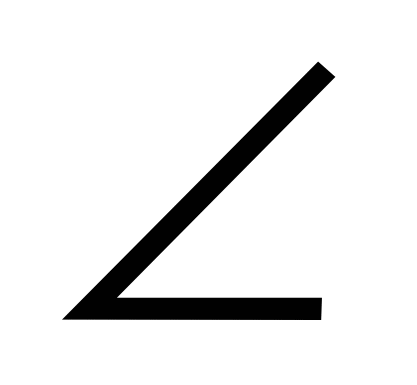 KBC - внешний,
KBC - внешний,
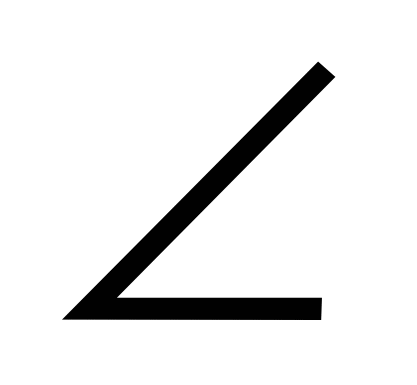 KBC=
KBC=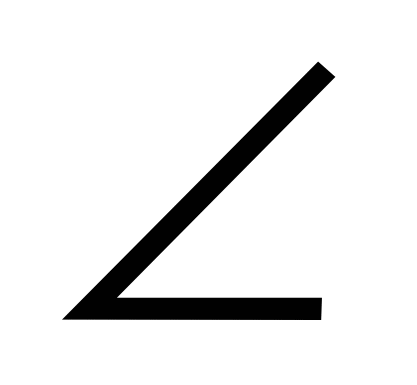 А +
А + 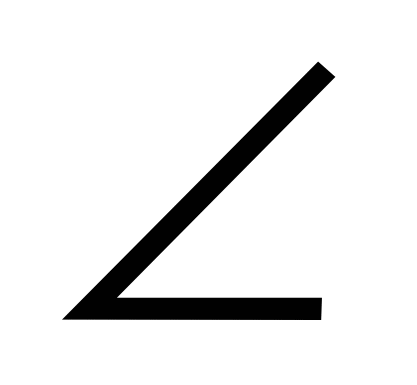 С
С
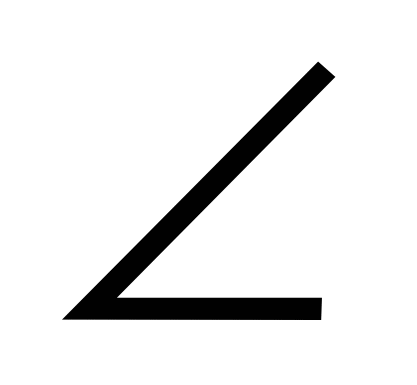 KBC= 2
KBC= 2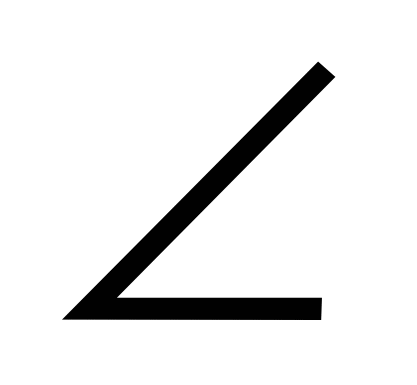 С
С -
т.к. ВD - биссектриса
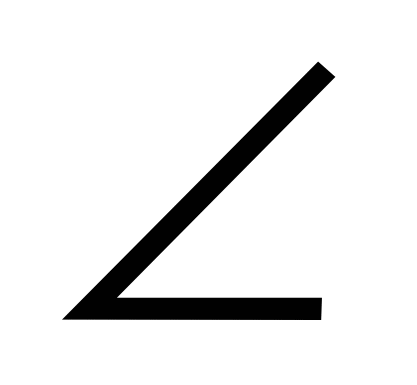 KBD=
KBD=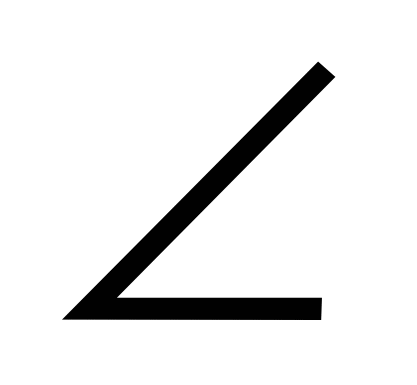 DBC =
DBC =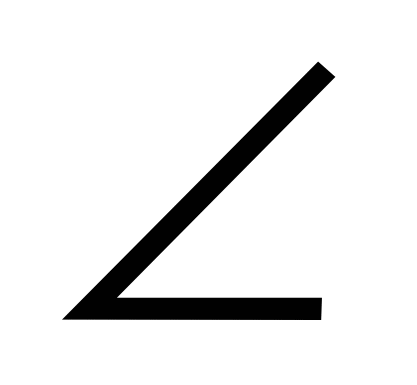 С
С
3) ![]() DBC=
DBC=![]() АСВ значит,
АСВ значит,
BD||АС, ч.т.д.
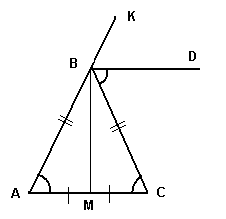
II способ
Построим биссектрису ВМ.
Она является медианой и высотой Δ АВС.
![]() СВК и
СВК и ![]() CВА - смежные,
CВА - смежные,
ВL и ВМ - биссектрисы смежных углов, значит, ВМ![]() BD. Но ВМ
BD. Но ВМ![]() АС, поэтому BD||АС
АС, поэтому BD||АС
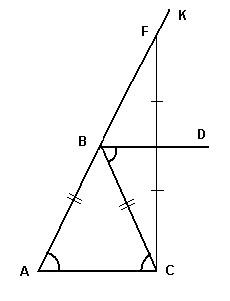
III способ
Отложим BF = AB.
ΔСBF равнобедренный. BD - его биссектриса, медиана и высота, значит, FD = DC.
Рассмотрим ΔAFC.
BD - средняя линия. Значит BD||AC.
III. Устное решение задач по готовым чертежам
В геометрии очень важно уметь смотреть и видеть, замечать и отличать различные особенности геометрических фигур.
К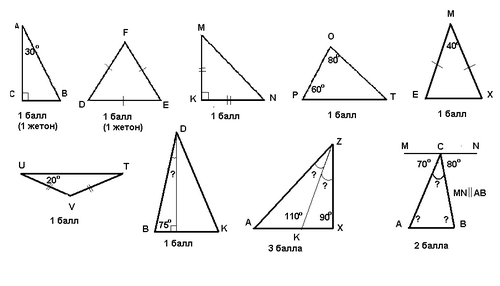 то ничего не замечает,
то ничего не замечает,
Тот ничего не изучает,
Кто ничего не изучает,
Тот вечно хнычет и скучает.
-
Внимательно посмотрите на рисунки и вычислите неизвестные углы треугольника (Рисунки предъявляются классу по одному, каждый рисунок на слайде презентации).
-
Сформулируйте теорему, которую применяли, решая предложенные задачи.
Ребята, которые заинтересовались доказательством этой теоремы, нашли различные способы доказательства. У доски двое доказывают теорему по рисункам, приготовленным дома.
Дано:Δ ABC
Доказать: ![]() А +
А + ![]() В +
В +![]() С = 180о
С = 180о
Доказательство:
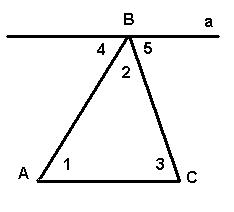
I способ (по учебнику)
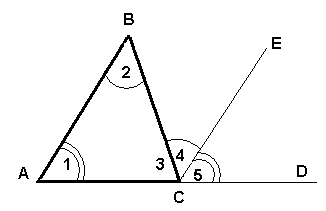
II способ
Строим CE||AB
![]() 2 =
2 =![]() 4 как накрест лежащие
4 как накрест лежащие ![]() 1=
1=![]() 5 как соответственные
5 как соответственные ![]() 3 +
3 +![]() 4 +
4 + ![]() 5=180о
5=180о
![]() 3 +
3 + ![]() 2 +
2 + ![]() 1 = 180о
1 = 180о
Теорема доказана
IV. Повторение теории
Закончи предложение …
Вариант 1
-
Сумма углов треугольника равна …
-
Если углы равнобедренного треугольника при основании равны по 50о, то угол между боковыми сторонами равен…
-
Углы равностороннего треугольника равны по…
-
Внешним углом треугольника при данной вершине называется…
-
Сумма внешнего и внутреннего углов треугольника при данной вершине равна…
-
В ΔКМА внешним является угол…
-
Если два внешних угла ΔАВС равны 100о и 140о, то третий внешний угол равен…
Вариант 2.
-
Сумма углов треугольника равна …
-
Если в ΔАВС
 А = 35о,
А = 35о, 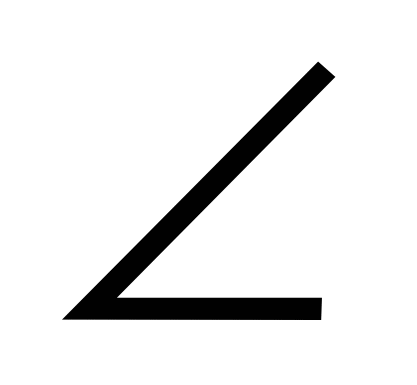 B = 55о, то
B = 55о, то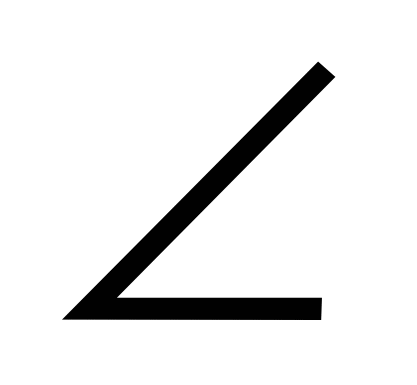 С =…
С =… -
Если угол между боковыми сторонами равнобедренного треугольника равен 100о, то углы при основании равны по…
-
Если сумма двух углов треугольника равна третьему углу, то этот треугольник … (вид треугольника).
-
При данной вершине можно построить … внешних углов.
-
Внешний угол треугольника равен…
-
В ΔКМА внешний
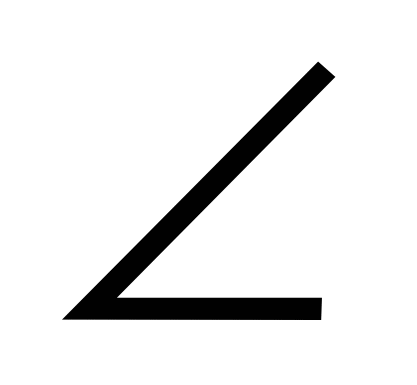 МАС равен …
МАС равен …
После выполнения работы учащиеся меняются карточками. Проговариваются ответы. Верно выполненные задания отмечаются знаком "+", оцениваются в 1 балл. Подсчитывается сумма баллов, жетоны складываются в конверт.
Подсчитывается общее количество баллов в конверте.
V. Самостоятельная работа в тетрадях
ВАРИАНТ 1
ВАРИАНТ 2
1. По данным рисунка определите угол А треугольника АВС.
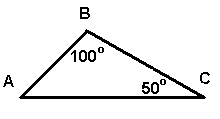
1 б
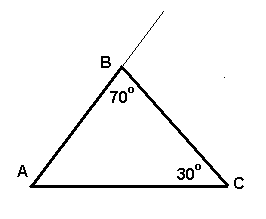
2. В треугольнике КОМ определите величину внешнего угла при вершине М
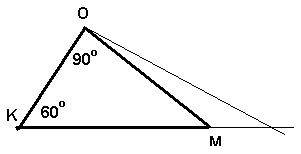
2 б
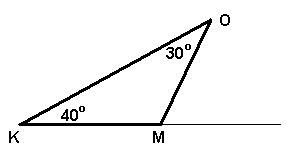
3. В равнобедренном прямоугольном треугольнике ABC (![]() B = 90о) проведена высота BD. Найдите углы треугольника АВD.
B = 90о) проведена высота BD. Найдите углы треугольника АВD.
3 б
3. В равностороннем треугольнике ABC проведена высота BD. Найдите углы треугольника АВD.
4. Известно, что BD - медиана треугольника АВС, ΔDAB - равносторонний. Определите углы треугольника CDB.
4 б
4. На основании AC равнобедренного треугольника ABC отмечены точки D и F так что AD = CF. Определите углы треугольника DBF, если ![]() BFС = 110о
BFС = 110о
После того, как работы будут сданы, ребята могут посмотреть решение на отворотах доски (слайдах презентации) и сравнить со своим.
VI. Домашнее задание
П.30, 31; № 234, индивидуально № 235
VII. Итоги урока
Ответить на вопросы:
-
Сформулируйте теорему о сумме углов треугольника.
-
Какой треугольник называется остроугольным? Тупоугольным? Прямоугольным?
-
Какой угол называется внешним углом треугольника?
-
Каким свойством обладает внешний угол треугольника?
Учащиеся получают две оценки:
За конверт: 10 б и более - "5"
8 - 9 б - "4"
6 - 7 б - "3"
За самостоятельную работу:
10 б и более - "5"
8 - 9 б - "4"
6 - 7 б - "3"