- Учителю
- Теорема Пифагора. Урок геометрии 8 класс.
Теорема Пифагора. Урок геометрии 8 класс.
ТЕОРЕМА ПИФАГОРА
(урок изучения нового материала)
Гроголь Н. В., учитель математики
Линник О. П., учитель математики, информатики
КГУ «Средняя общеобразовательная школа-лицей №38»
г. Семей, ул.Пржевальского, 16а, тел.:537337, licey38@mail.ru
Цель урока: познакомить учащихся с теоремой Пифагора, научить применять ее к решению геометрических задач.
Задачи урока.
Образовательные:
1. Познакомить учащихся с теоремой Пифагора и ее доказательством.
2. Решить ряд задач с использованием теоремы Пифагора.
3. Познакомить учащихся с основными этапами жизни и деятельности Пифагора.
4. Повторить зависимость между сторонами прямоугольного треугольника.
Воспитательные:
1.Формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: критичность мышления, интуиция, логическое мышление.
2. Воспитывать ответственность и добросовестное отношение к учебному труду.
Развивающие:
1.Развивать приемы мыслительной деятельности: анализ, синтез, сравнение, обобщение, классификация.
2. Существенно расширить круг геометрических задач, решаемых школьниками.
3.Повышение любознательности, стремление к использованию приобретенного на уроке опыта в реальной жизни, за рамками учебного процесса.
Оборудование: ПК, проектор, интерактивная доска, флипчарты «Теорема Пифагора», раздаточный материал (тест).
Предварительная подготовка: подготовить учащихся, которые выступят с докладом о жизни Пифагора Самосского.
План урока
-
Организационный момент.
-
Актуализация знаний.
-
Сообщение учащихся о жизни Пифагора Самосского.
-
Доказательство теоремы.
-
Решение задач с помощью теоремы Пифагора.
-
Проверочный тест.
-
Решение занимательных задач с помощью теоремы Пифагора.
-
Подведение итогов урока.
-
Домашнее задание.
Ход урока
Учитель. Здравствуйте, ребята! Тема нашего сегодняшнего урока «Теорема Пифагора». Цель нашего урока: познакомиться с теоремой и научиться применять ее для решения геометрических задач. Но прежде мы повторим пройденный материал, который пригодится нам на сегодняшнем уроке.
-
Какие тригонометрические выражения вы знаете?
-
Дать определение косинуса, синуса, тангенса, котангенса острого угла в прямоугольном треугольнике. (устно)
-
Решение устных задач на нахождение тригонометрических выражений. (флипчарты)
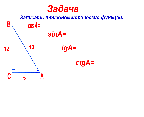
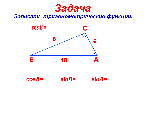
Сегодня на уроке мы приступаем к изучению одной из важнейших теорем геометрии - теоремы Пифагора. И эпиграфом к сегодняшнему уроку подойдут следующие слова Иоганна Кеплера (флипчарт): "Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень".
Эти слова очень точно определяют значимость данной теоремы - она сравнима с мерой золота.
Но сначала послушаем рассказ о математике, именем которого она названа. Сообщение подготовили (называются учащиеся).
Как вы услышали Пифагор сделал много важных открытий, но наибольшую славу ученому принесла доказанная им теорема, которая сейчас носит его имя.
Откройте тетради, запишите число и тему урока - «Теорема Пифагора».
- Ребята, может быть, вы что-нибудь слышали о теореме Пифагора? (Пифагоровы штаны во все стороны равны).
Действительно, это шуточная формулировка теоремы.
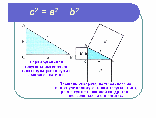 В современных учебниках теорема формулируется так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
В современных учебниках теорема формулируется так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- Как записать теорему Пифагора для прямоугольного треугольника АВС с катетами a, b и гипотенузой с. (флипчарт)
Предполагают, что во времена Пифагора теорема звучала по-другому: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах»
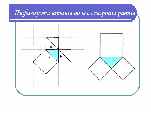
А вот и «Пифагоровы штаны во все стороны равны», вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. (флипчарт)
А вот такие шаржи придумывались учащимися средних веков при изучении теоремы. (флипчарт)
Прежде чем мы перейдем к доказательству теоремы, хотелось бы сказать, что насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей. Глубина этой древней истины, по-видимому, далеко не исчерпана. (флипчарт)
Докажем теорему Пифагора. (флипчарты)
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

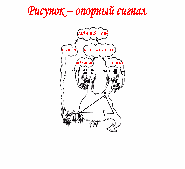 Приближается зачет по геометрии, а на зачетах и экзаменах иногда бывают случаи, когда ученики, вытянув билет или получив вопрос, помнят формулировку теоремы, но забывают с чего начать доказательство. Чтобы этого не произошло с вами, предлагаю рисунок - опорный сигнал (флипчарт). Думаю, он надолго останется в вашей памяти. «Отрубил Иван-царевич дракону голову, а у него две новые выросли» На математическом языке это означает: провели в треугольнике АВС высоту СD, и образовалось два новых прямоугольных треугольника - ADC и BDC. Вспомнив рисунок, вы вспомните дополнительное построение и начало доказательства теоремы.
Приближается зачет по геометрии, а на зачетах и экзаменах иногда бывают случаи, когда ученики, вытянув билет или получив вопрос, помнят формулировку теоремы, но забывают с чего начать доказательство. Чтобы этого не произошло с вами, предлагаю рисунок - опорный сигнал (флипчарт). Думаю, он надолго останется в вашей памяти. «Отрубил Иван-царевич дракону голову, а у него две новые выросли» На математическом языке это означает: провели в треугольнике АВС высоту СD, и образовалось два новых прямоугольных треугольника - ADC и BDC. Вспомнив рисунок, вы вспомните дополнительное построение и начало доказательства теоремы.
Теорема Пифагора - одна из главных теорем геометрии, потому что с ее помощью можно доказать много других теорем и решить множество задач.
Решим устно несколько задач по готовым чертежам (флипчарты).

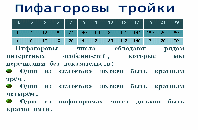
Получили прямоугольный треугольник со сторонами 3,4 и 5ед. Это единственный прямоугольный треугольник, стороны которого равны трем последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен еще древним египтянам. Кроме этих чисел существует целый ряд, так называемых пифагоровых троек. (флипчарт).
Эти числа обладают рядом свойств, которые мы перечислим без доказательств. (см. флипчарт).
А теперь письменно решим следующую задачу. (флипчарт с готовым чертежом)
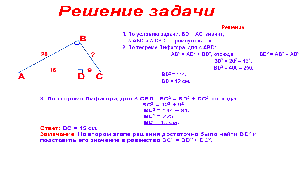
Сегодня на уроке мы познакомились с одной из главных теорем геометрии - теоремой Пифагора и ее доказательством. И для проверки усвоения ваших знаний сейчас предлагаю вам написать проверочный тест.
По результатам теста вам будет выставлена оценка за урок.
Тест по геометрии
Теорема Пифагора, 8 класс
1 вариант
1. Что называется косинусом острого угла в прямоугольном треугольнике?
А) отношение прилежащего катета к гипотенузе;
Б) отношение противолежащего катета к гипотенузе;
В) отношение противолежащего катета к прилежащему катету;
Г) отношение прилежащего катета к противолежащему катету.
2. Что называется тангенсом острого угла в прямоугольном треугольнике?
А) отношение прилежащего катета к гипотенузе;
Б) отношение противолежащего катета к гипотенузе;
В) отношение противолежащего катета к прилежащему катету;
Г) отношение прилежащего катета к противолежащему катету.
3. Отношение противолежащего катета к гипотенузе - это …
А) косинус острого угла в прямоугольном треугольнике;
Б) синус острого угла в прямоугольном треугольнике;
В) тангенс острого угла в прямоугольном треугольнике;
Г) котангенс острого угла в прямоугольном треугольнике.
4. Отношение прилежащего катета к противолежащему катету - это …
А) косинус острого угла в прямоугольном треугольнике;
Б) синус острого угла в прямоугольном треугольнике;
В) тангенс острого угла в прямоугольном треугольнике;
Г) котангенс острого угла в прямоугольном треугольнике.
5. Дан прямоугольный треугольник АВС. Определить cosА (рис.1)
А
С
В
29
21
20
Рис.1
А) 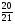 ; Б)
; Б) 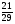 ; В)
; В) 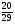 ; Г)
; Г) 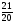 .
.
6. Дан прямоугольный треугольник АВС. Определить sinА (рис.1)
А) 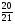 ; Б)
; Б) 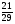 ; В)
; В) 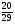 ; Г)
; Г) 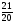 .
.
7. Дан прямоугольный треугольник АВС. Определить tgА (рис.1)
А) 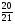 ; Б)
; Б) 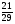 ; В)
; В) 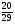 ; Г)
; Г) 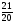 .
.
8. Дан прямоугольный треугольник АВС. Определить ctgА (рис.1)
А) 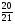 ; Б)
; Б) 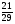 ; В)
; В) 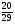 ; Г)
; Г) 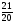 .
.
M
K
10
6
N
Рис.2
9. Дан прямоугольный треугольник MNK (рис.2). Найти NK.
А) 8;
Б) 7;
В) 12;
Г) 11.
10. Дан прямоугольный треугольник MNK (рис.2). Найти sinN.
А) 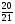 ; Б)
; Б) 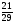 ; В)
; В) 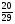 ; Г)
; Г) 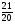 .
.
Тест по геометрии
Теорема Пифагора, 8 класс
2 вариант
1. Что называется синусом острого угла в прямоугольном треугольнике?
А) отношение прилежащего катета к гипотенузе;
Б) отношение противолежащего катета к гипотенузе;
В) отношение противолежащего катета к прилежащему катету;
Г) отношение прилежащего катета к противолежащему катету.
2. Что называется котангенсом острого угла в прямоугольном треугольнике?
А) отношение прилежащего катета к гипотенузе;
Б) отношение противолежащего катета к гипотенузе;
В) отношение противолежащего катета к прилежащему катету;
Г) отношение прилежащего катета к противолежащему катету.
3. Отношение прилежащего катета к гипотенузе - это …
А) косинус острого угла в прямоугольном треугольнике;
Б) синус острого угла в прямоугольном треугольнике;
В) тангенс острого угла в прямоугольном треугольнике;
Г) котангенс острого угла в прямоугольном треугольнике.
4. Отношение противолежащего катета к прилежащему катету - это …
А) косинус острого угла в прямоугольном треугольнике;
Б) синус острого угла в прямоугольном треугольнике;
В) тангенс острого угла в прямоугольном треугольнике;
Г) котангенс острого угла в прямоугольном треугольнике.
5. Дан прямоугольный треугольник АВС. Определить cosB (рис.1)
А
С
В
10
8
6
Рис.1
А) 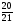 ; Б)
; Б) 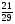 ; В)
; В) 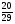 ; Г)
; Г) 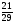 .
.
6. Дан прямоугольный треугольник АВС. Определить sinB (рис.1)
А) 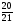 ; Б)
; Б) 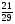 ; В)
; В) 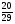 ; Г)
; Г) 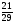 .
.
7. Дан прямоугольный треугольник АВС. Определить tgB (рис.1)
А) 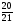 ; Б)
; Б) 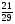 ; В)
; В) 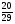 ; Г)
; Г) 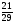 .
.
8. Дан прямоугольный треугольник АВС. Определить ctgB (рис.1)
А) 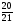 ; Б)
; Б) 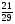 ; В)
; В) 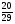 ; Г)
; Г) 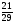 .
.
M
K
5
3
N
Рис.2
9. Дан прямоугольный треугольник MNK (рис.2). Найти NK.
А) 4;
Б) 6;
В) 8;
Г) 10.
10. Дан прямоугольный треугольник MNK (рис.2). Найти cosМ.
А) 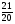 ; Б)
; Б) 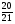 ; В)
; В) 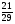 ; Г)
; Г) 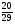 .
.
После написания теста, предлагаю решить занимательные задачи. (флипчарты)
Подведение итогов.
Итак, сегодня на уроке мы познакомились с одной из главных теорем геометрии - теоремой Пифагора и ее доказательством. Давайте вспомним формулировку теоремы.
Запишите домашнее задание: стр. 41-44, №141, 143.