- Учителю
- Урок по теме «Решение тестовых заданий по тригонометрии», 10 класс
Урок по теме «Решение тестовых заданий по тригонометрии», 10 класс
Костенко Галина Алексеевна,
учитель математики СШ №1,
г. Петропавловск, Казахстан
10 класс
Тема: «Приемы работы с тестовыми заданиями по тригонометрии»
Цели: - обобщить и систематизировать знания учащихся на применение формул тригонометрии:
- формирование навыков решения тестовых заданий.
Задачи:
Образовательные:
- формировать умения применять тригонометрические формулы при упрощении и вычислении тригонометрических выражений;
- формировать навыки решения тестовых заданий с использованием различных приемов.
Развивающие:
- совершенствовать практические навыки учащихся, умения анализировать результаты своей практической деятельности, проводить анализ ответов в тестах;
- способствовать развитию творческой, мыслительной активности учащихся, логического мышления, умению применять знания в нестандартных ситуациях.
Воспитательные:
- развивать самостоятельность при решении тестовых заданий, способность к самоконтролю и самооценки результатов своей деятельности:
- развивать у учащихся коммуникативные компетентности (культуру общения, умение работать в коллективе).
Оборудование: ПК учителя, интерактивная доска, карточки для индивидуальной работы.
Мультимедийные компоненты:
- презентация, содержащая материал для проведения урока;
- ActivInspire флипчарт
Ход урока
-
Актуализация знаний.
а) проверка домашнего задания.
Разобрать из домашнего задания пример 1.
Вычислить: ![]() .
.
Решение.
Используем формулу понижения степени, получим
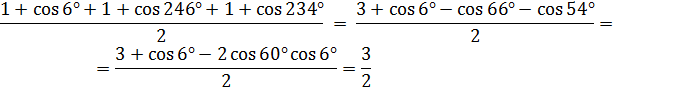
б) По карточкам работают 3 человека ( задания на соответствия проверяются на интерактивной доске).
Карточка 1. Вычислить: ![]()
Ответ: ![]() .
.
Карточка 2. Установите соответствие между тождественно равными выражениями:
-
1. tgx.cosx
-
А) sinx
-
2.
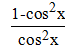
В)![]()
-
3. (1- sin2x)(1+sin2x)
С) 1
-
4.
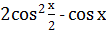
D) 2
-
5. tgx(ctgx + tgx)
Е) sin22x
F) tg2x
-
cos22x
Правильный ответ: 1 - А, 2 - F, 3 - G, 4 - C, 5 - B.
Карточка 3. Известно, что ![]() . Установите соответствие между тригонометрической функцией того же аргумента и её значением.
. Установите соответствие между тригонометрической функцией того же аргумента и её значением.
-
соs
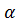
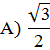
-
2. tg
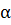
![]()
-
3. sin(-2
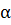 )
)
С) ![]()
-
4.
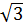
D) - ![]()
-
5.
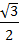 -1
-1
Е) 2
F) - ![]()
G) 1
Правильный ответ: 1 - В, 2 - С, 3 - D, 4 - А, 5 - F .
Пока учащиеся работают по карточкам, проводится устная работа с классом.
(слайд 2-4 )
а) Дано: tg![]() =
= ![]() , 0 <
, 0 <![]() < 900. Вычислить: а) sin
< 900. Вычислить: а) sin![]() ; б) cos
; б) cos![]() ; в) 2sin
; в) 2sin![]() + 3cos
+ 3cos![]() .
.
Решение. 3, 4, 5 - египетский треугольник, следовательно, sin![]() =
= ![]() , cos
, cos![]() ,
,
2sin![]() + 3cos
+ 3cos![]() =
= ![]() .
.
б) Вычислить sin![]() , если cos
, если cos![]() ,
, ![]() 3 четверти.
3 четверти.
Ответы: А) ![]() В)
В) ![]() С)
С) ![]() D) -
D) - ![]() Е)
Е) ![]() .
.
Обратить внимание учащихся, что sin![]() в 3 четверти имеет знак «-», сл-но, ответ D).
в 3 четверти имеет знак «-», сл-но, ответ D).
в) Вычислить: 1) ![]() , если cos
, если cos![]()
![]() ,
, ![]() 1 четверти.
1 четверти.
Решение. ![]() 0, тогда 5 - 2 - 1 = 2
0, тогда 5 - 2 - 1 = 2
2) ![]() , если sin
, если sin![]() = 0,5,
= 0,5, ![]() 2 четверти.
2 четверти.
Решение. ![]() 0, тогда
0, тогда ![]() .
.
После устной работы проверить задания по карточкам 2 и 3 на соответствие на интерактивной доске.
-
Использование нестандартных приемов при упрощении и вычислении тригонометрических выражений.
Задание 1.
Дано: cos![]() = -
= - ![]() ,
, ![]() 2 четверти. Найти sin (300+
2 четверти. Найти sin (300+![]() ).
).
Решение. 1 способ. Используем формулу синус суммы двух углов.
2 способ. Так как ![]() 2 четверти и cos
2 четверти и cos![]() = -
= - ![]() , то
, то ![]() =1500, тогда
=1500, тогда
sin1800 = 0.
Задание 2.
Учащимся предлагается слайд с заданиями одного типа. Найти различные способы решения данных заданий.
1) ![]() .
.
2) ![]() .
.
3) ![]() 1.
1.
Во всех этих заданиях следует обратить внимание на то, что степень каждого слагаемого одна и та же. Можно рассмотреть несколько способов решения данного задания:
- поделив каждое слагаемое на cos![]() или sin
или sin![]() и вычислить значение;
и вычислить значение;
- из данного условия выразить cos![]() или sin
или sin![]() и подставить в данное выражение;
и подставить в данное выражение;
А можно используя тождество ![]() вместо sin
вместо sin![]() подставить 3, а вместо cos
подставить 3, а вместо cos![]() подставить 5. Тогда получим: 1) - 4, 2)
подставить 5. Тогда получим: 1) - 4, 2) ![]() , 3) 8.
, 3) 8.
Задание 3.
Упростить выражения:
а) 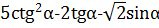
Ответы: А)![]() В) -1 С)1 D) -
В) -1 С)1 D) - ![]() E)
E) ![]() .
.
Решение. Пусть ![]() = 270 (можно 870). Тогда получим:
= 270 (можно 870). Тогда получим: ![]() .
.
б) ![]()
Ответы: А)![]() В) -1 С)1 D) -
В) -1 С)1 D) - ![]() E)
E) ![]() .
.
Решение.
Пусть ![]() =
= ![]() ,
, ![]() . Тогда,
. Тогда, ![]()
в) ![]()
Ответы: А) 2sin![]() B) cos2
B) cos2![]() C) 0.5 cos
C) 0.5 cos![]() D) tg
D) tg![]() E) sin
E) sin![]() .
.
Решение.
1 способ.
![]() =
= ![]()
![]() .
.
![]() .
.
Пусть ![]() =
= ![]() . Получим
. Получим ![]() .
.
Теперь значение ![]() подставляем в ответы. Только вариант А) удовлетворяет условию.
подставляем в ответы. Только вариант А) удовлетворяет условию.
г) ![]() .
.
Ответы: А) 2sin![]() B) cos2
B) cos2![]() C) 0.5 cos
C) 0.5 cos![]() D) tg
D) tg![]() E) 2соs
E) 2соs![]() .
.
Решение.
Пусть ![]() = 0 , тогда
= 0 , тогда ![]() .
.
Подставляя данный угол в ответы, выясняем, что верный ответ Е).
-
Проверка знаний учащихся (тестовые задания).
1 вариант
-
Вычислить tg
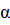 + sin
+ sin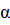 , если cos
, если cos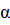 = -
= -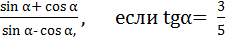 ,
, 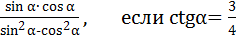 <
< 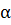 <
<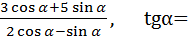 .
.
А)![]() В)
В) ![]() С)
С) ![]() D) -
D) - ![]() E)
E) ![]() .
.
-
Вычислить
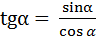 , если ctg
, если ctg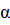 = 1,
= 1, 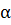 1 четверти.
1 четверти.
А)![]() В)
В) ![]() С)
С) ![]() D) 3 E)
D) 3 E) ![]() .
.
-
Найти значение выражения:
 , если tgx = 2.
, если tgx = 2.
А)![]() В)
В) ![]() С)
С) ![]() D) 7,5 E)
D) 7,5 E) ![]() .
.
-
Упростите выражение:
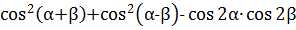 .
.
А)![]() В)
В) ![]() С)
С) ![]() D) -10 E)
D) -10 E) ![]() .
.
-
Упростите выражение:
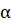 .
.
А)![]() В) tg2
В) tg2![]() С)
С) ![]() -1 D) 2cos2
-1 D) 2cos2![]() E) -cos2
E) -cos2![]() .
.
2 вариант
-
Вычислить tg
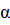 - ctg
- ctg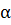 , если sin
, если sin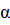 = -
= -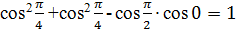 ,
, 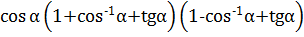 <
< 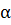 <
<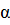 .
.
А)![]() В)
В) ![]() С) -
С) -![]() D)
D) ![]() E)
E) ![]() .
.
-
Вычислить
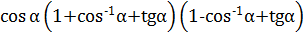 , если sin
, если sin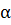 =
= 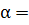 ,
, 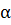 1 четверти.
1 четверти.
А)![]() В)
В) ![]() С)
С) ![]() D) 9 E)
D) 9 E) ![]() .
.
-
Найти значение выражения:
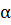 , если ctgx =
, если ctgx = 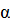 .
.
А)![]() В)
В) ![]() С)
С) ![]() D) 4 E)
D) 4 E) ![]() .
.
-
Упростите выражение:
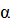 .
.
А) - 2cos2![]() В)
В) ![]() С)
С) ![]() D)
D)![]() E) 2cos2
E) 2cos2![]() .
.
-
Упростите выражение:
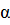 .
.
А)![]() В) 0 С) -1 D) 2 E) -2.
В) 0 С) -1 D) 2 E) -2.
Ответы к тесту.
1
2
3
4
5
1 вариант
А
D
С
Е
В
2 вариант
С
D
В
В
А
-
Домашнее задание:
1) Повторить решение тригонометрических уравнений и неравенств;
-
В тестах найти 10 заданий по тригонометрии с использованием приемов рассмотренных на уроке.