- Учителю
- «Решение дробно-рациональных уравнений» 9 класс
«Решение дробно-рациональных уравнений» 9 класс
«Решение дробно-рациональных уравнений»
Урок: алгебра 9 класс
Тема: Решение дробных рациональных уравнений
Цель: познакомить с новым видом уравнений - дробными рациональными уравнениями, дать представление об алгоритме решения дробных рациональных уравнений.
Задачи:
Образовательные
-
Формирование умения и навыков решения дробных рациональных уравнений.
-
Применение ЗУН упрощения рациональных выражений.
-
Контроль уровня усвоения знаний и умений решения уравнений, приведения подобных слагаемых, приведения к общему знаменателю, вычислительных навыков.
Развивающие
-
Развитие умений выделять главное, существенное в изученном материале.
-
Формирование умений сравнивать, классифицировать, обобщать факты и понятия.
-
Формировать умение пользоваться алгоритмом.
-
Развитие у учащихся самостоятельности в мышлении и в учебной деятельности.
-
Развитие у учащихся познавательного интереса, внимания, математической зоркости.
Воспитательные
-
Содействовать формированию мировоззренческих понятий.
-
Воспитывать чувство коллективизма, сопереживания за группу, товарища.
Оборудование: 1) Карточки с домашним заданием
2) Карточки с заданиями
3) Карточки «проверь себя».
4) Карточки помощницы.
5) Тексты разноуровневой самостоятельной работы.
6) Карточки с дополнительными заданиями.
7)Оценочные карточки.
8)Рефлексия
Структура урока:
-
Актуализация опорных знаний
-
Постановка темы и целей урока
-
Изучение нового материала
-
Закрепление пройденного материала
-
Итог урока
Силу уму придают упражнения а не покой, А. Поп(анг.поэт)
1.Организационный момент (2 мин)
Сегодня на уроке мне хотелось бы вас пригласить поглубже заглянуть в замечательный мир математики - в мир уравнений, в мир поиска, в мир исследований.
Но для начала давайте вспомним, а что такое уравнение? (Равенство, содержащее неизвестное).
- А что значит решить уравнение? (Значит найти все его корни или доказать, что их нет).
- А что является корнем уравнения? (Значение переменной, при котором уравнение обращается в верное равенство).
- Какие виды уравнений, вы знаете и умеете решать? (Линейные, квадратные, дробно-рациональные).
Все способы решений, известных вам уравнений, можно образно представить в виде "ключей". Символ урока - связка ключей - "Линейные уравнения", "Квадратные уравнения", "Дробно-рациональные уравнения", "
2. Проверка домашнего задания(3мин),взимопроверка)
НОМЕР ЗАДАНИЯ
Ответы
1. 0,5 х 2 +0,7 =0
нет корней.
2. (х-5) (х+3)= 9
х1 = - 4 , х2 = 6.
3. (х-5) (х +3)=1 - 2х
х 1= 4, х 2 = - 4.
4. (х-5) (х +3) = 3 (х-5)
х=0, х=5.
5. 2 (х-1) - 1 = 3 - (1-2х)
нет корней
6.1 - 2х + 4х 2 = х 2 -2х + 1
х = 0.
7. 3 (1 - х) + 2 = 5 - 3х
х - любое число.
8. 2х 2 + 3х +4 =0
нет корней
9. х 2 +6х +4 = 0
х 1 = - 3 ± √ 5.
10. 25х 2 - 30х + 9 = 0
х 1,2 = 0,6
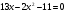 3.: Определите вид каждого уравнения (3 мин)
3.: Определите вид каждого уравнения (3 мин)
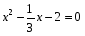
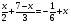
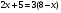
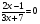
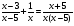
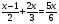
4,Целепологание индивидуально. Тема урока
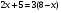
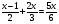 5. Решить уравнения: (2 мин)
5. Решить уравнения: (2 мин)
6.Алгоритм решения уравнений линейных уравнений:
.а)Раскрыть скобки.
б). Перенести слагаемые с переменной в одну сторону, а числа в другую.
В).Найти корень уравнения. предварительно приведя слагаемые.
7.Историческая справка
Первым, кто описал решение линейных уравнений, был Мухаммед аль-Хорезми, написавший трактат «Ал-джебра (перенос слагаемых) и ал-мукабала (приведение подобных слагаемых)»
Для чего нужно уметь решать различные уравнения?
Уравнения оказывают помощь и в других науках, химии, (линейное уравнение)-по основному свойству пропорции.
3.Работа над квадратным уравнением( 5 МИНУТ)
1.х2-7х+12=0
2. 5х2-11х=6-0
3. 2х2-7х=0
Алгоритм решения квадратного уравнения
Физ-пауза 1 МИН
Звучит музыка (саксофон) - 1минута.
А знаете ли вы, что английский математик Д.Сильвестр называл музыку математикой чувств, а математику - музыкой раЗУМА 4.Работа над дробно-рациональным уравнением.
Ход урока
Вводная беседа учителя (2 мин.)
Один начинающий волшебник, герой шуточной песенки, неумело обращался с заклинаниями, в результате вместо грозы у него получилась коза, а вместо утюга - слон. Чтобы решать уравнения, нужно совершать ряд преобразований, и делать это следует очень осмотрительно.
Например, решая уравнения, мы могли бы рассуждать так: 5 МИНУТ
Пример 1
Пример 2
х(х+3) =2х,
х+3 = 2,
х = - 1.
Ответ: х= -1
х 2 +х-1 = 4х-3 ,
х-1 х-1
х 2 +х-1=4х-3,
х 2 -3х+2=0,
х=1 или х=-2.
Ответ: х=1, х= - 2
На самом деле, стараясь избавиться от всего лишнего, мы допустили бы ошибки. Какие?
- В результате неравносильных преобразований в уравнении 1 потерян корень х = 0, а в примере 2 появился «посторонний» корень х = 1.
- Как же не попасть в подобную ловушку?
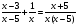
Прежде всего, надо четко знать, какие действия нужно выполнить в ходе решения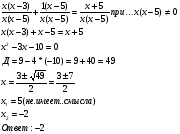
-
Алгоритм решения дробных рациональных уравнений: 2 МИНУТЫ
1 способ.
2 способ.
-
Найти общий знаменатель дробей, входящих в уравнение.
-
Найти допустимые значения дробей, входящих в уравнение.
-
Умножить обе части уравнения на общий знаменатель.
2. Найти общий знаменатель дробей,
входящих в уравнение.
-
Решить получившееся уравнение.
3.Умножить обе части уравнения
на общий знаменатель.
-
Исключить проверкой из корней уравнений те, которые обращают в нуль общий знаменатель.
4. Решить получившееся уравнение.
-
Исключить корни, не входящие в допустимые значения дробей уравнения.
Найди ошибку
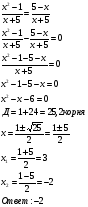
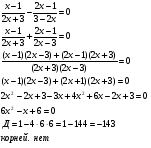
Решение уравнений. 3 МИН
-
Взаимопроверка - 4 варианта. Работа выполняется на листочках. Ответы записаны на обратной стороне доски. В ходе выполнения работы учащиеся определяют для себя алгоритм решения дробных рациональных уравнений. На каждой парте - таблица - напоминание «Алгоритм решения дробных рациональных уравнений». Приложение 1. 5 МИНУТ
Решить самостоятельно
В а р и а н т 1.
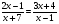
В а р и а н т 2.
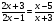
В а р и а н т 3.
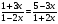
В а р и а н т 4.
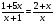
О т в е т ы: на доску с обратной стороны
I вариант: 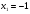 ,
, 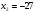 (
(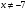 ;
; 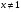 ).
).
II вариант: 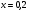 (
(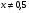 ;
; 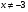 )
)
III вариант: 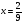 (
(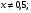
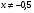 )
)
IV вариант: 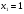 ,
, 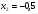 (
(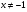 ;
; 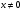 ).
).
5. План исследования уравнения: 2 МИН
-
Провести анализ уравнения.
-
Составить план решения.
-
Реализовать план решения.
-
Составить анализ метода решения и систематизировать опыт.
6.Подведение итогов
VI. Итог урока. (2 мин)
- Чем занимались сегодня на уроке?
- А зачем нужно уметь решать уравнения?
С помощью уравнений можно найти любое неизвестной, решать задачи. Этим мы и будем заниматься на следующих уроках
- А теперь вернемся на начало урока. Каждый из вас для себя поставил цель.
Достигли ли вы этих целей?
Домашнее задание
VII. Выставление оценок. (1 мин)
VIII. Рефлексия. (1 мин) Раздать учащимся карточки
Рефлексивный алгоритм
-
Доволен ли ты тем, как прошел урок?
-
Было ли тебе интересно?
-
Сумел ли ты получить новые знания?
-
Ты был активен на уроке?
-
Ты с удовольствием будешь выполнять домашнее задание?
-
Учитель был внимателен к тебе?
-
Ты сумел показать свои знания?
Оценочный лист учащегося
Фамилия _________________
Имя ______________________
Вид задания
«5»
«4»
«3»
«2»
Домашнее задание
9-10
7-8
5-6
1-4
Этапы
Задания
Количество баллов
1
Домашнее задание
2
Линейное уравнение
3
Квадратное уравнение
4
Дробно-рациональное уравнение
5
Найди ошибку
6
Самостоятельная работа
Итоговое количество баллов
Оценка
ПОДУМАТЬ!!!!!
Задача на совместную работу
-
Двое рабочих выполнили работу за 12 дней. За сколько дней может выполнить работу каждый рабочий, если одному из них для выполнения всей работы потребуется на 10 дней больше, чем другому? Ученик у доски комментирует.
В этой задаче описывается процесс работы двух рабочих отдельно и вместе, который характеризуется величинами: производительность, сроки, работа. Составлю таблицу и заполню ее по тексту задачи.
Производительность (раб/день)
Сроки (дни)
Работа
1 рабочий
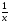
Х
1 (А)
2 рабочий
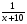
Х + 10
1 (А)
Вместе
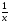 +
+ 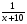 =
= 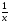
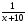
12
1 (А)
Обычно, когда не определен конкретно объем выполняемой работы, то его без ограничения общности, принимают за 1. Решу уравнение:
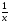 +
+ 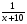 =
= 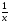
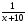 Умножу обе части на 12х(х+10). ОДЗ: х≠0; х≠-10
Умножу обе части на 12х(х+10). ОДЗ: х≠0; х≠-10
12(х+10) + 12х = Х (х+10)
х2 - 14х - 120 = 0
по теоремам Виета
х1 = -6 не удовлетворяет смыслу задачи
х2 = 20 удовлетворяет ОДЗ
Соотнесу полученный результат с вопросом задачи.
Ответ: первому понадобится 20, а второму 30 дней чтобы выполнить эту работу самостоятельно.