Признаки и свойства параллельных прямых(7 класс)

Тема «Признаки и свойства параллельных прямых».

(урок решения задач по данной теме).

Цели урока:

• закрепить знания по теме «Признаки и свойства параллельных прямых»:

• выработать умения применять теоретический материал при решении задач;

• развивать логическое мышление, способности самостоятельно решать учебные задачи.

Оборудование: 2 магнитные доски, таблицы с готовыми чертежами, раздаточный материал.

Ход урока:

1. Ознакомление с темой урока, постановка его целей (2мин)

2. Актуализация опорных знаний учащихся (5 мин)

3. Систематизация знаний и умений по пройденному материалу с использованием упражнений на готовых чертежах (8мин)

4. Решение задач (15 мин)

5. Постановка домашнего задания (2мин)

6. Проверочная работа (12мин)

7. Подведение итогов урока (3мин)

8. Резервные задания.

1) Организационный момент.

2) Актуализация опорных знаний учащихся.

Математика стала наукой лишь с появлением в ней доказательств. Напомню, что под теоремой в математике понимают любое математическое утверждение, справедливость которого устанавливается с помощью доказательства. Математическое доказательство проводится по четко определенным правилам: исходя из ранее известных фактов и теорем в соответствии с законами логики. В математике многие теоремы «ходят парами». Очень часто встречаются пары, состоящие из прямой и обратной теорем. Такую пару образуют, например, теоремы о признаках и свойствах параллельных прямых.

Сформулируйте эти теоремы.

Ответ учащихся:

• Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

• Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

• Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

• Если две параллельные прямые пересечены секущей, то соответственные углы равны.

• Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ , то прямые параллельны.

• Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰ .

Класс работает по таблице. В это же время 6 учеников работают по карточкам с индивидуальным заданием.

Работа с классом.

Решите задачу и укажите, каким свойством или признаком вы пользовались.

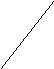
a 1 2

4 3

b 5

c

Дано:

Параллельны ли прямые a и b

m 3

2

n 1

c

Дано:

Найти:,

c

a

x y

b 80⁰

Дано:

Найти:,

c

a

b

Параллельны ли прямые a и b

m n

c 1 2 3

Дано:

Найти:,

D C

O

A B

Дано:

DO=OB

AO=OC

Параллельны ли прямые AB и DC

Ответы учащихся.

1) так как вертикальные углы. . Прямые a и b параллельны. Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ , то прямые параллельны.

2) соответственные углы при пересечении параллельных прямых m и n секущей с. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

односторонние углы при пересечении параллельных прямых m и n секущей с. . Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰ .

3) накрест лежащие углы. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. односторонние углы. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰ .

4) Углы и односторонние углы при пересечении прямых a и b секущей с. . Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ , то прямые параллельны. Прямые a и b параллельны.

5) - соответственные углы при пересечении прямых m и n секущей с Если две параллельные прямые пересечены секущей, то соответственные углы равны.

-смежные углы.

6) Рассмотрим треугольники DOC и AOB.DO=OB , AO=OC , -так как вертикальные углы. Треугольник DOC равен треугольнику AOBпо двум сторонам и углу меду ними. Из равенства треугольников - накрест лежащие углы при пересечении прямых DC и AB секущей DB. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Индивидуальная работа.

Карточка №1 c

1. На рисунке a 1 2

Параллельны прямые a и b? 4 3

Найти все остальные углы.

b 5 6

8 7

2. Точка O середина отрезков AB и CD, докажите, что ADIIBC.

Ответ:

1) Дано: ,

Параллельны ли прямые a и b.

Решение.

- смежные углы.

-соответственные углы при пересечении прямых a и b секущей с. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Значит прямые a и b параллельны. -вертикальные углы.

-вертикальные углы. -накрест лежащие углы. -накрест лежащие углы. -соответственные углы.

Ответ: ,.

2) Дано: AO=OB, CO=OD

Доказать: ADIIBC

A

D

O

C

B

Рассмотрим треугольники AOD и COB. AO=OB, CO=OD, , так как вертикальные. Треугольник AOD =COB по двум сторонам и углу между ними. Из равенства треугольников -накрест лежащие углы. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. ADIICB.

Карточка №2

1. Прямая aIIb, c секущая 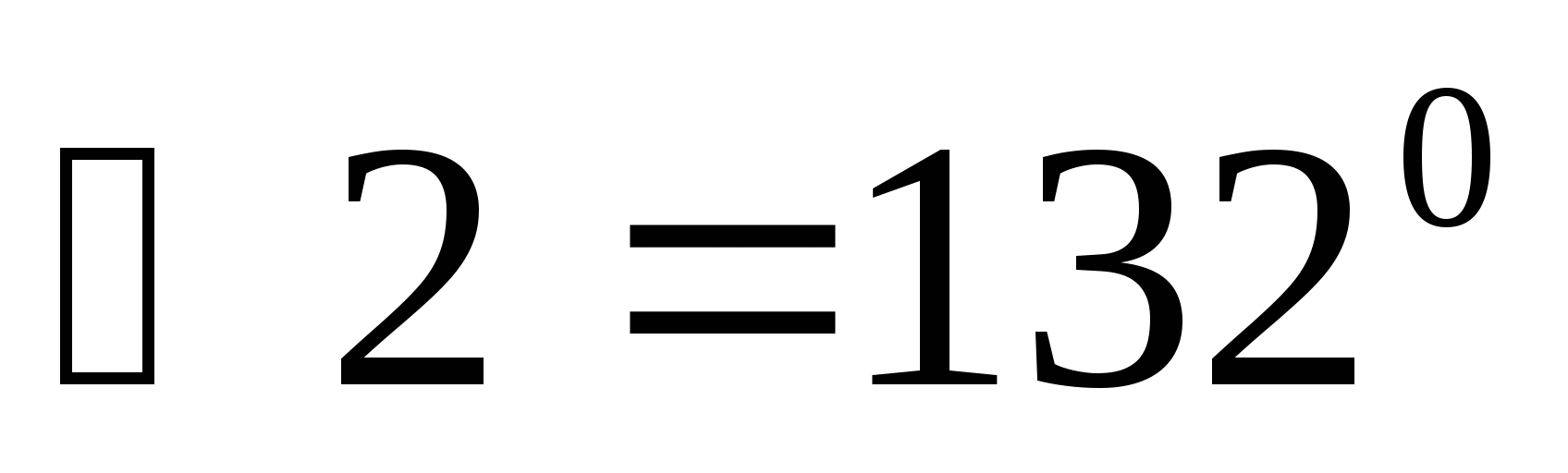. Найдите остальные углы.

1 2 5 6

4 3 8 7

2. ADIIBC, точка K середина отрезка AB

D

K B

A C

Докажите, что треугольник ADK равен треугольнику BCK.

Ответ

1. Дано: aIIb,

Найти: остальные углы

-односторонние углы

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰. , -накрест лежащие углы. -вертикальные углы, -вертикальные углы, -соответственные углы, -соответственные углы, -вертикальные углы, -вертикальные углы.

Ответ:

.

3. Дано : ADIIBC, AK=KB

Доказать

Доказательство:

AK=KB, -вертикальные углы , -накрест лежащие углы при пересечении ADIIBC секущей AB .

по стороне и двум прилежащим к ней углам.

Карточка №3.

1. B ABIICD , AB=CD, докажите , что треугольник ABO равен

треугольнику DCO.

A C

D

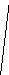
2.Доказать, что ABIICD A B

AO=OD

BO=OC O

C D

Ответ

1. Дано: ABIICD, AB=CD

Доказать:

Доказательство:

ABIICD, -накрест лежащие углы при пересечении ABIICD секущей АС. -накрест лежащие углы при пересечении ABIICD секущей AC

по стороне и двум прилежащим к ней углам.

2. Дано: AO=OB, CO=OD

Доказать: ABIICD

Доказательство:

Рассмотрим и , AO=OB,CO=OD , так как вертикальные.

=по двум сторонам и углу между ними. Из равенства и получаем, -накрест лежащие углы при пересечении прямых AB и СD секущей AD.Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны, следовательно, ABIICD.

Карточка №4 1.AB=BC AD=DE докажите, что DTIIAC.

B

D E

A C

2.Прямые AB, CD пересечены прямой BC , а . Могут ли прямые AB и CD быть параллельными?

Ответ

1. Дано: AB=BC, AD=DE, ,

Доказать: DEIIAC

Доказательство:

: AB=BC, -равнобедренный , -углы при основании равнобедренного треугольника .

AD=DE, -равнобедренный . -углы при основании равнобедренного треугольника. -накрест лежащие углы если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны, следовательно, DEIIAC.

2. Дано:

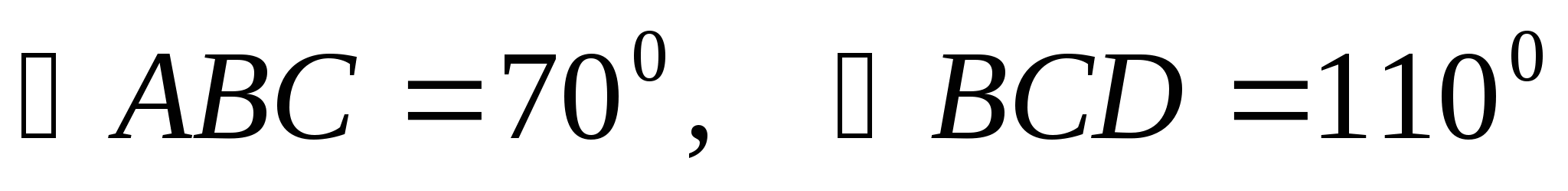
Могут ли прямые AB и СD быть параллельными?

Решение

Если и -односторонние

A

B

C

D

То,

Прямые AB и СD могут быть параллельны.

Карточка № 5

1. K B 2 , , .Найти .

11

3

4 D C

2. Параллельны ли прямые m и n.

m 128⁰

n

52⁰

Ответ:

1. Дано: .

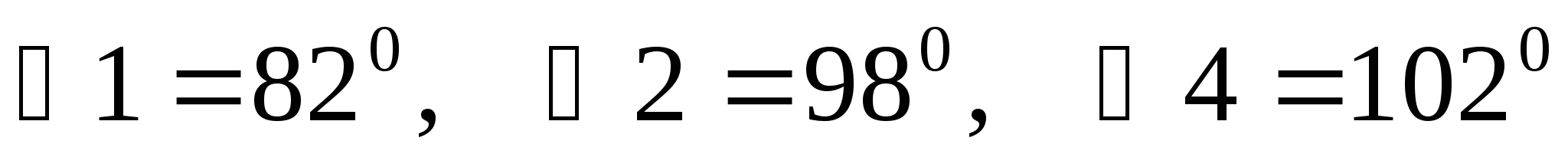Найти

Решение:

-вертикальные углы. -односторонние углы при переcечении прямых KD и BC cекущей KB. Если при пересечении двух пряых секущей сумма односторонних углов равно 180⁰, то прямые параллельны. KDIIBC.

- вертикальные углы -соответственные углы при пересечении KD и BC секущей DC.

Ответ:

2. Дано: m,n, 128⁰, 52⁰

Параллельны ли прямые m ,n ?

Решение:

-смежные углы. Угол 128⁰ и соответственные углы. Если две прямые пересечены секущей и соответственные углы равны, то прямые параллельны.

Следовательно, mIIn

Карточка № 6

1. На рисунке

P T PT=KM PK=TM , докажите ,что PTIIKM.

K M

2. На рисунке mIIn , , найти , .

m 3

2

n 1

Ответ

1.Дано:PT=KM, PK=TM

Доказать PTIIKM

Доказательство:

Рассмотрим и . PT=KM,PK=TM, KT-общая сторона. = по трем сторонам.из равенства треугольников следует -накрест лежащие углы при пересечении прямых PT и KM секущей KT. Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны. Следовательно, PTIIKM

2. Дано mIIn.

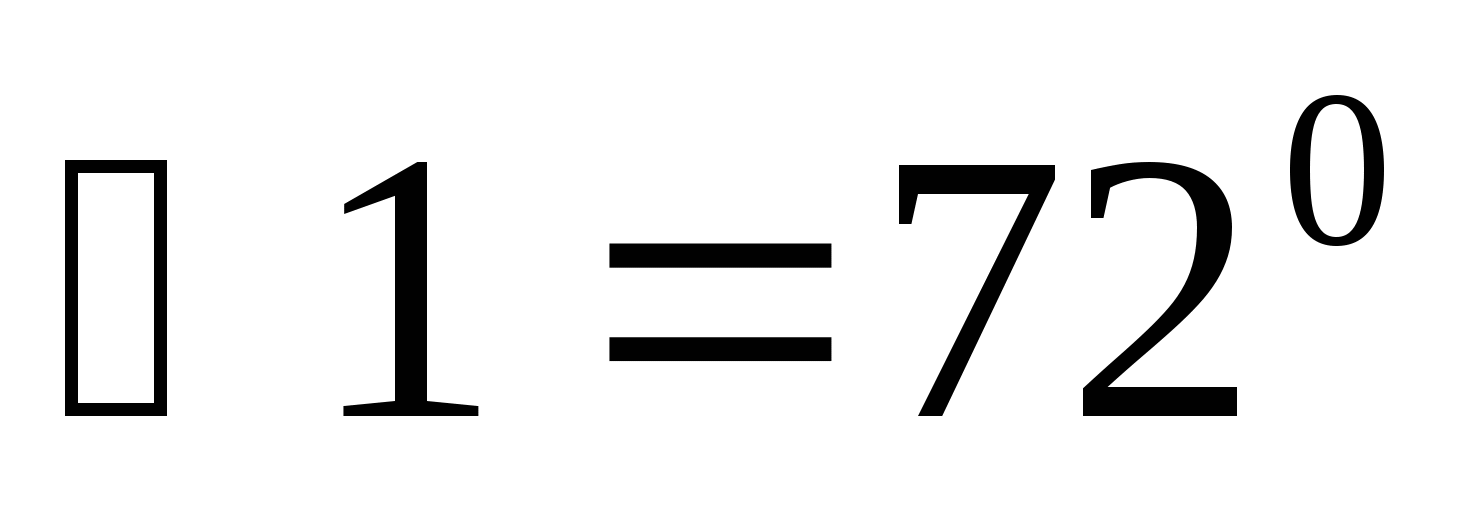
Найти:

Решение:

-соответственные углы при пересечении mIIn секущей С

-односторонние углы.

Ответ:и

4. Класс решает № 216. Один ученик у доски. В это время идет проверка индивидуальных заданий.

Дано: Решение.

D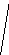E-биссектриса угла A E

1

Найти углы треугольника ADE 2 3 F

D

сумма односторонних углов равна 180 значит прямые АЕ и DF параллельны. и смежные. ( свойство смежных углов). =66⁰ так как DE-биссектриса угла .

=66⁰ накрест лежащие углы при пересечении AEIIDF секущей DE.

накрест лежащие углы при пересечении AEIIDF секущей AD.

Ответ: ,,.

Задача: на сколько частей разбивают плоскость:

1) одна прямая;

2) две параллельные прямые;

3) к параллельных прямых.

Решение.

1) Одна прямая разбивает плоскость на две части.

2) Две прямые разбивают плоскость на три части.

3) Пусть несколько прямых разбили плоскость на m частей. Проведем еще одну параллельную им прямую. Так как параллельные прямые не пересекаются, то новая прямая целиком лежит в одной из полученных ранее m частей и разбивает ее на две части. Это означает, что вместо одной прежней части стало две новых, то есть при проведении одной новой прямой прибавляется одна часть плоскости. k прямых разбивают плоскость на k+1 части.

5) Домашнее задание: № 214, 215

6) Проводится проверочная работа (12мин).

Вариант 1

1. На рисунке прямые m иn параллельны .

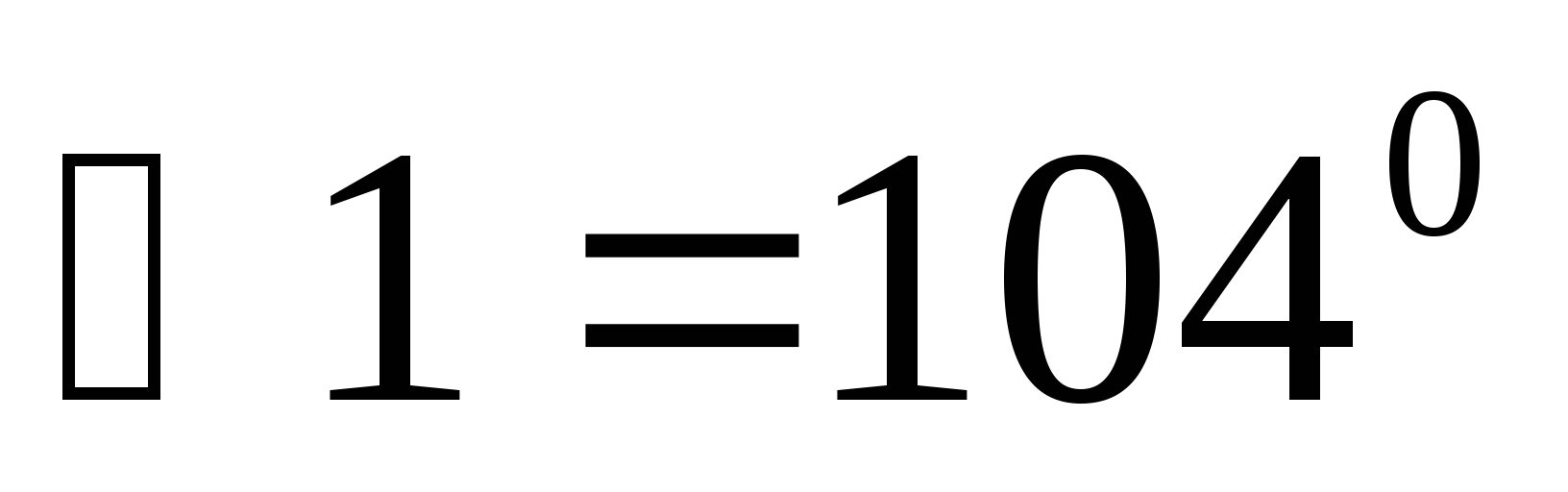m n

1 2 3

Найти: ,.

2. Через вершину прямого угла С треугольника ABC проведена прямая CD параллельная стороне AB найдите углы A и B треугольника, если.

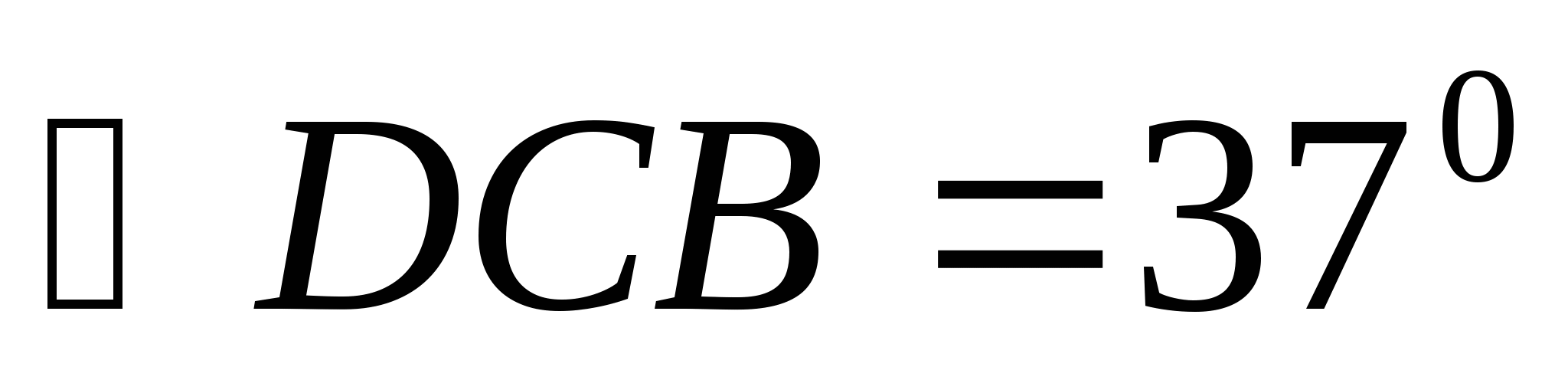Вариант 2

1.На рисунке прямые m иn параллельны .

a b

3 2 1

Найти : , .

2. Через вершину С треугольника CDE c прямым углом D проведена прямая CP параллельная прямой DE. Найдите углы C и E треугольника, если.

Проверочные работы собираются, затем проверяются учителем и оцениваются.

7)Подводится итог урока, выясняем, справились ли с поставленной целью, что понравилось, что еще хотелось бы повторить, что изменить в дальнейшей работе.

Сообщаются и комментируются оценки за ответы.

8) Резервные задания: № 218.