Прототипы для обучающихся 11 класса

1. Задание 1 № 24281. Налог на доходы составляет от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?

2. Задание 1 № 26629. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?

3. Задание 1 № 25101.

В летнем лагере 189 детей и 27 воспитателей. В автобус помещается не более 28 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?

4. Задание 1 № 77337. В школе есть трехместные туристические палатки. Какое наименьшее число палаток нужно взять в поход, в котором участвует 20 человек?

5. Задание 1 № 26620. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?

6. Задание 1 № 25379.

Таксист за месяц проехал 6000 км. Стоимость 1 литра бензина 21 рубль. Средний расход бензина на 100 км составляет 6 литров. Сколько рублей потратил таксист на бензин за этот месяц?

7. Задание 1 № 25255.

В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 300 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 6 недель?

8. Задание 1 № 77147. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 7900 рублей?

9. Задание 1 № 323511. В розницу один номер еженедельного журнала стоит 24 рубля, а полугодовая подписка на этот журнал стоит 460 рублей. За полгода выходит 25 номеров журнала. Сколько рублей можно сэкономить за полгода, если не покупать каждый номер журнала отдельно, а получать журнал по подписке?

10. Задание 1 № 77331. На счету Машиного мобильного телефона было 53 рубля, а после разговора с Леной осталось 8 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 2 рубля 50 копеек?

11. Задание 1 № 509077. Ананасы стоят 85 руб. за штуку. Какое максимальное число ананасов можно купить на 500 руб., если их цена снизится на 20%?

12. Задание 1 № 2497. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?

13. Задание 1 № 26635. В летнем лагере 218 детей и 26 воспитателей. В автобус помещается не более 45 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?

14. Задание 1 № 77355. Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов?

15. Задание 1 № 318581. Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

16. Задание 1 № 500947. В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт 3 пирога с черносливом. Для пирога на 10 человек следует взять фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 6 человек. Считайте, что 1 фунт равен 0,4 кг.

17. Задание 1 № 318949. Система навигации, встроенная в спинку самолетного кресла, информирует пассажира о том, что полет проходит на высоте 21 910 футов. Выразите высоту полета в метрах. Считайте, что 1 фут равен 30,5 см.

18. Задание 1 № 504421. По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 18 руб. Если на счету осталось меньше 18 руб., то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 800 руб. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?

19. Задание 1 № 25155.

Летом килограмм клубники стоит 60 рублей. Мама купила 2 кг 200 г клубники. Сколько рублей сдачи она должна получить с 200 рублей?

20. Задание 1 № 24429. В летнем лагере на каждого участника полагается 30 г сахара в день. В лагере 148 человек. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 5 дней?

21. Задание 2 № 512324. На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали - цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену никеля на момент закрытия торгов в указанный период. Ответ дайте в долларах США за тонну.

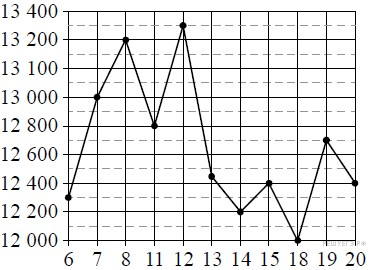
22. Задание 2 № 504551. На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали - средняя температура в градусах Цельсия. Определите по диаграмме наибольшую среднюю температуру в Минске в период с сентября по декабрь 2003 года. Ответ дайте в градусах Цельсия.

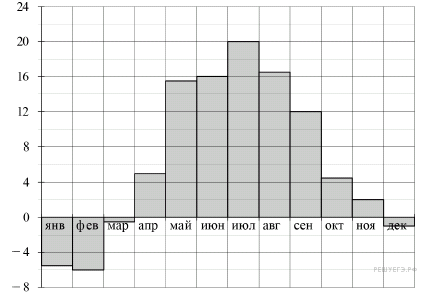
23. Задание 2 № 28759. На диаграмме показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря 2009 года. По горизонтали указывается номер часа, по вертикали - количество посетителей сайта за данный час. Определите по диаграмме разность наибольшего и наименьшего количества посетителей за час в данный день.

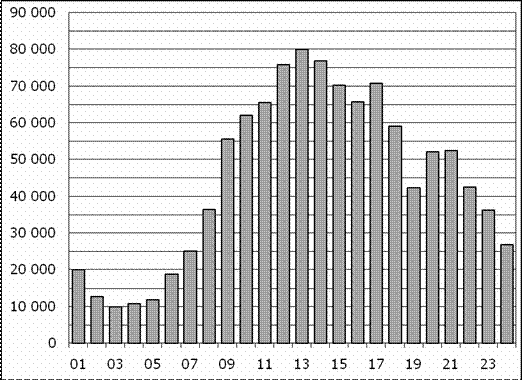
24. Задание 2 № 18889.

На рисунке жирными точками показано суточное количество осадков, выпадавших в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней за данный период не выпадало осадков.

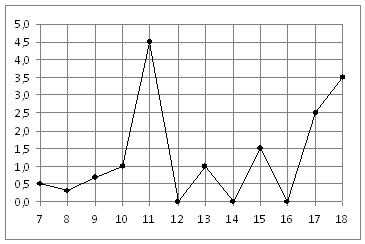
25. Задание 2 № 263801.

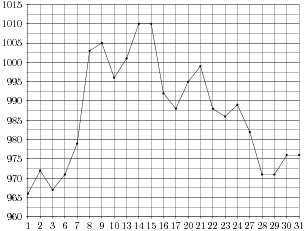
На рисунке жирными точками показана цена золота, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали - цена золота в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней за указанный период цена золота была ровно 1010 рублей за грамм.

26. Задание 2 № 263865. 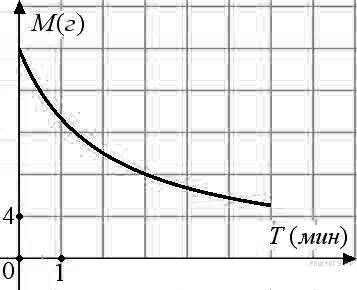В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. На оси абсцисс откладывается время в минутах, прошедшее с момента начала реакции, на оси ординат - масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?

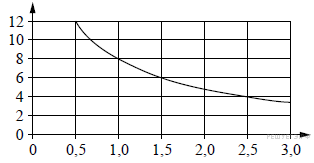
27. Задание 2 № 509566. Мощность отопителя в автомобиле регулируется дополнительным сопротивлением. При этом меняется сила тока в электрической цепи электродвигателя: чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На графике показана зависимость силы тока от величины сопротивления. На горизонтальной оси отмечено сопротивление в омах, на вертикальной оси - сила тока в амперах. Определите по графику, сколько ампер составляет сила тока в цепи при сопротивлении 1 Ом.

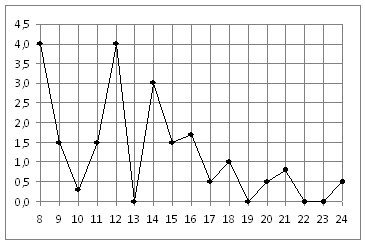
28. Задание 2 № 18893. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа за данный период впервые выпало ровно 1,5 миллиметра осадков.

29. Задание 2 № 263747.

На рисунке жирными точками показана цена палладия, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали - цена палладия в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену палладия в период с 15 по 27 октября. Ответ дайте в рублях за грамм.

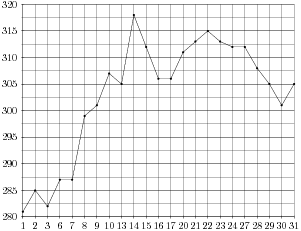
30. Задание 2 № 263977.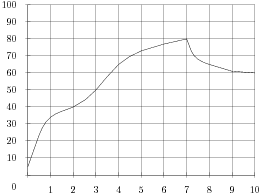

На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат - температура двигателя в градусах Цельсия. Определите по графику, до скольки градусов Цельсия двигатель нагрелся за первые 7 минут.

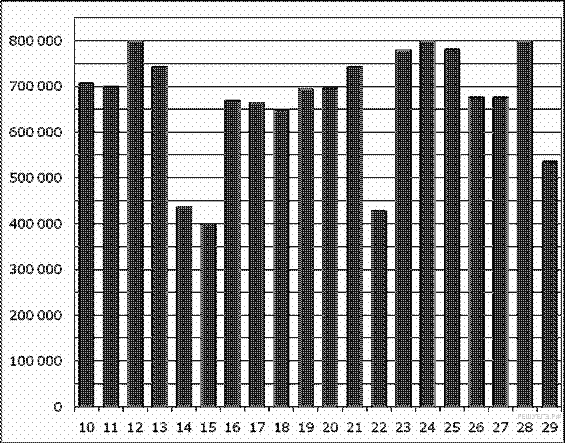
31. Задание 2 № 28762. На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали - количество посетителей сайта за данный день. Определите по диаграмме, какого числа количество посетителей сайта РИА Новости было наименьшим за указанный период.

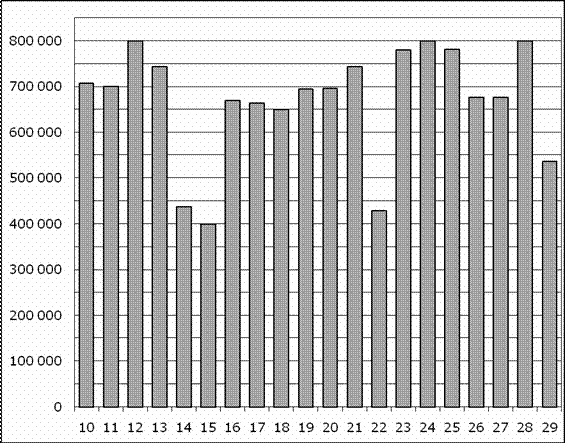
32. Задание 2 № 28743.

На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали - количество посетителей сайта за данный день. Определите по диаграмме, сколько было дней за данный период, когда на сайте РИА Новости было менее полумиллиона посетителей.

33. Задание 2 № 263983.

На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат - температура двигателя в градусах Цельсия.

Определите по графику, сколько минут двигатель нагревался до температуры .

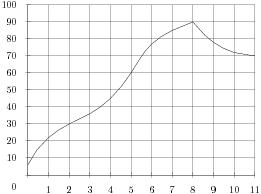
34. Задание 2 № 263609. На рисунке жирными точками показан курс австралийского доллара, установленный Центробанком РФ, во все рабочие дни с 1 по 27 октября 2010 года. По горизонтали указываются числа месяца, по вертикали - цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какой был курс доллара 12 октября. Ответ дайте в рублях.

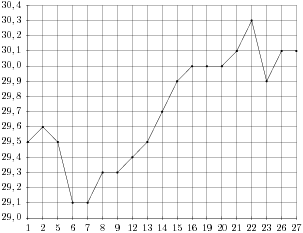
35. Задание 2 № 27516. На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.

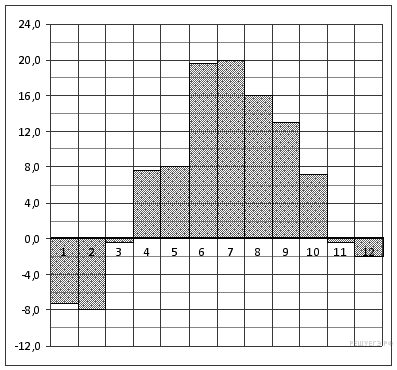
36. Задание 2 № 5377.

На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 19 февраля. Ответ дайте в градусах Цельсия.

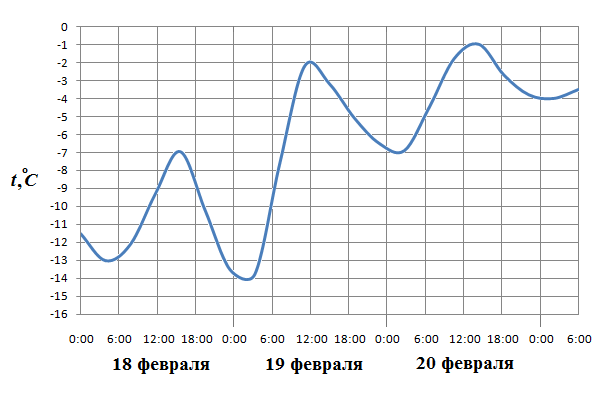
37. Задание 2 № 507896. На графике показано изменение температуры двигателя в процессе разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат - температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель со второй по пятую минуту разогрева.

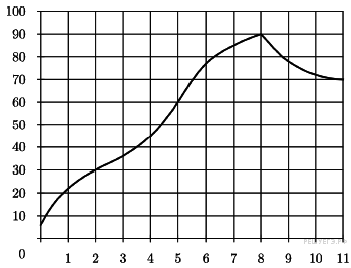
38. Задание 2 № 27528. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали - количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

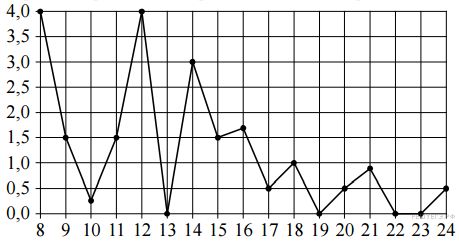
39. Задание 2 № 5369.

На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 9 августа. Ответ дайте в градусах Цельсия.

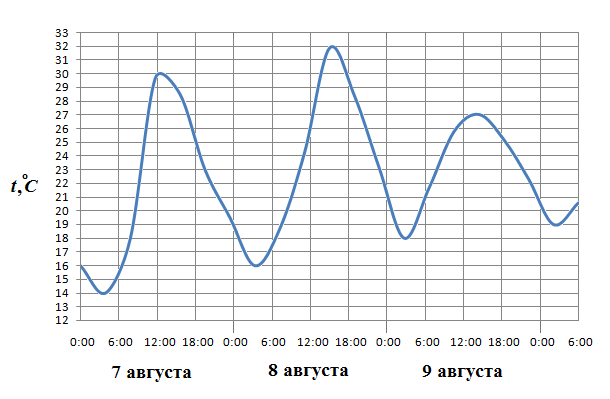
40. Задание 2 № 26875. На рисунке жирными точками показана цена олова на момент закрытия биржевых торгов во все рабочие дни с 3 по 18 сентября 2007 года. По горизонтали указываются числа месяца, по вертикали - цена тонны олова в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена олова на момент закрытия торгов была наибольшей за данный период.

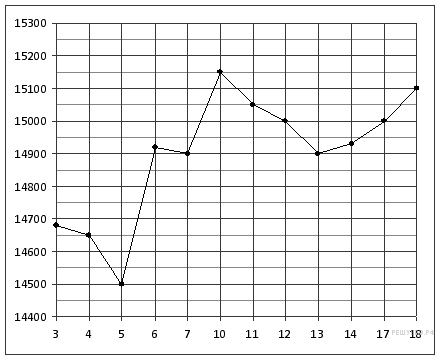
41. Задание 3 № 27720. 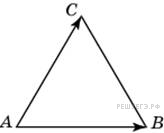Стороны правильного треугольника равны . Найдите длину вектора .

42. Задание 3 № 60055. Найдите площадь трапеции, вершины которой имеют координаты (1; 13), (6; 15), (6; 21), (1; 17).

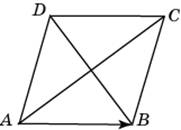
43. Задание 3 № 60455. Диагонали ромба ABCD равны 40 и 42. Найдите длину вектора .

44. Задание 3 № 26074.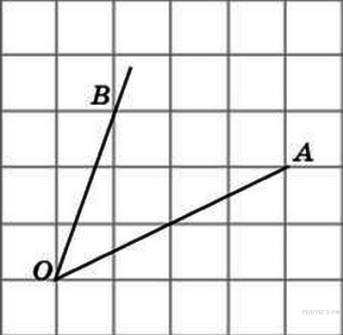

Найдите тангенс угла AOB.

45. Задание 3 № 508989. 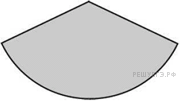Из круга с радиусом 9 вырезан сектор, площадь которого равна 27. Найдите длину дуги сектора.

46. Задание 3 № 61005. Вектор с началом в точке имеет координаты . Найдите ординату точки

47. Задание 3 № 27831. 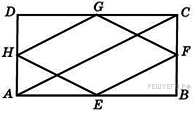Середины сторон прямоугольника, диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.

48. Задание 3 № 27709. Две стороны прямоугольника равны 6 и 8. Найдите длину разности векторов и .

49. Задание 3 № 27728. 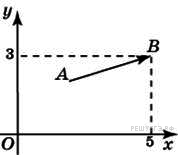Вектор с концом в точке (5; 3) имеет координаты (3; 1). Найдите ординату точки .

50. Задание 3 № 55905. Периметр прямоугольника равен 42, а площадь 108. Найдите большую сторону прямоугольника.

51. Задание 3 № 27726.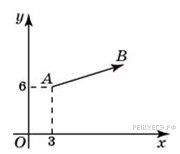

Вектор с началом в точке A(3; 6) имеет координаты (9; 3). Найдите сумму координат точки B.

52. Задание 3 № 246701.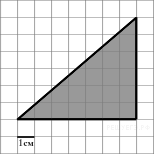

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

53. Задание 3 № 55049. 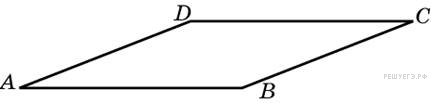Найдите площадь ромба, если его стороны равны 23, а один из углов равен 150°.

54. Задание 3 № 60855. Стороны правильного треугольника ABCравны 38. Найдите длину вектора

55. Задание 3 № 27587. 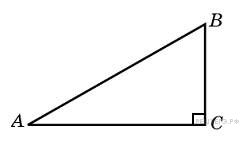Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.

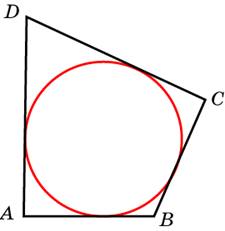
56. Задание 3 № 54551.

В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.

57. Задание 3 № 27794. 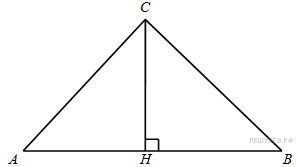В треугольнике ABCAC = BC, AB = 4, высота CH равна . Найдите угол . Ответ дайте в градусах.

58. Задание 3 № 27767. 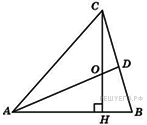В треугольнике ABC CH - высота, AD - биссектриса, O - точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах.

59. Задание 3 № 322727. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры.

60. Задание 3 № 24279.

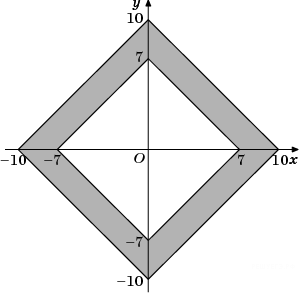Найдите площадь закрашенной фигуры на координатной плоскости.

61. Задание 4 № 500997. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.

62. Задание 4 № 320641. Вероятность того, что новый тостер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,8. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

63. Задание 4 № 282857. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

64. Задание 4 № 286383. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 6 прыгунов из Голландии и 2 прыгуна из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четырнадцатым будет выступать прыгун из Аргентины.

65. Задание 4 № 325913. За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки не будут сидеть рядом.

66. Задание 4 № 1003. На экзамене 45 билетов, Федя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.

67. Задание 4 № 320170. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?

68. Задание 4 № 324629.

Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8С, равна 0,92. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8С или выше.

69. Задание 4 № 1009. Люба включает телевизор. Телевизор включается на случайном канале. В это время по шести каналам из сорока восьми показывают документальные фильмы. Найдите вероятность того, что Люба попадет на канал, где документальные фильмы не идут.

70. Задание 4 № 320197. Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.

71. Задание 4 № 320178. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?

72. Задание 4 № 320208. В кармане у Миши было четыре конфеты - «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».

73. Задание 4 № 285926. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.

74. Задание 4 № 320180. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

75. Задание 4 № 319553. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,56. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

76. Задание 4 № 320211. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

77. Задание 4 № 286115. Конкурс исполнителей проводится в 5 дней. Всего заявлено 65 выступлений - по одному от каждой страны. В первый день 13 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

78. Задание 4 № 512389. В классе 21 учащийся, среди них два друга - Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе.

79. Задание 4 № 1006. Маша включает телевизор. Телевизор включается на случайном канале. В это время по девяти каналам из сорока пяти показывают новости. Найдите вероятность того, что Маша попадет на канал, где новости не идут.

80. Задание 4 № 283477. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет все три раза.

81. Задание 5 № 14669.

Найдите корень уравнения:

82. Задание 5 № 26662. Найдите корень уравнения: .

83. Задание 5 № 26654. Найдите корень уравнения .

84. Задание 5 № 105697. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них.

85. Задание 5 № 101881. Решите уравнение .

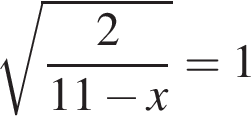86. Задание 5 № 500951. Решите уравнение

87. Задание 5 № 510483. Найдите корень уравнения

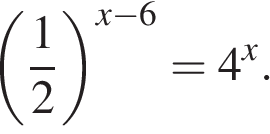
88. Задание 5 № 509012. Найдите корень уравнения

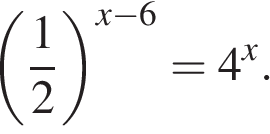
89. Задание 5 № 77376. Решите уравнение . В ответе напишите наибольший отрицательный корень.

90. Задание 5 № 101379.

Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

91. Задание 5 № 3227.

Найдите корень уравнения .

92. Задание 5 № 13375. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

93. Задание 5 № 11649. Найдите корень уравнения:

94. Задание 5 № 26650. Найдите корень уравнения .

95. Задание 5 № 12891. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

96. Задание 5 № 508129. Найдите корень уравнения

Выберите одно из предложенных заданий и решите его.

97. Задание 5 № 26665. Найдите корень уравнения: . Если уравнение имеет более одного корня, в ответе укажите больший из них.

98. Задание 5 № 26658. Найдите корень уравнения .

99. Задание 5 № 2997.

Найдите корень уравнения .

100. Задание 5 № 77373. Решите уравнение .

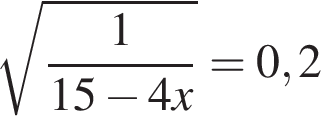101. Задание 6 № 56807. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.

102. Задание 6 № 27837. 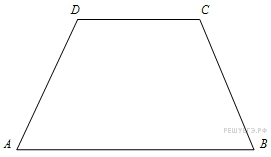Основания равнобедренной трапеции равны 15 и 9, один из углов равен . Найдите высоту трапеции.

103. Задание 6 № 27451. 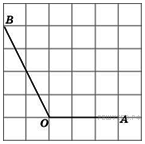Найдите синус угла . В ответе укажите значение синуса, умноженное на .

104. Задание 6 № 27621. 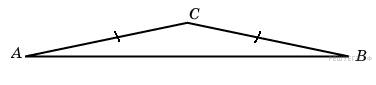Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100.

105. Задание 6 № 53365. Найдите радиус окружности, вписанной в квадрат со стороной 20.

106. Задание 6 № 27799. 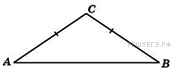В треугольнике , угол равен , . Найдите .

107. Задание 6 № 27387. 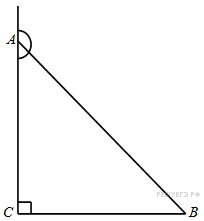В треугольнике угол равен 90°, синус внешнего угла при вершине равен . Найдите .

108. Задание 6 № 27952. Найдите радиус окружности, вписанной в четырехугольник . Считайте, что стороны квадратных клеток равны 1. В ответе укажите .

109. Задание 6 № 34829. В треугольнике ABC угол C равен 90°, . Найдите косинус внешнего угла при вершине A.

110. Задание 6 № 27352. 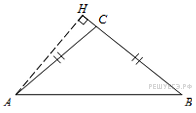В тупоугольном треугольнике , высота равна 24, . Найдите .

111. Задание 6 № 27259. В треугольнике АВС угол С равен 90°, СН - высота, , . Найдите АН.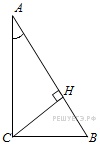

112. Задание 6 № 27225. 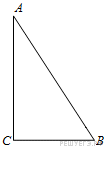В треугольнике угол равен 90°, . Найдите .

113. Задание 6 № 31793. 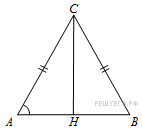В треугольнике ABC AC = BC = 20,5, Найдите AB.

114. Задание 6 № 53013. 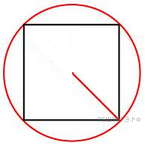Найдите сторону квадрата, вписанного в окружность радиуса

115. Задание 6 № 27409.

В треугольнике угол равен 90°, тангенс внешнего угла при вершине равен , . Найдите .

116. Задание 6 № 27305. В треугольнике АВС АС = ВС, высота СН равна 7, АВ = 48. Найдите .

117. Задание 6 № 4819. 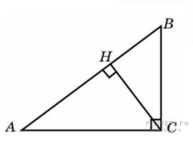В треугольнике ABC угол C равен ,CH - высота, AB = 5, Найдите BH.

118. Задание 6 № 29109. 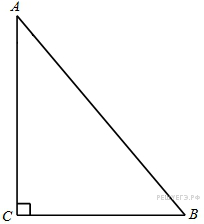В треугольнике ABC угол C равен 90°,. Найдите .

119. Задание 6 № 35109. 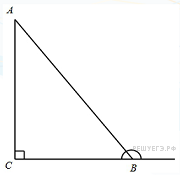В треугольнике ABC угол C равен 90°, . Найдите синус внешнего угла при вершине B.

120. Задание 6 № 27341. 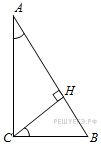В треугольнике ABC угол C равен 90°, высота CHравна 4, . Найдите .

121. Задание 7 № 40130. 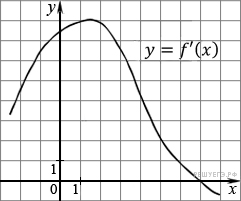На рисунке изображен график производной функции . Найдите абсциссу точки, в которой касательная к графику параллельна прямой или совпадает с ней.

122. Задание 7 № 9627. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .

123. Задание 7 № 323175. На рисунке изображён график функции и одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

124. Задание 7 № 9641.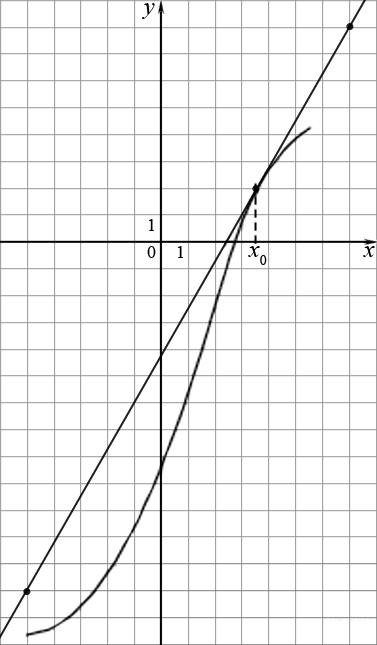

На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

125. Задание 7 № 8545.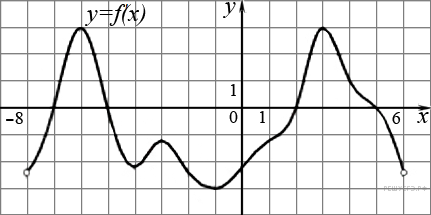

На рисунке изображен график производной функции f(x), определенной на интервале (−8; 6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

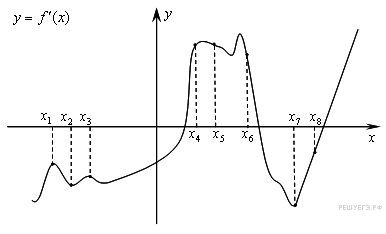
126. Задание 7 № 317541. На рисунке изображён график (x) производной функции f(x) и восемь точек на оси абсцисс: x₁, x₂, x₃, ..., x₈. В скольких из этих точек функция f(x) возрастает?

127. Задание 7 № 505166. 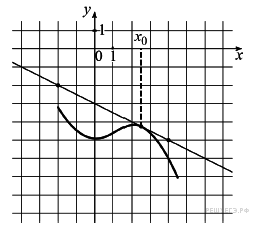На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

128. Задание 7 № 7549. На рисунке изображен график функции y = f(x), определенной на интервале (−5; 7). Найдите сумму точек экстремума функции y = f(x).

129. Задание 7 № 27488. 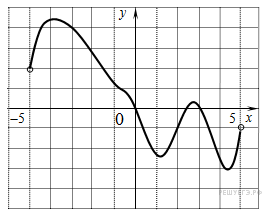На рисунке изображен график функции , определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции отрицательна.

130. Задание 7 № 8299. 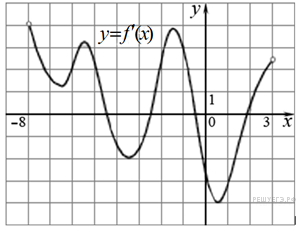На рисунке изображен график y=f'(x) - производной функции f(x), определенной на интервале (−8; 3). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

131. Задание 7 № 323477. На рисунке изображён график некоторой функции . Функция - одна из первообразных функции . Найдите площадь закрашенной фигуры.

132. Задание 7 № 121211. Прямая является касательной к графику функции . Найдите b, учитывая, что абсцисса точки касания больше 0.

133. Задание 7 № 323373. 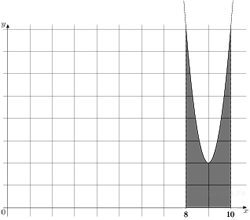На рисунке изображён график некоторой функции . Функция - одна из первообразных функции . Найдите площадь закрашенной фигуры.

134. Задание 7 № 9561. 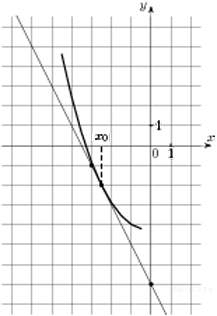На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .

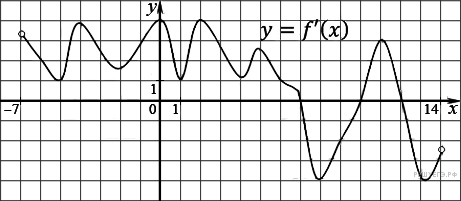
135. Задание 7 № 27494. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

136. Задание 7 № 6871. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.

137. Задание 7 № 9635. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

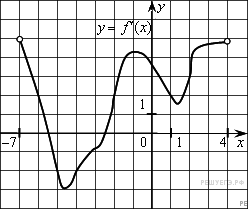
138. Задание 7 № 27497. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

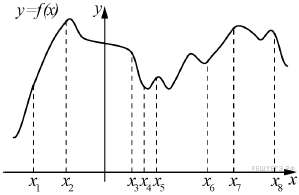
139. Задание 7 № 510485. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x₁, x₂, x₃, …, x₈. В скольких из этих точек производная функции f(x) положительна?

140. Задание 7 № 123215.

Материальная точка движется прямолинейно по закону (гдеx - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 4 с.

141. Задание 8 № 245377. 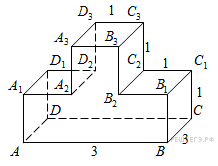Найдите квадрат расстояния между вершинами B и D₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

142. Задание 8 № 75225. 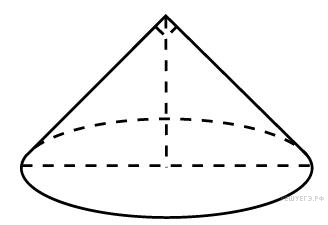Диаметр основания конуса равен 66, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на .

143. Задание 8 № 27091.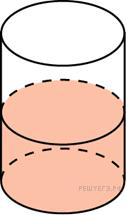

В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.

144. Задание 8 № 245366. 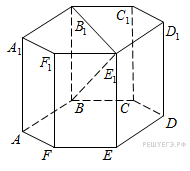В правильной шестиугольной призме все ребра равны Найдите расстояние между точками и

145. Задание 8 № 27063. 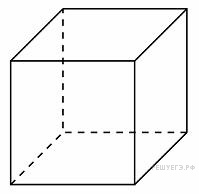Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

146. Задание 8 № 74695.

Через среднюю линию основания треугольной призмы, объем которой равен 18, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

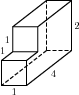
147. Задание 8 № 25551.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

148. Задание 8 № 509015. 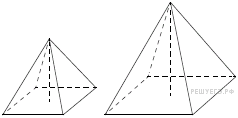Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 16. У второй пирамиды высота в 2 раза больше, а сторона основания в 1,5 раза больше, чем у первой. Найдите объём второй пирамиды.

149. Задание 8 № 75465.

Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 36 раз?

150. Задание 8 № 27181. 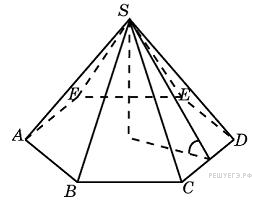Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45. Найдите объем пирамиды.

151. Задание 8 № 76781. 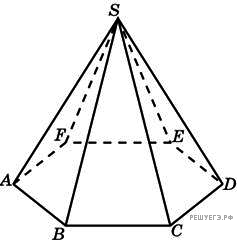Сторона основания правильной шестиугольной пирамиды равна 10, боковое ребро равно 20. Найдите объем пирамиды.

152. Задание 8 № 245367. 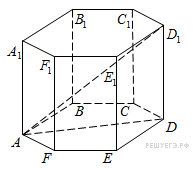В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла

153. Задание 8 № 76487. 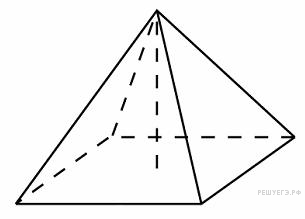Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 24 и высота равна 16.

154. Задание 8 № 76299. Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

155. Задание 8 № 501747.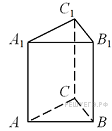

Найдите объём многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 3, а боковое ребро равно 2.

156. Задание 8 № 74895. 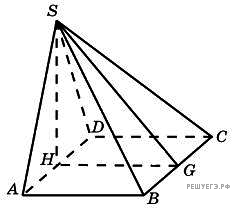Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 12. Найдите объем пирамиды.

157. Задание 8 № 75963.

В основании прямой призмы лежит ромб с диагоналями, равными 16 и 30. Площадь ее поверхности равна 2588. Найдите боковое ребро этой призмы.

158. Задание 8 № 281867. 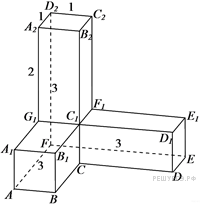Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

159. Задание 8 № 505464. 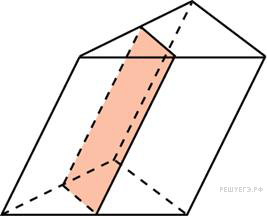Через среднюю линию основания треугольной призмы, объем которой равен 52, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

160. Задание 8 № 27206. Вершина куба со стороной 1,6 является центром сферы, проходящей через точку . Найдите площадь части сферы, содержащейся внутри куба. В ответе запишите величину .

161. Задание 9 № 26891.

Найдите значение выражения .

162. Задание 9 № 509992. Найдите значение выражения

163. Задание 9 № 26977. Найдите значение выражения .

164. Задание 9 № 77408. Найдите значение выражения .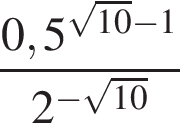

165. Задание 9 № 65551.

Найдите значение выражения , если .

166. Задание 9 № 26852. Найдите значение выражения .

167. Задание 9 № 26844. Найдите значение выражения .

168. Задание 9 № 505168. Найдите значение выражения

169. Задание 9 № 26898. Найдите значение выражения при .

170. Задание 9 № 69767.

Найдите значение выражения .

171. Задание 9 № 89483.

Найдите значение выражения при .

172. Задание 9 № 26808. Найдите значение выражения .

173. Задание 9 № 26782. Найдите значение выражения .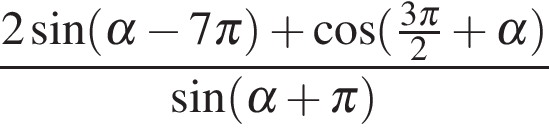

174. Задание 9 № 85485. Найдите значение выражения при .

175. Задание 9 № 77405. Найдите значение выражения .

176. Задание 9 № 26925. Найдите значение выражения .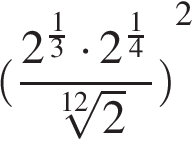

177. Задание 9 № 26947. Найдите значение выражения .

178. Задание 9 № 27003. Найдите значение выражения при .

179. Задание 9 № 26818. Найдите значение выражения , если .

180. Задание 9 № 77392. Найдите значение выражения .

181. Задание 10 № 41341.

Высота над землeй подброшенного вверх мяча меняется по закону , где - высота в метрах, - время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?

182. Задание 10 № 28081. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , где t - время в секундах, прошедшее с момента открытия крана, м - начальная высота столба воды, - отношение площадей поперечных сечений крана и бака, а g - ускорение свободного падения (считайте м/с). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

183. Задание 10 № 27964. Мотоциклист, движущийся по городу со скоростью км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением км/ч. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.

184. Задание 10 № 28015. При температуре рельс имеет длину м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону , где - коэффициент теплового расширения, - температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ выразите в градусах Цельсия.

185. Задание 10 № 28205. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием см. Расстояние от линзы до лампочки может изменяться в пределах от 55 до 70 см, а расстояние от линзы до экрана - в пределах от 260 до 300 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.

186. Задание 10 № 27956. Зависимость объeма спроса (единиц в месяц) на продукцию предприятия - монополиста от цены (тыс. руб.) задаeтся формулой . Выручка предприятия за месяц (в тыс. руб.) вычисляется по формуле . Определите наибольшую цену , при которой месячная выручка составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.

187. Задание 10 № 28519. Мяч бросили под углом к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле . При каком наименьшем значении угла (в градусах) время полeта будет не меньше 1,9 секунды, если мяч бросают с начальной скоростью м/с? Считайте, что ускорение свободного падения м/с.

188. Задание 10 № 41421.

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , где м - начальный уровень воды, м/мин², и м/мин - постоянные, - время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

189. Задание 10 № 42997. Eмкость высоковольтного конденсатора в телевизоре Ф. Параллельно с конденсатором подключeн резистор с сопротивлением Ом. Во время работы телевизора напряжение на конденсаторе кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением (с), где - постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 25,2 с?

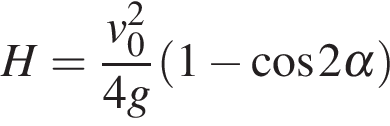190. Задание 10 № 28577. Небольшой мячик бросают под острым углом к плоской горизонтальной поверхности земли. Максимальная высота полeта мячика, выраженная в метрах, определяется формулой , где м/с - начальная скорость мячика, а g - ускорение свободного падения (считайте м/с). При каком наименьшем значении угла (в градусах) мячик пролетит над стеной высотой 2,2 м на расстоянии 1 м?

191. Задание 10 № 27959. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону где - время в секундах, прошедшее с момента открытия крана, - начальная высота столба воды, - отношение площадей поперечных сечений крана и бака, а - ускорение свободного падения (считайте м/с). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

192. Задание 10 № 42787. При адиабатическом процессе для идеального газа выполняется закон где - давление в газе в паскалях, - объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него ) из начального состояния, в котором Па , газ начинают сжимать. Какой наибольший объeм может занимать газ при давлениях не ниже Па? Ответ выразите в кубических метрах.

193. Задание 10 № 27979. К источнику с ЭДС В и внутренним сопротивлением Ом, хотят подключить нагрузку с сопротивлением Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даeтся формулой . При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 50 В? Ответ выразите в Омах.

194. Задание 10 № 28289. Опорные башмаки шагающего экскаватора, имеющего массу тонн представляют собой две пустотелые балки длиной метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой, где m - масса экскаватора (в тоннах), l - длина балок в метрах, s - ширина балок в метрах, g - ускорение свободного падения (считайте м/с). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 200 кПа. Ответ выразите в метрах.

195. Задание 10 № 27990. При адиабатическом процессе для идеального газа выполняется закон, где - давление в газе в паскалях, - объeм газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него ) из начального состояния, в котором Пам⁵, газ начинают сжимать. Какой наибольший объeм может занимать газ при давлениях не ниже Па? Ответ выразите в кубических метрах.

196. Задание 10 № 27968. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: , где - постоянная, - радиус аппарата в метрах, кг/м³ - плотность воды, а - ускорение свободного падения (считайте Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах.

197. Задание 10 № 41999.

Сила тока в цепи (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: , где - напряжение в вольтах, - сопротивление электроприбора в омах. В электросеть включeн предохранитель, который плавится, если сила тока превышает 2,5 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в омах.

198. Задание 10 № 43333.

Небольшой мячик бросают под острым углом к плоской горизонтальной поверхности земли. Расстояние, которое пролетает мячик, вычисляется по формуле 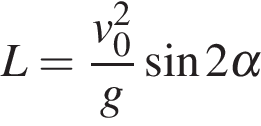(м), где м/с - начальная скорость мячика, а - ускорение свободного падения (считайте м/с). При каком наименьшем значении угла (в градусах) мячик перелетит реку шириной 14,4 м?

199. Задание 10 № 505403. Расстояние от наблюдателя, находящегося на небольшой высоте километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле где - радиус Земли. С какой высоты горизонт виден на расстоянии 144 километров? Ответ выразите в километрах.

200. Задание 10 № 41371.

В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону , где - время в секундах, прошедшее с момента открытия крана, м - начальная высота столба воды, - отношение площадей поперечных сечений крана и бака, а - ускорение свободного падения (считайте м/с). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

201. Задание 11 № 113441.

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 25 метрам?

202. Задание 11 № 107401.

Семь рубашек дешевле куртки на 2%. На сколько процентов десять рубашек дороже куртки?

203. Задание 11 № 27482. Пристани и расположены на озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью из в . На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из в . Найдите скорость баржи на пути из в . Ответ дайте в км/ч.

204. Задание 11 № 500959. Смешав 41-процентный и 63-процентный растворы кислоты и добавив 10 кг чистой воды, получили 49-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 54-процентный раствор кислоты. Сколько килограммов 41-процентного раствора использовали для получения смеси?

205. Задание 11 № 99609. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.

206. Задание 11 № 108655. В сосуд, содержащий 8 литров 24-процентного водного раствора некоторого вещества, добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора?

207. Задание 11 № 39999.

Первая труба пропускает на 8 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 660 литров она заполняет на 11 минут дольше, чем вторая труба заполняет резервуар объемом 570 литров?

208. Задание 11 № 40053.

Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 638 литров она заполняет на 7 минут быстрее, чем первая труба заполняет резервуар объемом 812 литров?

209. Задание 11 № 112207. Бизнесмен Печенов получил в 2000 году прибыль в размере 1 000 000 рублей. Каждый следующий год его прибыль увеличивалась на 16% по сравнению с предыдущим годом. Сколько рублей заработал Печенов за 2002 год?

210. Задание 11 № 108485. Дима, Антон, Паша и Коля учредили компанию с уставным капиталом 100 000 рублей. Дима внес 22% уставного капитала, Антон - 50 000 рублей, Паша - 0,26 уставного капитала, а оставшуюся часть капитала внес Коля. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 700 000 рублей причитается Коле? Ответ дайте в рублях.

211. Задание 11 № 109111.

Имеется два сплава. Первый сплав содержит 10% никеля, второй - 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

212. Задание 11 № 5733. Теплоход проходит по течению реки до пункта назначения 391 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 3 км/ч, стоянка длится 6 часов, а в пункт отправления теплоход возвращается через 46 часов после отплытия из него. Ответ дайте в км/ч.

213. Задание 11 № 26584. Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

214. Задание 11 № 40121. Пристани A и B расположены на озере, расстояние между ними 270 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 1 км/ч больше прежней, сделав по пути остановку на 3 часа. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.

215. Задание 11 № 115257. Путешественник переплыл море на яхте со средней скоростью 21 км/ч. Обратно он летел на спортивном самолете со скоростью 567 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ ч.

216. Задание 11 № 99568. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?

217. Задание 11 № 5881. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?

218. Задание 11 № 107387. В 2008 году в городском квартале проживало 40 000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 3%, а в 2010 году - на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?

219. Задание 11 № 505468. Имеется два сплава. Первый сплав содержит 10% никеля, второй - 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?

220. Задание 11 № 111911. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 9 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 18 метрам.

221. Задание 12 № 130561. Найдите наименьшее значение функции на отрезке .

222. Задание 12 № 129873. Найдите точку минимума функции .

223. Задание 12 № 70437.

Найдите наибольшее значение функции на отрезке .

224. Задание 12 № 77461. Найдите точку минимума функции

225. Задание 12 № 245175. Найдите наименьшее значение функции .

226. Задание 12 № 282860. Найдите точку минимума функции .

227. Задание 12 № 129903. Найдите наименьшее значение функции на отрезке .

228. Задание 12 № 26691. Найдите наименьшее значение функции на отрезке .

229. Задание 12 № 124975. Найдите точку минимума функции .

230. Задание 12 № 77487. Найдите точку максимума функции .

231. Задание 12 № 127185. Найдите точку максимума функции .

232. Задание 12 № 508970. Найдите точку минимума функции

233. Задание 12 № 77481. Найдите наибольшее значение функции на отрезке .

234. Задание 12 № 127533. Найдите точку минимума функции .

235. Задание 12 № 3781. Найдите точку минимума функции .

236. Задание 12 № 510511. Найдите наименьшее значение функции на отрезке

237. Задание 12 № 3865. Найдите наибольшее значение функции на отрезке [−4,5; 0].

238. Задание 12 № 284125.

Найдите наименьшее значение функции на отрезке .

239. Задание 12 № 77498. Найдите наибольшее значение функции на отрезке .

240. Задание 12 № 287403.

Найдите точку максимума функции .