- Учителю
- Конспект урока по теме Решение тригонометрических уравнений. Отбор корней
Конспект урока по теме Решение тригонометрических уравнений. Отбор корней
Тема: Решение тригонометрических уравнений.
Отбор корней.
Цели урока:
-
Образовательные - обеспечить повторение, обобщение и систематизацию материала темы.
-
Развивающие - способствовать формированию умений применять приемы отбора корней при решении тригонометрических уравнений.
-
Воспитательные - содействовать воспитанию интереса к математике и ее приложениям, активности, общей культуры.
Тип урока: урок обобщения и систематизации знаний.
План урока.
-
Оргмомент.
-
Устный счет.
-
Решение тригонометрических уравнений. Отбор корней по заданным
условиям.
-
Выполнение упражнений.
-
Итоги урока.
-
Домашнее задание.
-
Организационный момент
На предыдущем уроке мы повторили решение тригонометрических уравнений. Мы знаем, что распространены задачи в которых требуется провести некоторое исследование корней тригонометрического уравнения. В результате такого исследования, как правило, какая-то часть полученных корней выбирается или, наоборот, отбрасывается на основании явно или неявно указанного в задаче признака. На сегодняшнем уроке будем учиться проводить отбор корней при решении тригонометрического уравнения.
-
Устный счет
а) Выясните, что больше: sin ![]() или cos
или cos ![]() ; sin
; sin ![]() или cos
или cos ![]() .
.
б) Упростите выражение: sin4 + cos2 cos4; cos4 + sin2 sin4.
в) Решите уравнение : sin x = ![]() , x
, x![]() ;
cos x =
;
cos x = ![]() ,
x
,
x![]() .
.
-
Решение тригонометрических уравнений. Отбор корней по заданным
условиям.
Решение некоторых тригонометрических уравнений предполагает последующую проверку условий, которым должны удовлетворять найденные корни. Наименее хлопотная ситуация возникает тогда, когда отбор корней удается провести без непосредственного их выписывания. При этом требуется лишь минимальные затраты усилий, связанные с выводом определенных следствий из уравнений с помощью формул тригонометрии.
Пример1. Найти все корни уравнения sin x cos ![]() + cos x sin
+ cos x sin ![]() =
= ![]()
расположенные в промежутке 3/2; .
Решение: sin x cos ![]() + cos x sin
+ cos x sin ![]() =
= ![]()
sin ![]() =
= ![]() ,
,
x = ![]() + (1)n
+ (1)n![]() ,
nZ,
,
nZ,
Ответ: ![]() .
.
Пример2. Решить уравнение: ![]() (sin 2x 3cos x) = 0.
(sin 2x 3cos x) = 0.
Решение: ![]() (sin 2x 3cos x) = 0
(sin 2x 3cos x) = 0
![]() cosx
(sin x
cosx
(sin x ![]() ) = 0,
) = 0,
уравнение равносильно совокупности уравнений и систем:
1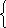 )
(2 - х)(2 +х) =0 2) cos x = 0
)
(2 - х)(2 +х) =0 2) cos x = 0
x = 2, x = 2; 2 x 2
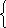 x
=
x
= ![]() + n, nZ;
+ n, nZ;
2 ![]() + n 2
+ n 2
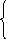 x
=
x
= ![]() + n, nZ;
+ n, nZ;
2![]() n 1
n 1![]() .
x =
.
x = ![]() + n, n = 2, 1, 0, 1.
+ n, n = 2, 1, 0, 1.
Ответ: 2, 1![]() ,
,
![]() ,
,
![]() , 1
, 1![]() ,
2.
,
2.
Пример 3. Найти наименьший положительный корень уравнения.
cos x2 = cos (x2 + 2x + 1).
Р
 ешение:
cos (x)2 cos ((x2 + 2x + 1)) = 0; sin
ешение:
cos (x)2 cos ((x2 + 2x + 1)) = 0; sin
![]() sin
sin ![]() =0;
=0;
2x + 1 = 2n, nZ;
2 x2
+ 2x 1 =2m, mZ
x2
+ 2x 1 =2m, mZ![]()
x
 = n
= n ![]() , nZ;
, nZ;
x = ![]() , mN;
, mN;
x =
= ![]() , mN.
, mN.
Наименьший положительный корень равен ![]() :
:
-
в первой серии он равен
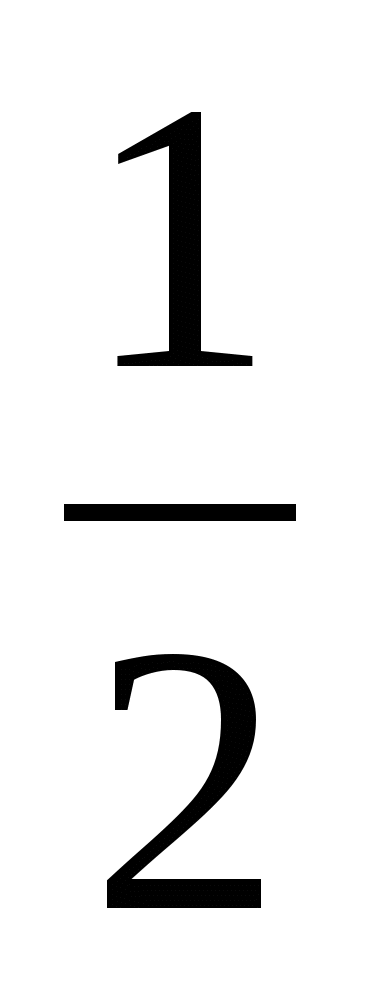 , ибо … 0
, ибо … 0 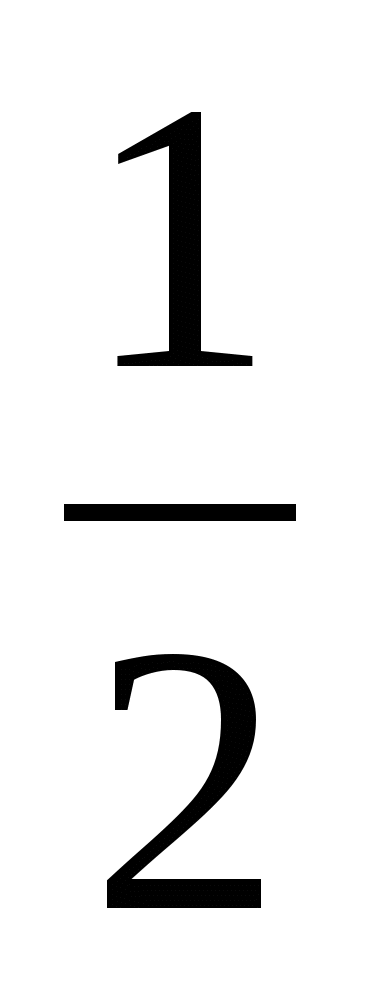
0 1
0 1 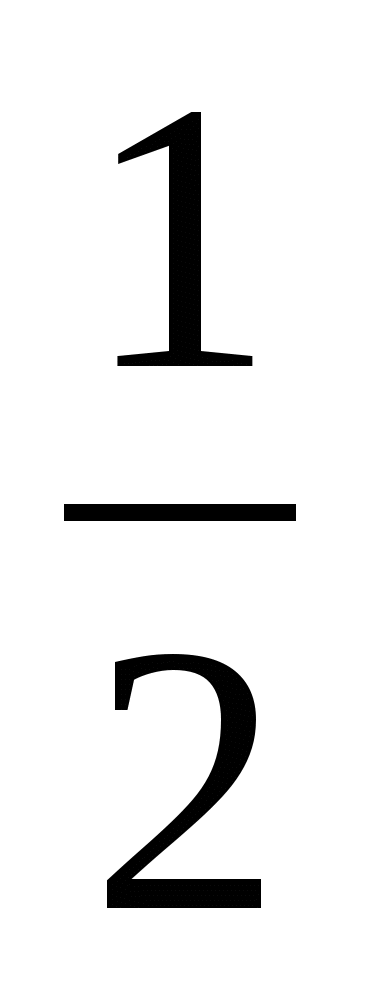 2
2 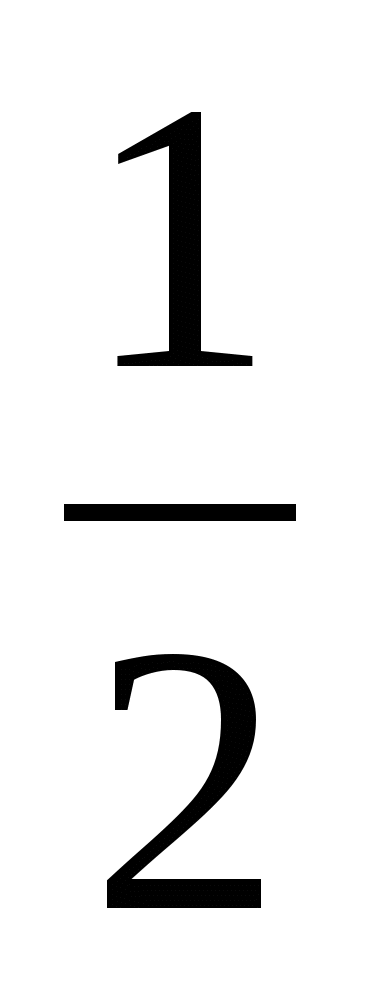 …;
…;
-
во второй серии он равен
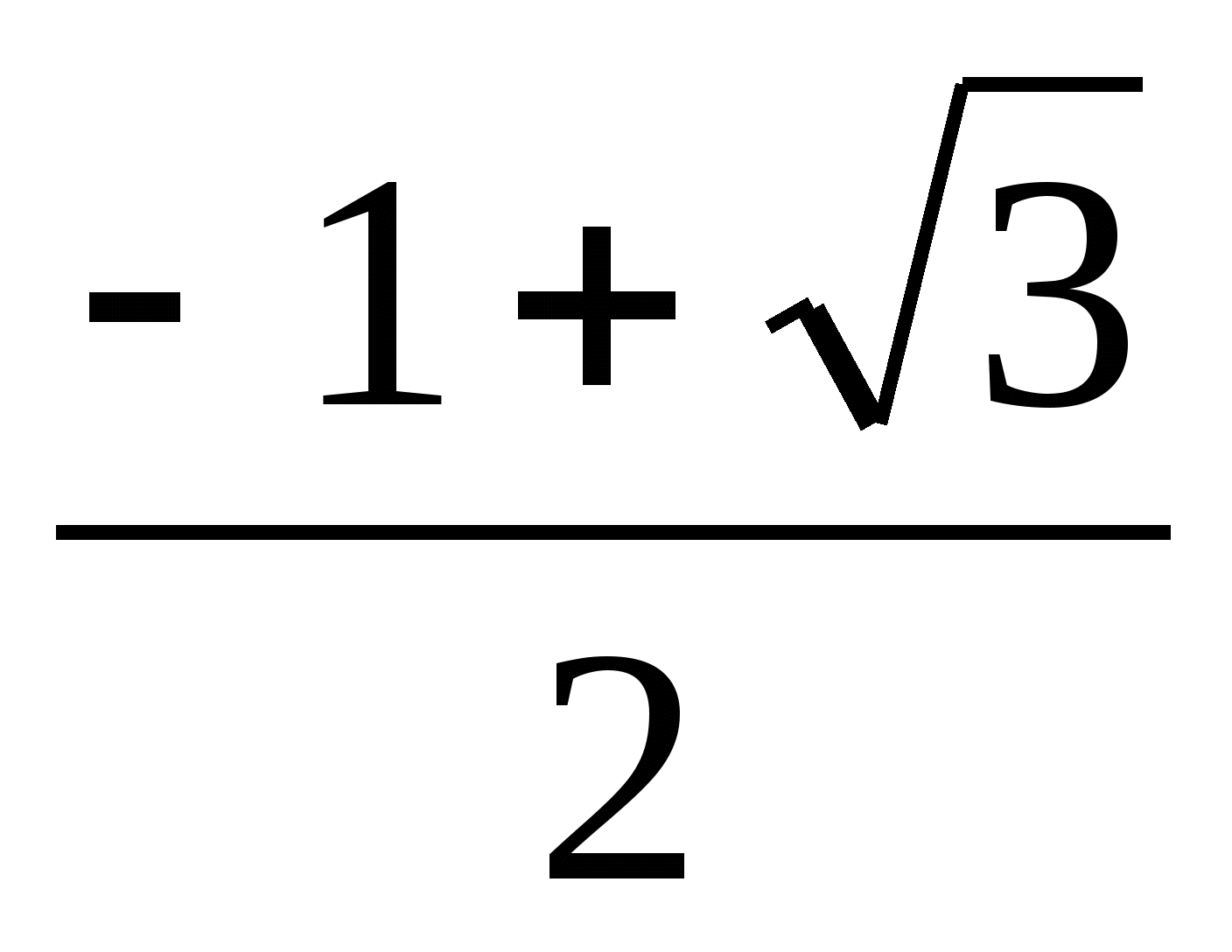
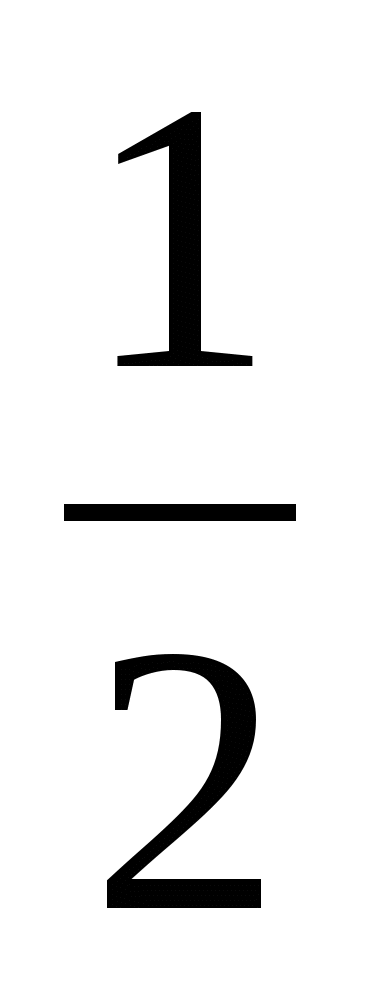 , ибо
, ибо 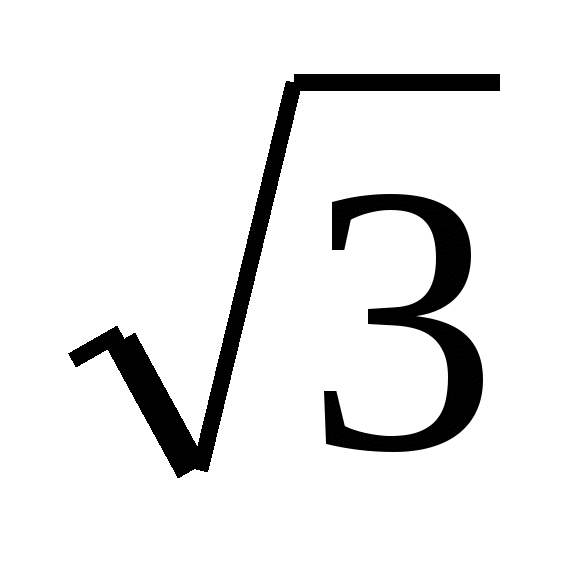 2 и 0
2 и 0 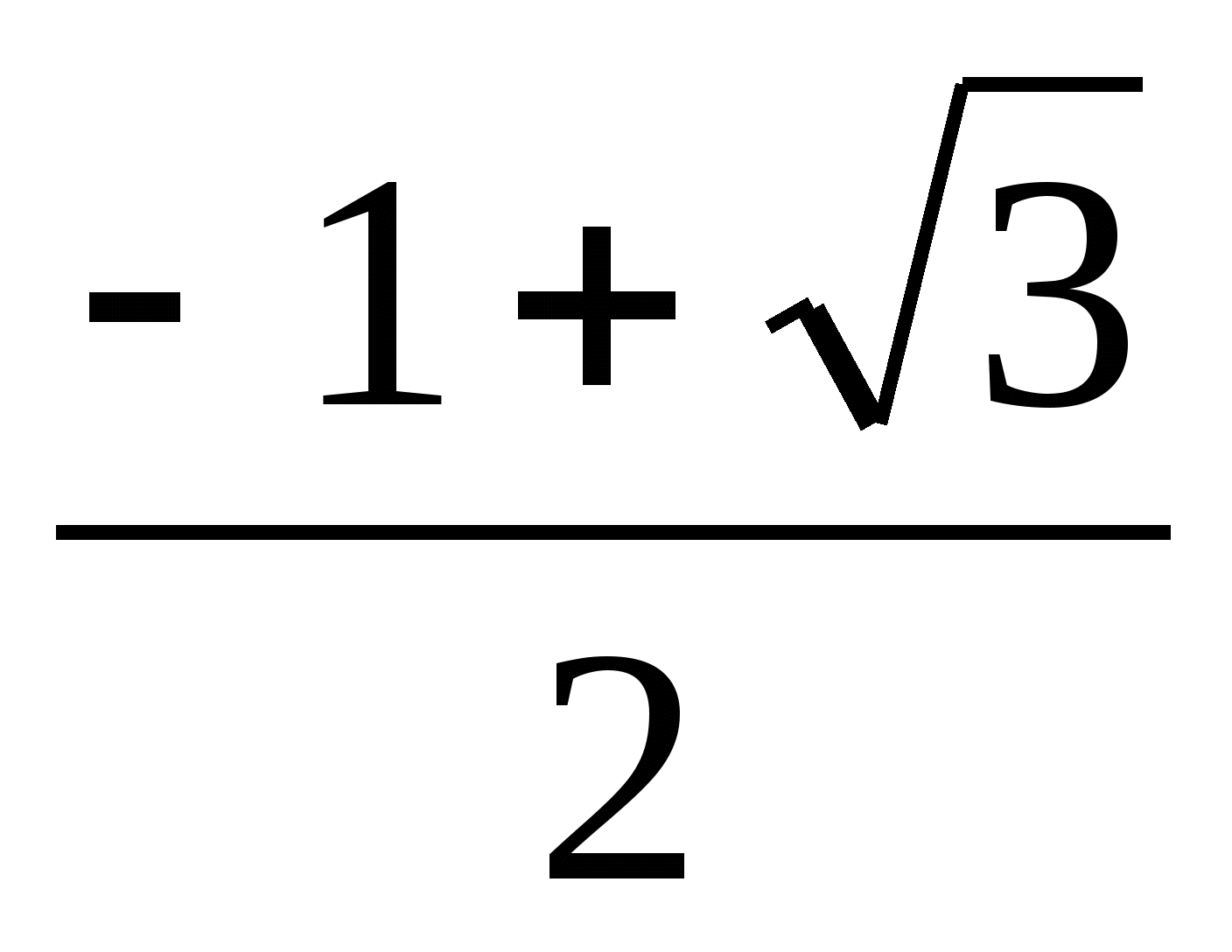
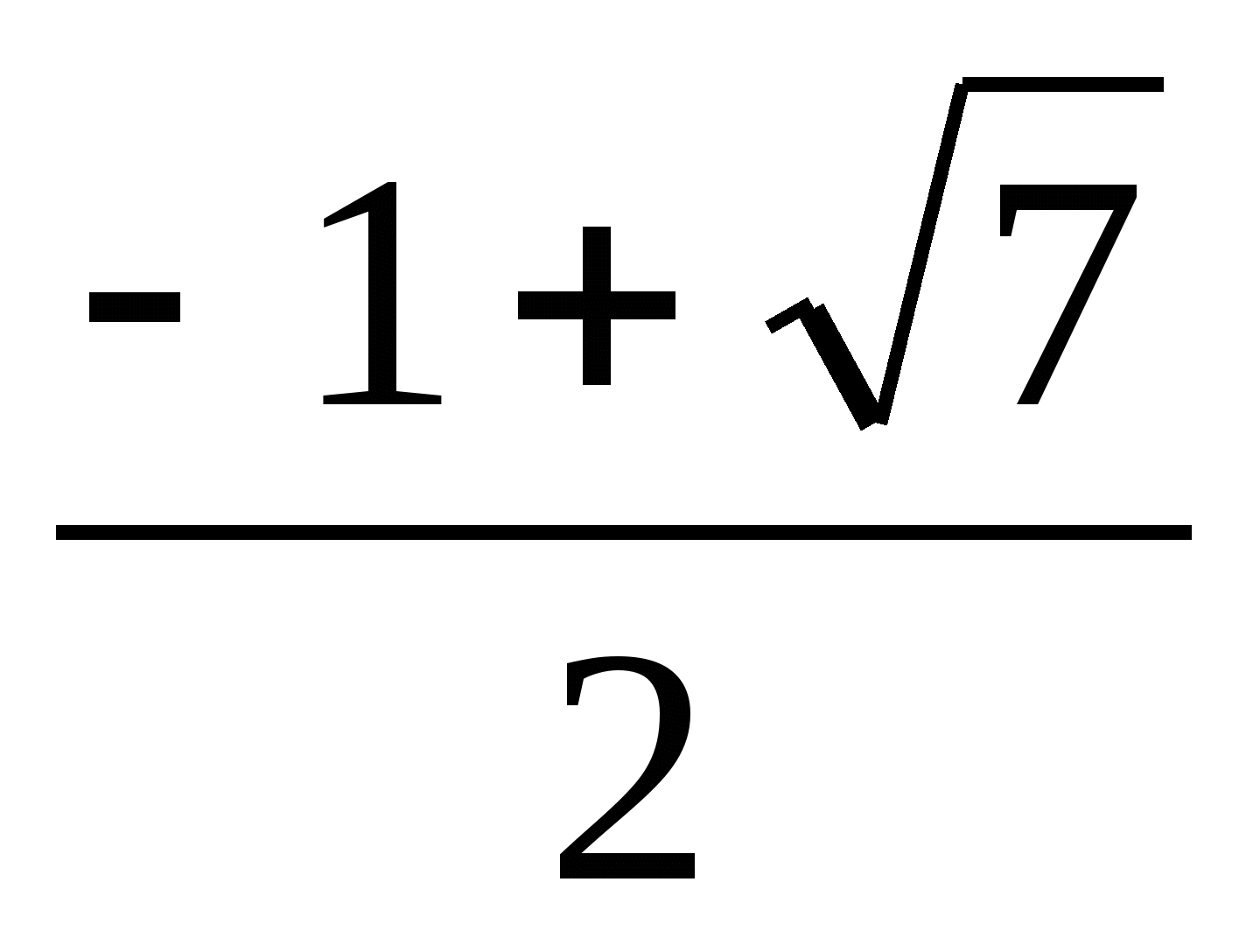 …
…
-
в третьей серии все корни отрицательны.
Ответ: ![]() .
.
Пример 4. Решить уравнение sin 4x = cos (1800 - 2x) и указать его решения, входящие в [-300; 00].
Решение: Воспользуемся формулой приведения, тогда sin 4x = cos 2x,
2sin 2x cos 2x + cos 2x = 0, cos 2x (2sin 2x + 1) = 0.
Отсюда cos 2x = 0 или 2sin 2x + 1 = 0.
Имеем два решения 2х1 = ![]() , nZ, x1 =
, nZ, x1 = ![]() , nZ;
, nZ;
sin 2x2 = ![]() ,
2x2 = (1)k+1
,
2x2 = (1)k+1![]() ,
kZ, x2 = (1)k+1
,
kZ, x2 = (1)k+1![]() ,
kZ.
,
kZ.
Теперь из этих решений предстоит выбрать те, которые лежат в заданном промежутке. Найдем значения х1 и х2 при n = 0, 1 и k =0, 1:
n = 0; x1 = 450; k = 0; x2 = 150;
n = 1; x1 = 450; k = 1; x2 = 750;
n = 1; x1 = 1350; k = 1; x2 = 1050.
На промежутке [300; 00] имеется лишь один корень исходного уровня х =150.
Ответ: х =150.
-
Выполнение упражнений
а) Решить уравнения и найти корни, расположенные на заданных промежутках. Ответ привести в градусах:
cos2x + 3cos x = 0 на отрезке [00; 900];
2sin2 2x - 1 = 0 на промежутке (00; 450).
б) Найти наименьший положительный корень уравнения:
sin (x2) = sin ((x2 + 2x)).
-
Итоги урока
На уроке мы рассмотрели уравнения и научились отбирать корни уравнения используя монотонность корней уравнения вида sin x = a, cos x =a, tg x = a,
ctg x = a. Случаи, когда для отбора требуется умение работать с тригонометрическими неравенствами, рассмотрим на следующем уроке.
6. Домашнее задание