Конспект урока по геометрии (8 класс) на тему 'Теорема Пифагора'

Геометрия, 8 класс

Тема: Теорема Пифагора.

Цель: обобщить и систематизировать знания учащихся по

теме «Теорема Пифагора»;

развивать навыки самостоятельной работы, логическое

мышление, творческие способности учащихся;

воспитывать интерес к изучению математики.

Тип урока: урок обобщения и систематизации знаний.

Оборудование: дидактическая игра «Математическое лото», тестовые задания по готовым рисункам, рисунки к различным способам доказательства теоремы, таблица - дешифратор; картинка - ребус и высказывание А.С. Пушкина о математике, веревка с узелками; числовой код к зашифрованной теме урока.

Ход урока.

1. Организационный момент.

(На доске ряд чисел, расшифровав которые в течение урока, дети назовут тему урока)

90^о; 12/13; 2,4; 5/13; 12/13; 5/12; 45⁰

; 9; 8; 45⁰ ; 13; 2,4; 5/13; 45⁰

1. Сообщение целей, задач урока. Я надеюсь, что сегодняшний урок расширит ваш кругозор и у вас появится стремление к самообразованию.

2. Ребята, кто из вас дома расшифровал ребус?

( Дети отгадывают ребус, учитель обращает внимание учащихся на то, что это высказывание А.С. Пушкина о математике)

«Вдохновение нужно в геометрии, как и в поэзии».

2. Актуализация опорных знаний.

1) «Мозговой штурм».

1. Я - часть плоскости, имею три угла

И сумма их 180⁰ всегда.

Попарно три прямых пересекаясь,

При этом образуют стороны мои. (Треугольник)

2. По-разному всегда я называюсь,

Когда углы иль стороны даны:

Коль остры два угла, а третий прям - зовусь…

(прямоугольным)

3. Этот элемент прямоугольного треугольника на греческом языке означает «натянутая тетива». (Гипотенуза)

4. Как называются все стороны прямоугольного треугольника? (Катеты, гипотенуза)

5. Моих заслуг никто не перечтёт

О том всему известно свету.

Ещё у древних египтян я был в почете,

Мне благодаря и Пифагор стал славен.

Уж так и быть, открою вам секрет:

Квадрат моей гипотенузы

Равен сумме квадратов катетов.

Пусть гипотенуза у меня равна пяти,

Тогда её квадрат есть 25,

А катеты мои - 3 и 4.

Сложи квадраты их, увидишь,

Чудо совершилось:

К шестнадцати прибавив 9, получим 25!

И как же называют все меня? Не долго думая, ответь скорее!

(Египетский треугольник)

6. Как называется наука о тригонометрических функциях? (Тригонометрия)

«Тригон»- треугольник, «метрео»- измеряю (греч), измерение треугольников. Сейчас тригонометрию применяют даже для измерения расстояния между космическими кораблями.

7. С тригонометрией сейчас знакомы даже звери

Все правила расскажут нам четко и уверенно.

Мы попросим всех зверят рассказать их для ребят.

Как же косинус найти ты спроси медузу.

- Делим ПРИЛЕЖАЩИЙ КАТЕТ на гипотенузу.

Синус вычислить сумеет зверь любой из чащи:

На гипотенузу делим КАТЕТ ПРОТИВОЛЕЖАЩИЙ.

Чтобы тангенс получить нужно катеты делить.

Вы в числителе берёте тот, что для угла напротив.

Тот, который прилежит, в знаменателе пиши.

Если дробь перевернуть, это тоже верный путь!

Ты с конца прочти, дружок, как ложится «снег на ток»?

Прочитали? (Котангенс)

8. От чего зависит величина косинуса угла в прямоугольном треугольнике? (Только от градусной меры угла и не зависит от расположения и размеров треугольника).

9. Фамилия этого известного математика состоит из трех слогов: первый слог - число, второй - нота, третий - одно из имён древнеегипетского бога Солнца. (ПИ - ФА - ГОР)

10. О какой теореме идет речь?

Если дан нам треугольник и притом с прямым углом,

То квадрат гипотенузы мы всегда с тобой найдём:

Катеты в квадрат возводим, сумму их легко находим -

И таким простым путём к результату мы прейдем.

(Теорема Пифагора)

2) Учащийся готовится к доказательству теоремы Пифагора. Он у доски выполняет необходимые записи, может использовать заранее подготовленные рисунки к различным способам доказательства теоремы

3) Устный счет (рисунки заранее приготовлены на доске)

1. Градусная мера наибольшего угла в прямоугольном треугольнике. (90^о)

2. Используя рисунок, найдите cos α, tg β, sin α, ctg β:

В

5м β 13м

С α А

12 м

(cos α = ; tg β = = 2,4; sin α = ; ctg β = )

3. Градусная мера острого угла в прямоугольном равнобедренном треугольнике (45^о)

4. Диагональ квадрата, сторона которого 1 м. (x= м)

Используя рисунок, найдите неизвестный элемент х

5.

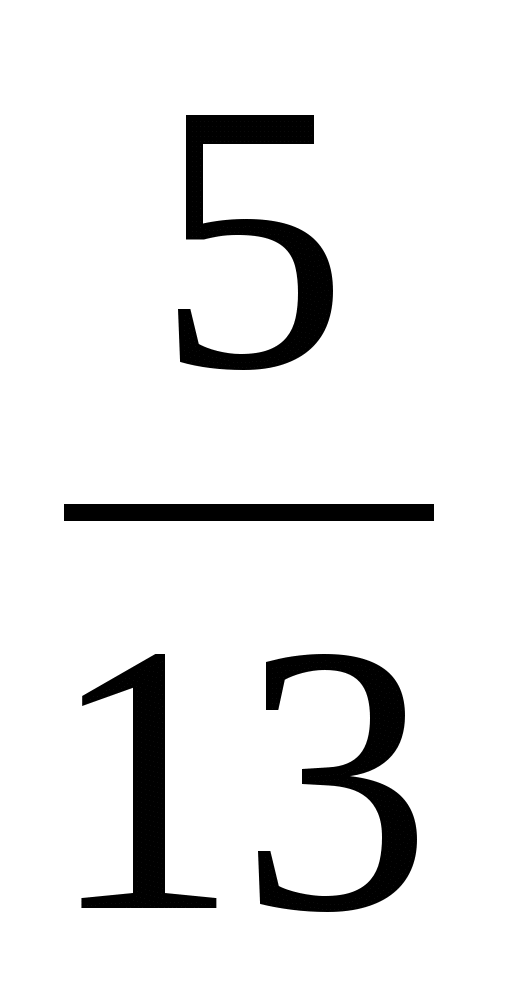
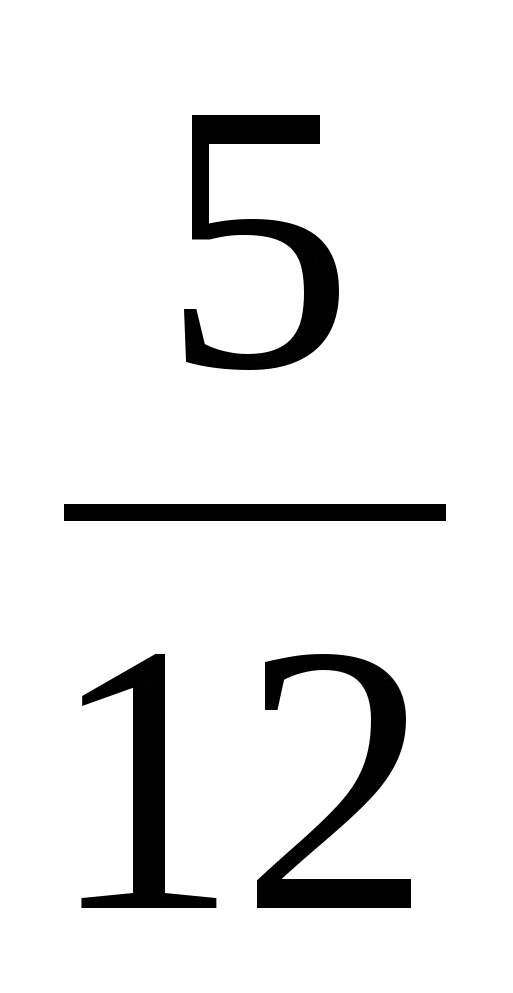
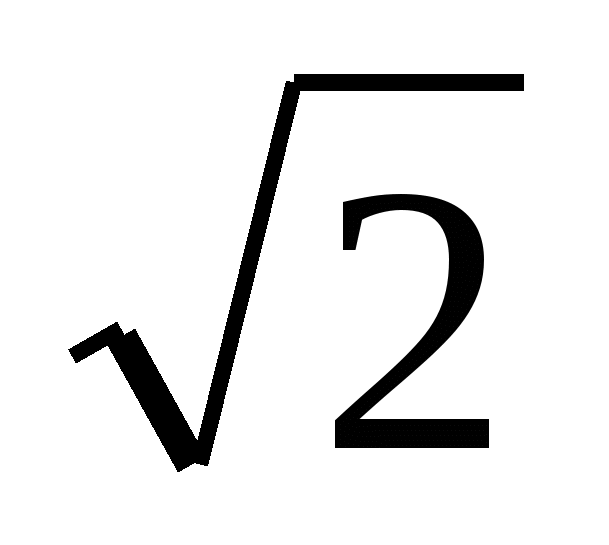
x 15 м (x= 9 м)

12 м

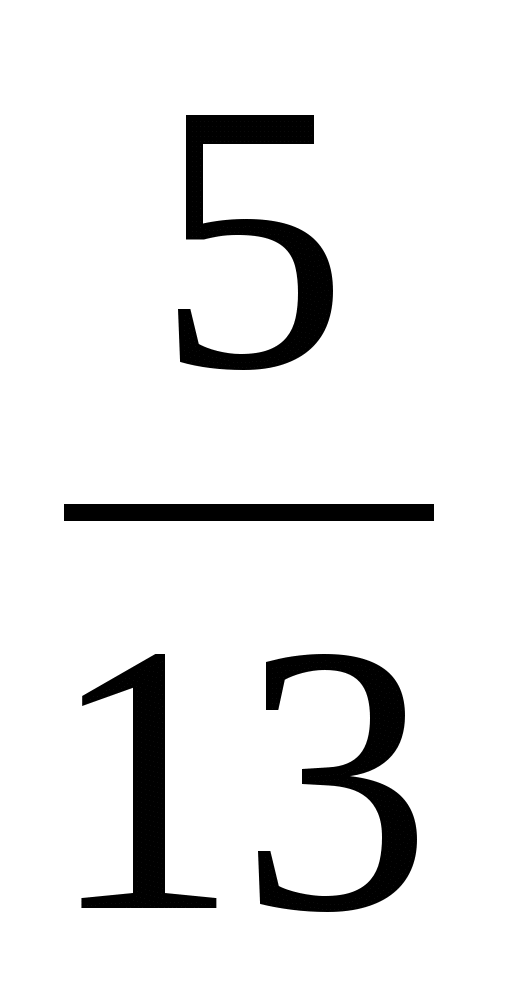
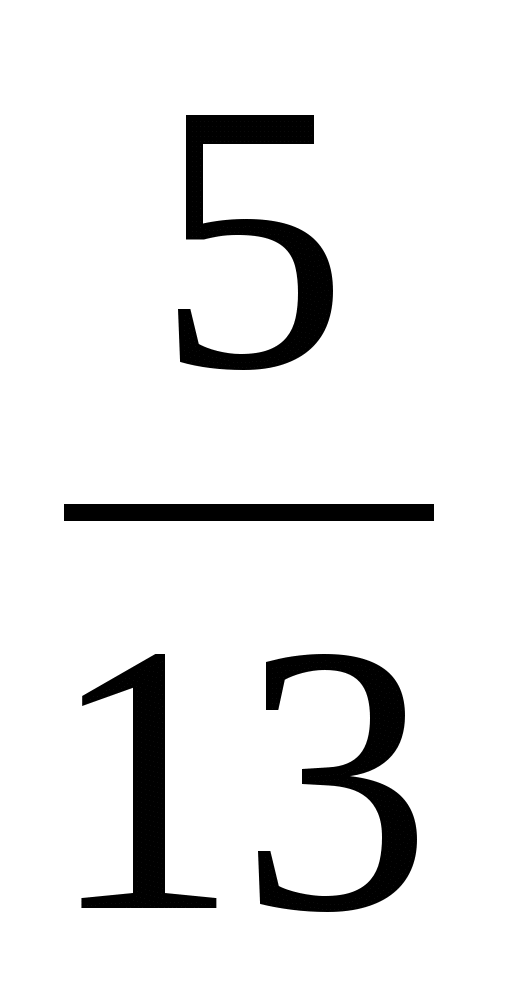6. 10 м

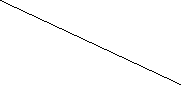
х 10 м (х = 8 м)

16 м

7. В ромбе диагонали 24 м и 10 м. Чему равна его сторона?

(13 м)

4) Тема урока

Ребята, обратите внимание на доску.

Здесь вы видите ответы к только что решенным задачам. Расшифруйте тему нашего урока, которая спряталась под числовым кодом, используя таблицу- дешифратор.

Ученики называют тему урока, записывают ее в тетрадь, а учитель пишет ее на доске. (Таблица-дешифратор прилагается)

5) Доказательство теоремы Пифагора (ответ ученика).

III. Блиц-опрос по формулам.

Игра «Математическое лото» прилагается.

IV. Блиц - конкурс «А ЗНАЕТЕ ЛИ ВЫ, ЧТО…» Домашнее задание. Ответы учащиеся показывают с помощью карточек с цифрами.

1. Многих учёных можно назвать долгожителями. Каждый из них прожил более 70 лет: 80 лет - Платон, 88 лет - Гаусс, около 100 лет - Фалес, а сколько лет жил Пифагор?

1) 75, 2) 85, 3) 90, 4) 105 лет.

2. По результатам исследований четверо учёных - математиков имели свои школы:

   1. у Фалеса философская школа в Милете;

   2. у Пифагора - «ПИФАГОРЕЙСКИЙ СОЮЗ» в Кротоне;

   3. у Платона - «Академия» - философская школа в Афинах;

   4. у Евклида - школа в Александрии.

В Уставе какой школы говорилось:

«Беречь тайну учения своего учителя?».

3. Часть членов Пифагорейского союза называли математиками, а часть - акузматиками. Кого в этом союзе называли АКУЗМАТИКАМИ?

   1. тех, кто не знал математику;

   2. тех, кто знал математику и передавал свои знания другим;

   3. тех, кто придерживался идеалистических взглядов и строго берёг тайну учения своего учителя;

   4. учащихся с материалистическими взглядами.

4. В девятом томе полного собрания сочинений Ивана Франка /всего 50 томов/

помещены, выполненные им переводы поэтических сочинений известных математиков и философов античного мира. В этом томе нет работ:

1. Платона; 2) Пифагора; 3) Архимеда; 4) Евклида?

5. Решение задач.

1. Презентация домашнего задания «СТАРИННЫЕ ЗАДАЧИ, РЕШАЕМЫЕ С ПОМОЩЬЮ ТЕОРЕМЫ ПИФАГОРА».

I группа.

В древности задачи составляли в стихотворной форме, чтоб легко запоминались.

Над озером тихим с полфута размером,

Высился ЛОТОСА цвет.

Он рос одиноко, а ветер

Порывом отнес его в сторону.

Нет больше цветка над водою.

Нашел же рыбак его ранней весною

В двух футах от места, где рос.

Итак, предложу я вопрос: «Как глубоко озеро это?»

Пояснения к решению.

(x+ )²=x²+2² , .

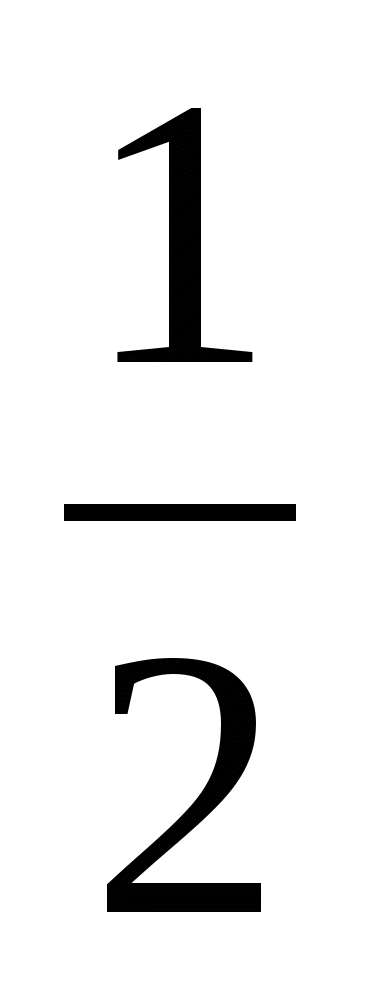x²+x+=x²+4 , 2

х

x=4

Ответ: глубина озера 4 фунта.

II группа.

В одном из самых ранних вавилонских математических текстов, относящимся к XVIII- XIX векам до н. э. содержится следующая изящная задача.

Палка длиной прислонена к стене. Её верхний конец опустили на .

Как далеко отодвинется её нижний конец?

Пояснения к решению.

-==

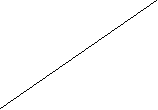
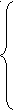
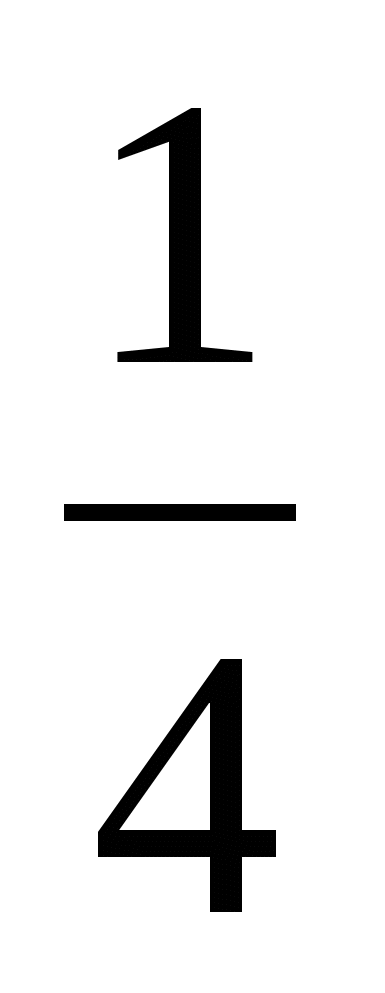
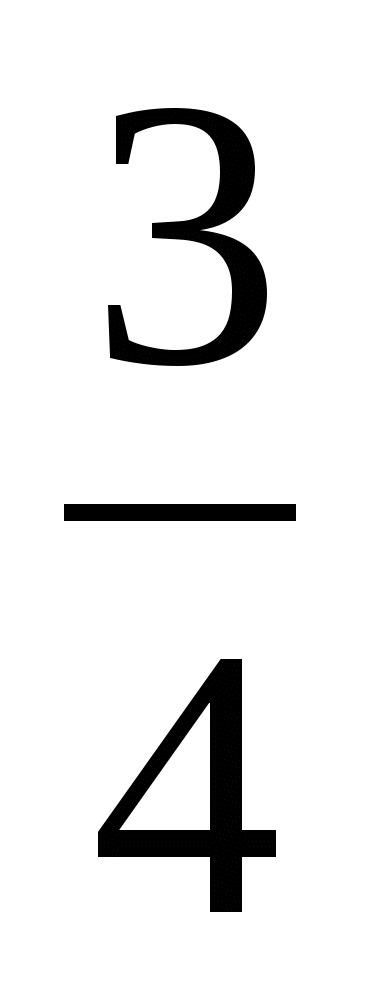
a== 0,3

III группа.

На Руси в рукописных изданиях начала XVII века есть задача, которую решали с помощью теоремы Пифагора.

Хошь узнати, что будет промежь монастырями, не ходя и не меревь? Тогда познавай: как ходил будто к Троице в Сергиев монастырь, и тут 32 версты; ходил же в Воскресный монастырь, и тут будто 24 версты. Что будет промежь теми монастырями, скажи, не меревь.

Пояснения к решению.

Другими словами надо найти расстояние между монастырями с учетом того, что автор считает, что находится в вершине прямоугольного треугольника, катеты которого 24 версты и 32 версты. Тогда расстояние между монастырями 40 верст.

IV группа.

У одного арабского математика XI века находим следующую задачу:

На обоих берегах реки растет по пальме, одна против другой. Высота одной - 30 локтей, другой - 20 локтей; расстояние между их основаними - 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую на поверхность воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?

Пояснение к рещению.

АВ=АС, т.к. обе птицы пролетели эти расстояния за одинаковое время.

30²+x²=20²+(50-x)² В

1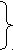00x=2000 С

x=20.

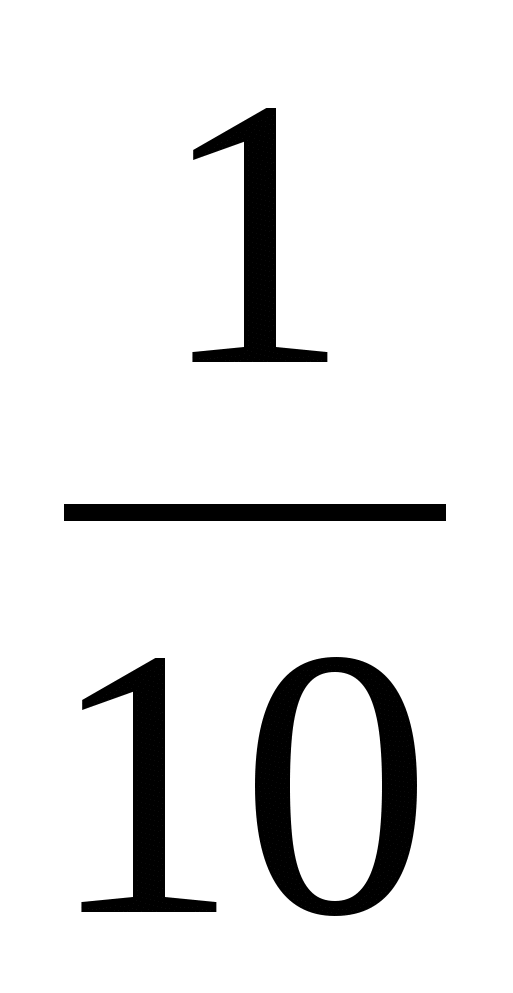
Рыба появилась в 20 локтях от той пальмы, А

высота которой 30 локтей.

2. Работа в новых группах:

ПРАКТИКИ, СПЕЦИАЛИСТЫ И МЫСЛИТЕЛИ.

«Практики» и «Специалисты» работают самостоятельно, а «Мыслители» с учителем.

• КАРТОЧКА - ЗАДАНИЕ ДЛЯ «ПРАКТИКОВ»

1. Как в древности строили прямой угол?

У детей на столе верёвка с узелками.

2. Как получить прямоугольный треугольник из одной целой спички? (Спичку надо положить в углу крышки стола.)

• Самостоятельная работа «СПЕЦИАЛИСТОВ»

(в виде тестов на два варианта)

• «МЫСЛИТЕЛИ» работают с учителем

Тропинка к истине сложна

И потому в мышленье чистом

Отвага дерзкая нужна

Не меньше вам, чем альпинистам.

Евклид в первой книге «Начал» сформулировал теорему Пифагора так:

В прямоугольном треугольнике квадрат на стороне, которая стягивает прямой угол, равен вместе взятым квадратам на сторонах, образующих прямой угол.

Как можно сформулировать теорему Пифагора, используя понятие площади?

Для любого прямоугольного треугольника площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Применим эту формулировку для решения задачи.

Задача.

Разность площадей квадратов, построенных на катетах прямоугольного треугольника, равна 119 см² Найдите периметр треугольника, если площадь квадрата, построенного на гипотенузе, равна 169 см² . (Р = 30 см)

После того, как «Мыслители» решат свою задачу, «Специалисты» прекращают работу. Все слушают «Практиков». Если останется время, учащиеся рассказывают о различных названиях теоремы Пифагора:

«ОСЛИННЫЙ МОСТ» или «БЕГСТВО УБОГИХ;

«ГЕКАТОМБА», «ТЕОРЕМА НИМФЫ, РУСАЛКИ»;

«МАГИСТР МАТЕМАТИКИ».

VI. ИТОГ УРОКА.

- В чём же причина популярности теоремы Пифагора?

Знатоки утверждают, существует три причины: ПРОСТОТА, КРАСОТА, ШИРОЧАЙШАЯ ПРИМЕНИМОСТЬ.

- Что нового вы узнали?

- Понравился урок?

Комментируются оценки наиболее активным учащимся. Все дети сдают тетради в конце урока.

VII. ДОМАШНЕЕ ЗАДАНИЕ.

Каждый ученик получает домашнее задание на карточке. Задание прилагается.

Пусть ты не станешь Пифагором

Каким хотелось, может быть!

А будешь ты рабочим иль ученым

И будешь честно Родине служить.

ПРИЛОЖЕНИЕ 1.

1. Домашнее задание:

• повторить теоретический материал по теме, подготовиться к контрольной работе;

• решить

ЗАДАЧУ ДРЕВНЕИНДИЙСКОГО УЧЕНОГО БХАСКАРЫ

Н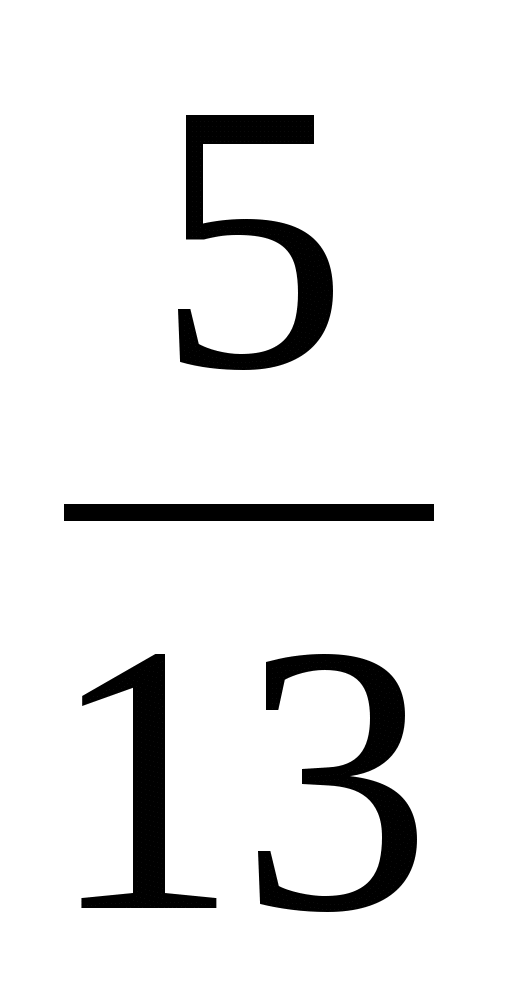а берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломил

И бедный тополь упал, но угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в том месте река

В четыре лишь фута была широка.

Верхушка склонилась у края реки,

Осталось три фута всего у ствола.

Прошу вас, скорее теперь мне скажите:

Как у тополя велика высота?

ПРИЛОЖЕНИЕ 2. Таблица - дешифратор.

А

Г

Е

И

М

45⁰

13

12/13

9

5/12

О

П

Р

Т

Ф

2,4

5/13

90⁰

8

ПРИЛОЖЕНИЕ 3. Тестовые задания по готовым рисункам

для группы «Специалистов»

Вариант 1

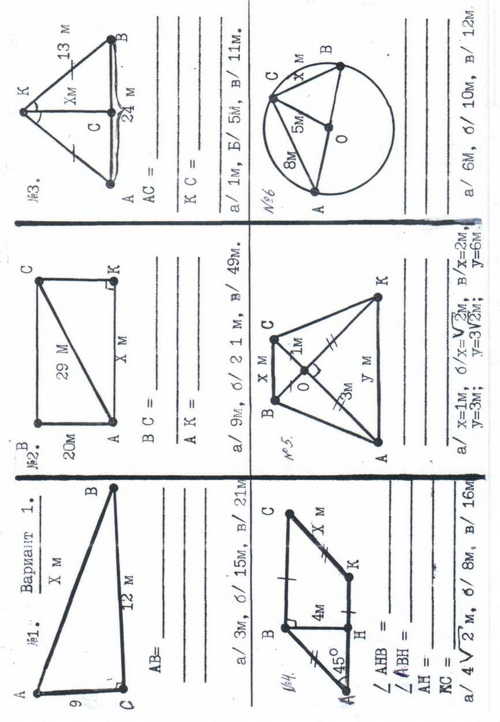
Вариант 2

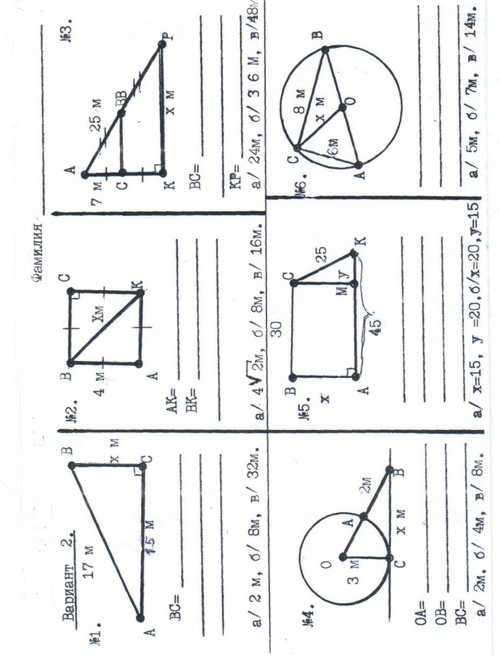
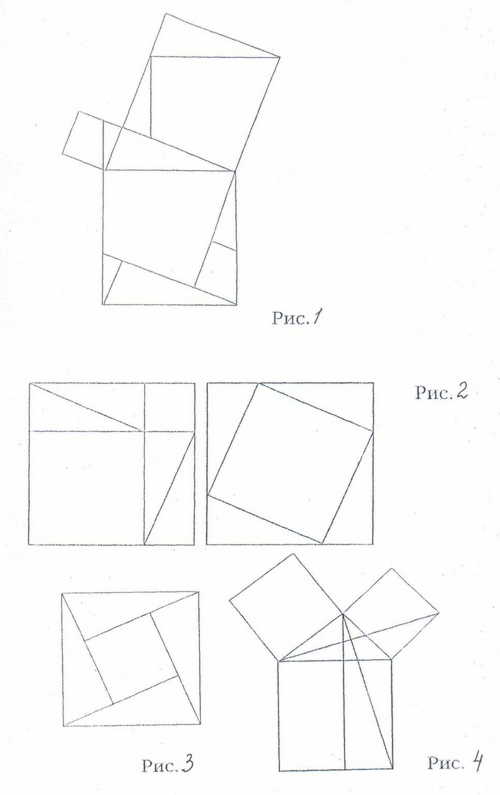
ПРИЛОЖЕНИЕ 4.

Рисунки к доказательствам теоремы Пифагора.

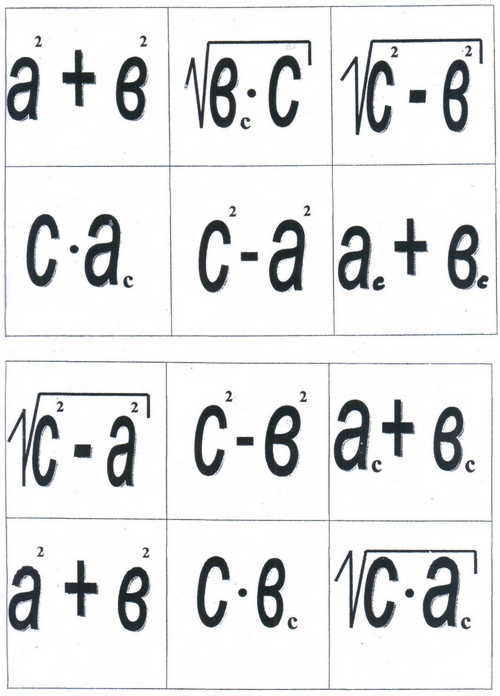
ПРИЛОЖЕНИЕ 5. Дидактическая игра «Математическое лото»

Вариант 1 Теорема Пифагора

а

в

с ²

с

в ²

а ²

Вариант 2 Теорема Пифагора

с

а ²

в

а

в ²

с ²

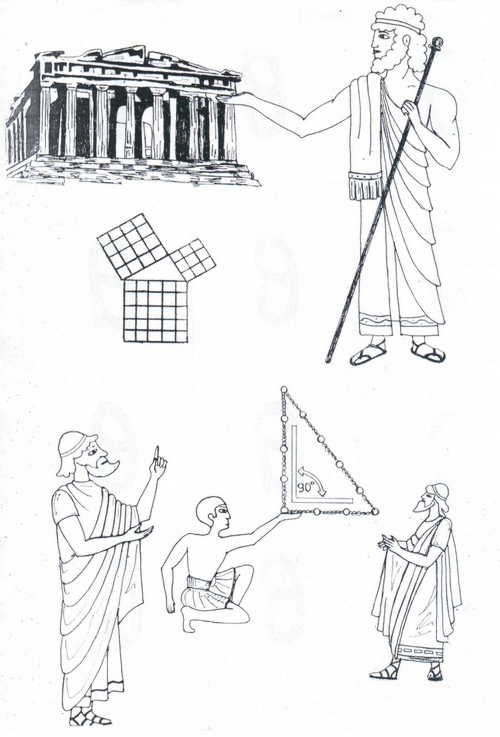
ПРИЛОЖЕНИЕ 6.

Ребус с высказыванием А.С.Пушкина о математике.

«Вдохновение нужно в геометрии, как и в поэзии».

ПРИЛОЖЕНИЕ 7. Задания для группы «Практиков»

1. Как в древности строили прямой угол?

У детей на столе верёвка с узелками.

2. Как получить прямоугольный треугольник из одной целой спички? (Спичку надо положить в углу крышки стола.)

Домашнее задание группам к обобщающему уроку по теме

«Теорема Пифагора»

1. Расшифруйте ребус - высказывание А.С. Пушкина о геометрии.

(ребус прилагается)

2. «Мозговой штурм».

Подберите по 2-3 вопроса по изучаемой теме, ответ должен быть чётким, кратким.

3. Подготовьте сообщение на 1-2 минуты по теме

«Как называли теорему Пифагора в древние века?»

4. Конкурс «А знаете ли вы?»

Подготовьте по 1 вопросу в виде теста занимательного характера.

5. Найдите и решите старинную задачу с помощью теоремы Пифагора (нарисуйте к ней рисунок и решение подготовьте на альбомном листе).

5. Историческая справка (каждой группе отдельный вопрос):

I группа: Биография Пифагора.

II группа: О пифагорейском союзе.

III группа: «Пифагор - олимпиец».

IV группа: «Устами Пифагора».