- Учителю
- Урок алгебры в 7 классе по теме «Статистические характеристики»
Урок алгебры в 7 классе по теме «Статистические характеристики»
Урок алгебры в 7 классе
Тема: Статистические характеристики.
«Кто владеет информацией, тот правит миром»
Ф. Бекон
Цели урока:
-
Ввести понятие статистических характеристик (среднего арифметического, моды, размаха)
-
Развивать умения находить статистические характеристики, совершенствовать навыки устного счета.
-
Овладевать системой знаний об обществе; формировать логическое, абстрактное, системное мышление; формировать экономически осознанное отношение к окружающему миру.
Задачи урока:
-
Научить определять среднее арифметическое, моду и размах числового ряда.
-
Расширить и углубить знания по предмету, через новые понятия.
-
Воспитывать уважение к мнению других, умение слушать и рассуждать.
Оборудование урока: проектор, компьютер, экран для демонстрации презентации.
Используемые технологии:
Технология на основе личностной ориентации педагогического процесса (преподавание математики как предмета формирующего личность), информационно-коммуникационные технологии (учебная презентация). Для мотивации учащихся на уроках использую «компетентные задачи».
Методы обучения:
1) объяснительно - иллюстративный, или репродуктивный (работа с дополнительными источниками, демонстрация презентации);
2) проблемный (решение проблемных задач).
3) частично-поисковый (использование практических задач в изучении темы)
Ход урока
-
Устный счет.
Ни костяшек, ни ручек, ни мела
- Устный счет. Мы творим это дело
Только силой ума и души!
Числа сходятся где-то во тьме,
И глаза начинают светиться!
И кругом только умные лица.
Устный счет! Мы считаем в уме.
Вычислите:
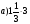 ;
; 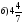 :4;
:4; 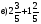 ;
; 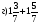 ;
; 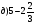 ;
; 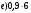 ;
; 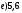 : 7;
: 7;
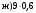 ;
; 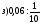 ;
; 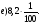
-
Сообщение темы целей, задач урока и мотивация учебной деятельности.
- Доброе утро, ребята! Вы замечательно справились с работой на прошлом уроке, и я уверена, что сегодняшний урок и последующие принесут нам новые открытия и много радости от общения друг с другом. Сегодня мы вспомним то, с чем познакомились в шестом классе и конечно узнаем много нового.
В век бесконечного потока информации крылатое выражение Ф. Бекона приобретает особый смысл. Мало владеть какой-то информацией, её нужно правильно использовать. Но часто информация трудна для восприятия: она не наглядна, занимает много места, никак не упорядочена и т.д. А значит, она не может принести пользу. Единственный разумный выход - преобразовать первоначальную информацию. Значительную часть подобного преобразования берёт на себя статистика.
3. Подготовка к изучению нового материала через актуализацию опорных знаний.
1 этап. Вхождение в урок:
- На перемене на доске каждый обучающийся записывал время, которое он тратит на приготовление домашнего задания по алгебре.
- Высчитаем среднее время (повторить алгоритм нахождения среднего арифметического);
- найдем разницу между самым маленьким и самым большим числом.
- Какое число повторяется несколько раз?
- А зачем все это нужно? Что это дает учителю, учащимся?
2 этап. Ознакомление с новым материалом.
Слово учителя.
- В математике есть раздел «Элементы логики, комбинаторики, статистики и теории вероятностей». Мы уже встречались с решением логических и комбинаторных задач. Сегодня пришло время познакомиться со статистическими характеристиками.
Наша задача узнать, что такое статистика, размах, мода. Научиться применять эти характеристики при анализе ряда данных.
Статистика - наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово "статистика" происходит от латинского слова status, которое означает "состояние, положение вещей". Результаты статистических исследований широко используют для практических и научных выводов.
Затем предложить учащимся для обсуждения следующий пример:
В школе сдавали зачёт по математике. На зачёт пришли 10 человек, и они получили оценки: 5; 3; 4; 4; 5; 3; 4; 5; 2; 4. Как в целом сдали ребята? Какую оценку получали чаще всего? Насколько разными были оценки? (ребята высказывают свое мнение)
Помочь нам в статистическом анализе ряда числовых данных, призваны статистические характеристики:
характеристики среднего, описывающие положение всего числового ряда в целом на числовой прямой;
характеристики разброса, показывающие, насколько значения ряда различаются между собой, как сильно они разбросаны, рассеяны вокруг средних.
К характеристикам среднего относятся:
среднее арифметическое;
мода;
медиана.
К характеристикам разброса относятся:
размах;
дисперсия;
стандартное отклонение.
С помощью учащихся, опираясь на рассмотренный пример, ввести понятия трёх статистических характеристик.
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на их количество.
Медианой упорядоченного ряда чисел с нечетным числом членов называется такое число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Модой называют число ряда, которое встречается в этом ряду наиболее часто.
Моды у ряда может вообще не быть или быть несколько мод.
Размах - это разность наибольшего и наименьшего значений ряда данных.
С остальными статистическими характеристиками познакомимся на факультативном занятии.
Замечание:
Обратить внимание учащихся на важное обстоятельство: медиана практически не чувствительна к значительным отклонениям отдельных крайних значений наборов чисел. В статистике это свойство называется устойчивостью. Устойчивость статистического показателя - очень важное свойство, оно страхует нас от случайных ошибок и отдельных недостоверных данных.
-
Упражнения
Необходимо, чтобы учащиеся четко мотивировали свои ответы.
а) Сложили все члены ряда и полученную сумму разделили на их количество. Значит, искали среднее арифметическое.
б) Нашли разность между наибольшим и наименьшим числом в ряду, то есть размах.
в) Число … встречается наибольшее количество раз, значит, это мода ряда.
г) Составим из данных чисел упорядоченный ряд. В полученном упорядоченном ряду … чисел. В середине ряда находится число … , которое является медианой. (В этом числовом ряду четное число членов, и имеются два числа, расположенные в середине ряда. Найдем среднее арифметическое этих чисел, значит, это медиана ряда.)
-
№ 167.
Найдите среднее арифметическое и размах ряда чисел:
а) 24, 22, 27, 20, 16, 31;
б) 30, 5, 23, 5, 28, 30.
-
№ 168.
Найдите среднее арифметическое, размах, моду и медиану ряда чисел:
а) 32, 26, 18, 26, 15, 21, 26;
в) 67,1, 68,2, 67,1, 70,4, 68,2.
-
№ 169.
Найдите среднее арифметическое, размах и моду ряда чисел:
а) 16, 22, 16, 13, 20, 17;
в) -21, -33, -35, -19, -20, -22.
-
№ 170.
Как могут измениться размах и мода ряда чисел, если:
а) дополнить его числом, превосходящим все остальные;
б) вычеркнуть из него число, меньшее остальных;
в) дополнить его числом, равным наибольшему из чисел?
-
№ 171.
В таблице показан расход электроэнергии некоторой семьей в течение года:
Месяц
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII
Расход электроэнергии, кВт ч
ч
85
80
74
61
54
34
32
32
62
78
81
82
Найдите средний ежемесячный расход электроэнергии этой семьей.
-
Задача.
Найдите для числового ряда
1, 2, 3, 4, х
Все возможные значения х, при которых:
а) среднее арифметическое ряда равняется 3;
б) мода равняется 3;
в) медиана равняется 3.
Решение
а) 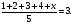
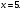
б) Мода будет равняться 3, если х = 3. В других случаях ее либо не будет, либо она будет равна другому числу.
в) Медиана будет равняться 3 при всех 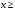 3. При х < она будет меньше 3.
3. При х < она будет меньше 3.
№ 173.
Среднее арифметическое ряда, состоящего из десяти чисел, равно 15. К этому ряду приписали число 37. Чему равно среднее арифметическое нового ряда чисел?
№ 175.
В ряду 2, 7, 10, , 18, 19, 27 одно число оказалось стертым. Восстановите его, зная, что среднее арифметическое этих чисел равно 14.
№ 179.
В аттестате о среднем образовании у четырех друзей - выпускников школы - оказались следующие оценки:
Ильин: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;
Семенов: 3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4;
Попов: 5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4;
Романов: 3, 3, 4, 4, 4, 4, 4, 3, 4, 4. 4, 5, 3, 4, 4.
С каким средним баллом окончил школу каждый из этих выпускников? Укажите наиболее типичную для каждого из них оценку в аттестате. Какие статистические характеристики вы использовали при ответе?
№ 181.
Проведя учет бракованных деталей в 10 ящиках с одинаковым числом деталей, получили следующий ряд данных:
1, 2, 2, 3, 1, 0, 2, 1, 3, 2.
Найдите для этого ряда среднее арифметическое, размах и моду. Что характеризует каждый из этих показателей?
-
Самостоятельная работа
1. Найти среднее арифметическое ряда: 1,6; 4,9; 12,4; 3,1.
2. Найти моду ряда: 13; 15; 13; 12; 12; 12; 13; 14; 13; 15; 13;
3. Найти медиану: 39; 54; 33; 36; 20; 29; 35; 50; 21.
4. Найти размах ряда:
а) 12; 25; 38;
б) 7,2; -0,6; -4,5; 6,3; 1,1.
Ответы:
-
5,5.
-
13.
-
35.
-
а) 26;
б) 11, 7.
6. Итоги урока.
- Какие существуют средние статистические характеристики ряда?
- Какой ряд называется упорядоченным?
- Что называется размахом ряда? Приведите пример.
- Что такое мода ряда? Приведите пример.
- Как найти среднее арифметическое ряда?
-
Задание на дом: составить кроссворд по теме «Статистика»