- Учителю
- Конспект урока по геометрии на тему 'Признаки равенства треугольников' (7 класс)
Конспект урока по геометрии на тему 'Признаки равенства треугольников' (7 класс)




МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ЛИДИНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
143118, Московская область, т./факс 8- (49627 )-66-310
Рузский район,д. Лидино, д. 8б E mail lidino-school@ yanlex/ru


Предмет: геометрия.
Класс: 7.
« Признаки равенства треугольников. Решение задач»
![]() урок комплексного применения знаний, умений и навыков.
урок комплексного применения знаний, умений и навыков.
![]()
Образовательные: формирование умений применять признаки равенства треугольников для решения задач, распознавать равные треугольники, делать вывод о равенстве треугольников, применяя теоремы .
Воспитательные: формирование навыков самоконтроля; мыслительной активности.
Развивающие: развитие творческих способностей, познавательной активности, интереса к предмету, пространственного воображения и логического мышления учащихся.
ОБОРУДОВАНИЕ: компьютер, интерактивная доска, бланки, математическое лото.
План урока:
-
а) Организационный момент.
б) Проверка домашнего задания
-
Устная работа
-
Работа с бланками.
-
Игра «Математическое лото»
-
Подведение итогов урока. Историческая справка.
-
Итог урока. Задание на дом.
Ход урока.
I. Мы изучили три признака равенства треугольников, узнали все свойства равнобедренного треугольника.
Сегодня мы продолжаем учиться использовать их для решения задач. Урок будет немного необычным, поэтому прошу положить свои письменные принадлежности и учебники на край парты.
Начнём урок с проверки домашнего задания.
Нужно доказать два утверждения:
-
В равных треугольниках медианы , проведенные к равным сторонам . равны.
-
В равных треугольниках биссектрисы равных углов равны.( у доски два человека)
Класс работает устно(работа с сигнальными карточками: зелёная - верно, оранжевая - ложно).(Вопросы подготовлены на интерактивной доске)
-
Два треугольника равны, если три угла одного треугольника равны трём углам другого треугольника.(л)
-
Два треугольника равны, если сторона и два прилежащих к ней угла, одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника(в)
-
Медиана это перпендикуляр, проведённый к противоположной стороне(л)
-
Биссектриса это отрезок, проведённый к противоположной стороне и делящей угол пополам (в)
-
Если сторона и два прилежащих к ней угла одного треугольника, соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны (в)
-
В равнобедренном треугольнике все стороны равны.(Л)
-
Треугольники равны, если три стороны одного треугольника соответственно равны трём сторонам другого треугольника.(в)
-
Высота это перпендикуляр, проведённый из вершины к противолежащей стороне треугольника (в)
II. А теперь мы будем по готовым чертежам решать задачи устно.(интерактивная доска)
-
Чему равен отрезок ДС?
-
Дано: угол АВС=120° Найти угол М.
-
Дано: угол CRM=30° Найти: угол СКМ.
-
Найти: FK
Физминутка .
III. Работа с бланками (наличие у каждого и проверка на интерактивной доске)
1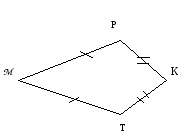 . На рисунке МР=МT РК=TК. Какие точки достаточно соединить, чтобы получились равные треугольники?
. На рисунке МР=МT РК=TК. Какие точки достаточно соединить, чтобы получились равные треугольники?
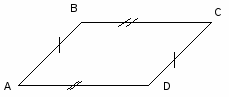
2. Какие точки достаточно соединить, чтобы получились равные треугольники?
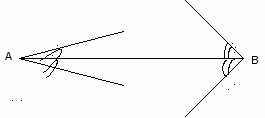
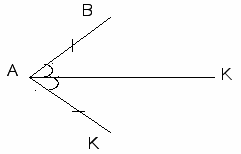
3. Отрезок АВ делит пополам каждый из двух углов ![]() А и
А и ![]() В. Закончите чертёж, чтобы получились равные треугольники. Назовите хотя бы одну пару получившихся равных отрезков.
В. Закончите чертёж, чтобы получились равные треугольники. Назовите хотя бы одну пару получившихся равных отрезков.
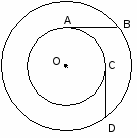
4. На рисунке даны две окружности с общим центром О и равные отрезки АВ и СД. Какие пары точек достаточно соединить , чтобы получились равные треугольники? Начертите их.
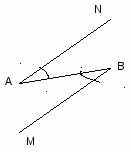
5. Из концов отрезка АВ провели лучи AN и BM так, чтобы ![]() NAB =
NAB = ![]() MBA. Проведите прямую так, чтобы на чертеже появились равные треугольники.
MBA. Проведите прямую так, чтобы на чертеже появились равные треугольники.
6.
1. Проведите отрезок так, чтобы получились равные треугольники.
2. Проведите два отрезка так, чтобы получились равные треугольники.
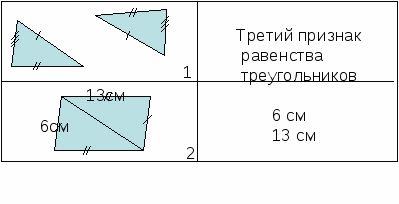
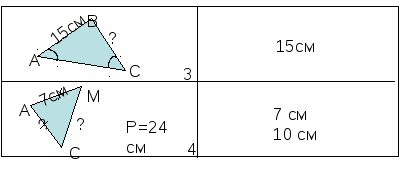
IV. Математическое лото.



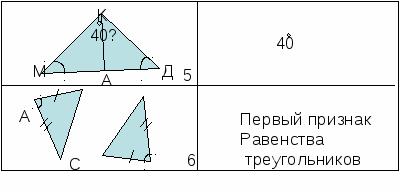


V. Историческая справка (заслушиваем доклад ученика 7 класса)
Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес (VI в. до н.э.). Ему принадлежит открытие следующих теорем:
-
Вертикальные углы равны.
-
В равнобедренном треугольнике углы, лежащие при основании, равны.
-
Угол, вписанный в полуокружность, прямой.
-
Теорема о равенстве двух треугольников по стороне и двум прилежащим к ней углам.
Последней теореме Фалес нашел важное практическое приложение:
в гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В, С (АВ = ВС) и размеченную прямую СК ┴СА. При появлении корабля на прямой СК находили точку D такую, чтобы точки D, В, Е оказывались на одной прямой. Как ясно из чертежа, расстояние на земле CD и является искомым расстоянием до корабля АЕ по воде.
Попытки греческих ученых привести геометрические факты в систему начинаются уже с V в. до н. э. Наибольшее влияние на все последующее развитие геометрии оказали труды греческого ученого Евклида, жившего в Александрии в III в. до н.э. Сочинение Евклида «Начала» почти два тысячелетия служило основной книгой, по которой изучали геометрию.
VI. Задание на дом: п.15; п.19; п.20 Стр.49- 50 вопрсы 1-15.
Рефлексия
![]()