- Учителю
- Диагностическая контрольная работа по геометрии 8 класс
Диагностическая контрольная работа по геометрии 8 класс
Діагностична контрольна робота з геометрії
у 8-х класах
Зміст завдань відповідає діючій програмі для загальноосвітніх навчальних закладів.
Пропонується 20 варіантів роботи.
Кожен варіант складається з трьох частин, які відрізняються за складністю та формою тестових завдань.
У І частині контрольної роботи запропоновано п'ять завдань з вибором однієї правильної відповіді, що відповідають початковому та середньому рівням навчальних досягнень учнів. До кожного завдання подано чотири варіанти відповіді, з яких тільки один правильний. Завдання вважається виконаним правильно, якщо учень указав тільки одну літеру, якою позначений правильний варіант відповіді.
Правильна відповідь за кожне із завдань 1-5 - оцінюється одним балом.
ІІ частина контрольної роботи складається з двох завдань, що відповідають достатньому рівню навчальних досягнень учнів. Розв'язання повинно мати короткий запис рішення без обґрунтування. Правильне розв'язання кожного із завдань цього блоку оцінюється двома балами.
ІІІ частина контрольної роботи складається з одного завдання, що відповідає високому рівню навчальних досягнень учнів, розв'язання якого повинно мати розгорнутий запис рішення з обґрунтуванням. Правильне розв'язання завдання цього блоку оцінюється трьома балами.
Контрольна робота розрахована на 45 хвилин.
Сума балів нараховується за правильно виконані учнем завдання відповідно максимально можливій кількості запропонованих балів для кожного блоку (5; 4; 3-всього 12балів). Контрольна робота розрахована на 45 хвилин.
Контрольні роботи виконуються у зошитах або на окремих аркушах.
При виконанні роботи необхідно указати номер завдання, текст завдань переписувати не обов'язково.
Примітка. У тексти завдань можна вносити корективи: збільшити (зменшити) кількість завдань або посилити (послабити) ступінь складності. Корективи обов'язково обґрунтувати.
Зразок підпису роботи
Діагностична контрольна робота
з алгебри
учня (учениці) ____8_____ класу
______________________________
назва навчального закладу
______________________________
прізвище ім'я в родовому відмінку
Варіант _____
Звіт з математики
ЗНЗ_________________________________________
Табл.1. Кількісний звітКіл-ть
учнів
Писало
Результати
І рівня
ІІ рівня
ІІІ рівня
ІV рівня
кільк.
%
кільк.
%
кільк.
%
кільк.
%
Табл.2. Якісний звіт
Всього
учнів
Писало
Правильна відповідь завдань у %
Кількість набраних балів у %
Кількість набраних балів у %
Кількість набраних балів у %
Кіл-ть
%
1
2
3
4
5
6 завдання
7 завдання
8 завдання
0
1
2
0
1
2
0
1
2
3
Аналітичний звіт.
Відзначити який матеріал засвоєно якісно.
Які допущені помилки. Причини виникнення та шляхи їх подолання.
Примітка. Якщо у тексти завдань були внесені корективи, необхідно надіслати текст з обов'язковим обґрунтуванням.
Директор підпис прізвище, ініціали
Печатка
Виконавець
Варіант 1
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Скільки точок треба взяти між точками А та В, щоб разом з відрізком АВ отримати шість різних відрізків?
А) 2; Б) 3; В) 4; Г) 5.
-
З
 найдіть
за даним рисунком пару суміжних кутів.
найдіть
за даним рисунком пару суміжних кутів.
А) ![]() АОВ та
АОВ та
![]() ВОС;
ВОС;
Б) ![]() АОВ та
АОВ та
![]() СОD;
СОD;
В) ![]() ВОС та
ВОС та
![]() СОD;
СОD;
Г) ![]() АОС та
АОС та
![]() СОD.
СОD.
-
У трикутнику MNK MN = NK, MN = 2 см, а периметр трикутника MNK дорівнює 5 см. Знайдіть сторону MK.
А) 1 см; Б) 2 см; В) 3 см; Г) 4 см.
-
Кут при основі рівнобедреного трикутника становить 130% кута при вершині. Знайдіть кути трикутника.
А) 50°, 65°, 65°; Б) 55°, 60°, 65°; В) 40°, 60°, 80°; Г) 90°; 30°;60°.
-
Обчисліть довжину кола, якщо його радіус дорівнює 5 см.
А) 20π см; Б) 2,5π см; В) 5π см; Г) 10π см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
 AOB=164°.
Промінь ОС поділяє його на два кути, градусні міри яких
відносяться як 3 : 1. Знайдіть ці кути.
AOB=164°.
Промінь ОС поділяє його на два кути, градусні міри яких
відносяться як 3 : 1. Знайдіть ці кути.
-
У колі з центром О проведено діаметри АВ і СD, АВ = 20 см, АС = 6 см. Знайдіть периметр ΔBOD.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
На сторонах кута М відкладено рівні відрізки МА і МВ. На бісектрисі кута М відкладено відрізки МК і МС, причому МС > MK. Доведіть рівність трикутників СКВ і СКА.
Варіант 2
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Скільки існує різних відрізків з кінцями в точках А, В, С, D, якщо три з цих точок лежать на одній прямій, а четверта не лежить на цій прямій?
А) 3; Б) 4; В) 5; Г) 6
-
Знайдіть за даним рисунком пару суміжних кутів.
А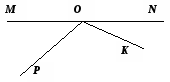 )
)
![]() MOP та
MOP та
![]() NOP;
NOP;
Б) ![]() POK та
POK та
![]() NOK;
NOK;
В) ![]() NOK та
NOK та
![]() PОN;
PОN;
Г) ![]() PОK та
PОK та
![]() MОP.
MОP.
-
У трикутнику EFP EF = EP, FP = 1,5EF. Периметр трикутникa EFP дорівнює 7 см. Знайдіть сторону FP.
А) 1 см; Б) 2 см; В) 3 см; Г) 1,5 см.
-
Кут при основі рівнобедреного трикутника в 2 рази більший від кута при вершині. Знайдіть кути трикутника.
А) 36°, 72°, 72°; Б) 50°, 65°, 65°; В) 80°, 50°, 50°; Г) 90°; 30°;60°.
-
Обчисліть діаметр кола, якщо довжина кола дорівнює 40π см.
А) 20 см; Б) 40 см; В) 80 см; Г) 60 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Промінь MF поділяє розгорнутий кут EMH у відношенні 1 : 2. Знайдіть ці кути.
-
У колі з центром О проведено діаметр АC і хорду AB,
 ВАС =
40°. Знайдіть
ВАС =
40°. Знайдіть  ВОС.
ВОС.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
На бісектрисі кута К відкладено відрізки КА і КМ, причому КМ > КА, а на сторонах кута К взято точки В і С так, що ВА = АС, ВМ = МС. Доведіть, що ∆ВКА = ∆СКА.
Варіант 3
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Скільки існує різних відрізків з кінцями в точках А, В, С, D, якщо жодні три з цих точок не лежать на одній прямій?
А) 6; Б) 5; В) 4; Г) 3.
-
Один із суміжних кутів дорівнює 58°. Чому дорівнює інший кут?
А) 122°; Б) 32°; В) 116°; Г) 29°.
-
KD - бісектриса рівнобедреного трикутника MNK з основою MN. Знайдіть MD, якщо MN = 40 см.
А) 20 см; Б) 60 см; В) 80 см; Г) 15 см.
-
Чому дорівнює кут між бісектрисами гострих кутів прямокутного трикутника?
А) 135°; Б) 120°; В) 150°; Г) 140°.
-
Обчисліть радіус кола, якщо довжина кола дорівнює 30π см.
А) 15 см; Б) 30 см; В) 60 см; Г) 40 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Знайдіть кут між бісектрисою та продовженням однієї із сторін даного кута, який дорівнює 50°.
-
MS − хорда, MK − дотична до кола в точці M, кут SMK дорівнює 34°.Знайти
 MOS,
де О − центр кола.
MOS,
де О − центр кола.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Відрізок DМ − бісектриса трикутника СDЕ. Через точку М проведена пряма, яка паралельна стороні DE і перетинає сторону DЕ у точці N. Знайдіть кути трикутника DMN, якщо кут CDE дорівнює 68°.
Варіант 4
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Промінь с проходить між сторонами кута (ав), який дорівнює 90°. Знайдіть кути (ас) та (вс), якщо кут (ас) вдвічі більший, ніж кут (вс).
А) 25° та 60°; Б) 60° та 30°; В) 35° та 55°; Г) 44° та 46°.
-
Знайдіть суміжні кути, якщо один з них у 2 рази більший, ніж другий.
А) 120° та 60°; Б) 90° та 45°; В) 60° та 30°; Г) 89° та 91°.
-
BD - висота рівнобедреного трикутника АВС з основою АС. Знайдіть DС, якщо АС = 12 см.
А) 3 см; Б) 6 см; В) 12 см; Г) 24 см.
-
Бісектриси кутів А і С трикутника АВС перетинаються в точці О під кутом 121°. Знайдіть кут В.
А) 62°; Б) 90°; В) 45°; Г) 59°.
-
Кола, радіуси яких 30 см і 40 см, мають зовнішній дотик. Знайдіть відстань між їх центрами.
А) 50 см; Б) 10 см; В) 70 см; Г) 60 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Знайдіть кут між бісектрисою та продовженням однієї із сторін даного кута, який дорівнює 90°.
-
У колі с центром О проведено діаметр ТМ і хорду МК, кут ОМК дорівнює 30°. Знайдіть кут TОК.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
Відрізок АD - бісектриса трикутника АВС. Через точку D проведена пряма, яка паралельна стороні АВ і перетинає сторону АС в точці F. Знайдіть кути трикутника АDF, якщо кут ВАС дорівнює 72°.
Варіант 5
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Якщо на малюнку ВD = 12 см, СD = 9 см, то ВС дорівнює:
А) 21 см; Б) 3 см; В) 6 см; Г) 2 см.

-
a
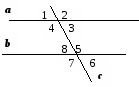 || b,
|| b,  = 54°, с − січна. Знайдіть
= 54°, с − січна. Знайдіть  4 та
4 та
 2.
2.
А) 54° та 54°;
Б) 54° та 36°;
В) 126° та 126°;
Г) 54° та 126°.
-
У рівнобедреному трикутнику АВС АВ = 7 см, ВС = 5 см. Знайдіть периметр ∆ABC, якщо його основою є сторона AB.
А) 12 см; Б) 17 см; В) 19 см; Г) 20 см.
-
Трикутники BCD і AFE рівні. Знайдіть сторону AE, якщо ВС = 7 см, EF = 14 см, P∆BCD = 29 см.
А) 29 см; Б) 13 см; В) 8 см; Г) 4 см.
-
Кола, радіуси яких 3 см і 2 см, мають внутрішній дотик. Знайдіть відстань між їх центрами.
А) 10 см; Б) 8 см; В) 5 см; Г) 1 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Знайдіть кут між бісектрисою та продовженням однієї із сторін даного кута, який дорівнює 72°.
-
З однієї точки М проведено дві дотичні до кола. Знайдіть відрізок дотичної МР, якщо відрізок дотичної MQ дорівнює 15 см, Р і Q - точки дотику.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
По один бік від прямої АВ позначено точки Q і D так, що
 QAD =
QAD =
 DBQ і
DBQ і
 DAB =
DAB =
 QBA.
Доведіть, що AQ = BD і AD = BQ.
QBA.
Доведіть, що AQ = BD і AD = BQ.
Варіант 6
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Знайдіть кут між бісектрисою та стороною кута, який дорівнює 50°.
А) 130°; Б) 75°; В) 25°; Г) 100°.
-
a || b, с − січна,
 3
= 20°. Знайдіть
3
= 20°. Знайдіть  5 −
5 −
 6.
6.
А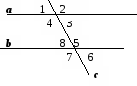 )
20°;
)
20°;
Б) 140°;
В) 0°;
Г) 160°.
-
У рівнобедреному трикутнику MNF MF = 10 см, MN = 8 см. Знайдіть периметр ∆MNF, якщо бічними сторонами є сторони MN і NF.
А) 18 см; Б) 26 см; В) 28 см; Г) 30 см.
-
У рівнобедреному трикутнику АВС відрізок ВD - медіана, АС - основа. Знайдіть РDАВС, якщо РDАВD = 12 см, ВD = 4 см.
А) 24 см; Б) 16 см; В) 20 см; Г) інша відповідь.
-
Знайдіть довжину кола, якщо площа круга 36π.
А) 12π; Б) 6π; В) 3π; Г) 24π.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
 AOB =
124°. Промінь ОС поділяє його на два кути, різниця яких
дорівнює 34°. Знайдіть ці кути.
AOB =
124°. Промінь ОС поділяє його на два кути, різниця яких
дорівнює 34°. Знайдіть ці кути.
-
У трикутнику АВС проведена медіана АМ. Знайдіть периметр трикутника АВС, якщо ВМ = 4 см, АВ = 5 см, а АС удвічі більша за АВ.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
В трикутнику SМР кут Р дорівнює 59°. На стороні SР взято точку К так, що відрізок КМ дорівнює відрізку КР. Знайдіть кут КМР.
Варіант 7
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Знайдіть кут, якщо його бісектриса утворює з його стороною кут, який дорівнює 60°.
А) 30°; Б) 180°; В) 90°; Г) 120°.
-
Один із суміжних кутів у 3 рази менший від іншого. Знайдіть ці кути.
А) 60° та 120°; Б) 60° та 20°; В) 45° та 135°; Г) 45° та 15°.
-
У рівнобедреному трикутнику XYZ YZ = 6 см, XZ = 8 см. Знайдіть периметр ∆XYZ, якщо його бічними сторонами є сторони XY і XZ.
А) 14 см; Б) 20 см; В) 22 см; Г) 30 см.
-
∆
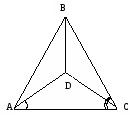 АВС і
∆ADC - рівнобедрені з основою АС. Знайдіть ÐBAD, якщо ÐDАС =
48º, ÐВСА = 67º.
АВС і
∆ADC - рівнобедрені з основою АС. Знайдіть ÐBAD, якщо ÐDАС =
48º, ÐВСА = 67º.
А) 38º; Б) 115º; В) 19º; Г) 67º
67º
48º
-
Знайдіть площу круга, якщо довжина кола 6π.
А) 36π; Б) 9π; В) 3π; Г) 12π.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Між сторонами кута (аb), який дорівнює 60°, проходить промінь с. Знайдіть
 (ac)
та
(ac)
та  (bc),
якщо
(bc),
якщо  (ac)
на 30° більше, ніж
(ac)
на 30° більше, ніж  (bc).
(bc).
-
У трикутнику АВС проведена медіана ВЕ. Знайдіть довжину АЕ, якщо АВ = 6 см, периметр трикутника АВС дорівнює 18 см, а ВС на 2 см більша за АВ.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У рівнобедрений трикутник вписано коло, що ділить бічну сторону у відношенні 3 : 2, починаючи від основи. Знайдіть бічну сторону трикутника, якщо його периметр дорівнює 48 см.
Варіант 8
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Від прямої АВ в даній півплощині відкладені
 ВАС =
30° та
ВАС =
30° та  BAD =
70°. Знайдіть
BAD =
70°. Знайдіть  СAD.
СAD.
А) 100°; Б) 40°; В) 50°; Г) 35°.
-
Знайдіть вертикальні кути, якщо їх сума дорівнює 130°.
А) 130°; 130°; Б) 130°; 50°; В) 65°; 65°; Г) 60°; 60°.
-
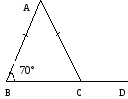
У трикутнику АВС АВ = АС, ÐАВС = 70º. Знайдіть кут АСD.
А) 70°; Б) 90°; В) 110°; Г) 40º.
-
Периметр рівнобедреного трикутника 41 см, бічна сторона на 3,5 см менша за основу. Знайдіть основу трикутника.
А) 17,5 см; Б) 16 см; В) 15 см; Г) 12,5 см.
-
Діаметр кола на 4 см більший за радіус даного кола. На якій відстані від центра знаходиться дотична до кола?
А) 12 см; Б) 16 см; В) 8 см; Г) 4 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
 AOB=164°.
Промінь ОС поділяє його на два кути, градусні міри яких
відносяться як 3 : 1. Знайдіть ці кути.
AOB=164°.
Промінь ОС поділяє його на два кути, градусні міри яких
відносяться як 3 : 1. Знайдіть ці кути.
-
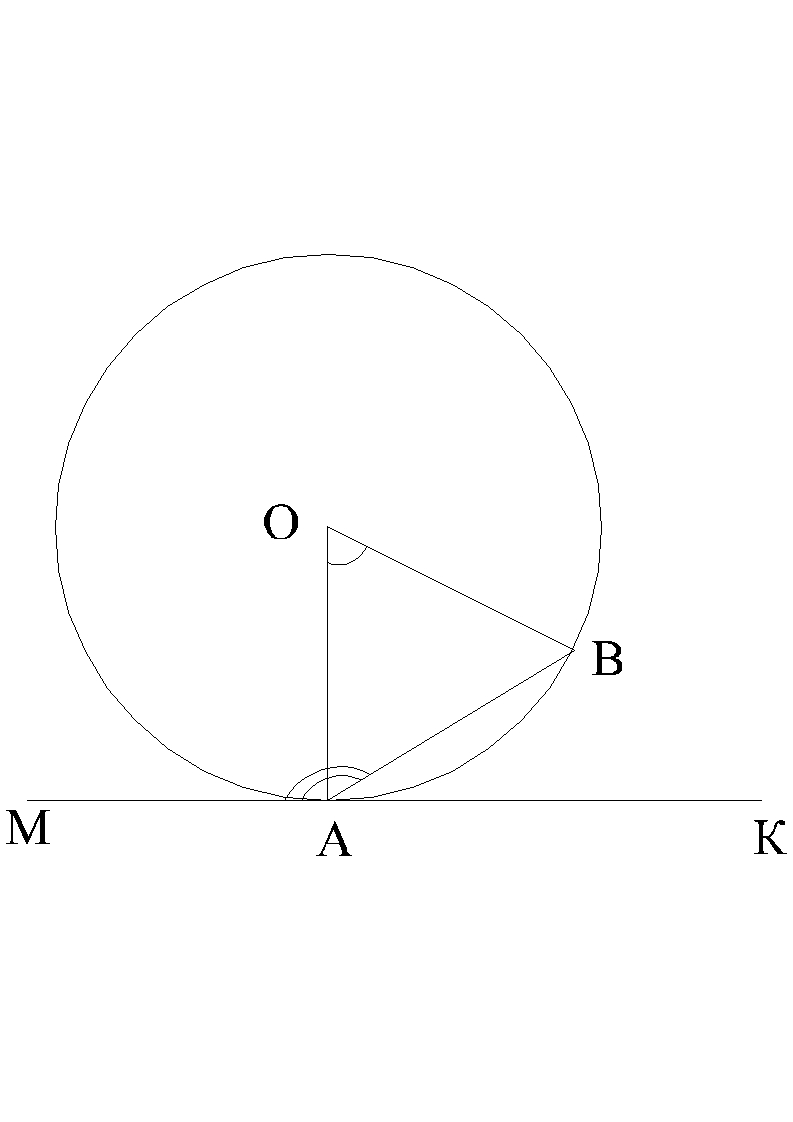
П
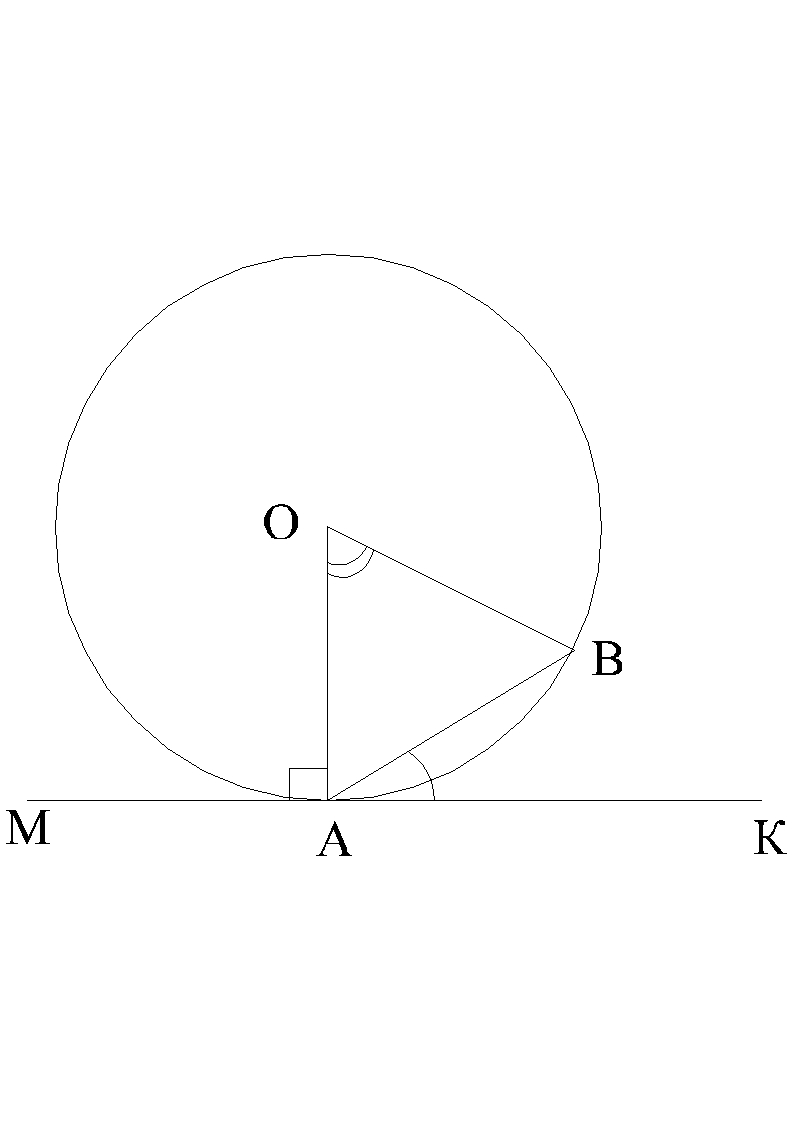 ряма
МК дотикається до кола з центром О в точці А, відрізок АВ -
хорда кола,
ряма
МК дотикається до кола з центром О в точці А, відрізок АВ -
хорда кола,  ВАК =
25°. Знайдіть
ВАК =
25°. Знайдіть  АОВ.
АОВ.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У рівнобедреному трикутнику АВС з основою АС проведено висоту ВК, яка дорівнює 12 см. Периметр трикутника АВК дорівнює 40 см. Чому дорівнює периметр ∆АВС?
Варіант 9
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
 (ав)
= 40°;
(ав)
= 40°;  (ас)=90°,
промені в та с знаходяться в одній півплощині. Знайдіть
(ас)=90°,
промені в та с знаходяться в одній півплощині. Знайдіть
 (вс).
(вс).
А) 130°; Б) 65°; В) 50°; Г) 45°.
-
Сума двох вертикальних кутів дорівнює 210°. Знайдіть ці кути.
А) 105°; 105°; Б) 30°; 180°; В) 210°; 90°; Г) 105°; 75°.
-
У трикутнику XYZ YX = YZ, ÐYXZ = 70º. Знайдіть величину кута FZD.
А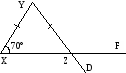 )
70º; Б) 90º; В) 110º; Г) 125º.
)
70º; Б) 90º; В) 110º; Г) 125º.
-
Периметр рівнобедреного трикутника CDE дорівнює 26 см, СЕ - основа, DB - бісектриса. P∆DBE = 20 см. Знайдіть DB.
А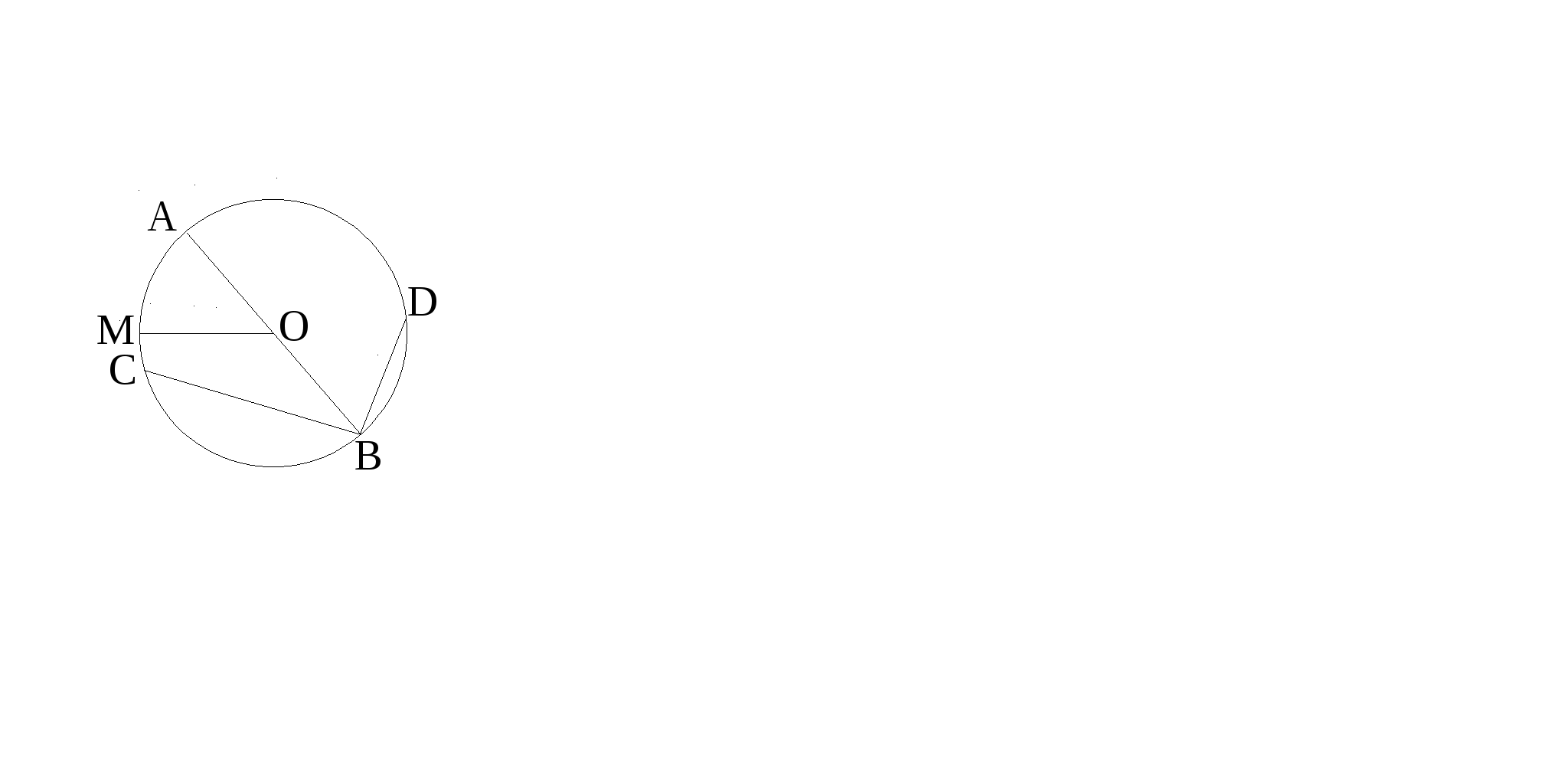 ) 9
см; Б) 8 см; В) 7 см; Г) 6 см.
) 9
см; Б) 8 см; В) 7 см; Г) 6 см.
-
Скільки хорд зображено на рисунку?
А) 0; Б) 1;
В) 2; Г) 3.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Промінь MF поділяє розгорнутий кут EMH у відношенні 1 : 2. Знайдіть ці кути.
-
П
 ряма
МК дотикається до кола з центром О в точці А, відрізок АВ -
хорда кола,
ряма
МК дотикається до кола з центром О в точці А, відрізок АВ -
хорда кола,  АОВ =
70°. Знайдіть
АОВ =
70°. Знайдіть  ВАМ.
ВАМ.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У рівнобедреному ∆DВС з основою DС проведено бісектрису ВК, яка дорівнює 8 см. Периметр трикутника DВК дорівнює 24 см. Чому дорівнює периметр ∆DВС?
Варіант 10
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
 (сb)
на 30° більший, ніж
(сb)
на 30° більший, ніж  (ас).
Знайдіть
(ас).
Знайдіть  (ас).
(ас).
А )
75°; Б) 105°; В) 150°; Г) 30°.
)
75°; Б) 105°; В) 150°; Г) 30°.
-
Сума вертикальних кутів, утворених при перетині двох прямих, дорівнює 140°. Знайдіть градусні міри всіх чотирьох кутів.
А) 70°, 70°, 110°, 110°; Б) 140°, 140°, 40°, 40°;
В) 70°, 70°, 20°, 20°; Г) 20°, 20°, 160°, 160°.
-
Знайдіть третю сторону рівнобедреного трикутника, якщо дві його сторони дорівнюють 8 см і 3 см.
А) 5 см; Б) 3 см; В) 8 см; Г) 8 см або 3 см.
-
У трикутнику АВС ÐА = ÐС, висота AD поділяє сторону ВС навпіл. Знайдіть АС, якщо BD = 7,8 см.
А) 10,7 см; Б) 11,7 см; В) 7,8 см; Г) 15,6 см.
-
АВ і CD - діаметри кола. Знайдіть довжину хорди АС, якщо довжина хорди ВD дорівнює 8 см.
А) 8 см; Б) 10 см; В) 14 см; Г) 16 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Прямий кут поділений на три частини, градусні міри яких відносяться як 2 : 3 : 4. Знайдіть величини цих частин.
-
С
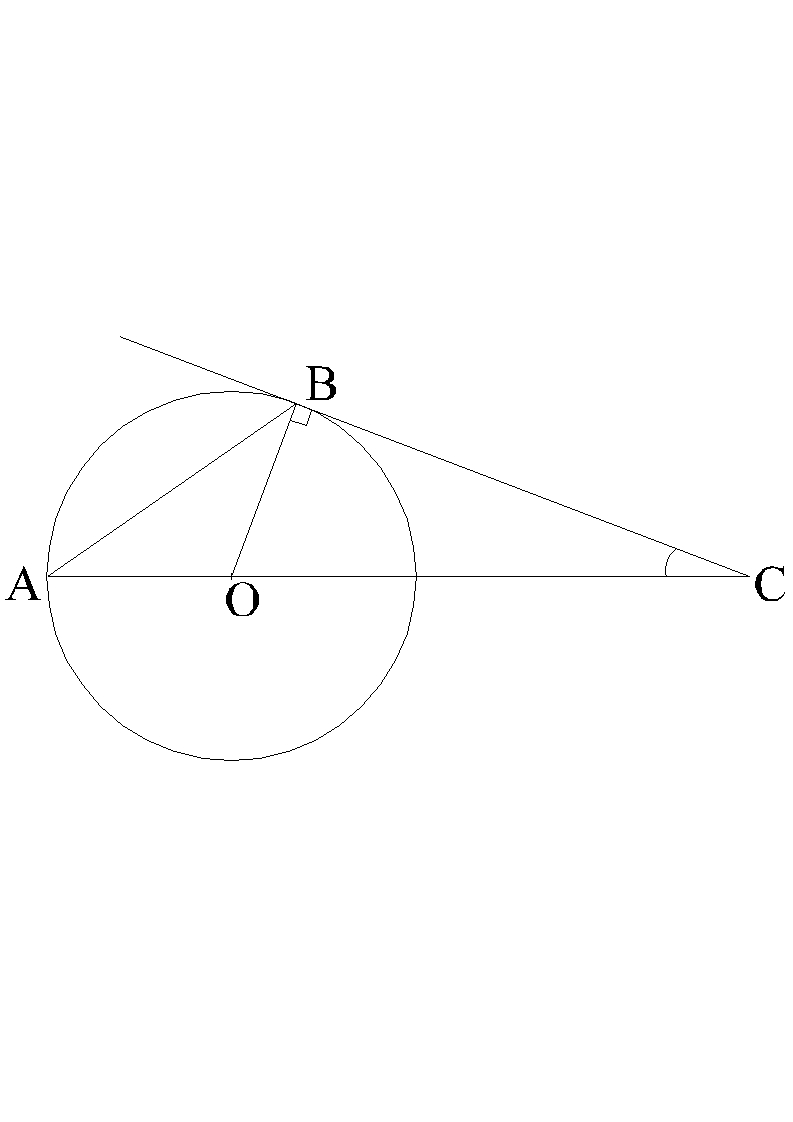 В -
дотична,
В -
дотична,  С
= 20°. Знайдіть кути ΔАОВ.
С
= 20°. Знайдіть кути ΔАОВ.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У рівнобедреному трикутнику АВО з основою АО проведено висоту ВК, яка дорівнює 16 см. Периметр трикутника АВК дорівнює 40 см. Чому дорівнює периметр трикутника АВО?
Варіант 11
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-

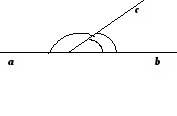 (сb)
на 40°менший, ніж
(сb)
на 40°менший, ніж  (ас).
Знайдіть
(ас).
Знайдіть  (сb).
(сb).
А) 140°; Б) 40°;
В) 110°; Г) 70°.
-
Сума двох вертикальних кутів, що утворилися при перетині двох прямих, дорівнює 130°. Знайдіть градусні міри всіх чотирьох кутів.
А) 130°, 130°, 50°, 50°; Б) 90°, 90°, 40°, 40°;
В) 115°, 115°, 65°, 65°; Г) 30°, 30°, 100°, 100°.
-
Знайдіть третю сторону рівнобедреного трикутника, якщо дві його сторони дорівнюють 10 см і 5 см.
А) 4 см; Б) 5 см; В) 10 см; Г) 10 см або 5 см.
-
У трикутнику MPE проведена медіана PK, відомо, що PK = MP і ÐМ = 54º. Знайдіть кут РKЕ.
А) 153º; Б) 54º; В) 126º; Г) 134º.
-
З точки М до кола проведені дотичні МА і МВ (А і В - точки дотику). Яке твердження є правильним?
А) МА ≠ МВ; Б) МА = МВ; В) МА > МВ; Г) МА < МС.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Розгорнутий кут поділений на три частини, градусні міри яких відносяться як 3 : 4 : 2. Знайдіть величини цих частин.
-
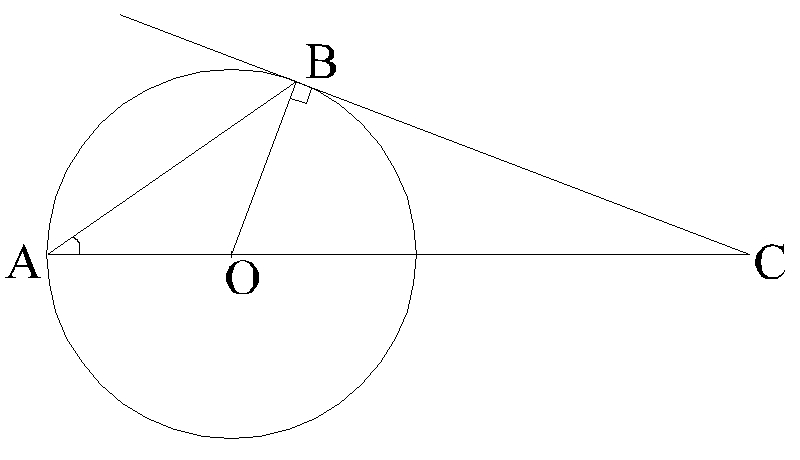
СВ - дотична,
 А =
30°. Знайдіть кути ΔВОС.
А =
30°. Знайдіть кути ΔВОС.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У рівнобедреному трикутнику АВС з основою АС проведено бісектрису ВD, що дорівнює 10 см. Периметр трикутника АВD дорівнює 34 см. Чому дорівнює периметр ∆АВС?
Варіант 12
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Яка з трьох точок лежить між двома іншими, якщо АВ = 5 см, АС = 7 см, ВС = 2 см.
А) В; Б) А; В) С; Г) жодна.
-
Сума двох кутів, утворених при перетині двох прямих, дорівнює 60°. Знайдіть ці кути.
А) 120° та 60°; Б) 10° та 50°; В) 30° та 30°; Г) 40° та 20°.
-
У трикутнику MKP MK = KP, KF
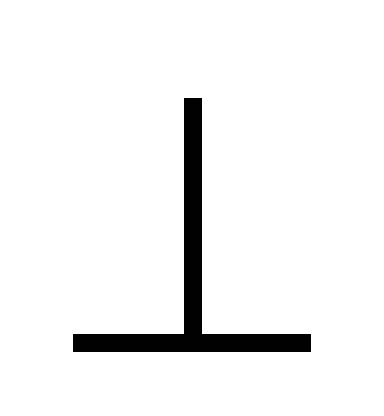 MP,
ÐFKP = 35º. Знайдіть ÐMKP.
MP,
ÐFKP = 35º. Знайдіть ÐMKP.
А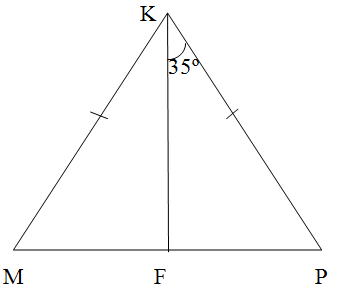 )
35º; Б) 70º; В) 90º; Г) 55º.
)
35º; Б) 70º; В) 90º; Г) 55º.
-
Периметр рівнобедреного трикутника 27 см, основа на 4,5 см більша, ніж бічна сторона. Знайдіть бічну сторону трикутника.
А) 10,5 см; Б) 9 см; В) 8,5 см; Г) 7,5 см.
-
Вкажіть, яку з наведених далі побудов можна виконати за допомогою одного тільки циркуля:
А) провести довільну пряму;
Б) побудувати промінь, який виходить з даної точки та проходить через другу дану точку;
В) відкласти на даній прямій від даної на ній точці відрізок, який дорівнює даному;
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Один із кутів, які утворюються при перетині двох прямих, у 4 рази більше другого. Знайдіть кути.
-
К
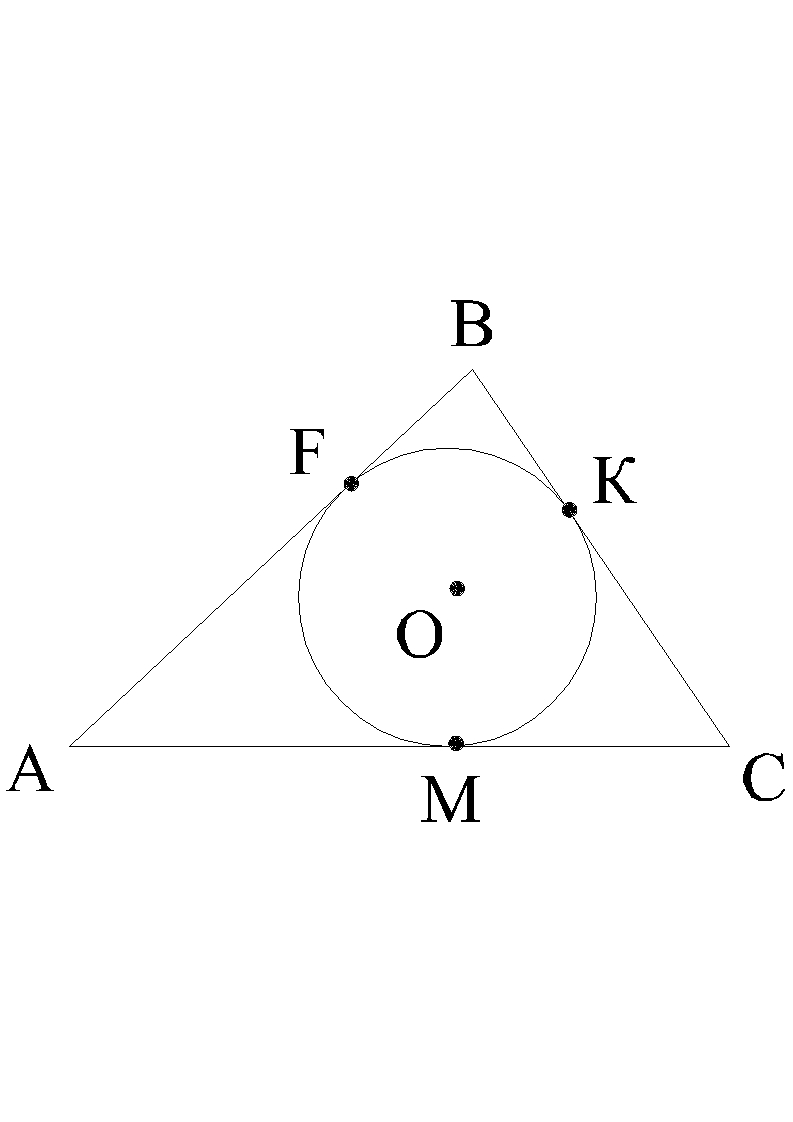 оло,
вписане в ΔАВС, дотикається до його сторін у точках F, K, M. AF
= 9 см, BK = 1 см, CM = 5 см. Знайдіть периметр ΔАВС.
оло,
вписане в ΔАВС, дотикається до його сторін у точках F, K, M. AF
= 9 см, BK = 1 см, CM = 5 см. Знайдіть периметр ΔАВС.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
Периметр рівнобедреного трикутника в 4 рази більший за основу і на 10 см більший за бічну сторону. Знайдіть сторони трикутника.
Варіант 13
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Яка з трьох точок лежить між двома іншими, якщо МА = 3 см, АN = 4 см, МN = 7 см.
А) М; Б) А; В) жодна; Г) N.
-
Сума трьох кутів, утворених при перетині двох прямих, дорівнює 265°. Знайдіть більший з кутів.
А) 95°; Б) 180°; В) 85°; Г) 165°.
-
З
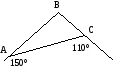 а
даними рисунка знайдіть
а
даними рисунка знайдіть  В:
В:
А) 80°; Б) 100°;
В) 110°; Г) 40°.
-
Периметр рівнобедреного трикутника АВС дорівнює 28 см. АС - основа, BD - висота, P∆DBC = 18 см. Знайдіть BD.
А) 5 см; Б) 8 см; В) 4 см; Г) 10 см.
5. Знайдіть ширину кільця, одержаного концентричними колами з радіусами 3 см і 9 см.
А) 12 см; Б) 6 см; В) 5 см; Г) 3 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Один із кутів, які утворюються при перетині двох прямих, у 3 рази менше другого. Знайдіть кути.
-
У трикутнику одна з його сторін дорівнює 28 см, а інша сторона ділиться точкою дотику, вписаного в нього кола, на відрізки 12 см і 14 см. Знайдіть периметр трикутника.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
Бічна сторона рівнобедреного трикутника в 2 рази більша за основу і на 12 см менша за периметр трикутника. Знайдіть сторони трикутника.
Варіант 14
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Яка з трьох точок А, В, С прямої лежить між двома іншими, якщо АВ = 5 см, ВС = 3 см, АС = 8 см.
А) В; Б) С; В) А; Г) інша відповідь.
-
Якщо один із суміжних кутів удвічі більший за другий, то градусна міра меншого з цих кутів дорівнює:
А) 30°; Б) 60°; В) 45°; Г) 120°.
-
Знайдіть кут між бічними сторонами рівнобедреного трикутника, якщо один із кутів при основі дорівнює 35º.
А) 110º; Б) 35º; В) 60º; Г) 90º.
-
У

 рівних трикутниках АВС і А
рівних трикутниках АВС і А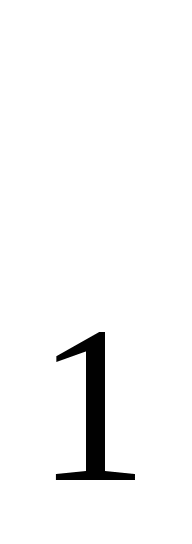 В
В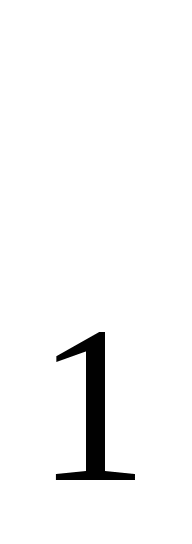 С
С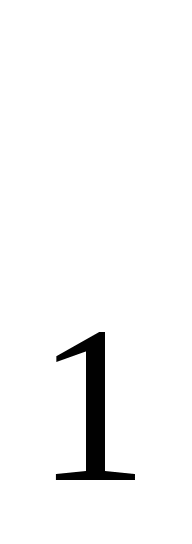 АВ =
3 см, ВС = 4 см. Периметр
АВ =
3 см, ВС = 4 см. Периметр  АВС
дорівнює 12 см. Знайдіть сторону А
АВС
дорівнює 12 см. Знайдіть сторону А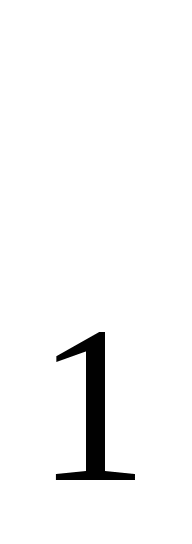 С
С .
.
А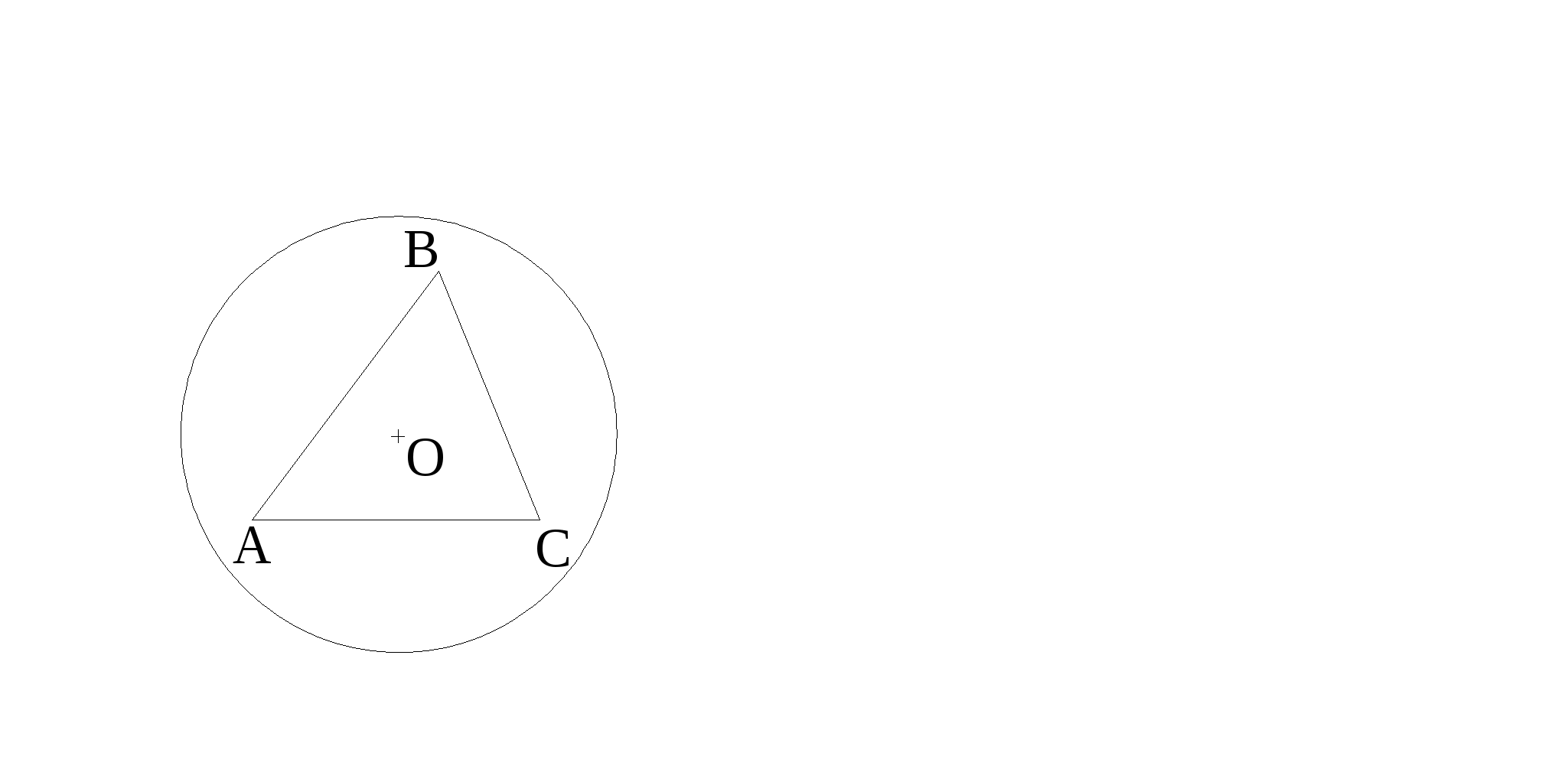 ) 3
см; Б) 5 см; В) 4 см; Г) 7 см.
) 3
см; Б) 5 см; В) 4 см; Г) 7 см.
-
Н
 а
якому з рисунків зображене коло, вписане в трикутник?
а
якому з рисунків зображене коло, вписане в трикутник?
А) Б) В) Г)
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Сума двох кутів, які утворюються при перетині двох прямих, дорівнює 1200. Знайдіть ці кути.
-
В гострокутному трикутнику МNР бісектриса кута М переринає висоту NК у точці О, де ОК = 9 см. Знайдіть відстань від точки О до прямої МN.
III частина (3 бали)
Розв'язання завдання 8повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Три кола попарно мають зовнішній дотик. Відрізки, які з'єднують їх центри, утворюють трикутник із сторонами 9 см, 10 см і 11 см. Знайдіть радіуси кіл.
Варіант 15
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Яка з трьох точок А, В, С прямої лежить між двома іншими, якщо АВ = 8 см, ВС = 5 см, АС = 3 см.
А) В; Б) С; В) А; Г) інша відповідь.
-
Один з кутів, утворених при перетині двох прямих, на 50° менший від другого. Знайдіть ці кути.
А) 95° та 45°; Б) 130° та 80°; В) 65° та 115°; Г) 115° та 165°.
-
У рівних трикутниках МКР і ЕDС ЕD = 6 см, DС = 5 см. Периметр ∆ЕСD дорівнює 14 см. Знайдіть сторону МP.
А) 5 см; Б) 6 см; В) 3 см; Г) 11 см.
-
Знайдіть кут при основі рівнобедреного трикутника, якщо кут між бічними сторонами дорівнює 20º.
А) 30º; Б) 60º; В) 80º; Г) 160º.
-
У трикутнику АВС відрізок BD є висотою. Яка з наведених рівностей випливає з цієї умови?
А) АВ = ВС; Б) кут BAD - прямій;
В) AD = DC; Г) кут DAB − прямій.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Різниця двох із кутів, які утворюються при перетині двох прямих, дорівнює 140°. Знайдіть ці кути.
-
У прямокутному трикутнику DСЕ с прямим кутом С проведена бісектриса ЕF, де FС = 13 см.Знайдіть відстань от точки А до прямої DЕ.
III частина (3 бали)
Розв'язання завдання 8повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
8. Три кола попарно мають зовнішній дотик. Відрізки, які з'єднують їх центри, утворюють трикутник із сторонами 7 см, 8 см і 9 см. Знайдіть радіуси кіл.
Варіант 16
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Якщо на малюнку АС = 12 см, ВС = 5 см, то АВ дорівнює:

А) 7 см; Б) 17 см; В) 6 см; Г) 8 см.
-
a || b,
 = 72°, с − січна. Знайдіть
= 72°, с − січна. Знайдіть  5 та
5 та
 7.
7.
А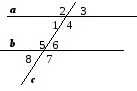 ) 72°
та 72°;
) 72°
та 72°;
Б) 108° та 108°;
В) 72° та 108°;
Г) 72° та 28°.
-
Знайдіть кут між бічними сторонами рівнобедреного трикутника, якщо один із кутів при основі дорівнює 36º.
А) 18º; Б) 36º; В) 72º; Г) 108º.
-
∆АВС = ∆А1В1С1, Р∆АВС = 39 см. Сторона А1В1 у 1,5 рази менша за сторону В1С1, а А1С1 на 3 см менша за сторону А1В1. Знайдіть більшу сторону трикутника АВС.
А) 15 см; Б) 16 см; В) 18 см; Г) 19 см.
-
АВ і CD - діаметри кола. Знайдіть довжину хорди ВС, якщо довжина хорди АD дорівнює 5 см.
А) 4 см; Б) 5 см; В) 6 см; Г) 7 см.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
У прямокутному трикутнику АВС з прямим кутом С, проведено бісектриси СD і АЕ які перетинаються у точці О. Кут АОС дорівнює 105º. Визначте гострі кути трикутника АВС.
-
Знайдіть сторони рівнобедреного трикутника,якщо його периметр дорівнює 20 см,причому бічна сторона на 2 см менша основи.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
Точка дотику вписаного кола ділить бічну сторону рівнобедреного трикутника на відрізки 4 см і 5 см, починаючи від основи. Знайдіть периметр трикутника.
Варіант 17
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Між сторонами кута (аb), який дорівнює 80°, проходить промінь с. Знайдіть кут (ас), якщо кут (сb) втричі менший від кута (ас).
А) 60°; Б) 20°; В) 40°; Г) 23°.
-
Знайдіть суміжні кути, якщо один з них на 20° менше, ніж другий.
А) 80° та 60°; Б) 35° та 145°; В) 85° та 65°; Г) 80° та 100°.
-
Якщо зовнішній кут DBC трикутника АВС дорівнює 100º та АВ = ВС, то кут А дорівнює:
А) 100º; Б) 80º; В) 50º; Г) 40º.
-
У рівносторонньому трикутнику проведено дві медіани. Чому дорівнює гострий кут між ними?
А) 60°; Б) 90°; В) 45°; Г) 30°.
-
Кут при основі рівнобедреного трикутника в 2 рази більший від кута при вершині. Знайдіть кути трикутника.
А) 36°, 72°, 72°; Б) 50°, 65°, 65°; В) 80°, 50°, 50°; Г) 90°; 30°;60°.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
В трикутнику DEF кут D дорівнює 50°, кут E дорівнює 70,°,О - точка перетину бісектрис кутів E і F. Знайдіть кут ЕОF.
-
Знайдіть сторони рівнобедреного трикутника,якщо його периметр дорівнює 20 см,причому бічна сторона на 1 см більша основи.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
Знайдіть довжину сторін трикутника, якщо точки дотику кола, вписаного в цей трикутник, поділяють його сторони на відрізки, два з яких дорівнюють 4 см і 2 см, а периметр дорівнює 18 см.
Варіант 18
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Відомо, що С - середина відрізка АВ. АВ = 15 дм. Знайдіть АС та СВ.
А) 7,5 м та 7,5 дм; Б) 7,5 дм та 75 см;
В) 7,5 см та 7,5 см; Г) 7,5 дм та 7,5 см.
-
а || b, с − січна,
 = 40°. Знайдіть
= 40°. Знайдіть  4 −
4 −
 2.
2.
А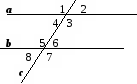 )
80°;
)
80°;
Б) 40°;
В) 100°;
Г) 0°.
-
Якщо зовнішній кут MNK трикутника PNM дорівнює 80º і PN = NM, то кут Р дорівнює:
А) 40º; Б) 50º; В) 60º; Г) 80º.
-
У рівносторонньому трикутнику проведено дві медіани. Чому дорівнює гострий кут між ними?
А) 60°; Б) 90°; В) 45°; Г) 30°.
-
Знайдіть другий гострий кут прямокутного трикутника,якщо один його гострий кут дорівнює:
А) 18°, Б) 36°; В) 54°; Г) 72°.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
Відрізок ВК - висота рівнобедреного трикутника АВС з основою АС. Кут ВАК дорівнює 48°.Знайдіть градусну міру кутів трикутника СВК.
-
В рівнобедреному трикутнику SLR з основою SR проведена медіана LK. Знайдіть її довжину, якщо периметр трикутника SLR дорівнює 48 см, а трикутника SLK дорівнює 32 см.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У трикутнику одна з сторін дорівнює 56 см, а інша сторона ділиться точкою дотику вписаного в трикутник кола, на відрізки 24 см і 28 см. Знайдіть периметр трикутника.
Варіант № 19
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Відомо, що точка С лежить між точками А та В. АС = 3 дм, СВ = 1,5 см. Знайдіть АВ.
А) 4,5 дм; Б) 4,5 см; В) 31,5 см; Г) 31,5 дм.
-
Один із суміжних кутів у 5 разів більший від іншого. Знайдіть ці кути.
А) 30° та 30°; Б) 15° та 75°; В) 36° та 144°; Г) 30° та 150°.
-
Величина кутів трикутника відноситься як 3 : 5 : 1. Знайдіть кути трикутника.
А) 100°, 60°, 20°; Б) 60°, 70°, 50°; В) 10°, 50°, 120°; Г) 90°; 30°; 60°.
-
Периметр рівнобедреного трикутника з основою 7 см і бічною стороною 6 см дорівнює:
А) 18 см; Б) 19 см; В) 20 см; Г) 13 см.
-
У рівних трикутниках ABC і KLM AC = 15 см, LM = 20 см, а периметр трикутника ABC дорівнює 60 см. Знайдіть сторону KL.
А) 15 см; Б) 20 см; В) 25 см; Г) 35 см.
II частина ( 4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
У
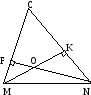 трикутнику CMN висоти MK і NF
перетинаються в точці О. Відомо, що CMN = 74º, CNM = 58º.
Знайдіть MON.
трикутнику CMN висоти MK і NF
перетинаються в точці О. Відомо, що CMN = 74º, CNM = 58º.
Знайдіть MON.
-
У колі с центром О проведено діаметр АВ і хорду АК, кут ОАК дорівнює 60°, АК = 5 см. Знайдіть довжину діаметра АВ.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У трикутнику, периметр якого дорівнює 200 см, одна з сторін ділиться точкою дотику вписаного в нього кола, на відрізки 30 см і 42 см. Знайдіть дві інші сторони трикутника.
Варіант 20
I частина (5 балів)
Завдання 1 - 5 мають по чотири варіанти відповіді, з яких тільки одна вірна. Виберіть вірну відповідь. Вірна відповідь кожного завдання оцінюється одним балом.
-
Точка В поділяє відрізок АС на два відрізки. Знайдіть довжину відрізка АС, якщо АВ = 7,8 см, ВС = 2,5 см.
А) 5,3 см; Б) 15,6 см; В) 5см; Г) 10,3 см.
-
а
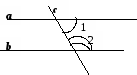 ||
b, с − січна,
||
b, с − січна,  2 −
2 −
 1 =
30°. Знайдіть
1 =
30°. Знайдіть  1 та
1 та
 2.
2.
А) 75° та 45°;
Б) 75° та 105°;
В) 105° та 135°;
Г) 150° та 120°.
-
Величини кутів трикутника відносяться як 4 : 3 : 2. Знайдіть кути трикутника.
А) 80°, 60°, 40°; Б) 100°, 60°, 20°; В) 10°, 70°, 100°; Г) 90°; 30°; 60°.
-
Периметр рівнобедреного трикутника 37 см, а його основа - 7 см. Знайдіть бічну сторону.
А) 30 см; Б) 23 см; В) 15 см; Г) 22 см.
-
У трикутнику ABC AC = BC. Знайдіть кут В, якщо кут BCD дорівнює 130°.
А) 65°; Б) 90°; В) 100°; Г) 130°.
II частина (4 бали)
Розв'язання завдань 6 - 7 повинно мати короткий запис рішення без обґрунтування. Вірне рішення кожного завдання оцінюється двома балами.
-
У
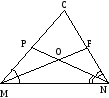 трикутнику MCN бісектриси MF і NP
перетинаються в точці О. Відомо, що FON = 65º. Знайдіть FMN +
PNM; MCN.
трикутнику MCN бісектриси MF і NP
перетинаються в точці О. Відомо, що FON = 65º. Знайдіть FMN +
PNM; MCN.
-
У прямокутному трикутнику катет завдовжки 12 см, прилеглий до кута 30º. Визначте висоту, проведену до гіпотенузи.
III частина (3 бали)
Розв'язання завдання 8 повинно мати розгорнутий запис рішення з обґрунтуванням кожного етапу. Завдання оцінюється трьома балами.
-
У рівнобедрений трикутник вписано коло, що ділить бічну сторону у відношенні 2 : 3, починаючи від основи. Знайдіть бічну сторону трикутника, якщо його периметр дорівнює 42 см.