Интегрированный урок в 9 классе по математике и биологии по теме «Возможности организмов и геометрическая прогрессия».

Интегрированный урок

математики и биологии в 9 классе.

Тема:

«Возможности организмов и геометрическая прогрессия».

Дидактическая цель:

Создать условия для осознания и осмысления вывода формулы n-го члена геометрической прогрессии.

Цели по содержанию урока:

1. Образовательная - способствовать осознанию того, что тема, изученная на уроке математики применяется на уроках биологии.

2. Развивающая - способствовать обучению школьников умению выделять математическую модель из практико-ориентированной задачи.

3. Воспитательная - способствовать эстетическому и экологическому воспитанию учащихся.

Тип урока - изучение нового материала.

Форма организации познавательной деятельности - фронтальная, групповая, индивидуальная.

Методы - проблемного изложения материала, частично-поисковый.

Оборудование: компьютер и мультимедийный проектор, наглядный материал (таблицы), тетрадь.

Приветствует учащихся;

Планирует возможность работы по 4 человека

Проверяют готовность к уроку.

2

Целеполагание и мотивация.

а) мотивация

ведёт беседу по следующим вопросам:

1. Любите ли вы смотреть фильмы, видеосюжеты?

2. Сейчас вы просмотрите видеофрагмент.

3. Посмотрев видеофрагмент, определите, о каком свойстве организмов идёт речь?

б) постановка темы урока.

в) постановка цели урока

формулирует вопросы:

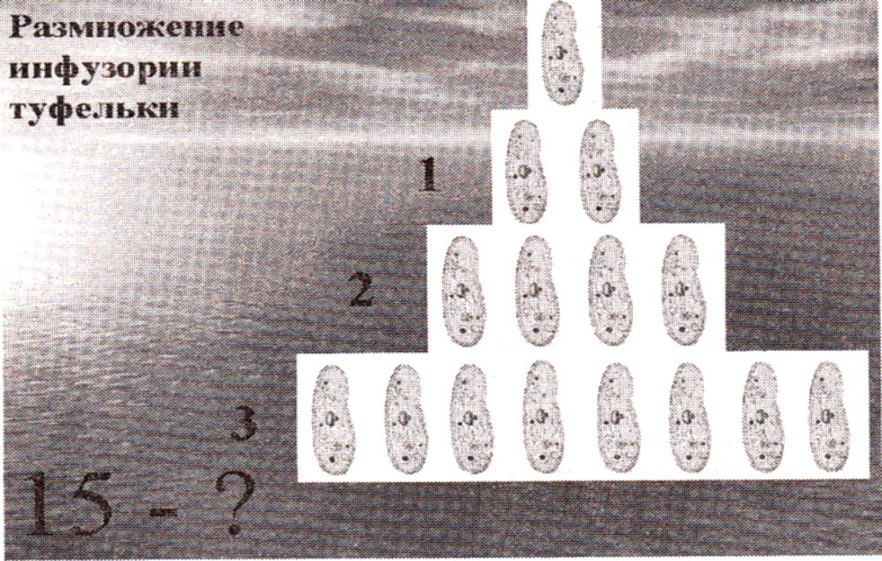
1. В какое время года и каким способом размножается инфузория-туфелька?

2. Сколько будет инфузорий после второго размножения?

3. Сколько после третьего размножения?

4. Сколько после 15 размножения?

5. Рассмотрим последовательность размножений:

1; 2; 4; 8; 16;32; 64; …

Какое предположение можно сделать, анализируя данную последовательность?

6. Как вы определили, что это геометрическая прогрессия?

7. Что нам нужно знать для ответа на вопрос: «Сколько инфузорий будет после 15 размножения? » (табл.1)

8. Можно ли упростить процесс вычисления? (табл.1)

Отвечают на вопросы учителя.

Формулируют тему урока.

Летом инфузории размножаются бесполым способом деления пополам.

4.

8.

???

Это геометрическая прогрессия, первый член которой равен 2 и знаменатель равен 2.

Дают определение геометрической прогрессии.

Нужно в каждом случае найти n-й член

прогрессии.

Формулируют цель урока: вывести формулу n- члена геометрической прогрессии.

3

Освоение нового материала

Каждой группе предлагает одно и тоже задание:

1. найти второй, третий, четвертый, пятый члены геометрической прогрессии общего вида через взаимосвязь между соседними членами;

2. сделать замену b₁ и q;

3. вывести формулу n-го члена

Координирует работу групп, при необходимости даёт консультации. Предлагает проанализировать вывод формулы и сформулировать общий приём, используемый для вывода формулы, который будет широко применяться для решения биологических задач.

Работа по выводу формул происходит в группах по 4 человека;

Представитель одной из групп показывает вывод формулы на доске;

Используя формулу геометрической прогрессии, дают ответ на вопрос о количестве инфузорий после 15 размножения при идеальном условии выживания: b₁₅ = 2∙ 2¹⁴ = 32768.

4

Закрепление знаний учащихся

Краткий рассказ о способности размножения организмов (табл.2, табл.3)

Предлагает ответить на вопросы:

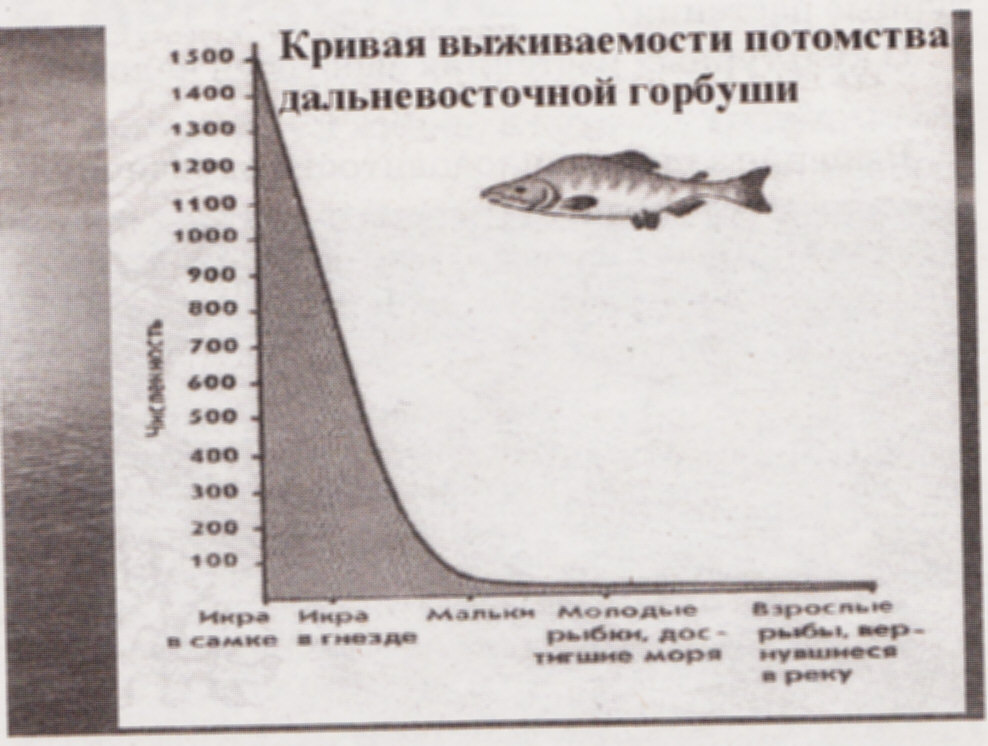
1. Почему не все особи выживают? Каковы, по вашему мнению причины, ограничивающие беспредельное размножение организмов? (табл.4)

2. Какое практическое значение имеет изучение интенсивности размножения?

3. Почему из всех птиц человек разводит преимущественно представителей отряда курообразных и гусеобразных? Известно. Что по качеству мяса, скорости роста, размерам, степени привыкания к человеку им не уступают ни дрофы, ни кулики, ни голуби. (табл. 5)

4. Почему сорняки более плодовиты?

Предлагает решить задачу о плодовитости одуванчика и некоторых видов рыб (Табл.6, табл. 7).

Предлагается индивидуальная работа. (выполнение теста с последующей проверкой) табл.8.

Слушают, делают необходимые записи.

Примерные ответы:

Влияние различных неблагоприятных условий, замедляющих рост и размножение микроорганизмов

Интенсивность размножений бактерий используют в пищевой промышленности, в фармацевтической, в сельском хозяйстве, в коммунальном хозяйстве и природоохранных мероприятиях. Огромное количество личинок и мух идёт на корм рыбам, в качестве добавок домашней птице, повышения урожая и т.д.

У данных представителей выше плодовитость.

О культурных растениях заботится человек

Делают расчёты в тетради, решают задачи.

Работают в тетради, затем сверяют свои ответы с ответами на слайде.

5

Подведение итогов. Рефлексия.

Задаёт вопросы:

1. Достигли ли цели урока?

2. Что нового узнали на уроке?

3. Где могут пригодиться полученные знания?

4. Над чем необходимо поработать дома?

Работа в группах, отвечают письменно на вопросы учителя.

По итогам рефлексии приходят к выводу, что для дальнейшей успешной работы им необходимо:

1. Знать формулу n-го члена геометрической прогрессии;

2. Применять формулу в процессе решения различных задач.

6

Домашнее задание

Предлагает домашнее задание на карточках.

Записывают домашнее задание и берут карточки.

Литература:

1. Бояркина Ю.А., Петрова З.В. Компетентностно-ориентированные задания по математике, ТОГИРРО, 2010,с.24-26

2. Журило Т, Кеверик Е. открытый урок // Математика, 2010. - №13.- с.30-32.

3. Сухова Т.С. Введение в биологию и зкологию: учебник для 5 класса общеобразовательной школы-М: Изд.»Вентана-Граф» 1997, с.49, 134.

Приложение №1

Таблица 1

Таблица 2.

Таблица №4

Таблица №5

Таблица №6Виды рыб

Количество икринок, откладываемых одной самкой

1

Треска

10 000 000

2

Обыкновенная щука

500 000

3

Лосось-кета

3 000

4

Тилапия

300

5

Кошачья акула

20

6

Катран

10

Таблица №7

Таблица № 8

Приложение №2

Тест

Выберите правильное утверждение.

1. Численность любого вида при отсутствии ограничений (обилие пищи, обилие мест обитания, отсутствия врагов и т.д.) растёт в соответствии…

А. С арифметической прогрессией.

Б. С прямой пропорциональной зависимостью.

В. С геометрической прогрессией.

Г. С обратной пропорциональной зависимостью.

2. Кривая роста численности (зависимость численности от времени) любого вида при отсутствии ограничений называется …

А. Гиперболой.

Б. Прямой.

В. Параболой.

Г. Экспонентой.

3. Бактерии способны очень быстро размножаться. Каждые полчаса из одной клетки появляются две. Если одну бактерию поместить в идеальные условия с обилием пищи, то за сутки её потомство должно составить 2⁴⁸ = 281 474 976 710 656 клеток. Такое количество бактерий занимает 0,25-литровый стакан. Подумайте, за какое время их количество удвоится и займёт пол-литровый объём. Выберите правильный ответ.

А. Одни сутки.

Б. Один час.

В. Двое суток.

Г. Полчаса

Приложение №3

Задание на дом

Задача. У капустной тли свой паразит - наездник афидиус, дающий за лето более 6 поколений по 30 особей (из них 50% самцов) в каждом.

а) Какого количества достигнет всё потомство от одного афадиуса через 6 месяцев, если этот паразит будет размножаться беспрепятственно?

б) Хватит ли к осени капустных тлей для питания такого количества афидиусов, если афидиус своё яйцо откладывают только в одну тлю?