Рабочая программа по алгебре для 11 класса общеобразовательной школы (профильный уровень)

Пояснительная записка

Рабочая программа по математике составлена на основе примерной программы по алгебре и началам анализа федерального компонента государственного стандарта среднего (полного) общего образования на профильном уровне, федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях, с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования, тематического планирования учебного материала, базисного учебного плана.

В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:

• развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;

• систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;

• развитие представлений о вероятностно-статистических закономерностях в окружающем мире;

• совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;

• формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.

Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:

• формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;

• овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;

• развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;

• воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.

Общеучебные умения, навыки и способы деятельности

В ходе изучения математики в профильном курсе старшей школы учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт:

проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;

решения широкого класса задач из различных разделов курса, поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;

планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использования и самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнения расчетов практического характера;

построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;

самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.

Место предмета в базисном учебном плане

Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе основного общего образования рабочая программа рассчитана на 170 учебных часов из расчета 5 учебных часов в неделю. Тематическое планирование составлено к УМК А.Г. Мордковича, П.В. Семенова. «Алгебра и начала анализа», 11 класс, М. «Мнемозина», 2012 год на основе федерального компонента государственного стандарта общего образования с учетом авторского тематического планирования учебного материала, приведенного в учебнике.

Учебно-тематический план по алгебре и математическому анализу

Класс: 11 класс (профильная группа)

Учитель: Лучинина Н.А.

Количество часов за год:

всего 170 часа;

в неделю 5 часов.

Плановых контрольных работ 10

Зачеты: 3

№

урока

Тема

Кол

час

Из них

Изучение нового и закрепление

Контроль

1-5

Повторение курса 10 класса.

5

4

1

Глава1. Многочлены.

16

14

2

6 - 10

Многочлены от одной переменной

5

11-14

Многочлены от нескольких переменных

4

15 - 19

Уравнения высших степеней

5

20 - 21

Контрольная работа №1

2

Глава 2.Степени и корни. Степенные функции

29

24

5

22- 23

Понятие корня n-ой степени из действительного числа.

2

24-27

Функции у =, их свойства и графики

4

28-31

Свойства корня п-й степени

4

32-36

Преобразование выражений, содержащих радикалы

5

37-38

Контрольная работа № 2

2

39-42

Понятие степени с любым рациональным показателем

4

43-47

Степенные функции. Их свойства и графики

5

48

Зачет

1

49-50

Контрольная работа №3

2

Глава 3. Показательная и логарифмическая функции

38

33

5

51-54

Показательная функция, ее свойства и график

4

55-58

Показательные уравнения

4

59-61

Показательные неравенства

3

62-63

Понятие логарифма

2

64-66

Логарифмическая функция, ее свойства и график

3

67-68

Контрольная работа № 4

2

69-73

Свойства логарифмов

5

74-78

Логарифмические уравнения

5

79-82

Логарифмические неравенства

4

83-85

Дифференцирование показательной и логарифмической функций

3

86

Зачет

1

87-88

Контрольная работа № 5

2

Глава 4. Первообразная и интеграл

11

10

1

89 - 92

Первообразная и неопределенный интеграл

4

93 - 98

Определенный интеграл

6

99

Контрольная работа № 6

1

Глава 5. Элементы теории вероятности и математической статистики

10

9

1

100-101

Вероятность и геометрия

2

102-105

Независимые повторения испытаний с двумя исходами

4

106-108

Статистические методы обработки информации

3

109

Контрольная работа № 7

1

Глава 6. Уравнения и неравенства. Системы уравнений и неравенств

40

35

5

110-113

Равносильность уравнений

4

114-117

Общие методы решения уравнений

4

118-120

Равносильность неравенств

3

121-124

Уравнения и неравенства с модулями

4

125-126

Контрольная работа № 8

2

127-130

Уравнения и неравенства со знаком радикала

4

131-133

Уравнения и неравенства с двумя переменными

3

134-135

Доказательство неравенств

2

136-141

Системы уравнений

6

142

Зачет

1

143-144

Контрольная работа № 9

2

145-149

Задачи с параметрами

5

Обобщающее повторение

21

17

4

150

Задачи на проценты

1

151

Чтение графиков функций

1

152

Решение простейших уравнений

1

153

Решение задач на анализ практической ситуации

1

154

Геометрический смысл производной

1

155

Исследование функции с помощью производной

1

156-157

Решение тригонометрических уравнений и систем

2

158-159

Логарифмические уравнения и неравенства

2

160-161

Показательные уравнения и неравенства

2

162-163

Уравнения и неравенства с параметром

2

164-165

Решение задач из теории целых чисел

2

166-169

Предаттестационная контрольная работа

4

170

Итоговый урок

1

Содержание тем учебного курса

Многочлены (16 часов)

Многочлены от одной переменной. Арифметические операции над многочленами от одной переменной. Делимость многочленов. Деление многочленов с остатком. Разложение многочлена на множители. Рациональные корни многочленов с целыми коэффициентами. Решение целых алгебраических уравнений. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Действия с многочленами. Однородная и симметрическая системы.

Формы контроля: Контрольная работа №1

Степени и корни. Степенные функции (29 часов).

Определение корня n-ой степени четной и нечетной степени.

Решение иррациональных уравнений. Свойства функции 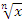при четном и нечетном значении n. Построение графиков функций, содержащих корень n-ой степени. . Свойства корня n-ой степени. Применение свойств корня n-ой степени при преобразовании иррациональных выражений. Определение степени с рациональным показателем. Преобразование выражений, содержащих степени с рациональным показателем. Свойства степенных функций в зависимости от показателя Вертикальные и горизонтальные асимптоты.

Формы контроля: Контрольная работа №2, №3, зачет.

Показательная и логарифмическая функции ( 38 часов).

Определение показательной функции. Свойства показательной функции в зависимости от основания. Решение показательных уравнений и неравенств, используя график. Методы и способы решения показательных уравнений. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.

Преобразования выражений, включающих арифметические операции, а также операции возведения в степень и логарифмирования.

Определение логарифмической функции. Зависимость свойств логарифмической функции от основания логарифма. Построение графиков логарифмической функции, решение логарифмических уравнений и неравенств с помощью графиков. Способы решения логарифмических уравнений. Способы решения логарифмических неравенств. Функция 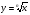, ее свойства, график, дифференцирование. Натуральные логарифмы. Формулы производных показательной и логарифмической функций.

Формы контроля: Контрольная работа №4, №5, зачет.

Первообразная и интеграл ( 11 часов ).

Определение первообразной. Правила отыскания первообразных. Неопределенный интеграл.. Первообразные элементарных функций. Правила вычисления первообразных.. Площадь криволинейной трапеции. Понятие об определенном интеграле. Формула Ньютона-Лейбница

Примеры применения интеграла в физике и геометрии.

Формы контроля: Контрольная работа №6, зачет.

Элементы комбинаторики, статистики и теории вероятностей (10 часов).

Табличное и графическое представление данных. Числовые характеристики рядов данных.

Геометрическая вероятность. Понятие о независимости событий. Независимые повторения испытаний с двумя исходами. Вероятность и статистическая частота наступления события. Статистические методы обработки информации. Гауссова кривая. Закон больших чисел.

Формы контроля: Контрольная работа №7.

Уравнения и неравенства. Системы уравнений и неравенств (40 часов).

Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных и тригонометрических уравнений и неравенств.

Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение систем уравнений с двумя неизвестными простейших типов. Решение систем неравенств с одной переменной.

Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел.

Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.

Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.

Определение уравнений с параметром. Примеры уравнений с параметром и способы их решения.

Формы контроля: Контрольная работа №8, №9, зачет.

Обобщающее повторение (20 часов)

Преобразование тригонометрических, логарифмических, выражений, выражений, содержащих степень. Решение всех видов уравнений, неравенств, систем уравнений и неравенств. Производная. Функции и графики. Выполение тестов.

Формы контроля: Итоговое тестирование .

Требования к уровню подготовки выпускников.

В результате изучения математики на профильном уровне в старшей школе ученик должен

Знать/понимать:

• значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

• значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;

• идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;

• значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;

• универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;

• различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;

• роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;

• вероятностных характер различных процессов и закономерностей окружающего мира.

Числовые и буквенные выражения

Уметь:

• выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;

• применять понятия, связанные с делимостью целых чисел, при решении математических задач;

• находить корни многочленов с одной переменной, раскладывать многочлены на множители;

• выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;

• проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.

Функции и графики

Уметь:

• определять значение функции по значению аргумента при различных способах задания функции;

• строить графики изученных функций, выполнять преобразования графиков;

• описывать по графику и по формуле поведение и свойства функций;

• решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.

Начала математического анализа

Уметь:

• находить сумму бесконечно убывающей геометрический прогрессии;

• вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;

• исследовать функции и строить их графики с помощью производной,;

• решать задачи с применением уравнения касательной к графику функции;

• решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;

• вычислять площадь криволинейной трапеции;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.

Уравнения и неравенства

Уметь:

• решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;

• доказывать несложные неравенства;

• решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;

• изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.

• находить приближенные решения уравнений и их систем, используя графический метод;

• решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• построения и исследования простейших математических моделей.

Элементы комбинаторики, статистики и теории вероятностей

Уметь:

• решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;

• вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для

• анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.

Литература

1. Настольная книга учителя математики. М.: ООО «Издательство АСТ»: ООО Издательство Астрель», 2004.

2. Тематическое приложение к вестнику образования. №4, 2012.

3. Требования к оснащению образовательного процесса в соответствии с содержательным наполнением учебных предметов федерального компонента государственного стандарта общего образования.

4. Мордкович А.Г. Алгебра и начала анализа. 11 кл.: В двух частях. Ч. 1: Учебник для общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, П.В. Семенов. - М.: Мнемозина, 2012.

5. Алгебра и начала анализа. 11 кл.: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений (профильный уровень) / А.Г. Мордкович, Л.О. Денищева, Л.И. Звавич, Т.А. Корешкова, Т.Н. Мишустина, А.Р. Рязановский, П.В. Семенов; под ред. А.Г. Мордковича. - М.: Мнемозина, 2012.

Дополнительная литература для ученика

1. Алгебра и начала анализа. Самостоятельные работы.11 класс. Л. А. Александрова. «Мнемозина», 2005 г.

2. Алгебра и начала анализа Контрольные работы. 11класс. Профильный уровень. В. И. Глизбург, «Мнемозина», 2008 г.

3. Алгебра и начала анализа. Тематические тесты и зачеты. 10-11классы. Л.О. Денищева, Т. А. Корешкова, «Мнемозина», 2005 г.

4. Самое полное издание типовых вариантов реальных заданий ЕГЭ 2013. Математика. Разработано Фипи, «АСТ -Астрель», 2013 г.

5. Математика, ЕГЭ 2013. Типовые тестовые задания. Разработано МИОО. Под редакцией А. Л. Семенова, И. В. Ященко. «Экзамен», 2013

Используемые ресурсы:

Цифровые: CD. Уроки алгебры Кирилла и Мефодия 10-11 классы, CD. Алгебра и начала анализа. 11 класс, CD. Готовимся к ЕГЭ. CD.Алгебра., Единый государственный экзамен. Математика. «Просвещение», 2009 г.

Интернет: , , , , , , , ,