- Учителю
- Урок по теме 'Смеси'
Урок по теме 'Смеси'
УРОК ПО ТЕМЕ : « РЕШЕНИЕ ЗАДАЧ НА СМЕСИ И СПЛАВЫ» 11 КЛАСС.
Цели урока: Рассмотреть основные общие приёмы решения задач на смеси и сплавы.
Вывести формулы для нахождения величин.
Научиться решать задачи с данным содержанием по основному уравнению и
по выведенным формулам.
Развивать умение применять полученные знания на практике.
Развивать интерес к математике.
Решить устно
-15 *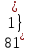 -19
-19 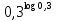 9-4
9-4 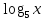 +
+ 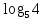 =
= 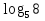
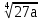 *
* 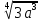
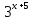 =81 3
=81 3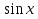 +3
+3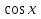
У=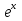 +6
+6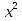
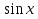 =1\2
=1\2
Объяснение новой темы
При решении задач на смеси и сплавы необходимо составить уравнение вида:
mp + mp =(m+m)p ,
где m- масса вещества, р - процентное содержание вещества в сплаве или смеси.
Задание: выведите из формулы основные характеристики: m , m , p , p ,p.
Запишите полученные формулы на доске.
Задача 1
Даны два куска с различным содержанием олова.
1 кусок массой 300г содержит 20% олова, а второй 200г содержит 40% олова.
Сколько % олова будет содержать сплав из этих кусков?
( решаю у доски с пояснением)
Задача 2 ( решают самостоятельно)
Имеется 2 куска сплава олова и свинца. 1 кусок массой 300г содержит 60% олова, а 2-ой содержит 40%. Сколько граммов от второго куска надо добавить к первому , чтобы получить сплав с содержанием 56% олова.
Задача 3 Сборник заданий ЕГЭ 2008г
№ 518 Из сосуда, полностью заполненного 12% раствором соли, отлили 1л и налили 1л воды. После этого в сосуде оказался 9% раствор соли. Сколько литров вмещает сосуд?
(решаем у доски с пояснением)
№511 ( самостоятельно) Объясняю запись уравнения.
Сколько миллилитров воды нужно добавить к 500 мл. 96% -ного раствора спирта, чтобы получить 40% -ный раствор спирта?
( проверка решения у доски)
Задача 4 ( историческая)
У одного человека были для продажи вина двух сортов, первое 10 гривен за ведро, второе 6, захотелось ему сделать из этих вин третье вино, чтобы ему цена была по 7 гривен. Какие части надлежит взять из тех вин для наполнения ведра третьего вина.
( 1 гривна-10 коп)
Самостоятельно : Имеются 2 куска сплава, содержащие 40% и 60% олова. В каком отношении ( по массе) нужно сплавить части этих кусков , чтобы получить сплав с 45% содержанием олова.
Домашнее задание.
Сборник заданий ЕГЭ 2006
№ 1027 Смешали 30% раствор соляной кислоты с 10% и получили 600г 15% раствора.
Сколько грамм 10% раствора было взято.
№ 1021 Два спиртовых раствора борной кислоты одинаковой массы слили в один сосуд. Скольки процентный раствор получили в результате, если первый раствор 5% , а второй 1%.
Итог урока.
Задача 1
Даны два куска с различным содержанием олова.
1 кусок массой 300г содержит 20% олова, а второй 200г содержит 40% олова.
Сколько % олова будет содержать сплав из этих кусков?
Задача 2
Имеется 2 куска сплава олова и свинца. 1 кусок массой 300г содержит 60% олова, а 2-ой содержит 40%. Сколько граммов от второго куска надо добавить к первому , чтобы получить сплав с содержанием 56% олова.
Задача 3 Сборник заданий ЕГЭ 2008г
№ 518 Из сосуда, полностью заполненного 12% раствором соли, отлили 1л и налили 1л воды. После этого в сосуде оказался 9% раствор соли. Сколько литров вмещает сосуд?
№511 ( самостоятельно) Объясняю запись уравнения.
Сколько миллилитров воды нужно добавить к 500 мл. 96% -ного раствора спирта, чтобы получить 40% -ный раствор спирта?
Задача 4 ( историческая)
У одного человека были для продажи вина двух сортов, первое 10 гривен за ведро, второе 6, захотелось ему сделать из этих вин третье вино, чтобы ему цена была по 7 гривен. Какие части надлежит взять из тех вин для наполнения ведра третьего вина.
( 1 гривна-10 коп)
Самостоятельно : Имеются 2 куска сплава, содержащие 40% и 60% олова. В каком отношении ( по массе) нужно сплавить части этих кусков , чтобы получить сплав с 45% содержанием олова.
Домашнее задание.
Сборник заданий ЕГЭ 2006
№ 1027 Смешали 30% раствор соляной кислоты с 10% и получили 600г 15% раствора.
Сколько грамм 10% раствора было взято.
№ 1021 Два спиртовых раствора борной кислоты одинаковой массы слили в один сосуд. Скольки процентный раствор получили в результате, если первый раствор 5% , а второй
1%.